Nonlinear Control of Bioprocess Using Feedback Linearization, Backstepping, and Luenberger Observers ()
1. Introduction
In process control, a major difficulty is to provide direct real-time measurements of the state variables required to implement advanced monitoring and control methods on bioreactors [1] -[5] . Dissolved oxygen concentration in bioreactors, temperature in non-isothermal reactors and gaseous flow rates, are available for on-line measurement while the values of concentration of products, reactants and/or biomass are often available only via on-line analysis [2] - [4] , which means that these variables are not available for real-time feedback control. An alternative is to use state observers which, in conjunction with the process model and available measurements, can generate accurate estimates of the unmeasured and/or inaccessible states effectively. Exponential and asym- ptotic observers and their variants to estimate unmeasured states in bioprocess systems have appeared in [1] - [5] . In [6] , Dochain and Perrier applied backstepping [7] - [9] , techniques to the nonlinear control of microbial growth problem in a CSTR (continuously stirred tank reactor) and two controllers were proposed. The first one was a non-adaptive version, while the second one was an adaptive version in which the maximum specific growth rate was estimated on-line. However, backstepping-based observer design was not considered in [6] .
In this paper, a complete development of observer-based control is presented that includes feedback linearization [7] [8] [10] [11] , backstepping [7] - [9] , Luenberger observer [12] with feedback linearization, and Luenberger observer with backstepping.
The paper is organized as follows. Section 2 presents the bioprocess model for control design. Theoretical foundation of input-output feedback linearization (FBL) and controller design are outlined in Section 3 with simulation results. Section 4 addresses the formulation and application of backstepping (BS) control with simulation results. In Section 5, simulation results are compared for both approaches, i.e., FBL and BS. Section 6 addresses the design of Luenberger observers for FBL and BS controls with simulations. The conclusions are presented in Section 7.
2. Bioprocess Model
The model dynamics in a CSTR (continuous stirred tank reactor) with a simple microbial growth reaction, with one substrate 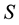 and biomass
and biomass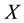 , are given by the following equations [1] :
, are given by the following equations [1] :
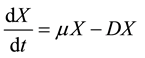 , (1)
, (1)
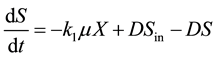 , (2)
, (2)
where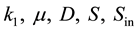 , represent the yield coefficient, specific growth rate (h−1), dilution rate (h−1), and substrate concentration (grams/lit) in the influent and reactor, respectively.
, represent the yield coefficient, specific growth rate (h−1), dilution rate (h−1), and substrate concentration (grams/lit) in the influent and reactor, respectively.
The biomass concentration 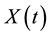 (grams/lit) is the variable which is to be controlled. Defining the parameter
(grams/lit) is the variable which is to be controlled. Defining the parameter  as
as 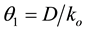 and expressing specific growth rate
and expressing specific growth rate 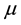 as
as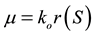 , the dynamical Equations (1) and (2) above can be written as [6]
, the dynamical Equations (1) and (2) above can be written as [6]
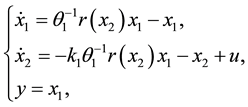 (3)
(3)
where it is assumed that the biomass concentration 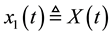 can be measured with a sensor, i.e., the output is given by
can be measured with a sensor, i.e., the output is given by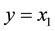 , while
, while 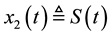 denotes the substrate concentration and
denotes the substrate concentration and 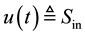 is the control input. The bioprocess model given by (3) can be written compactly in an alternate state-space form as:
is the control input. The bioprocess model given by (3) can be written compactly in an alternate state-space form as:
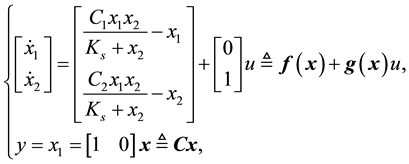 (4)
(4)
where ![]() and
and![]() . Note that in (4),
. Note that in (4), ![]() has been written using “Monod form” for reac-
has been written using “Monod form” for reac-
tion kinetics, which can expressed as
![]() , (5)
, (5)
![]() . (6)
. (6)
We will use (3) for back stepping control and observer design and (4) will be utilized for developing the control law and observer design using the feedback linearization approach. Typical values of the model parameters needed for the simulation studies are given in Table 1 [6] .
3. Feedback Linearization (FBL) Control Design
The main intent of this section is to investigate control design using the input-output feedback linearization (FBL) technique. Consider a general nonlinear control-affine SISO system described by [7] [8] [10] [11] ,
![]() , (7)
, (7)
![]() , (8)
, (8)
where ![]() is the state vector,
is the state vector, ![]() are the control and output signals, respectively;
are the control and output signals, respectively; ![]() is a smooth function, and
is a smooth function, and ![]() are smooth vector fields on D, where D is an open set. Given the nonlinear system (7) and the measurement (8), our goal is to find a diffeomorphism or nonlinear transformation of the form
are smooth vector fields on D, where D is an open set. Given the nonlinear system (7) and the measurement (8), our goal is to find a diffeomorphism or nonlinear transformation of the form![]() ,
, ![]() with
with ![]() that transforms the nonlinear system in the
that transforms the nonlinear system in the ![]() -coordinates to a linear system in the
-coordinates to a linear system in the ![]() -coordinates. Differentiating the output
-coordinates. Differentiating the output ![]() with respect to t yields
with respect to t yields
![]() , (9)
, (9)
where ![]() and
and ![]() denote the Lie derivatives of
denote the Lie derivatives of ![]() with respect to
with respect to ![]() and
and
![]() , respectively. If
, respectively. If![]() , then
, then ![]() is independent of
is independent of![]() . Continuing successive differentiation
. Continuing successive differentiation ![]() times until
times until ![]() appears explicitly, we obtain
appears explicitly, we obtain
![]() , (10)
, (10)
where ![]() is a nonlinearity cancellation factor and
is a nonlinearity cancellation factor and ![]() is a scalar function. The smallest integer
is a scalar function. The smallest integer ![]() for which
for which ![]() appears is referred to as the relative degree, i.e., when
appears is referred to as the relative degree, i.e., when![]() . The nonlinear system (7) - (8) is said to have a well-defined relative degree
. The nonlinear system (7) - (8) is said to have a well-defined relative degree ![]() in a region
in a region ![]() if
if
![]() (11)
(11)
for all![]() . Note that
. Note that![]() . From (10), define
. From (10), define
![]() , (12)
, (12)
where ![]() is a one-dimensional transformed input created by the feedback linearization process. Equation (12) yields the linearizing feedback control law [7] [8] [10] [11] :
is a one-dimensional transformed input created by the feedback linearization process. Equation (12) yields the linearizing feedback control law [7] [8] [10] [11] :
![]() , (13)
, (13)
provided ![]() is invertible. If
is invertible. If![]() , then
, then
![]() (14)
(14)
If ρ < n, the diffeomorphism Tfbl(x) comprises of both external and internal dynamics, i.e., ![]() , where
, where ![]() represents the external dynamics state vector and
represents the external dynamics state vector and ![]() the internal dynamics state vector, respectively; furthermore, the differential equation for
the internal dynamics state vector, respectively; furthermore, the differential equation for ![]() is linear, while that for
is linear, while that for ![]() is typically nonlinear. For the bioprocess model given by (4),
is typically nonlinear. For the bioprocess model given by (4), ![]() , so the system is fully linearizable. We obtain, from (4), (12) and (14),
, so the system is fully linearizable. We obtain, from (4), (12) and (14),
![]() (15)
(15)
![]() , (16)
, (16)
![]() , (17)
, (17)
where ![]() is a local diffeomorphism for the system. Using (17) with (12) for
is a local diffeomorphism for the system. Using (17) with (12) for![]() , the original nonlinear system described by (3) and (4) is transformed into a linear system of the form
, the original nonlinear system described by (3) and (4) is transformed into a linear system of the form
![]() (18)
(18)
where
![]() (19)
(19)
and ![]() and
and ![]() are, respectively, controllable and observable pairs. A suitable tracking control law for the transformed input
are, respectively, controllable and observable pairs. A suitable tracking control law for the transformed input ![]() in the linear system (18) for
in the linear system (18) for ![]() can be formulated as, with (17),
can be formulated as, with (17),
![]() , (20)
, (20)
where![]() ,
, ![]() is a bounded reference with bounded derivatives
is a bounded reference with bounded derivatives ![]() and
and![]() ,
, ![]() ,
,
and the constant feedback gain matrix ![]() is determined such that
is determined such that ![]() is Hurwitz. Furthermore, the gain matrix
is Hurwitz. Furthermore, the gain matrix ![]() can be determined by various design methods, such as pole placement (PP) and linear quadratic regulator (LQR). We shall focus on the PP design in this paper. Substituting (20) into (18) yields the closed-loop system
can be determined by various design methods, such as pole placement (PP) and linear quadratic regulator (LQR). We shall focus on the PP design in this paper. Substituting (20) into (18) yields the closed-loop system
![]() (21)
(21)
The linearizing feedback control law in the ![]() -domain can be written by setting
-domain can be written by setting ![]() in (13) as
in (13) as
![]() , (22)
, (22)
which yields the closed-loop system
![]() (23)
(23)
The design of a PP control law (20) for the 2nd-order system (18) is achieved by choosing a damping ratio ![]() that prohibits overshoot, and an undamped natural frequency
that prohibits overshoot, and an undamped natural frequency ![]() (rad/sec). The resulting closed-
(rad/sec). The resulting closed-
loop poles are given by ![]() where
where ![]() and the resulting gain
and the resulting gain
![]() is computed with Matlab’s ACKER command. Simulation studies for the closed-loop system with FBL control were conducted using (23). The controller performance was evaluated for a square-wave set-point reference
is computed with Matlab’s ACKER command. Simulation studies for the closed-loop system with FBL control were conducted using (23). The controller performance was evaluated for a square-wave set-point reference ![]() that alternates every 20 hours between 3 grams/lit and 4 grams/lit as shown in Figure 1 (dotted line). The initial conditions were chosen as
that alternates every 20 hours between 3 grams/lit and 4 grams/lit as shown in Figure 1 (dotted line). The initial conditions were chosen as ![]() and
and ![]() [6] . The simulation results are depicted in Figure 1 which shows that the responses are satisfactory.
[6] . The simulation results are depicted in Figure 1 which shows that the responses are satisfactory.
4. Backstepping (BS) Control Design
We shall address the design of back stepping (BS) [7] -[9] control in this section, where the parameter ![]() is assumed known. The objective here is to design a BS control law
is assumed known. The objective here is to design a BS control law ![]() such that the output
such that the output ![]() tracks the reference
tracks the reference![]() . We will also compare the performance of the closed-loop bioprocess under FBL control
. We will also compare the performance of the closed-loop bioprocess under FBL control ![]() given by (22) and the BS control
given by (22) and the BS control ![]() to be developed below. The formulation presented here considers a general bounded differentiable reference signal
to be developed below. The formulation presented here considers a general bounded differentiable reference signal ![]() instead of the constant set-point regulation in [6] . Consider the nonlinear system in the form of (3) reproduced below for ease of reference:
instead of the constant set-point regulation in [6] . Consider the nonlinear system in the form of (3) reproduced below for ease of reference:
![]() (3)
(3)
where ![]() is a known constant parameter. We treat
is a known constant parameter. We treat ![]() as the virtual control of the first subsystem
as the virtual control of the first subsystem![]() in (3) and let
in (3) and let ![]() be the stabilizing function such that
be the stabilizing function such that ![]() racks
racks![]() . Define the tracking errors as
. Define the tracking errors as
![]() (24)
(24)
![]() , (25)
, (25)
![]()
Figure 1. Responses of closed-loop bioprocess (23) under FBL control ![]() with PP design.
with PP design.
where ![]() is the error between
is the error between ![]() and
and![]() . Taking the derivative of
. Taking the derivative of ![]() yields, with (25),
yields, with (25),
![]() . (26)
. (26)
Consider the Lyapunov function candidate
![]() , (27)
, (27)
which yields the derivative, with (26),
![]() . (28)
. (28)
Choosing the stabilizing function ![]() to make
to make ![]() in (28) yields
in (28) yields
![]() . (29)
. (29)
Substituting (29) into (26) and (28) yields, respectively,
![]() , (30)
, (30)
![]() (31)
(31)
From (31), if![]() , then
, then ![]()
![]() and the origin
and the origin ![]() is globally asymptotically stable, whereby achieving global tracking with
is globally asymptotically stable, whereby achieving global tracking with![]() . The term
. The term ![]() will be addressed in the next step.
will be addressed in the next step.
The next step is to develop a BS control law for![]() . The derivative of
. The derivative of ![]() given by (25) satisfies, with (3) and (29),
given by (25) satisfies, with (3) and (29),
![]() , (32)
, (32)
![]() , (33)
, (33)
where
![]() , (34)
, (34)
and ![]() is given by (6).
is given by (6).
To stabilize the ![]() -system the Lyapunov function candidate as
-system the Lyapunov function candidate as
![]() . (35)
. (35)
The derivative of ![]() is given by, with (31) and (33),
is given by, with (31) and (33),
![]() . (36)
. (36)
Defining ![]() to be the BS control, and choosing
to be the BS control, and choosing ![]() to make the term
to make the term ![]() in (36) yields
in (36) yields
![]() . (37)
. (37)
Substituting (37) into (33) and (36), we obtain,
![]() (38)
(38)
![]() . (39)
. (39)
Since ![]() for all
for all![]() , it follows that
, it follows that ![]() is globally asymptotically stable. Additionally, the stability result can also be established by combing the error equations from (30) and (38) as
is globally asymptotically stable. Additionally, the stability result can also be established by combing the error equations from (30) and (38) as
![]() . (40)
. (40)
Since ![]() is a skew-symmetric Hurwitz matrix for all
is a skew-symmetric Hurwitz matrix for all ![]() and
and![]() , it follows that the equilibrium
, it follows that the equilibrium ![]() is globally asymptotically stable. Moreover,
is globally asymptotically stable. Moreover, ![]() is an observable pair, where
is an observable pair, where ![]() (see (53)). Since (40) is in the form of a standard linear time-invariant (LTI) system, a Luenberger observer [12] for state estimation can be constructed for the system, and will be investigated in Section 6.
(see (53)). Since (40) is in the form of a standard linear time-invariant (LTI) system, a Luenberger observer [12] for state estimation can be constructed for the system, and will be investigated in Section 6.
Meanwhile, the closed-loop bioprocess under BS control is given by,
![]() (41)
(41)
where ![]() is given by (37).
is given by (37).
Simulation studies were conducted using (41) with the backstepping gains![]() . The reference signal
. The reference signal ![]() and the initial condition
and the initial condition ![]() were same as those used for the FBL control in Section 3. The simulation is depicted in Figure 2 which shows that the responses were satisfactory.
were same as those used for the FBL control in Section 3. The simulation is depicted in Figure 2 which shows that the responses were satisfactory.
5. Comparison of FBL and BS Designs
The simulation results for the FBL versus BS designs using the gains reported in Sections 3 and 4 are shown in Figure 3 and Figure 4 for comparison purposes.
It can be seen that both ![]() and
and ![]() asymptotically with no overshoot. It can also be seen that the magnitudes of
asymptotically with no overshoot. It can also be seen that the magnitudes of ![]() are slightly larger than those of
are slightly larger than those of![]() . However, the reverse can also be obtained by tuning
. However, the reverse can also be obtained by tuning ![]() and
and![]() .
.
6. Observer-Based FBL and BS Controls
As mentioned before that not all state variables are measured in the bioreactor systems; therefore, suitable observers are needed for realizing the full-state feedback control designs proposed in Sections 3 and 4. We shall
![]()
Figure 2. Responses of closed-loop bioprocess (41) under BS control ![]() for
for![]() .
.
![]()
Figure 3. Comparing FBL responses in Figure 1 and BS responses in Figure 2.
investigate the constructions of Luenberger observers for the FBL-based and BS-based control approaches in this section
6.1. Luenberger Observer for FBL Control
Since only ![]() is measured in (4), a Luenberger observer [12] can be constructed for full-state estimation needed for full-state control of the bioprocess system. Using (21), a full-state observer can be constructed as
is measured in (4), a Luenberger observer [12] can be constructed for full-state estimation needed for full-state control of the bioprocess system. Using (21), a full-state observer can be constructed as
![]() (42)
(42)
where ![]() is the observer system matrix and
is the observer system matrix and ![]() the observer gain matrix to be determined such that
the observer gain matrix to be determined such that ![]() is Hurwitz, provided that
is Hurwitz, provided that ![]() is an observable pair (which is the case in the present problem). The gain matrix L in (42) can be computed using a Luenberger observer [12] with pole placement (PP) and/or Kalman-Bucy filter [13] design techniques. We shall focus on the PP design method; henceforth L and
is an observable pair (which is the case in the present problem). The gain matrix L in (42) can be computed using a Luenberger observer [12] with pole placement (PP) and/or Kalman-Bucy filter [13] design techniques. We shall focus on the PP design method; henceforth L and ![]() in (42) will be denoted by
in (42) will be denoted by ![]() and
and![]() , respectively. It should be noted that for a general LTI system characterized by
, respectively. It should be noted that for a general LTI system characterized by![]() , where
, where ![]() is an
is an
observable pair, the pair ![]() may not be observable, because full-state feedback can destroy ob-
may not be observable, because full-state feedback can destroy ob-
servability; furthermore, ![]() may be unstable even though
may be unstable even though ![]() is designed to be stable [14] [15] .
is designed to be stable [14] [15] .
Now using (21) and (42), it can readily be shown that the estimation error ![]() satisfies,
satisfies,
![]() , (43)
, (43)
where the initial condition ![]() is arbitrary. Since
is arbitrary. Since ![]() is Hurwitz, it follows that
is Hurwitz, it follows that
![]() (44)
(44)
for all![]() .
.
Using the transformation defined by (17), the observer described by (42) in the ![]() -coordinates can be transformed back to the
-coordinates can be transformed back to the ![]() -coordinates as
-coordinates as
![]() , (45)
, (45)
where ![]() and
and ![]() is the Jacobian matrix associated with (17) given by
is the Jacobian matrix associated with (17) given by
![]() . (46)
. (46)
In summary, the observer-based control system with feedback linearization for the bioprocess under consideration has the form
![]() (47)
(47)
![]() , (48)
, (48)
where ![]() is the initial estimate of
is the initial estimate of ![]() and
and
![]() , (49)
, (49)
![]() , (50)
, (50)
![]() , (51)
, (51)
![]() (52)
(52)
6.2. Luenberger Observer for BS Control
In this section we pursue our final objective, i.e., to design a Luenberger observer based on the BS formulation using the error Equation (40). To construct an observer for (40), we need an output equation which can be defined as,
![]() , (53)
, (53)
where ![]() is known and
is known and ![]() is an observable pair.
is an observable pair.
We present the following proposition.
Proposition 1
Consider the bioprocess system described by (3) and (4). A Luenberger observer for the associated error system (40) with measurement given by (53) can be constructed as
![]() (54)
(54)
where ![]() and
and ![]() is the observer gain matrix to be determined by, for example poleplace- ment, such that the observer matrix
is the observer gain matrix to be determined by, for example poleplace- ment, such that the observer matrix ![]() is Hurwitz. Since
is Hurwitz. Since ![]() is already Hurwitz and
is already Hurwitz and ![]() is an observable pair,
is an observable pair, ![]() can be determined such that the real parts of the eigenvalues of
can be determined such that the real parts of the eigenvalues of ![]() lie on the left-side of those of
lie on the left-side of those of ![]() on the open left-half plane, if desirable. Furthermore, (54) can be expressed in the x-coordinates as
on the open left-half plane, if desirable. Furthermore, (54) can be expressed in the x-coordinates as
![]() (55)
(55)
Proof: First, we need to show that the estimate ![]() converges to its true value
converges to its true value![]() . Define the estimation error as
. Define the estimation error as![]() . From (40) and (54), it follows that
. From (40) and (54), it follows that ![]() satisfies,
satisfies,
![]() (56)
(56)
where ![]() is the initial condition. Since
is the initial condition. Since ![]() is Hurwitz, it follows that
is Hurwitz, it follows that
![]() , (57)
, (57)
for arbitrary ![]() Next, using, (24), (25) and (29), the coordinates transformation for the error-system can be obtained as
Next, using, (24), (25) and (29), the coordinates transformation for the error-system can be obtained as
![]() . (58)
. (58)
Equation (58) yields the Jacobian matrix
![]() , (59)
, (59)
where ![]() is nonsingular for
is nonsingular for ![]() so that
so that ![]() is a local diffeomorphism for (3). Equa-
is a local diffeomorphism for (3). Equa-
tions (58) and (59) yield ![]() and, from (53) and (54),
and, from (53) and (54),
![]() , (60)
, (60)
where ![]() is the inverse of
is the inverse of![]() , and
, and
![]() , (61)
, (61)
![]() (62)
(62)
which complete the proof. ![]()
The observer design technique developed here is interesting and attractive and is different from the two-filter approach in [9] . The technique can be applied to a wide class of BS-based error systems.
In summary, the observer-based control system with the BS formulation for the bioprocess is described by
![]() , (63)
, (63)
![]() (64)
(64)
where ![]() is the initial estimate of
is the initial estimate of![]() .
.
Simulation studies for the proposed observer-based FBL and BS controls were conducted and compared. The initial conditions were chosen as ![]() and
and![]() . The set-point reference
. The set-point reference ![]() was the same as before. The model parameters were given in Table 1 and Table 2.
was the same as before. The model parameters were given in Table 1 and Table 2.
In Figure 5, results for observer-based FBL control scheme described by (47) and (48) are shown. It can be seen that the estimates ![]() and
and ![]() converged to the true states around
converged to the true states around ![]() h. In Figure 6, results for the observer-based BS control scheme are presented. Convergence of the estimated states to the actual states can also be seen from this figure, and are similar to those presented in Figure 2.
h. In Figure 6, results for the observer-based BS control scheme are presented. Convergence of the estimated states to the actual states can also be seen from this figure, and are similar to those presented in Figure 2.
In Figure 7, the behavior of the error variables ![]() and
and ![]() defined by (24) and (25) which satisfy (40) in the backstepping scheme is shown. It is evident that
defined by (24) and (25) which satisfy (40) in the backstepping scheme is shown. It is evident that ![]() and
and ![]() smoothly after the transients are over around
smoothly after the transients are over around ![]() h.
h.
7. Conclusion
Observers are critical to control system analysis and designs that employ full-state feedback, where not all the state variables are accessible for on-line, real-time measurements, and/or where the measurements are corrupted by noise. Indeed, the design of suitable linear or nonlinear observers or filters leading to observer-based control technology is an integral part of real world control system applications. In this paper, observer-based control strategies were developed for a nonlinear bioprocess system using feedback linearization and backstepping control techniques; in particular, a Luenberger observer for backstepping control was formulated using the error equation resulted from the backstepping design procedure. The observer design technique developed here is interesting and attractive and is different from the two-filter approach known in the literature. Simulation results with and without observers for both the FBL and BS schemes are presented and compared. The results were excellent and demonstrated the feasibility and effectiveness of the proposed approaches.
![]()
Table 2. Controllers and observer gains.
![]()
Figure 5. Responses of observer-based FBL control scheme (47) and (48): ![]() and
and ![]() smoothly.
smoothly.
![]()
Figure 6. Responses of observer-based BS control scheme (63) and (64): ![]() and
and ![]() smoothly.
smoothly.
![]()
Figure 7. Evolution of the backstepping error variables: ![]() and
and ![]() smoothly.
smoothly.
Acknowledgements
The authors would like to thank all the reviewers for their feedbacks and constructive criticisms.