1. Introduction
This paper proposes a novel discrete differential geometry of n-simplices, which is originally developed for protein structure analysis [1] [2] . Discrete differential geometry is the study of discrete equivalents of the geometric notions and methods of classical differential geometry [3] [4] . It mainly deals with polygonal curves and polyhedral surfaces whose properties are analogous to continuous counterparts, where the smooth theory is established as limit of the discrete theory.
On the other hand, we consider connection between space-filling n-simplices. We define gradient of n-simplices and obtain a flow of n-simplices by piling up n-cubes diagonally. Second derivative along a trajectory is given as a binary-valued sequence for any n (>1). As a result, we could encode the shape of n-dimensional objects if we approximate them by sweeping the occupied area with a trajectory of n-simplices.
Proteins are a sequence of amino acids linked by peptide bonds and fold into a unique three-dimensional structure in nature. Protein backbone structure is usually studied via manually-curated hierarchical classification [5] [6] but there also exist studies on differential geometric approach for protein structure analysis [7] -[11] . As for discrete differential geometry of protein backbones, proteins are usually represented as a polygonal chain, where curvature and torsion are defined at each vertex [7] .
In our method, protein backbone structures are approximated by a trajectory of 3-simplices (tetrahedrons). Particularly we consider second derivative along a trajectory to encode local protein structures. Our method performs comparably with more sophisticated but more time-consuming methods which are specifically designed for protein structure analysis [12] [13] . In the following, we first describe the discrete differential geometry of n-simplices. Then, we apply the mathematical framework to analysis of protein structures and propose a simple encoding method which translates the conformation of a protein backbone into a 16-valued sequence.
2. Discrete Differential Geometry of n-Simplices
2.1. Basic Ideas
Recall that an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. As an introduction, we would consider the case of n = 2 before we give the definitions in the general case. In the case of n = 2, we obtain a flow of 2-simplices (triangles) by piling up unit cubes in the three-dimensional Euclidean space  as shown in Figure 1(a).
as shown in Figure 1(a).
First, cubes are pilled up in the direction of , where three upper faces of each unit cube are divided into two triangles by a diagonal line. Then, the diagonal lines on the faces of the cubes form a drawing on the surface of the “peaks and valleys” of cubes. By projecting the drawing onto a hyperplane that is perpendicular to
, where three upper faces of each unit cube are divided into two triangles by a diagonal line. Then, the diagonal lines on the faces of the cubes form a drawing on the surface of the “peaks and valleys” of cubes. By projecting the drawing onto a hyperplane that is perpendicular to , a flow of triangles would be obtained. For example, the grey “slant” triangles on the surface specify the closed trajectory of the grey “flat” triangles on the hyperplane in Figure 1(a).
, a flow of triangles would be obtained. For example, the grey “slant” triangles on the surface specify the closed trajectory of the grey “flat” triangles on the hyperplane in Figure 1(a).
2.2. Differential Structure
Because of convenience, we use monomials to represent coordinates of points. That is, point  is denoted by monomial
is denoted by monomial  of n indeterminates for integer n (n > 1).
of n indeterminates for integer n (n > 1).
First of all, we give the definition of “slant” and “flat” n-simplices. Let’s consider n-cube in the n-dimensional Euclidean space . Note that the facets of n-cubes are
. Note that the facets of n-cubes are  -dimensional unit cubes. To obtain “slant” n-simplices, we divide each of the n facets which contain origin
-dimensional unit cubes. To obtain “slant” n-simplices, we divide each of the n facets which contain origin  into
into 
 -simplices along diagonal as follows.
-simplices along diagonal as follows.
Definition 1. For any integer n > 1, n-dimensional standard lattice  is the collection of all integer points of
is the collection of all integer points of , i.e.,
, i.e.,
 .
.
Definition 2. For any integer n > 1, the collection 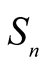 of all slant n-simplices is defined by
of all slant n-simplices is defined by
 where
where  is the n-th symmetric group and
is the n-th symmetric group and  denotes the convex hull of n points
denotes the convex hull of n points
 i.e.,
i.e.,
 .
.

Figure 1. Discrete differential geometry of 2-simplices: (a) “Peaks and valleys” of cubes; (b) Tangent bundle-like structure; (c) Local trajectory; (d) Smoothness condition.
Definition 3. For any integer n > 1, the collection  of all flat n-simplices is defined as the quotient of
of all flat n-simplices is defined as the quotient of  by “shift operator”
by “shift operator”  on
on , i.e,
, i.e,
 where
where .
.
Definition 4. Tangent bundle-like structure  is defined on
is defined on  as the quotient of
as the quotient of  by
by , i.e.,
, i.e.,

For example, triangle  specifies element
specifies element  of
of  over element
over element  of
of  (Figure 1(b)).
(Figure 1(b)).
Definition 5. Gradient  of
of  is defined as a monomial of degree n − 1, i.e.,
is defined as a monomial of degree n − 1, i.e.,
 .
.
For simplicity, we occasionally denote  by
by , where
, where . That is
. That is .
.
Note that we could identify  with
with  by one-to-one correspondence
by one-to-one correspondence
 .
.
A gradient over a flat n-simplex specifies a local trajectory at the flat n-simplex as follows.
Definition 6. The local trajectory specified by , where
, where , is a collection of three adjacent flat n-simplices
, is a collection of three adjacent flat n-simplices
 where
where  and
and .
.
For example,  specifies local trajectory
specifies local trajectory  at
at  (Figure 1(c)). We would obtain a flow on
(Figure 1(c)). We would obtain a flow on  by patching these local trajectories together.
by patching these local trajectories together.
To define the “second derivative” along a trajectory, we would impose a kind of “smoothness condition” on local trajectories.
Definition 7. (Smoothness condition). Let 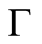 be a section of
be a section of  on
on 
where . Suppose that
. Suppose that . Then, we impose the following conditions on the local trajectory:
. Then, we impose the following conditions on the local trajectory:

Remark 8. For any two consecutive n-simplices  on a trajectory, there exist
on a trajectory, there exist  and
and 
s.t.  and
and . Monomial
. Monomial  is uniquely determined by
is uniquely determined by  and is included in both
and is included in both  and
and  for any section
for any section  of
of  on
on . That is,
. That is,  corresponds to the contact surface between two consecutive slant n-simplices.
corresponds to the contact surface between two consecutive slant n-simplices.
As an example, let’s consider the case of n = 2 shown in Figure 1(d), where the gradient at current triangle  is
is . Then, the gradient at next triangle
. Then, the gradient at next triangle  could assume either
could assume either  or
or . Otherwise, we couldn’t connect the two consecutive slant triangles over the trajectory “smoothly” as shown in the figure.
. Otherwise, we couldn’t connect the two consecutive slant triangles over the trajectory “smoothly” as shown in the figure.
2.3. Tangent Cone and Section of TBn
Now we give the definition of the “peaks and valleys” of n-simplices (Figure 1(a)).
Definition 9. For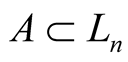 , tangent cone
, tangent cone  of
of  is defined as follows:
is defined as follows:
 .
.
Definition 10. For tangent cone 
 , boundary surfaces
, boundary surfaces  is defined by
is defined by
 where
where  and, for
and, for ,
,
 .
.
Then, 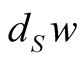 specifies a unique slant n-simplex over each
specifies a unique slant n-simplex over each  and we obtain a section of
and we obtain a section of  on
on .
.
Definition 11.  is the section of
is the section of  on
on  induced by tangent cone
induced by tangent cone , i.e., for
, i.e., for ,
,
 .
.
Note that tangent cone  induces a section of
induces a section of  on
on  by
by . Patching the local trajectories specified by
. Patching the local trajectories specified by  together, we would obtain a flow on
together, we would obtain a flow on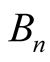 . As an example, let’s consider the “peaks and valleys” shown in Figure 1(a), which is induced by
. As an example, let’s consider the “peaks and valleys” shown in Figure 1(a), which is induced by .
.
Let’s start from triangle  (grey) and move downward (Figure 2):
(grey) and move downward (Figure 2):  and
and
 .
.  specifies local trajectory
specifies local trajectory  at
at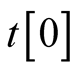 .
.
Since we move downward, next triangle  is
is  and we obtain
and we obtain . Then,
. Then,
 specifies local trajectory
specifies local trajectory  at
at  and next traingle
and next traingle  is
is . Continuing the process, we obtain a closed trajectory of length 10.
. Continuing the process, we obtain a closed trajectory of length 10.
Finally, we consider variation of gradient, i.e., “second derivative”, along a trajectory. Thanks for the smoothness condition, variation of gradient along a trajectory could be specified as a binary valued sequence.
Definition 12. Let  be a trajectory induced by
be a trajectory induced by  for tangent cone
for tangent cone . Then, “second derivative”
. Then, “second derivative”  of
of  along
along  is defined as a {U, D}-valued function:
is defined as a {U, D}-valued function:

where  and
and .
.
Then, we could encode the conformation of a trajectory by the second derivative along the trajectory. As an example, let’s consider the trajectory of Figure 2 again. First, set any initial value: . Then, since the first two triangles
. Then, since the first two triangles  and
and  have the same gradient,
have the same gradient, . The value of the second derivative is D until
. The value of the second derivative is D until , where it is changed to U because the gradient of
, where it is changed to U because the gradient of  is different from that of
is different from that of . Continuing the process, we obtain a binary sequence of length 10, DDDUDUUUDU, which describes the shape swept by the trajectory of triangles.
. Continuing the process, we obtain a binary sequence of length 10, DDDUDUUUDU, which describes the shape swept by the trajectory of triangles.
3. Encoding of Protein Backbone Structure
In the case of n = 3, we obtain a flow of 3-simplices (tetrahedrons), which is used for protein structure analysis. In this section we propose a simple encoding method which translates the conformation of a protein backbone into a sequence of letters from a 16-letter alphabet (called D2 codes), using the second derivative along trajectories of tetrahedrons.
First, we consider all the fragments of five amino-acids occurred in a protein. Each fragment is approximated by a tetrahedron sequence of length five, where we permit translation and rotation during the process to absorb irregularity inherent in actual protein structures.
Next, we compute the second derivative along the tetrahedron sequences to obtain binary-valued sequences of length five. We assign the binary-valued sequences, which are denoted as a base-32 number, to the center amino-acid of the corresponding fragment. For example, DDDUD is denoted by “2”, DUDDU is denoted by “9”, DUDUD is denoted by “A”, and so on.

Figure 2. Closed trajectory of 2-simplices induced by .
.

Figure 3. D2-encoding of a protein (transferase 1RKL).
Then, we obtain a one-dimensional representation of protein backbone structure by arranging the base-32 numbers in the order the corresponding amino-acids appear in the protein. See [1] for detailed description of the algorithm.
Figure 3 shows an example of D2-encoding of a protein. As you see, our method captures successfully not only recurring structural features of the protein (strand, turn, caps, helix), but also distortions (such as kink) as well.
4. Discussion
In this paper, we first describe the discrete differential geometry of n-simplices. Then, we apply the mathematical framework to analysis of protein structures and propose a simple encoding method which translates the conformation of a protein backbone into a 16-valued sequence.
Unlike previous works, our version of discrete differential geometry studies connection between space-filling n-simplices. Considering cones of an integer lattice, we have introduced tangent bundle-like structure on n-simplices naturally. On notable consequence is the smoothness condition, i.e., restriction on variation of gradient along a trajectory. In particular, we could encode the shape of n-dimensional objects if we approximate them by sweeping the occupied area with a trajectory of n-simplices.
As for protein structure analysis, since we do not use clustering analysis to encode local structures, our approach not only provides a intuitively understandable description of protein structures, but also covers wide varieties of distortions. Our method performs comparably with more sophisticated but more time-consuming methods which are specifically designed for protein structure analysis. In SHREC’10 Protein Model Classification we achieved results comparable to more sophisticated methods, using the length of the longest common subsequence as the measure of structural similarity [12] . At homology level of CATH95 data set, our method performs best among all the individual classifiers considered in [13] .