Existence Theory for Single Positive Solution to Fourth-Order Boundary Value Problems ()
1. Introduction
Fourth-order differential equations play an important role in various fields of science and engineering. With the help of boundary value conditions, we can describe the natural phenomena and mathematical model more accurately. Therefore, the fourth-order differential equations have received much attention and the theory and application have been greatly developed (see [1] -[4] and their references). Most of the results told us that the equations had at least single and multiple positive solutions. In papers [1] -[3] , the authors obtained some newest results for the singular fourth-order boundary value problems. But there is no result on the uniqueness of solution in them.
In this paper, we consider the following singular fourth-order boundary value problem:
 (1.1)
(1.1)
Throughout this paper, we always suppose that

Moreover,  may be singular at
may be singular at ,
,  , or
, or .
.
Equation (1.1) is often referred to as the deformation for an elastic beam under a variety of boundary conditions. A brief discussion of the physical interpretation under some boundary conditions associated with the linear beam equation can be found in Zill and Cullen [5] . In this article, we consider the existence and uniqueness of positive solutions for fourth-order singular boundary value problems by using mixed monotone method.
2. Preliminary
Let P be a normal cone of a Banach space E, and  with
with ,
, . Define
. Define

Now we give a definition(see [7] ).
Definition 2.1. Assume . A is said to be mixed monotone if
. A is said to be mixed monotone if  is nondecreasing in x and nonincreasing in y, i.e. if
is nondecreasing in x and nonincreasing in y, i.e. if  implies
implies  for any
for any , and
, and  implies
implies  for any
for any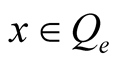 .
. 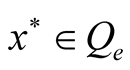 is said to be a fixed point of A if
is said to be a fixed point of A if .
.
Theorem 2.1. Suppose that  is a mixed monotone operator and
is a mixed monotone operator and  a constant
a constant ,
,  , such that
, such that
 (2.1)
(2.1)
Then A has a unique fixed point . Moreover, for any
. Moreover, for any 

satisfy

where

 , r is a constant from
, r is a constant from .
.
Theorem 2.2. (See [7] ): Suppose that  is a mixed monotone operator and
is a mixed monotone operator and  a constant
a constant  such that (2.1) holds. If
such that (2.1) holds. If  is a unique solution of equation
is a unique solution of equation

in , then
, then ,
, . If
. If , then
, then  implies
implies ,
,  , and
, and

3. Uniqueness Positive Solution of Problem (1.1)
This section discusses the problem
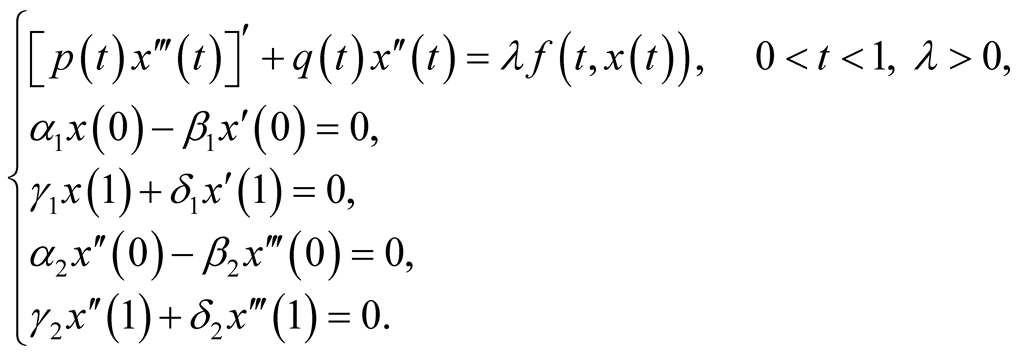
Throughout this section, we assume that
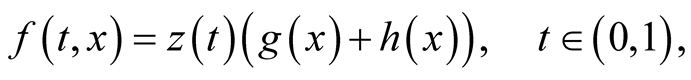 (3.1)
(3.1)
where
 (3.2)
(3.2)
Let  and
and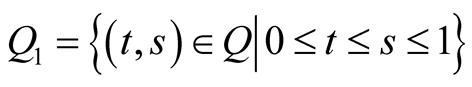 ,
, . We denote the Green’s functions for the following boundary value problems
. We denote the Green’s functions for the following boundary value problems

and

by  and
and , respectively. It is well known that
, respectively. It is well known that  and
and  can be written by
can be written by
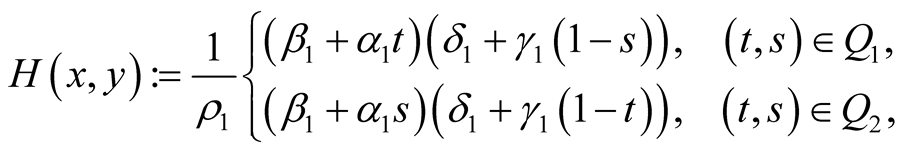
where  and
and

Lemma 3.1. Suppose that  holds, then the Green’s function
holds, then the Green’s function , possesses the following properties:
, possesses the following properties:
1)  is increasing and
is increasing and ,
, .
.
2)  is decreasing and
is decreasing and ,
, .
.
3) .
.
4) .
.
5)  is a positive constant. Moreover,
is a positive constant. Moreover, .
.
6)  is continuous and symmetrical over Q.
is continuous and symmetrical over Q.
7)  has continuously partial derivative over
has continuously partial derivative over ,
, .
.
8) For each fixed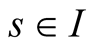 ,
,  satisfies
satisfies  for
for ,
,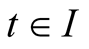 . Moreover,
. Moreover,  for
for .
.
9)  has discontinuous point of the first kind at
has discontinuous point of the first kind at  and
and

Following from Lemma 3.1, it is easy to see that
(a) 

(b) 
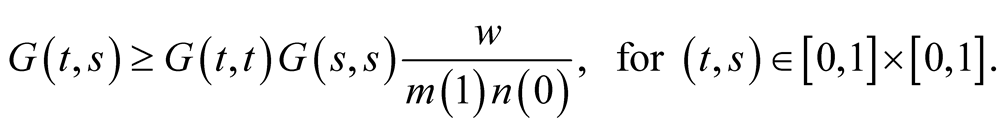
Suppose that x is a positive solution of (1.1). Then
 (3.3)
(3.3)
By using (3.3) and (a), we see that for every positive solution x one has

where . Let
. Let
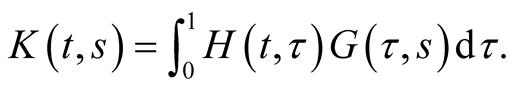
Thus by (3.3) one has
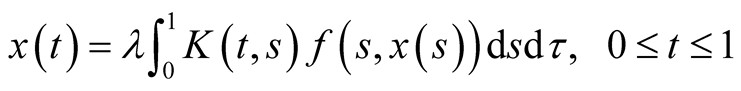
by (a) one has
 (3.4)
(3.4)
Let . Obviously, P is a normal cone of Banach space
. Obviously, P is a normal cone of Banach space .
.
Theorem 3.1. Suppose that there exists  such that
such that
 (3.5)
(3.5)
for any  and
and , and
, and  satisfies
satisfies
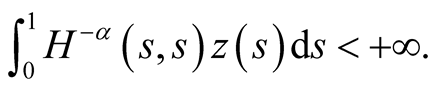 (3.6)
(3.6)
Then (1.1) has a unique positive solution . And moreover,
. And moreover,  implies
implies ,
,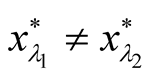 . If
. If , then
, then

Proof. Since (3.5) holds, let , one has
, one has

then
 (3.7)
(3.7)
Let . The above inequality is
. The above inequality is
 (3.8)
(3.8)
From (3.5), (3.7) and (3.8), one has
 (3.9)
(3.9)
Similarly, from (3.5), one has
 (3.10)
(3.10)
Let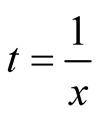 ,
, 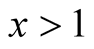 , one has
, one has
 (3.11)
(3.11)
Let . It is clear that
. It is clear that , and now let
, and now let
 (3.12)
(3.12)
where 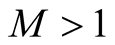 is chosen such that
is chosen such that
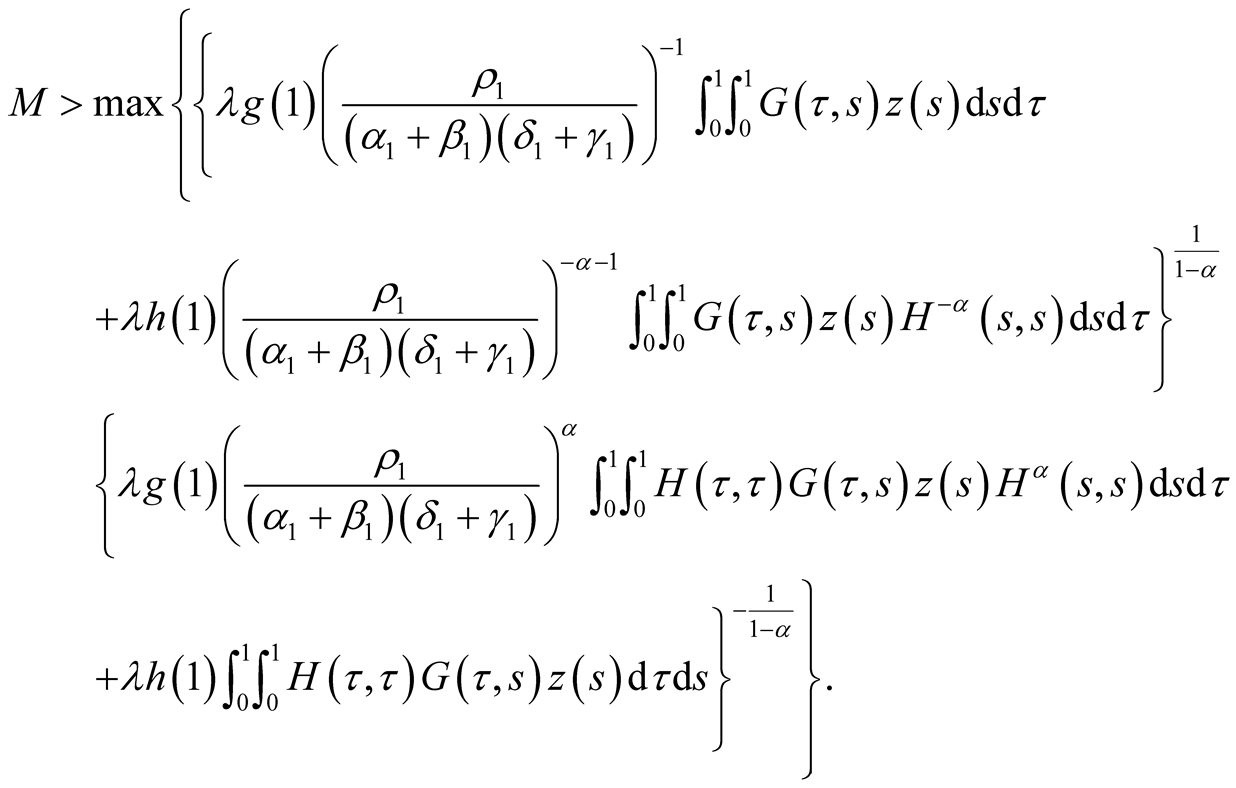
For any , we define
, we define
 (3.13)
(3.13)
First we show that . Let
. Let , from (3.10) and (3.11) we have
, from (3.10) and (3.11) we have

and from (3.9) we have
 (3.14)
(3.14)
Then from (3.4) and (3.13) we have
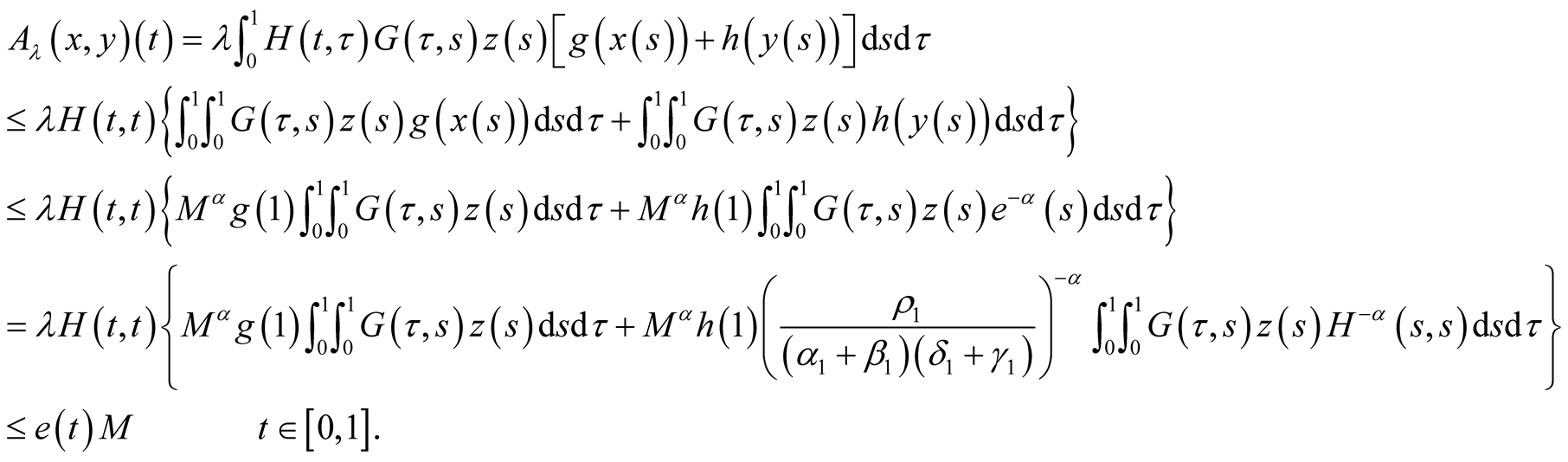
On the other hand, for any , from (3.9) and (3.10), we have
, from (3.9) and (3.10), we have
 (3.15)
(3.15)
Thus, from (3.15), we have

So,  is well defined and
is well defined and 
Next, for any , one has
, one has

So the conditions of Theorems 2.1 and 2.2 hold. Therefore there exists a unique  such that
such that
 . It is easy to check that
. It is easy to check that  is a unique positive solution of (1.1) for given
is a unique positive solution of (1.1) for given . MoreoverTheorem 2.2 means that if
. MoreoverTheorem 2.2 means that if  then
then ,
,  , and if
, and if , then
, then

This completes the proof.
Example. Consider the following singular fourth-order boundary value problem:

where , satisfies
, satisfies .
.
Let

Thus  and for any
and for any 
 ,
,  ,
,
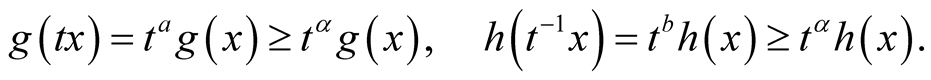
Now Theorem 3.1 guarantees that the above equation has a positive solution.
Funding
Project was supported by Heilongjiang Province Education Department Natural Science Research Item, China (12541076).