Solution of Multi-Delay Dynamic Systems by Using Hybrid Functions ()
1. Introduction
Delays occur frequently in biological, chemical, transportation, electronic, communication, manufacturing and power systems [1] . Time-delay and multi-delay systems are therefore very important classes of systems whose control and optimization have been of interest to many investigators [2] -[5] . While modeling such phenomena naturally requires the use of various systems, in many problems, such systems can not be solved explicitly. Therefore, it is important to find their approximate solutions by using some numerical methods. In recent years, the hybrid functions consisting of the combination of the Block-Pulse functions with the Chebyshev polynomials [6] , the Legendre polynomials [7] [8] , or the Taylor series [9] [10] have been shown to be a mathematical power tool for discretization of selected problems. Among these three hybrid functions, hybrids of the BlockPulse functions with the Legendre polynomials have been shown to be computationally more effective.
Recently a new hybrid function consisting of the combination of the Block-Pulse functions with the Bernoulli polynomials is presented [11] [12] . The advantages of the Bernoulli polynomials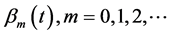 , over shifted the Legendre polynomials are:
, over shifted the Legendre polynomials are:
• The operational matrix , in the Bernoulli polynomials, has less errors than
, in the Bernoulli polynomials, has less errors than  for shifted the Legendre polynomials for
for shifted the Legendre polynomials for . This is because for
. This is because for 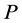 in
in 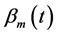 we ignore the term
we ignore the term  while for
while for  in
in  we ignore the term
we ignore the term .
.
• The Bernoulli polynomials have less terms than shifted the Legendre polynomials. For example , has 5 terms while
, has 5 terms while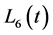 , has 7 terms, and this difference will increase by increasing m. Hence for approximating an arbitrary function we use less CPU time by applying the Bernoulli polynomials as compared to the shifted Legendre polynomials.
, has 7 terms, and this difference will increase by increasing m. Hence for approximating an arbitrary function we use less CPU time by applying the Bernoulli polynomials as compared to the shifted Legendre polynomials.
• The coefficient of individual terms in the Bernoulli polynomials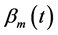 , is smaller than the coefficient of individual terms in the shifted Legendre polynomials
, is smaller than the coefficient of individual terms in the shifted Legendre polynomials . Since the computational errors in the product are related to the coefficients of individual terms, the computational errors are less by using the Bernoulli polynomials.
. Since the computational errors in the product are related to the coefficients of individual terms, the computational errors are less by using the Bernoulli polynomials.
In the present paper, we use the hybrid functions consisting of the combination of the Block-Pulse functions and the Bernoulli polynomials to solve the MDS. The method is based on converting the MDS into a system of multi-delay integral equations through integration. To eliminate integral operations, the unknown functions and various functions involved in the equations are approximated by the hybrid function and the operational matrices are used. To this end, operational matrices of multi-delay systems for the hybrid function are given. It will be seen that the operational matrices have many zero elements and are more sparse than the Legendre polynomials. These matrices are used to reduce the solution of MDS to the solution of a system of linear algebraic equations.
The paper is organized as follows: In Section 2, we describe the basic properties of the hybrid functions of the Block-Pulse and the Bernoulli polynomials required for our subsequent development. Section 3 is devoted to the formulation of linear time-varying multi-delay systems and the proposed numerical method is applied to the MDS. And in Section 4, we report our numerical findings and demonstrate the accuracy of the proposed scheme by considering some numerical examples. Finally, Section 5 gives some brief conclusions.
2. Hybrid of the Block-Pulse Functions and the Bernoulli Polynomials
Hybrid functions , are defined on the interval
, are defined on the interval 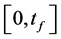 as [11]
as [11]
 (1)
(1)
where 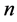 and
and  are the order of the Block-Pulse functions and the Bernoulli polynomials, respectively. The Bernoulli polynomials of order
are the order of the Block-Pulse functions and the Bernoulli polynomials, respectively. The Bernoulli polynomials of order 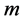 are defined in [13] by
are defined in [13] by

where , are the Bernoulli numbers. These numbers are a sequence of signed rational numbers that arise in the series expansion of trigonometric functions [14] and can be defined by the identity
, are the Bernoulli numbers. These numbers are a sequence of signed rational numbers that arise in the series expansion of trigonometric functions [14] and can be defined by the identity

Let  be an arbitrary element in
be an arbitrary element in , there exist unique coefficients
, there exist unique coefficients  such that [11]
such that [11]

where
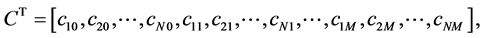
and

By using Equation (2) we obtain


where 
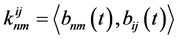 , and
, and 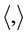 denotes the inner product. So we get
denotes the inner product. So we get
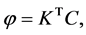
with


where  is a matrix of order
is a matrix of order  and is given by
and is given by
 (2)
(2)
Integration of the vector  defined in Equation (4) can be approximated by
defined in Equation (4) can be approximated by
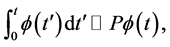 (3)
(3)
where 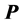 is the
is the  operational matrix for integration and is given by [11]
operational matrix for integration and is given by [11]
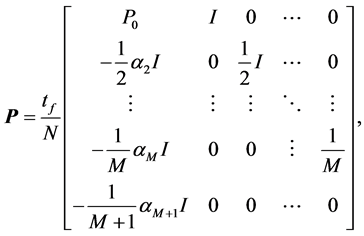 (4)
(4)
where 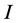 and
and 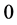 are the
are the  identity and zero matrices, respectively, and
identity and zero matrices, respectively, and
 (5)
(5)
The following property of the product of two hybrid function vectors will also be used. Let
 (6)
(6)
where 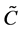 is a
is a  product operational matrix. To illustrate the calculation procedure see [11] .
product operational matrix. To illustrate the calculation procedure see [11] .
Multi-Delay Operational Matrix
The delay functions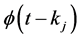 ,
,  are the shift of the function
are the shift of the function  defined in Equation (4), along the time axis by
defined in Equation (4), along the time axis by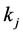 , where
, where  are rational numbers in
are rational numbers in . It is assumed without loss of generality that
. It is assumed without loss of generality that . If we expand
. If we expand 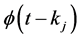 in terms of
in terms of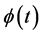 , we find
, we find

where  is the
is the  delay operational matrix of hybrid functions corresponding to
delay operational matrix of hybrid functions corresponding to  and is given by
and is given by
 (7)
(7)
where elements of the delay matrix are the  matrix
matrix 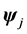 given by
given by
 (8)
(8)
It is noted that the first 1 in the first row is located at the  th column where
th column where

We define 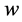 as the smallest positive integer number for which
as the smallest positive integer number for which 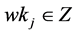 for
for  and
and 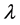 is the greatest common divisor of the integers
is the greatest common divisor of the integers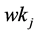 ,
,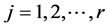 .
.
3. Problem Statement and Approximation Using Hybrid Functions
Consider the following linear time multi-delay dynamic systems:
 (9)
(9)
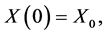 (10)
(10)
 (11)
(11)
where ,
, 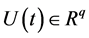 ,
,  and
and ,
,  , are matrices of appropriate dimensions,
, are matrices of appropriate dimensions, 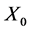 is a constant specified vector, and
is a constant specified vector, and 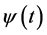 is an arbitrary known function. The problem is to find
is an arbitrary known function. The problem is to find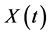 ,
, 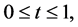 satisfying Equations (13) and (14). Let
satisfying Equations (13) and (14). Let
 (12)
(12)
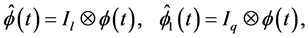 (13)
(13)
where  and
and  are the
are the  and
and 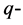 dimensional identity matrices,
dimensional identity matrices,  is
is  vector and
vector and  denotes the Kronecker product [15] . Using the property of the Kronecker product,
denotes the Kronecker product [15] . Using the property of the Kronecker product,  and
and  are matrices of order
are matrices of order  and
and , respectively. Assume that each
, respectively. Assume that each  and each of
and each of ,
,  ,
, 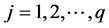 , can be written in terms of hybrid functions as
, can be written in terms of hybrid functions as

Then, using Equations (15) and (16), we have
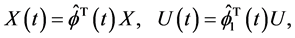 (14)
(14)
where 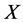 and
and  are vectors of order
are vectors of order  and
and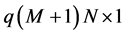 , respectively, given by
, respectively, given by
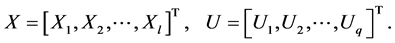
Similarly, we have
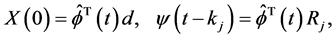 (15)
(15)
where 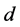 and
and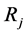 ,
,  , are vectors of order
, are vectors of order  given by
given by
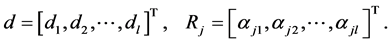
Let approximate  and
and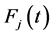 ,
,  , by Equations (2)-(4) as follows
, by Equations (2)-(4) as follows
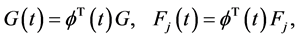 (16)
(16)
where ,
,  are of dimensions
are of dimensions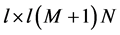 , and
, and  is of dimension
is of dimension .
.
We can also write ,
, 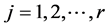 , in terms of the hybrid functions as
, in terms of the hybrid functions as

where

and  is the delay operational matrix. Moreover
is the delay operational matrix. Moreover
 (17)
(17)
 (18)
(18)
where
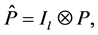
and

where ,
, 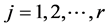 , are constant matrices of order
, are constant matrices of order . Note
. Note  is
is  product operational matrix that to illustrate the calculation procedure we choose
product operational matrix that to illustrate the calculation procedure we choose 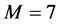 and
and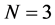 . Thus we have
. Thus we have

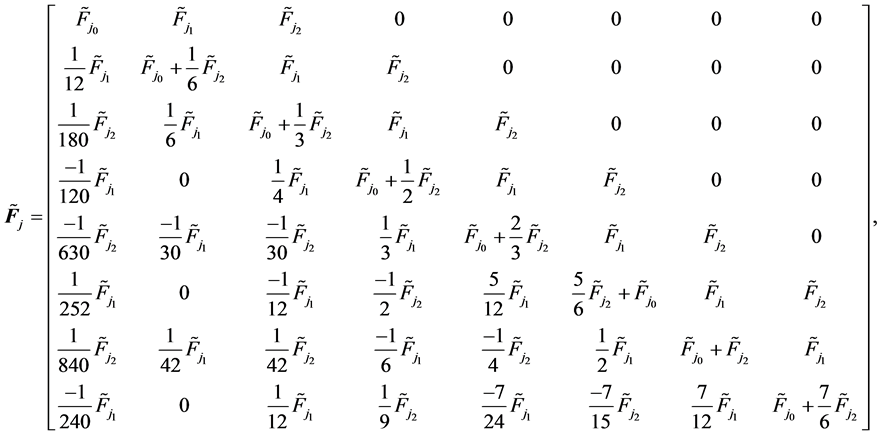 (19)
(19)
where  and
and , are the
, are the  matrices given by
matrices given by

By integrating Equation (12) from  to
to 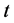 and using Equations (15)-(22), we have
and using Equations (15)-(22), we have
 (20)
(20)
simplifying Equation (23) we obtain
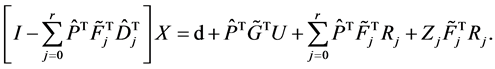 (21)
(21)
by solving the set of linear algebraic equations Equation (24), we obtain the coefficients vector .
.
4. Numerical Implementation
In this section, to give a clear overview of the analysis method presented and to demonstrate the applicability and accuracy of the method three examples are given.
Example 1. Consider the multi-delay dynamic system from [7] described by
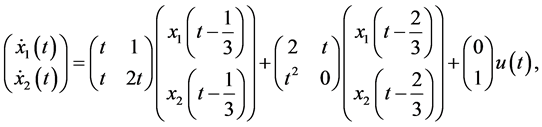 (22)
(22)
with
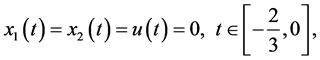 (23)
(23)
and
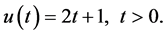 (24)
(24)
The exact solutions are
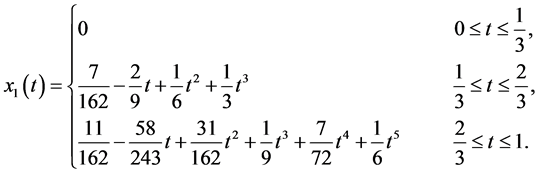

To solve this problem by the hybrid functions, we select  and
and . Let
. Let
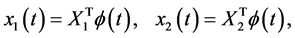 (25)
(25)
where ,
, 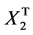 and
and 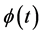 can be obtained similarly to Equations (3) and (4). By expanding
can be obtained similarly to Equations (3) and (4). By expanding  and
and  in terms of the hybrid functions we get
in terms of the hybrid functions we get
 (26)
(26)
 (27)
(27)
Therefore, we have
 (28)
(28)
 (29)
(29)
where 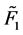 and
and 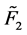 the 24 × 24 matrices, can be calculated as Equation (19). Also D1 and D2 are the 24 ×24 delay operational matrices given by
the 24 × 24 matrices, can be calculated as Equation (19). Also D1 and D2 are the 24 ×24 delay operational matrices given by

where

Integrating Equation (25) from  to
to 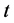 and using Equations (26)-(27) and substituting Equations (28)-(32) we get
and using Equations (26)-(27) and substituting Equations (28)-(32) we get
 (30)
(30)
where  is the operational matrix of integration given in Equation (7). By solving Equation (33) the values of
is the operational matrix of integration given in Equation (7). By solving Equation (33) the values of  and
and  can be found as
can be found as
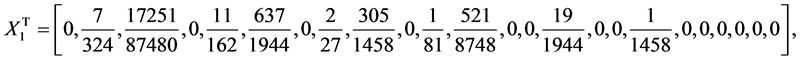
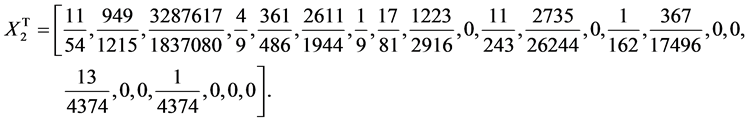
To define 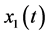 and
and 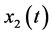 for
for  in the interval
in the interval 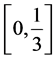 we map
we map  into
into  by mapping
by mapping  into
into , and for
, and for  in the interval
in the interval  we map this interval into
we map this interval into  by mapping
by mapping  into
into , and similarly for the other intervals. From Equation (28) we get
, and similarly for the other intervals. From Equation (28) we get
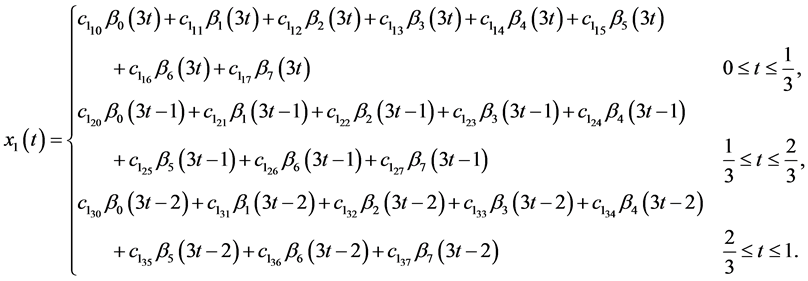
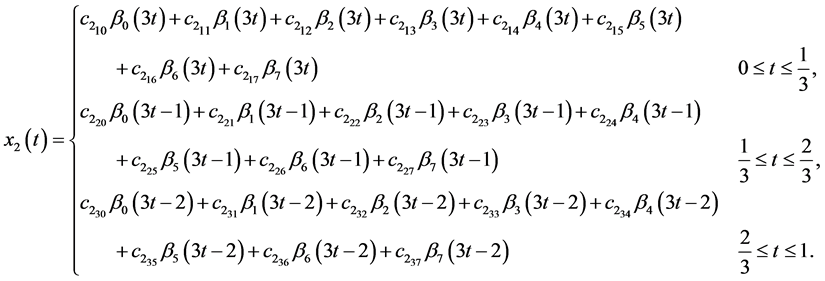
After simplifying the same value as the exact  and
and  would be obtained.
would be obtained.
Example 2. Consider the delay dynamic system described by
 (31)
(31)
with
 (32)
(32)
and
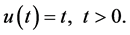 (33)
(33)
The exact solutions are


To solve this problem by using of the hybrid functions, we select  and
and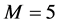 . Let
. Let
 (34)
(34)
where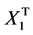 ,
,  and
and  can be obtained similarly to Equations (3)-(4). Using Equation (37) we get
can be obtained similarly to Equations (3)-(4). Using Equation (37) we get

where  is the
is the  delay operational matrix given by
delay operational matrix given by

where
 (35)
(35)
By expanding  in terms of hybrid functions we obtain
in terms of hybrid functions we obtain
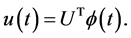 (36)
(36)
Integrating Equation (34) from  to
to 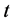 and using Equations (35)-(36) and substituting Equations (37)-(39), we get
and using Equations (35)-(36) and substituting Equations (37)-(39), we get
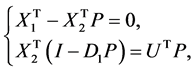 (37)
(37)
where  is the operational matrix of integration given in Equation (7). By solving Equation (40) the values of
is the operational matrix of integration given in Equation (7). By solving Equation (40) the values of 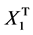 and
and  can be found. By using from Equation (37) and simplifying the same value as the exact
can be found. By using from Equation (37) and simplifying the same value as the exact  and
and 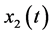 would be obtained.
would be obtained.
Example 3. Consider the following multi-delay system with delay in both control and state described by
 (38)
(38)
with
 (39)
(39)
and
 (40)
(40)
The exact solutions are
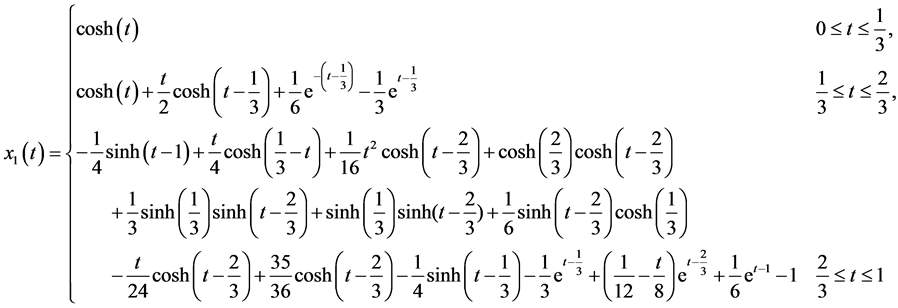
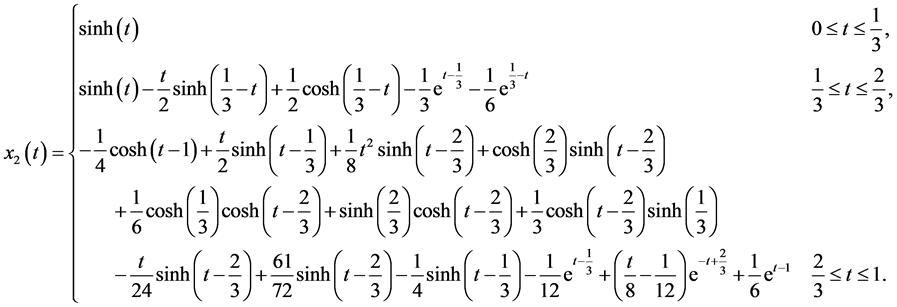
To solve this problem by using the hybrid functions, we select  and
and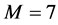 . Let
. Let
 (41)
(41)
where ,
,  and
and  can be obtained similarly to Equations (3) and (4). By expanding
can be obtained similarly to Equations (3) and (4). By expanding  and
and  in terms of hybrid functions we get
in terms of hybrid functions we get
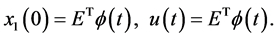 (42)
(42)
Using Equation (44) and (45) we obtain
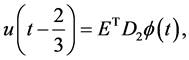 (43)
(43)
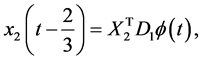
where  and
and 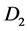 are the
are the 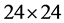 delay operational matrices given by
delay operational matrices given by
 (44)
(44)
where

By integrating Equation (41) from 0 to t and using Equations (42) and (43) and substituting Equations (44) and (47), we get
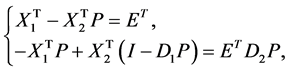 (45)
(45)
where  is the operational matrix of integration given in Equation (7). By solving Equation (48) the values of
is the operational matrix of integration given in Equation (7). By solving Equation (48) the values of  and
and 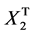 can be found. By using from Equation (44) and simplifying the same value as the exact
can be found. By using from Equation (44) and simplifying the same value as the exact  and
and 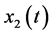 would be obtained. In Table 1 a comparison is made between the exact solution and the approximation solution of
would be obtained. In Table 1 a comparison is made between the exact solution and the approximation solution of  and
and  for
for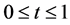 . The approximation value of
. The approximation value of 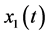 and
and  on
on , is the same as the exact solution.
, is the same as the exact solution.
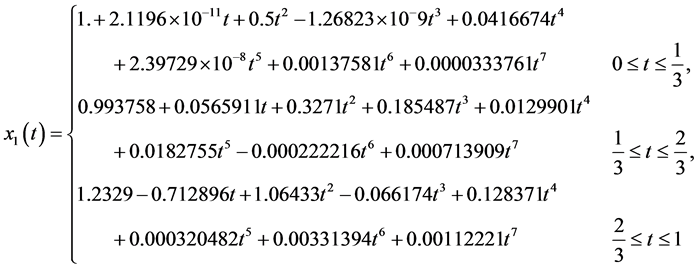


Table 1. Approximate solutions and exact solutions of Example 3.
5. Conclusion
The hybrid of the Block-Pulse functions and the Bernoulli polynomials and the associated operational matrices of integration and delay are applied to solve the linear multi-delay dynamic systems. The method is computationally very attractive, at the same time keeping the accuracy of the solution. It is also shown that the hybrid functions provide exact solutions in each subintervals for Examples 1, 2 and 3. The presented method reduces multi-delay systems to the solution a system of algebraic equations, and so the calculation is easy. The matrices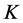 ,
,  and
and  in Equations (5), (7) and (10) are sparse, hence the present method is very attractive and reduces the CPU time and computer memory.
in Equations (5), (7) and (10) are sparse, hence the present method is very attractive and reduces the CPU time and computer memory.
NOTES
*Corresponding author.