Unbiased Diffusion to Escape Complex Geometries: Is Reduction to Effective One-Dimensional Description Adequate to Assess Narrow Escape Times? ()
1. Introduction
The unbiased motion of point particles confined within quasi-one-dimensional systems, such as pores and channels, has drawn great interest in recent years, due to the ubiquity of these systems in nature and technology [1] - [3] . The problem of spatially-constrained diffusion arises from different contexts of practical and theoretical interest, and is relevant to nanotechnology, chemistry, and biology, having direct applications to channels such as pores in zeolites [4] , carbon nanotubes [5] , synthetic nanopores [6] -[8] , artificial pores produced in solid thin films [9] , channels in biological systems [10] , and single-nanopore sensors, designed to detect, quantify, and characterize many different types of molecules, for example, singleand double-stranded DNA chains.
Experimental techniques, such as high-resolution crystallography of bacterial porins and other large channels, have demonstrated that these can be envisaged as tubes with significantly varying cross-sections along their principal axis. In some of these channels, variations in cross-section areas exceed one order of magnitude [11] [12] . This leads to the so-called entropic-like walls and barriers in the theoretical description of transport through such structures.
When diffusion occurs in quasi-one-dimensional structures, it is intuitively appealing to introduce an effective one-dimensional description. In a three-dimensional tube of varying radius  with the
with the  -axis directed along the centerline of the tube, the one-dimensional concentration of point particles
-axis directed along the centerline of the tube, the one-dimensional concentration of point particles  is related to their three-dimensional concentration
is related to their three-dimensional concentration 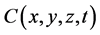 by the relationship
by the relationship
 (1)
(1)
Here, 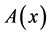 is the position-dependent cross-section area of the tube, where integration is carried out. Given the condition of uniform distribution of particles in any cross-section,
is the position-dependent cross-section area of the tube, where integration is carried out. Given the condition of uniform distribution of particles in any cross-section,  , obeys the Fick-Jacobs equation, then
, obeys the Fick-Jacobs equation, then
 (2)
(2)
where  is the particle’s diffusion coefficient in free space. Robert Zwanzig [13] generalized this result, showing that the diffusion coefficient entering into (2) becomes position-dependent,
is the particle’s diffusion coefficient in free space. Robert Zwanzig [13] generalized this result, showing that the diffusion coefficient entering into (2) becomes position-dependent,  , provided the radius is a slowly varying function of x, i.e.,
, provided the radius is a slowly varying function of x, i.e.,
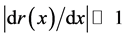 (3)
(3)
Therefore, the generalized Fick-Jacobs equation takes the form,
 . (4)
. (4)
Zwanzig also derived the following expression for :
:
 (5)
(5)
Later, Reguera and Rubí [14] generalized this result and suggested,
 (6)
(6)
In an earlier numerical study [15] , the generalized Fick-Jacobs Equation (4), with  given by (6), was shown to be valid for
given by (6), was shown to be valid for
 , (7)
, (7)
which compared with the requirement expressed by (3), is less restrictive, thus giving the generalized Fick-Jacobs equation a considerably extended range of applicability. Kalinay and Percus [16] [17] developed a more general theory of reduction to the effective one-dimensional description for radially symmetrical 2D tubes, and Dagdug and Pineda [18] extended these results to non-symmetrical 2D systems.
A wide range of stochastic processes of practical interest underlies first-passage events, such as the first-passage time, namely, the probability that a diffusing particle or a random walk will first reach a specified site (or set of sites) at a specified time [19] . Indeed, chemical and biochemical reactions [20] [21] , animals searching for food [22] , and trafficking receptors on biological membranes [23] , are often controlled by first-encounter events [24] . The narrow escape time (NET)—the mean time a Brownian particle spends before being trapped by an opening window in exiting the cavity for the first time—is of particular importance. Its applications range from cellular biology to biochemical reactions in cellular micro-domains, such as dendritic spines, synapses, and micro-vesicles, among others [23] [25] . The NET is the limiting quantity and the first step in the mathematical modeling of such processes where particles must first exit their domains in order to live up to their biological function [24] .
To determine which form of  to use in (4) for a given set of geometries and boundary conditions, we took advantage of the fact that the Mean First-Passage Time (MFPT),
to use in (4) for a given set of geometries and boundary conditions, we took advantage of the fact that the Mean First-Passage Time (MFPT), 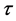 , is a quantity often obtained by means of computer simulations. Then, the MFPT—defined as the time it takes a random walker to reach a specified place for the first time, averaged over all the trajectories or realizations of the random walk—is found to satisfy a backward equation,
, is a quantity often obtained by means of computer simulations. Then, the MFPT—defined as the time it takes a random walker to reach a specified place for the first time, averaged over all the trajectories or realizations of the random walk—is found to satisfy a backward equation,
 , (8)
, (8)
where  (
(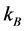 is the Boltzmann constant and T the absolute temperature), and the potential
is the Boltzmann constant and T the absolute temperature), and the potential , is defined as follows,
, is defined as follows,
 (9)
(9)
Equation (9) accounts for the change in cross-section area along the axial length of the tube, taken to be zero at  (a reference position). Then (8) is solved for the appropriate boundary conditions, to obtain an algebraic expression that relates
(a reference position). Then (8) is solved for the appropriate boundary conditions, to obtain an algebraic expression that relates  with
with  and the system’s geometrical parameters.
and the system’s geometrical parameters.
Following a previous study of narrow escape times in a spherical cavity with two holes [26] , this paper proposes a system made by juxtaposing two identical semi-cones of length L, by their larger radii, as shown in Figure 1, and solves the generalized backward Equation (8) for 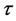 with different expressions of
with different expressions of . Computer simulations were carried out for comparison with theoretical predictions across a wide range of geometrical parameter values for the proposed system. The potential use of the equations obtained to assess narrow escape times is then discussed.
. Computer simulations were carried out for comparison with theoretical predictions across a wide range of geometrical parameter values for the proposed system. The potential use of the equations obtained to assess narrow escape times is then discussed.
2. Theory and Simulations
To solve (8), we refer to Figure 2, and the boundary conditions described thereunder. Given the tube’s radius as a function of the axial coordinate,  ,
, 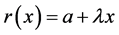 , the cross-section area is given by
, the cross-section area is given by
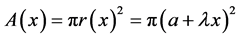 .
.
Then, by choosing the reference position  we found, from (9),
we found, from (9),
 .
.
And from here, we rewrote (8) as follows,

Figure 1. The tube of varying cross-section studied in this work. The slope of the tube’s wall, with length 2L, has the absolute value λ, and the major radius b is given by a + λL. This system can be taken as a narrow escape time problem, as stated by Grigoriev et al. [27] .
 (10)
(10)
which is a separable ordinary differential equation. At this point, we did not need to choose an explicit for , as this was done in due time using (5) and (6). Now, the first integration of (10) yields,
, as this was done in due time using (5) and (6). Now, the first integration of (10) yields,
 , (11)
, (11)
Here, we used the boundary condition of zero flux in the reflecting wall at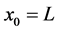 , to find the value of the integration constant to be
, to find the value of the integration constant to be
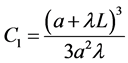 .
.
Applying this result to (11), after some algebra it became,
 , (12)
, (12)
where we used the fact that , either from (5) or (6), is a function only of the first derivative of
, either from (5) or (6), is a function only of the first derivative of , a linear function of
, a linear function of , and therefore, a constant, denoted here as
, and therefore, a constant, denoted here as . Thus, we can integrate (12) a second time to yield,
. Thus, we can integrate (12) a second time to yield,
 . (13)
. (13)
Then, by using the second boundary condition, a perfectly absorbent wall at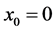 , we found
, we found ,
,
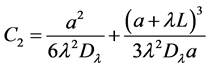 .
.
With this result in (13), we manipulated the resulting expressions to yield,
 , (14)
, (14)
which is one of the main results of this work. Here, we used . Furthermore, evaluating (14) at the reflecting wall’s position,
. Furthermore, evaluating (14) at the reflecting wall’s position,  , and setting
, and setting , one finds
, one finds
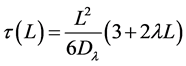 which is a known result previously reported by Berezhkovskii et al. [15] .
which is a known result previously reported by Berezhkovskii et al. [15] .
The second result is obtained by averaging  over the entire range of variation of x0, namely
over the entire range of variation of x0, namely , thus defining this average as follows,
, thus defining this average as follows,
 . (15)
. (15)
Then, after some algebra, we can write the general result:
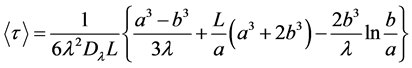 . (16)
. (16)
Along with (14) and (16), we can use any expression of , namely,
, namely,
 , (17)
, (17)
or from (5) or (6),
 . (18)
. (18)
For subsequent comparisons, we will use (18) only, as it has been shown to yield better results in previous works.
In simulations, we found the mean first-passage time,  (MFPT), defined above. The particle’s initial position,
(MFPT), defined above. The particle’s initial position,  , is distributed uniformly within the cavity’s volume. The MFPT is denoted as
, is distributed uniformly within the cavity’s volume. The MFPT is denoted as . When running simulations, we took
. When running simulations, we took ,
,  and the time step
and the time step , so that
, so that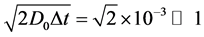 . The actual particle’s position,
. The actual particle’s position,  , is given by
, is given by , where
, where  is the previous position, and
is the previous position, and 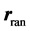 is a vector of pseudo-random numbers generated with a Gaussian distribution (
is a vector of pseudo-random numbers generated with a Gaussian distribution ( ,
, ). Each MFPT was obtained by averaging the first-passage times of
). Each MFPT was obtained by averaging the first-passage times of 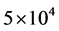 trajectories.
trajectories.
3. Results and Discussion
Figure 3 and Figure 4 show the main comparisons made in this work between MFPT obtained by computer simulations and theoretical predictions from Equation (16) using Reguera-Rubí’s effective diffusion coefficient (18). Both figures show good agreement virtually across the entire range of parameter values. Each point in Figure 3 is related to a system of fixed volume (arbitrarily chosen to be the unit sphere), so the main difference would be the size of the absorbent windows. For such purpose, while keeping L constant and varying a parametrically,  should be a function of these parameters, as follows,
should be a function of these parameters, as follows,

Figure 3. Mean first-passage time as a function of the parameter a/L, absorbent window’s size over the tube’s semi-length. Each point corresponds to a different value of λ, chosen to fix the system’s volume at a constant value (arbitrarily set as the volume of a sphere of unit radius). The theoretical curve (solid line) corresponds to Equation (16), with Dλ given in (18), and 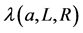 from (19).
from (19).

Figure 4. Mean first-passage times as a function of the parameter λ, keeping the value of the absorbent window’s radius constant. Two sets of data, obtained from simulations, are shown: for a = 0.05 (triangles), and a = 0.35 (circles); both theoretical curves (dashed lines) correspond to Equation (16), with Dλ from (18).
 . (19)
. (19)
Then, the particles will have to explore a volume of the same size, but different radii of aperture to escape. As expected, survival times grow unbounded  as the aperture to escape from the domain tends to close
as the aperture to escape from the domain tends to close .
.
Back to the narrow escape problem, in 2002, I. V. Grigoriev et al., studied the time-dependence of the survival probability of a Brownian particle that escapes from a cavity through a round hole [27] . Two main results were reported: Firstly, algebraic proof that decay is exponential for small holes, based on the spectral representation of the survival probability, and secondly, that the expression for the rate constant in terms of the problem parameters (the diffusion constant D of the particles, the hole radius a, and the cavity volume V) is given by,
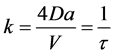 . (20)
. (20)
In their work, they also ran Brownian dynamics simulations to calculate the survival probability in spherical and cubic cavities for different values of the absorbing-window’s radius. They also found that when a is small enough, decay is exponential, and the rate constants found in simulations are in good agreement with those predicted by (20).
Previously, a work by Vázquez and Dagdug [26] , theoretically and numerically studied a first-passage problem with this technique, which fits naturally in the NET category as one varies the positive constant a, i.e., the aperture’s radius. In that work, the expressions found fit the simulation data with great accuracy. Therefore, we now compared Equations (16) with  from (18), against the MFPTs (survival times) from simulations. Figure 4 shows, for two constant window sizes,
from (18), against the MFPTs (survival times) from simulations. Figure 4 shows, for two constant window sizes,  (circles), and
(circles), and 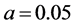 (triangles), the variation of survival times of Brownian particles as a function of the slope of the tube’s wall,
(triangles), the variation of survival times of Brownian particles as a function of the slope of the tube’s wall,  , as a geometrical parameter. In both cases, we found good agreement between theoretical and computer data across a wide range of values of
, as a geometrical parameter. In both cases, we found good agreement between theoretical and computer data across a wide range of values of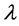 , although slight deviations did occur at greater values of
, although slight deviations did occur at greater values of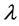 . Even though such deviations are expected to grow larger as
. Even though such deviations are expected to grow larger as  increases, there is still a wide interval where agreement is good.
increases, there is still a wide interval where agreement is good.
Finally, we obtained algebraic expressions (14) and (16) for the first-passage time of Brownian particles through the effective one-dimensional description of diffusion. These expressions, which are the main results of this work, are useful in assessing Narrow Escape Times in complex geometries, and fit well with simulated data for a wide range of values for this system’s geometrical parameters.
Acknowledgements
This work was carried out with the support of the CONACyT [Consejo Nacional de Ciencia y Tecnología-National Science and Technology Council], Project Grant No. 176452, and the computer infrastructure provided by the Universidad Autónoma Metropolitana. Y. Chávez thanks CONACyT (fellowship No. 269180). The authors are indebted to C. Reynaud for the critical reading of the manuscript and her useful comments.