Cautionary Remarks When Testing Agreement between Two Raters for Continuous Scale Measurements: A Tutorial in Clinical Epidemiology with Implementation Using R

Mohamed M. Shoukri

Department of Epidemiology and Biostatistics, Schulich School of Medicine and Dentistry, University of Western Ontario, London, Canada.

DOI: 10.4236/ojepi.2024.141005                

Abstract

Background: When continuous scale measurements are available, agreements between two measuring devices are assessed both graphically and analytically. In clinical investigations, Bland and Altman proposed plotting subject-wise differences between raters against subject-wise averages. In order to scientifically assess agreement, Bartko recommended combining the graphical approach with the statistical analytic procedure suggested by Bradley and Blackwood. The advantage of using this approach is that it enables significance testing and sample size estimation. We noted that the direct use of the results of the regression is misleading and we provide a correction in this regard. Methods: Graphical and linear models are used to assess agreements for continuous scale measurements. We demonstrate that software linear regression results should not be readily used and we provided correct analytic procedures. The degrees of freedom of the F-statistics are incorrectly reported, and we propose methods to overcome this problem by introducing the correct analytic form of the F statistic. Methods for sample size estimation using R-functions are also given. Results: We believe that the tutorial and the R-codes are useful tools for testing and estimating agreement between two rating protocols for continuous scale measurements. The interested reader may use the codes and apply them to their available data when the issue of agreement between two raters is the subject of interest.

Keywords

Limits of Agreement, Pitman and Morgan Tests, Test of Parallelism, The Arcsine Variance Stabilizing Transformation, Sample Size Estimation

1. Introduction

The subject of agreement between two or more raters is of interest to investigators who work in medical research as well as physical sciences. When continuous scale measurements are available, agreements between two measuring devices or medical diagnostic tools are assessed both graphically and analytically. In clinical investigations, Bland and Altman proposed [1] [2] suggested plotting subject-wise differences between raters against subject-wise averages. Bartko [3] recommended combining the graphical approach with the statistical analytic procedure based on linear regression models that were suggested by Bradley and Blackwood [4] .

According to Stephenson & Babiker [5] , “Clinical epidemiology can be defined as the investigation and control of the distribution and determinants of disease”. Last [6] felt that the term was an oxymoron, and that its increasing popularity in many different medical schools was a serious issue.

Clinical epidemiology aims to optimize the diagnostic, treatment and prevention processes for an individual patient, based on an assessment of the diagnostic and treatment process using epidemiological research data [7] . A central tenet of clinical epidemiology is that every clinical decision must be based on rigorously evidence-based science. The objectives of clinical epidemiology are primarily to develop epidemiologically sound clinical guidelines and standards for diagnosis, disease progression, prognosis, treatment and prevention. The data obtained in epidemiological studies are also applicable to the epidemiological justification of preventive programs for communicable and noncommunicable diseases [8] .

A key aspect of clinical epidemiology is the evaluation of the effectiveness of treatment and prevention medicines [8] . To deliver reliable results, the diagnoses must be reported error-free. Measures of reliability and agreements among diagnostic tools play an important role in this regard.

Reliability and agreement are important issues in disease diagnosis and classification, the development of screening tools, quality assurance, and the evaluation of diagnostic tools for clinical investigations (Kottner et al. [9] ).

When the responses are interval scale measurements the intraclass correlation is used to quantify reliability. When the measured responses are categorical the agreement between raters is quantified by the well-known “Kappa” coefficient. On the other hand, reliability is measured by the ICC. The concept of agreement between two raters when the responses are interval scale measurements is quantified by assessing both the bias and accuracy of the rating devices. The approach proposed by Bradley and Blackwood [4] is used to simultaneously test for bias and accuracy. Their test is obtained from the simple regression of the case-wise differences between the raters against the case-wise means of the ratings. In other words, we say that agreement between measuring devices or two raters exists if three conditions are satisfied: The two sets of measurements are highly correlated; the two methods are equally precise, and the two methods are unbiased relative to each other. The approach applies statistical testing jointly on the intercept and the slope. Testing the intercept equals zero is equivalent to testing for the absence of bias, while testing the slope equals zero is equivalent to equality of precisions. This joint test of intercept and slope coefficients in simple linear regression are not straightforward. Our main objective in this paper is to caution against the automatic results produced by commercial statistical programs for regression analysis and present alternative approaches. Issues of sample size estimation are discussed as well.

2. Methods

2.1. Wilk’s Tests

Let $\left(x_{i1},x_{i2}\right),i=1,2,\cdots ,n$ denote a random sample of size n drawn from a bivariate normal distribution whose parameters are $\left({\mu }_1,{\mu }_2,{\sigma }_1^2,{\sigma }_2^2,{\rho }_{12}\right)$ .

The summary statistics of the data are: ${\bar{X}}_1=mean\left(X_1\right),{\bar{X}}_2=mean\left(X_2\right)$ , $S_1^2=variance\left(X_1\right),S_2^2=variance\left(X_2\right)$ , and ${\rho }_{12}$ is the correlation between $X_1$ and $X_2$ .

The ultimate goal is to test the simultaneous null hypothesis $H_0:{\mu }_1={\mu }_2\cap$ ${\sigma }_1^2={\sigma }_2^2$, evaluate its power and determine approximately the sample size to achieve prespecified levels of power.

The above hypothesis has two components; the first is $H_0:{\sigma }_1^2-{\sigma }_2^2=0$ , which is testing the hypothesis that the two raters have equal precision. The second is $H_0:{\mu }_1-{\mu }_2=0$ , which is testing the hypothesis that the two raters are unbiased relative to each other.

The null hypothesis $H_0:{\mu }_1={\mu }_2\cap {\sigma }_1^2={\sigma }_2^2$ is an extension of the parallel test. Bradley and Blackwood [4] proposed a simple statistic to test the above hypothesis. This test has applications in agreement studies. Needless to say that separate statistics tests for the equality of the two means or the two variances are well-documented in statistical literature. To avoid multiplicity, researchers used Bonferroni correction by conducting separate tests of equality of means followed by testing equality of variances. This requires that the test size α be split into α/2 for testing the mean (using paired t-test) and α/2 is the size of the test of equality of two correlated variances (Morgan [10] and Pitman [11] ) known as Morgan-Pitman test.

The separate statistical tests for the equality of means or variances of two dependent variables are well-known, and using both of them for a simultaneous test of both null hypotheses requires the use of a Bonferroni correction.

The null hypothesis of equality of means is tested using the following statistic:

$Z_m=\frac{{\bar{X}}_1-{\bar{X}}_2}{\sqrt{S_1^2+S_2^2-2S_1{S}_2{\rho }_{12}}/\sqrt{n-1}}$ (1)

which has t-distribution with $\left(n-1\right)$ degrees of freedom when $H_0:{\mu }_1={\mu }_2$ is true.

On the other hand, the null hypothesis of equality of variances (equality of precisions) is tested using the statistic:

$z_v=\frac{\sqrt{n-2}\left(S_1^2-S_2^2\right)}{2S_1{S}_2\sqrt{1-{\rho }_{12}^2}}$ (2)

which has t-distribution with $\left(n-2\right)$ degrees of freedom when $H_0:{\sigma }_1^2={\sigma }_2^2$ is true.

Earlier, Wilks [11] [12] suggested tests of equality of correlated means and correlated variances using the statistic:

$Z_{mp}=\frac{S_1^2{S}_2^2\left(1-{\rho }_{12}^2\right)}{S^2\left(1+{\rho }_{12}\right)\left[S^2\left(1-{\rho }_{12}\right)+C\right]}$ (3)

where

$S^2=\frac{1}{2}\left[S_1^2+S_2^2\right]$

$C={\left({\bar{X}}_1-{\bar{X}}_2\right)}^2/2$

Then $Q=-2\log \left(Z_{mv}\right)~X_{\left(2\right)}^2$ .

2.2. Example

We apply the methodology presented in this paper on Serum Alanine aminotransferase ( ALT ). The ALT is a critical parameter for both the assessment and follow-up of patients with liver disease. Therefore, establishing the repeatability and the precision of ALT measurements as a diagnostic marker is of paramount importance. Regardless of gender or body mass index ( BMI ) [13] , the normal range was most often estimated from a population that included patients with subclinical liver disease, including non-alcoholic fatty liver disease (NAFLD), which is now documented as the greatest prevalent cause of chronic liver disease worldwide [14] . Recent studies have recommended establishing normal ranges for ALT separately in males and females [15] .

In a large tertiary hospital-based registry, the available data were collected from 30 males. The ALT levels were evaluated twice, once in the department of laboratory medicine (rate 1, and the values are denoted by $X_{i1}$ ) and once by the department of pathology (rater 2 and the values are denoted by $X_{i2}$ ).

Rater 1: Department of laboratory medicine.

Rater 2: Department of pathology.

ALT1<-c (6, 6, 67, 97, 57, 63, 55, 192, 212, 182, 317, 303, 62, 64, 64, 54, 54, 67, 68, 135, 68, 191, 262, 151, 70, 75, 76, 5, 6, 61, 74).

ALT2<-c (8, 8, 69, 99, 59, 63, 57, 191, 211, 184, 319, 305, 64, 66, 66, 56, 56, 69, 70, 137, 70, 193, 261, 153, 72, 77, 78, 5, 8, 63, 73).

The ALT data has the following summary statistics:

${\bar{X}}_1=106.967,{\bar{X}}_2=108.500,S_1=81.91,S_2=81.56$ and ${\rho }_{12}=0.999$ , and the sample size $n=30$ .

Therefore

$Z_m=-7.686\text{and}p\text{-value}=0.00001,$

This means that the hypothesis of the two raters are not unbiased relative to each other is supported by the data. On the other hand:

$Z_p=1.82,p\text{-value}=0.078$

This means that the two raters are equally precise.

The omnibus test of equality of the two means and the two variances is:

$Z_{mp}=0.469$ , and Q = 1.52, with p-value = 0.468, and we Therefore, we accept the hypothesis that the two raters are unbiased relative to each other and are equally precise. In addition to the fact that ${\rho }_{12}$ is quite high we may be tempted to conclude that there is strong agreement between the two raters. This conclusion is flawed since the two raters are not unbiased relative to each other.

3. Bland & Altman’s and Bradley-Blackwood (1989) Methodologies

Bradley-Blackwood [4] proposed using the F-statistic for testing the significance of the simple regression parameters in order to assess agreement between the two raters. Here we summarize their methods.

Let $y=x_1-x_2$ , and $x=\frac{1}{2}\left(x_1+x_2\right)$ .

From the multivariate normal theory, the regression of y on x is given by the conditional expectation:

$E\left[y|x\right]={\mu }_y+{\rho }_{xy}\frac{{\sigma }_y}{{\sigma }_x}\left(x-{\mu }_x\right)$ (4)

Moreover,

$\mathrm{var}\left[y|x\right]={\sigma }_y^2\left(1-{\rho }_{xy}^2\right)$ (5)

The regression Equation (4) has parameters that can be easily expressed as functions of bivariate norma parameters BVN ( $\mu ,{\mu }_2,{\sigma }_1^2,{\sigma }_2^2,{\rho }_{12}$ ) where BVN stands for bivariate normal:

Form the algebra of bivariate normal distribution we have:

$E\left(y\right)\equiv {\mu }_y={\mu }_1-{\mu }_2$

$\mathrm{var}\left(y\right)\equiv {\sigma }_y^2={\sigma }_1^2+{\sigma }_2^2-2{\rho }_{12}{\sigma }_1{\sigma }_2$

$E\left(x\right)\equiv {\mu }_x=\frac{1}{2}\left({\mu }_1+{\mu }_2\right)$

$\mathrm{var}\left(x\right)\equiv {\sigma }_x^2=\frac{1}{4}\left[{\sigma }_1^2+{\sigma }_2^2+2{\rho }_{12}{\sigma }_1{\sigma }_2\right]$ .

We can also show that the correlation between x and y is given by:

${\rho }_{xy}\equiv \text{corr}\left(x,y\right)=\frac{{\sigma }_1^2-{\sigma }_2^2}{{\left[{\left({\sigma }_1^2+{\sigma }_2^2\right)}^2-4{\rho }_{12}^2{\sigma }_1^2{\sigma }_2^2\right]}^{1/2}}$ (6)

We also note that:

$\frac{{\rho }_{xy}^2}{1-{\rho }_{xy}^2}=\frac{{\left({\sigma }_1^2-{\sigma }_2^2\right)}^2}{4{\sigma }_1^2{\sigma }_2^2\left(1-{\rho }_{12}^2\right)}$ (7)

The quantity in (7) mimics the effect size, or the non-centrality parameter which is usually used to evaluate the power of the test of significance on the regression parameters when the null hypothesis does not hold. Writing Equation (4) in a simple linear regression format we get:

$E\left[y|x\right]=\alpha +\beta \left(x-{\mu }_x\right)$ (8)

Comparing (4) and (8) we have:

$\alpha ={\mu }_1-{\mu }_2$ (9)

$\beta ={\rho }_{xy}\left[\frac{{\sigma }_y}{{\sigma }_x}\right]$ (10)

In terms of the bivariate normal population parameters we can write:

$\beta =\frac{2\left({\sigma }_1^2-{\sigma }_2^2\right){\left[{\sigma }_1^2+{\sigma }_2^2-2{\rho }_{12}{\sigma }_1{\sigma }_2\right]}^{1/2}}{{\left[{\left({\sigma }_1^2+{\sigma }_2^2\right)}^2-4{\rho }_{12}^2{\sigma }_1^2{\sigma }_2^2\right]}^{1/2}{\left[{\sigma }_1^2+{\sigma }_2^2+2{\rho }_{12}{\sigma }_1{\sigma }_2\right]}^{1/2}}$ (11)

As can be seen from (8), that the two raters are deemed unbiased relative to each other whenever:

$\alpha ={\mu }_1-{\mu }_2=0$ .

That is when the intercept of the linear regression equation is 0. From Equation (11) the slope of the regression model β is identically 0, when ${\sigma }_1^2={\sigma }_2^2$ , that is when the two raters are equally precise. Hence, testing the null hypothesis: $H_0:\mu -{\mu }_2=0\cap {\sigma }_1^2-{\sigma }_2^2=0$ , is equivalent to testing:

$H_0:\alpha =0\cap \beta =0$ (12)

We shall test this hypothesis against the general alternative:

$H_1:\alpha ={\alpha }_1\ne 0\cap \beta ={\beta }_1\ne 0$ .

The analytic expression of the statistic used to test the omnibus null hypothesis (12) is given by Equation (13) and was derived by [16] given in:

$F=\frac{n}{2{\hat{\sigma }}_y^2}\left[{\hat{\alpha }}^2+2\hat{\alpha }\hat{\beta }\bar{x}+{\hat{\beta }}^2\left(S_x^2+{\bar{x}}^2\right)\right]$ (13)

The elements of the R. H. S. of (13) are:

$S_x^2=S{S}_x/n$

${\hat{\sigma }}_y^2=\frac{1}{n-2}\left[S{S}_y-{\left(S{S}_{xy}\right)}^2/S{S}_x\right]$ (14)

$\bar{x}=\frac{1}{n}\underset{i=1}{\overset{n}{{\displaystyle \sum }}}{x}_i$

$S{S}_x=\underset{i=1}{\overset{n}{{\displaystyle \sum }}}{\left(x_i-\bar{x}\right)}^2$

$\hat{\beta }=S{S}_{xy}/S{S}_x$

$S{S}_{xy}=\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)$

and $\hat{\alpha }=\bar{y}-\hat{\beta }\bar{x}$ , where n is the sample size.

In the context of agreement between two raters Bland and Altman [2] proposed a graphical plot, whereby the horizontal axis represents the subjects mean of the two measurements taken by each of the two raters $\frac{1}{2}\left(x_1+x_2\right)$ and the vertical axis represents the difference $y=x_1-x_2$ , between the two ratings for each individual. Bartko [3] recommended that in agreement studies where measurements are reported on the continuous scale both graphical and ANOVA of regression be used as a formal test on the absence of bias of ratings and equal precision.

The null hypothesis is rejected when the test statistic:

Exceeds the critical value of the $F_{2,n-2}$ , That is $H_0$ is rejected at a significance level $\alpha$ if $F>F_{\alpha ,2,n-2}$ , where $F_{\alpha ,2,n-2}$ is the upper $\left(1-\alpha \right)100$ percentile of the $F_{2,n-2}$ distribution.

When the null hypothesis is not supported by the data, then the non-null distribution of the test statistics is that of a non-central F-distribution $\left(F_2,n-2,\lambda \right)$ with non-centrality parameter $\lambda$ , is

$\lambda =\frac{{\left({\alpha }_1+{\beta }_{1}E\left(x\right)\right)}^2+{\beta }_1^2{\sigma }_x^2}{{\sigma }_y^2}$ (15)

The elements of $\lambda$ are given by:

$\alpha ={\mu }_1-{\mu }_2$

$E\left(x\right)=\frac{1}{2}\left({\mu }_1+{\mu }_2\right)$

${\sigma }_y={\left[{\sigma }_1^2+{\sigma }_2^2-2{\rho }_{12}{\sigma }_1{\sigma }_2\right]}^{1/2}$

${\sigma }_x=\frac{1}{2}{\left[{\sigma }_1^2+{\sigma }_2^2+2{\rho }_{12}{\sigma }_1{\sigma }_2\right]}^{1/2}$ ,

and

${\beta }_1={\rho }_{xy}\frac{{\sigma }_y}{{\sigma }_x}$ .

The power of the test statistic or the probability of the false hypothesis is $1-\alpha =P_r\left[F_2,\nu ,\lambda >F_2,\nu ,\alpha \right]$ with $\nu =n-2$ being the degrees of freedom of the denominator of the F statistic.

We propose the following flowchart (Figure 1) to guide the testing of agreement.

Figure 1. The sequential approach to report continuous scale agreement results.

We illustrate the methodology using biological data given in example 1.

Example 1 continued: Unified approach to testing agreement using the ALT data:

We have two data sets of ALT measurements from the same 30 subjects. We shall use R to plot Bland and Altman levels of agreement and use ANOVA to analyze the simple linear regression of the pair-wise difference on the pair-wise average.

df=data.frame(ALT1,ALT2)

x1=as.numeric(df$ALT1)

x2=as.numeric(df$ALT2)

df=data.frame(x1,x2)

head(df)

df$x=(df$x1+df$x2)/2

df$y=df$x1-df$x2

N=nrow(df)

N

Analysis:

Step 1: Bland and Altman graphical representation (R code)

ssy=N*var(df$y)

ssy

ssxy=sum((df$x-mean(df$x))*(df$y-mean(df$y)))

ssxy

ssx=N*var(df$x)

ssx

sig=(ssy-(ssxy^2/ssx))/(N-2)

sig # residual sum of squares

library(ggplot2)

library(sadists)

df$x<-rowMeans(df)

df$y<-df$x1-df$x2

head(df)

cor(df$x,df$y)

mean_diff<-mean(df$y)

lower<-mean_diff-1.96*sd(df$y)

lower

upper<-mean_diff+1.96*sd(df$y)

upper

lower<-mean_diff-1.96*sd(df$y)

lower

upper<-mean_diff+1.96*sd(df$y)

upper

ggplot(df,aes(x=x,y=mean_diff))+

geom_point(size=5)+

geom_hline(yintercept=mean_diff)+

geom_hline(yintercept=lower, color=“red”,linetype=“dashed”)+

geom_hline(yintercept=upper, color=“red”,linetype=“dashed”)+

ggtitle(“Bland-Altman Plot”)+

ylab(“Difference Between X1 and X2”)+

xlab(“Average X1 and X2”)

From Figure 2, one may conclude that there is strong agreement between the two sets of reading since all the points fall within the limits of agreements.

Step 2: Testing for agreement using the ANOVA of regression and setting the Type I error rate at 25%.

Residual standard error: 1.032 on 28 degrees of freedom.

Anova of Regression:

Table 1 provides the results of the regression analysis produced by R, and table 2 summarizes the ANOVA results of the regression model.

Table 1. The results of the regression of the difference “y” on the pairwise mean “x”.

Table 2. The results of the ANOVA of regression.

Figure 2. Bland and Altman’s plot of the ALT dada.

The results of the hand calculation of the F-statistic and the corresponding p-value:

error=sum((df$y-predict(model_test))*(df$y-predict(model_test)))

MSE=error/(N-2)

total=sum((df$y-mean(df$y))*(df$y-mean(df$y)))

reg=total-error

MREG=reg/2

F_full model=MREG/MSE

F_full model = 1.717 which is identical to F-ANOVA/2 = 3.436/2

SSE_full model = 29.8

Error mean square = 29.8/28 = 1.113

When we use any of the statistical program available in R, SAS or SPSS, we obtain exactly the same output shown in Table 1 and Table 2. The correct value of the F statistic is 1.717. This can be verified by direct calculation of F from the analytic expression in (13).

Therefore, the F-statistic and the corresponding p-value produced by the software are not correct. We can then obtain the correct p-value using the function:

p_value=pf(1.717, 2, 28, ncp=0, lower.tail = FALSE, log.p = FALSE)

p_value= 0.198

Based on the above p-value of the global test of agreement, one may conclude that there is agreement between the two sets of ALT measurements.

However, when we examine the equality of precisions and the equality of means separately we get different conclusions. It is of interest now to see if the two methods are equally precise.

That is we would like to test the hypothesis $H_{01}:{\sigma }_1^2={\sigma }_2^2$ , or equivalently:

$H_{01}:\beta =0$ .

To test this hypothesis, we fit a regression model, without intercept, where the dependent variable is the difference (y) and the independent variable is the mean of two observations per subject (x). The R code to fit a linear model without intercept is given as:

model_noint=lm(df$y~0+df$x,data=df)

summary(model_noint)

The R-output of the regression model without intercept:

Analysis of Variance Table

Residual standard error: 1.586 on 29 degrees of freedom. From the ANOVA table, the F-statistic: 12.32 on 1 and 29 DF, p-value: 0.001483.

We need to pay close attention to the results of Table 3 and Table 4. Analytically, the residuals sum of squares carries 28 degrees of freedom not 29 as was given by the R-output. Hence the Residual mean square = 72.986/28 = 2.6066. This means the F-statistic and the corresponding p-values are not correct. Therefore, the Residual mean square is 2.6066, and the F-statistic = 31.042/2.6066 = 11.898. Consequently the p-value of the ANOVA test on the hypothesis of equality of precisions is:

p_value=pf(11.898, 1, 28, ncp=0, lower.tail = FALSE, log.p = FALSE).

p_value= 0.0018. We conclude then that the two methods are not equally precise.

We now proceed to test the hypothesis that the two methods are unbiased relative to each other. That is to test $H_{02}:\mu -{\mu }_2=0$ , or equivalently to test $H_{02}:\alpha =0$ . We use R to test for the significance of the intercept, using a regression model that does not have a slope parameter:

model_noslo=lm(df$y~1,data=df)

summary(model_noslo)

anova(model_noslo)

anova(model_noslo)

Table 3. The output of the regression model without intercept coefficient.

Table 4. ANOVA of the regression model that has no intercept parameter.

The results of Table 5 and Table 6 need to be adjusted. We note that the residual degrees of freedom produced by either R or SAS are wrong and they are supposed to be (n − 2 = 28). Moreover, the results of this test cannot be accepted because the program fails to produce F-statistic. This was also the case when we used the SAS program.

It is recommended to test the hypotheses of the absence of relative bias using the paired t-test on the original data (x₁, x₂).

PAIRED-T-TEST as an alternative to testing of relative unbiasedness:

t = −7.5692, df = 30, p-value = 1.934e−08.

Alternative hypothesis: the true mean difference is not equal to 0.

95 percent confidence interval:

−1.884241 −1.083501.

That is the two raters are not unbiased relative to each other. Similar to the results of Wilk’s asymptotic test.

As we can see there is a contradiction between the results based on the omnibus test, where the agreement was confirmed and the results based on the individual tests on the components of agreements. However, this contradiction can be resolved if we a-priori declare that agreement is declared if the p-value of the omnibus F-statistic exceeds 25%.

Example 2: Agreement between two sets of “Area under receiver operating characteristics” AUROC:

Accurate diagnosis of a disease is in many situations the first step toward its therapy. The performance of a diagnostic test is commonly compared to an infallible or reference test usually called a “gold standard”, then measured by a pair of indices such as sensitivity (Se) and specificity (Sp). Sensitivity is defined as the probability of testing positive given a person is diseased, and specificity is defined as the probability of testing negative given a person is disease-free. Other frequently used indices include positive and negative predictive values (PPV and NPV), and positive and negative diagnostic likelihood ratios (LR+ and LR−). PPV is defined as the probability of being diseased given a positive index test result, and NPV is defined as the probability of being disease-free given a negative index test result. An important measure of diagnostic accuracy which combines both sensitivity and specificity is the Area under the Receiver Operating Characteristics curve, (AUROC).

Table 5. Fitting linear regression model without slope parameter.

Table 6. Analysis of variance Table of the linear model without slope parameter.

One of the diagnostic tools that we intend to measure diagnostic accuracies combined with various studies is the FibroScan. Fibroscan is the name of a medical device used to help determine the health of a patient’s liver. The term FibroScan, which is often confused for “fiber scan,” “fibro scan” or even “fibro liver scan,” is also used to refer to the FibroScan liver test itself. If the physician is recommending a FibroScan of the liver, the likely reason is to assess the health of the liver and detect liver fibrosis, which can indicate the presence and extent of liver damage or liver disease. FibroScan uses advanced ultrasound technology called transient elastography to measure liver stiffness.

The diagnostic accuracy parameters of the non-invasive tests were estimated by comparison with liver biopsy used as the gold standard. Our aim here is to provide a methodology to confirm the agreement between the set of AUROC reported in 2006 to that reported in 2008 [17] [18] .

One should note that the measurements are in the interval $x\in \left(0,1\right)$ . To analyze this type of data it is recommended to start by applying a variance stabilizing transformation. For this type of data, the commonly used transformation is the $u={\sin }^{-1}\left(\sqrt{x}\right)$ . In this case, var(u) = ¼. This means that, for this type of data and after applying the variance stabilizing transformation the two raters are deemed to be equally precise. We also recommend that if the data are reported as count, the square root transformation should be applied to the data in order to stabilize the variance.

The summary statistics of the transformed data given in Table 7 are:

mean(AUROC_a) =0.969, var(AUROC_a)= 0.041.

mean(AUROC_b) = 0.971, var(AUROC_b) = 0.044, and cor(AUROC_a,AUROC_b)= 0.988

In Figure 3, we show the Bland-Altman plot.

R-code:

model1<-lm(df$diff~df$avg,data=df)

summary(model1)

The results of the omnibus tests are given in Table 8 and Table 9. The actual F statistic is 1.175/2 = 0.587. To find the correct p-value we use R:

p_value=pf(0.587, 2, 18, ncp=0, lower.tail = FALSE, log.p = FALSE) = 0.566

Table 7. Data of the AUROC.

Figure 3. Bland and Altman plot for the AUROC data.

Table 8. Regression output for the AUROC dada.

Table 9. Analysis of Variance of the regression model table given in Table 8.

Therefore, we may conclude that there is agreement between the two sets of ratings since the p-value exceeds the 0.25.

## MODEL NO INTERCEPT: Test for equality of precisions.

model2<-lm(df$diff~0+df$avg,data=df)

summary(model2)

anova(model2)

lm(formula = df$diff ~ 0 + df$avg, data = df)

Again, we must caution against using the residual degrees of freedom as given in R output. The correct degrees of freedom are in fact = 18. Therefore, the F statistic has F distribution with numerator and denominator degrees of freedom (1, 18), and not as shown in Table 10 and Table 11. Hence the correct p-value is obtained using the following R code.

Table 10. Output of model without intercept to test equality of precisions.

Table 11. The ANOVA table for the model without intercept.

p_value=pf(0.2894, 1, 18, ncp=0, lower.tail = FALSE, log.p = FALSE) = 0.597.

The equality of variances should come as no surprise since the variance stabilizing transformation produced constant variance = 1/4 for both raters.

Similar to example 1, the ANOVA analysis of the regression without slope does not produce F statistics which are shown in Table 12 and Table 13. We can test the equality of means of two sets of measurements using the paired t-test:

t.test(A,B, paired=TRUE)

Paired t-test results are summarized as follows:

t = −0.32361, df = 19, p-value = 0.7498, alternative hypothesis: true mean difference is not equal to 0. The 95 percent confidence interval (−0.01779321, 0.01302792) with mean difference = −0.002382647.

Note that the p-value associated with the paired t-test is identical to the p-value produced by the regression model without slope.

Other asymptotic tests for equality of precision and absence of relative bias:

Let SSE_s define the residuals sum of squares at the model with no slope, SSE_i to define the residuals sum of squares at the model with no intercept, and SSE_g to define the residuals sum of squares for the full regression model. We can avoid the incorrect assignment of degrees of freedom by the software and use an asymptotic approach suggested in [19] . If we define the two tests as:

Test_1(testing of equal precision):

Q1= n.[Log(SSE_s) - Log(SSE_g)] ≥ chis-square(1,1-α),

then we reject the hypothesis of equal precision.

Test_2 (testing of no interrater bias):

Q2= n.[ Log(SSE_i) - Log(SSE_g)] ≥ chis-square(1,1-α),

then we reject the hypothesis of absence of bias

The results of the three models are summarized in the following table.

Full model No intercept (test of equal precision) No slope (test of unbiasedness):

$SS{E}_g=0.0193$ $SS{E}_s=0.0204$ $SS{E}_i=0.0206$

For the AUROC data, Q1 = 1.1086, and Q2 = 1.3037. The Chis-square(1,1-α) = 3.8414.

Table 12. Model without slope to test of absence of bias.

Table 13. ANOVA of the regression.

Therefore, we reach to the same conclusions that both raters have equal precision, and they are unbiased relative to each other. In other words, there is high agreement between the two raters.

The issue of sample size within the context of agreement

At the early stage of designing any clinical investigation one has to decide on the number of subjects to enroll in the study to ensure validity and generalizability. In this section we shall use the R package to find estimates of the sample sizes for the three situations discussed.

1) Sample size estimation to test the null hypothesis: $H_0:\alpha =0\cap \beta =0$ against the general alternative hypothesis: $H_1:\alpha ={\alpha }_1\ne 0\cap \beta ={\beta }_1\ne 0$ .

We shall base the estimation on the usage of the ANOVA F-statistic. We use the R function (pwr.f2.test) which requires specifying the Type I error rate, the power, the numerator degrees of freedom of the F-statistic (u = 2), and the value of the non-centrality parameter λ given in (15) which is denoted by f2 in the R language. Cohen [20] demonstrated that the sample size needed for regression analysis depends on the chosen value of λ, which depends on the non-null values of the regression parameters. Values of λ around 20, are considered low, 35 is medium, and 50 is considered high.

Using the results of the AUROC example as the values for the regression parameters, we get f2 = 0.232. We force the degrees of freedom of the numerator of the F-statistic u to be equal to 2. Therefore, for type I error rate =0.05, and power 0.80, we can use the function “pwr.f2.test” to determine the number of degrees of freedom of the denominator of the F-statistic v. Since the sample size = denominator degrees of freedom +2, we get the following results:

library (pwr)

pwr.f2.test(u=2, f2=0.232, sig.level=0.05, power=0.80)

u = 2 (numerator degrees of freedom of the F statistic)

v = n - 2 = 41.66 (denominator degrees of freedom of the F-statistic)

Hence, sample size n= round(v) + 2 = 44.

2) Sample size requirements for testing equality of precisions, or testing the null hypothesis $H_0:{\sigma }_1^2={\sigma }_2^2$ , or equivalently $H_{01}:\beta =0$ , (see Equation (11)), against the general alternative:

.

Note that to test the equality of precision we used the F-statistic of the ANOVA of the regression model without intercept. The numerator degrees of freedom are u = 1, and the denominator degrees of freedom are v = n - 2. If we arbitrarily select the effect size or the non-centrality parameter f2 = 0.20, the R-code for sample size is therefore:

pwr.f2.test(u=1, f2=0.2, sig.level=0.05, power=0.80).

We get v = 39.25602. Hence the sample size is:

.

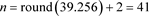3) Sample size requirement to test the absence of bias.

As we have indicated, to test the hypothesis that the two raters are unbiased relative to each other is equivalent to testing against.

We indicated that the ANOVA regression does not produce F-statistic, we tested the equality of correlated means using the paired t-test. The R function can still be used under different parameters set-up. For example, the meaning difference that we need to detect is denoted by “d”. Therefore, for power = 0.80, and level of significance = 0.05, the code is:

pwr.t.test(d=.2,power=0.8,sig.level=0.05,type=“paired”,alternative=“two.sided”)

n = 198, which is the number of required subjects or a number of pairs.

4. Discussion

Statistical analyses of measurement of the agreement are presented both graphically and analytically There is a great deal of research on the subject of agreement, but to our knowledge, there is no document focusing on a unified approach to the numerical evaluations and reporting of agreement studies in the medical field [21] [22] . The fundamental aim of our research was to provide a unified and robust approach to properly estimate and test agreements within healthcare settings. It is not out of place to mention that Hayes et al. [16] claimed that the omnibus F-statistic reported in the ANOVA of the regression model which has a numerator and denominator degrees of freedom given respectively as (2, n − 2) is the average of the two F-statistics each with (1, n − 2) degrees of freedom. Due to lack of mathematical rigor we did not use their results.

5. Conclusion

We have proposed specific guidelines to report the results of testing related to agreement studies. The guidelines are broadly useful and applicable to most diagnostic issues. To properly report the results, the user may use standard statistical packages such as SAS, R, and SPSS. However, proper adjustment to the results reported by the packages is needed. We have outlined the appropriate techniques to ascertain the agreement of paired numerical data sets when assessing agreement is the subject of interest. We also provided two worked examples to illustrate these techniques, and we also provided the complete R [23] codes which may be readily used for data analyses of similar studies.

Acknowledgements

The author acknowledges the constructive comments made by anonymous reviewers.

Conflicts of Interest

None declared by the author.

References

[1]	Bland, J.M. and Altman, D.G. (1986) Statistical Methods for Assessing Agreement between Two Methods of Clinical Measurement. The Lancet, 327, 307-310. https://doi.org/10.1016/S0140-6736(86)90837-8
[2]	Bland, J.M. and Altman, D.G. (1995) Comparing Methods of Measurement: Why Plotting Difference against Standard Method Is Misleading. The Lancet, 346, 1085-1087. https://doi.org/10.1016/S0140-6736(95)91748-9
[3]	Bartko, J.J. (1994) Measures of Agreement: A Single Procedure. Statistics in Medicine, 13, 737-745. https://doi.org/10.1002/sim.4780130534
[4]	Bradley, E.L. and Blackwood, L.G. (1989) Comparing Paired Data: A Simultaneous Test for Means and Variances. The American Statistician, 43, 234-235. https://doi.org/10.1080/00031305.1989.10475665
[5]	Stephenson, J.M. and Babiker, A. (2000) Overview of Study Design in Clinical Epidemiology. Sexually Transmitted Infections, 76, 244-247. https://doi.org/10.1136/sti.76.4.244
[6]	Last, J.M. (1988) What Is “Clinical Epidemiology”? Journal of Public Health Policy, 9, 159-163. https://doi.org/10.2307/3343001
[7]	Sackett, D.L. (2002) Clinical Epidemiology. Journal of Clinical Epidemiology, 55, 1161-1166. https://doi.org/10.1016/S0895-4356(02)00521-8
[8]	Spitzer, W.O. (1986) Clinical Epidemiology. Journal of Chronic Diseases, 39, 411-415. https://doi.org/10.1016/0021-9681(86)90107-4
[9]	Kottner, J., et al. (2011) Guidelines for Reporting Reliability and Agreement Studies (GRRAS). Journal of Clinical Epidemiology, 64, 96-106. https://doi.org/10.1016/j.jclinepi.2010.03.002
[10]	Morgan, W.A. (1939) A Test for the Significance of the Difference between Two Variances in a Sample from a Normal Bivariate Population. Biometrika, 31, 13-19. https://doi.org/10.1093/biomet/31.1-2.13
[11]	Pitman, E.J.G. (1939) A Note on Normal Correlation. Biometrika, 31, 9-12. https://doi.org/10.1093/biomet/31.1-2.9
[12]	Gulliksen, H. and Wilks, S.S. (1950) Regression Tests for Several Samples. Psychometrika, 15, 91-114. https://doi.org/10.1007/BF02289195
[13]	Lazo, M. and Clark, J.M. (2008) The Epidemiology of Nonalcoholic Fatty Liver Disease: A Global Perspective. Seminars in Liver Disease, 28, 339-350. https://doi.org/10.1055/s-0028-1091978
[14]	Prati, D., Taioli, E., Zanella, A., Della Torre, E., Butelli, S., Del Vecchio, E. and Conte, D. (2002) Updated Definitions of Healthy Ranges for Serum Alanine Aminotransferase Levels. Annals of Internal Medicine, 137, 1-10. https://doi.org/10.7326/0003-4819-137-1-200207020-00006
[15]	Sanai, F.M., Helmy, A., Dale, C., Al-Ashgar, H., Abdo, A.A., Katada, K. and Hashem, A. (2011) Updated Thresholds for Alanine Aminotransferase Do Not Exclude Significant Histological Disease in Chronic Hepatitis C. Liver International, 31, 1039-1046. https://doi.org/10.1111/j.1478-3231.2011.02551.x
[16]	Hayes, K., O’Brian, K. and Kinsella, A. (2017) A Decomposition of the Bradley-Blackwood Paired-Samples Omnibus Test. Communications in Statistics-Theory and Methods, 46, 9892-9896. https://doi.org/10.1080/03610926.2016.1222439
[17]	Friedrich-Rust, M., Ong, M.F., Martens, S., Sarrazin, C., Bojunga, J., Zeuzem, S. and Herrmann, E. (2008) Performance of Transient Elastography for the Staging of Liver Fibrosis: A Meta-Analysis. Gastroenterology, 134, 960-974. https://doi.org/10.1053/j.gastro.2008.01.034
[18]	Friedrich-Rust, M., Rosenberg, W., Parkes, J., Herrmann, E., Zeuzem, S. and Sarrazin, C. (2010) Comparison of ELF, FibroTest and FibroScan for the Non-Invasive Assessment of Liver Fibrosis. BMC Gastroenterology, 10, Article No. 103. https://doi.org/10.1186/1471-230X-10-103
[19]	Carroll, R.J. and Ruppert, D. (1988) Transformation and Weighting in Regression. Chapman and Hall, New York. https://doi.org/10.1007/978-1-4899-2873-3
[20]	Cohen, J. (1992) A Power Primer. Psychological Bulletin, 112, 155-159. https://doi.org/10.1037/0033-2909.112.1.155
[21]	Shoukri, M.M. (2010) Measures of Interobserver Agreement and Reliability. 2nd Edition, Chapman & Hall/CRC, Boca Raton. https://doi.org/10.1201/b10433
[22]	Shoukri, M.M. (2015) Agreement. Encyclopedia of Biostatistics. Wiley, New York.
[23]	https://cran.r-project.org/bin/windows/base/