Collatz Iterative Trajectories of All Odd Numbers Attain Bounded Values

Jinqing Zhang¹, Xintong Zhang²

¹Beijing, China.
²Toronto, Canada.

DOI: 10.4236/jamp.2023.1110200                

Abstract

The aim of this paper is to study the 3x + 1 problem based on the Collatz iterative formula. It can be seen from the iterative formula that the necessary condition for the Collatz iteration convergence is that its slope being less than 1. An odd number N that satisfies the condition of a slope less than 1 after n^th Collatz iterations is defined as an n-step odd number. Through statistical analysis, it is found that after n^th Collatz iterations, the iterative value of any n-step odd number N that is greater than 1 is less than N, which proves that the slope less than 1 is a sufficient and necessary condition for Collatz iteration convergence.

Keywords

Number Theory, 3x + 1 Problem, Collatz Conjecture, Syracuse Problem, Statistical Analysis

1. Introduction

The 3x + 1 problem, also known as the “Collatz conjecture” or the “Syracuse problem”, is an interesting topic. It is easy to understand, but not yet proved. The 3x + 1 problem has attracted many mathematic lovers including famous scholars [1] - [7] . The problem can be described as follows: Take any odd number, multiply it by 3 and add 1 to make it an even number, divide it by the power of 2 to make it an odd number, and repeat the arithmetic operation, the final result must be 1. The 3x + 1 problem can also be written as: Take any odd number greater than 1, multiply it by 3 and add 1 to make it an even number, divide it by the power of 2 to make it an odd number, and repeat the arithmetic operation, the final result must be less than the original odd number. Documents [1] and [2]

have proved that the necessary condition for $C_n\left(N\right)<N$ is $m=\mathrm{int}\left(n\frac{\log 3}{\log 2}+1\right)$ and also proved that when $m=\mathrm{int}\left(n\frac{\log 3}{\log 2}+1\right)$ , there are many odd numbers that are also convergent, that is, $C_n\left(N\right)<N$ , but it has not been proven that all odd numbers are convergent. This paper is based on the Collatz iterative formula $C_n\left(N\right)=\frac{3^n}{2^m}N+S_n\left(N\right)$ , through the change patterns of $\log \left[\frac{2^m{S}_n\left(N\right)}{\left(2^m-3^n\right)N}\right]$ towards $\log \left(\frac{2^m-3^n}{3^n}N\right)$ , to prove Collatz iteration convergence, that is, the necessary and sufficient condition for $C_n\left(N\right)<N$ is $m=\mathrm{int}\left(n\frac{\log 3}{\log 2}+1\right)$ .

2. Collatz Iterative Formula

For any odd number N, multiply by 3 and add 1 to make it an even number is called an odd transformation, and divide by the power of 2 to make it an odd number is called an even transformation. This process can be called an odd-even transformation.

The Collatz algorithm of an odd-even transformation can be written as:

$C_1\left(N\right)=\frac{3N+1}{2^{m_1}}=\frac{3}{2^{m_1}}N+S_1\left(N\right)$ (1.1)

$S_1\left(N\right)=\frac{1}{2^{m_1}}$ (1.2)

The Collatz algorithm of 2^nd odd-even transformations can be written as:

$C_2\left(N\right)=\frac{3C_1\left(N\right)+1}{2^{m_2}}=\frac{3^2}{2^{m_2+m_1}}N+S_2\left(N\right)$ (1.3)

$S_2\left(N\right)=\frac{3S_1\left(N\right)+1}{2^{m_2}}=\frac{3^{2-1}+2^{m_1}}{2^{m_2+m_1}}$ (1.4)

The Collatz algorithm of 3^rd odd-even transformations can be written as:

$C_3\left(N\right)=\frac{3C_2\left(N\right)+1}{2^{m_3}}=\frac{3^3}{2^{m_3+m_2+m_1}}N+S_3\left(N\right)$ (1.5)

$S_3\left(N\right)=\frac{3S_2\left(N\right)+1}{2^{m_3}}=\frac{3^{3-1}+3^{3-2}{2}^{m_1}+2^{m_2+m_1}}{2^{m_3+m_2+m_1}}$ (1.6)

Thus, the Collatz algorithm of n^th odd-even transformations can be written as:

$C_n\left(N\right)=\frac{3^n}{2^{m_n+m_{n-1}+\cdots +m_2+m_1}}N+S_n\left(N\right)$ (1.7)

$S_n\left(N\right)=\frac{3^{n-1}+3^{n-2}{2}^{m_1}+3^{n-3}{2}^{m_2+m_1}+\cdots +3^1{2}^{m_{n-2}+\cdots +m_2+m_1}+2^{m_{n-1}+\cdots +m_2+m_1}}{2^{m_n+m_{n-1}+\cdots +m_2+m_1}}$ (1.8)

Adopt the summation notation [3] :

$m={\displaystyle {\sum }_{i=1}^n{m}_i}$ (1.9)

$m_{\left[1,k\right]}={\displaystyle {\sum }_{i=1}^k{m}_i}\left(1<k<n\right)$ (1.10)

$m_i$ is the number of times of even transformations with regards to the i^th odd transformations, m is the accumulative number of times of even transformations.

So (1.7) can be written as:

$C_n\left(N\right)=\frac{3^n}{2^m}N+S_n\left(N\right)$ (1.11)

$\frac{3^n}{2^m}$ is the slope of the Collatz iterative formula, $S_n\left(N\right)$ is the intercept of the Collatz iterative formula.

And (1.8) can be written as:

$S_n\left(N\right)=\frac{3^{n-1}+3^{n-2}{2}^{m_1}+3^{n-3}{2}^{m_{\left[1,2\right]}}+\cdots +3^1{2}^{m_{\left[1,n-2\right]}}+2^{m_{\left[1,n-1\right]}}}{2^m}$ (1.12)

3. Necessary Conditions for Collatz Iteration Convergence

3.1. Necessary Conditions and the Definition of n-Step Odd Number

Define $D_n\left(N\right)$ as follows:

$D_n\left(N\right)=N-C_n\left(N\right)$ (2.1)

Substitute Equation (1.11) into Equation (2.1) we can get:

$D_n\left(N\right)=\frac{2^m-3^n}{2^m}N-S_n\left(N\right)$ (2.2)

Since $S_n\left(N\right)>0$ , then the necessary condition for $D_n\left(N\right)\ge 0$ is [2] :

$2^m-3^n>0$ (2.3)

which is, the slope $\frac{3^n}{2^m}$ is less than 1.

From Equation (2.3) it can be obtained that:

$m>n\frac{\log 3}{\log 2}$ (2.4)

Mark the smallest m that satisfies (2.4) as:

$m=\mathrm{int}\left(n\frac{\log 3}{\log 2}+1\right)$ (2.5)

Then it can be found that when $m<\mathrm{int}\left(n\frac{\log 3}{\log 2}+1\right)$ , the odd number N will not

fall into a cycle. If an odd number does not fall into a cycle during the odd and even transformation process, then after n times of odd transformations, m times of even transformations will eventually occur, making Equation (2.5) true [4] .

The odd number N that satisfies Equation (2.5) is called n-step odd number.

Define $\epsilon$ as follows:

$\epsilon =m-n\frac{\log 3}{\log 2}=\mathrm{int}\left(n\frac{\log 3}{\log 2}+1\right)-n\frac{\log 3}{\log 2}$ (2.6)

$\epsilon$ is a function of n, and its value is greater than 0 and less than 1. The relationship between $m,\epsilon$ and n is shown in Table 1.

Table 1. The relationships among $m,\epsilon ,S_n{\left(N\right)}_{\min },S_n{\left(N\right)}_{\max }$ and n.

3.2. Collatz Iterative Trajectory Vector

In the Collatz iterative trajectory sequence $\left\{C_1\left(N\right),C_2\left(N\right),\cdots ,C_{n-1}\left(N\right),C_n\left(N\right)\right\}$ of n-step odd number N, $C_1\left(N\right),C_2\left(N\right),\cdots ,C_{n-1}\left(N\right)$ are all odd numbers, and $C_n\left(N\right)$ may be an odd number or an even number.

$\left(m_1,m_2,\cdots ,m_n\right)$ which correspond to the Collatz iterative trajectory sequence is called the Collatz iterative trajectory vector of n-step odd number N, where $m_1,m_2,\cdots ,m_{n-1}\ge 1$ and $m_n\ge 2$ .

It can be seen that:

The number of types of 1-step odd number less than 2² is 1, and the Collatz iterative trajectory vector is:

(2)

The number of types of 2-step odd number less than 2⁴ is 1, and the Collatz iterative trajectory vector is:

(1, 3)

The number of types of 3-step odd numbers less than 2⁵ is 2, and the Collatz iterative trajectory vectors are:

(1, 1, 3)

(1, 2, 2)

The number of types of 4-step odd numbers less than 2⁷ is 3, and the Collatz iterative trajectory vectors are:

(1, 1, 1, 4)

(1, 1, 2, 3)

(1, 2, 1, 3)

The number of types of 5-step odd numbers less than 2⁸ is 7, and the Collatz iterative trajectory vectors are:

(1, 1, 1, 1, 4)

(1, 1, 1, 2, 3)

(1, 1, 1, 3, 2)

(1, 1, 2, 1, 3)

(1, 1, 2, 2, 2)

(1, 2, 1, 1, 3)

(1, 2, 1, 2, 2)

The number of types of 6-step odd numbers less than 2¹⁰ is 12, and the Collatz iterative trajectory vectors are:

(1, 1, 1, 1, 1, 5)

(1, 1, 1, 1, 2, 4)

(1, 1, 1, 1, 3, 3)

(1, 1, 1, 2, 1, 4)

(1, 1, 1, 2, 2, 3)

(1, 1, 1, 3, 1, 3)

(1, 1, 2, 1, 1, 4)

(1, 1, 2, 1, 2, 3)

(1, 1, 2, 2, 1, 3)

(1, 2, 1, 1, 1, 4)

(1, 2, 1, 1, 2, 3)

(1, 2, 1, 2, 1, 3)

By analogy, all odd-numbered Collatz iterative trajectory vectors of any number of steps can be constructed.

Assume that the number of n-step odd numbers less than $2^{\mathrm{int}\left(n\frac{\log 3}{\log 2}+1\right)}$ is q, and its vector is: $\left(m_{j1},m_{j2},\cdots ,m_{jn}\right)$ $j=1,2,\cdots ,q$ , then the number of n + 1-step odd numbers less than $2^{\mathrm{int}\left(\left(n+1\right)\frac{\log 3}{\log 2}+1\right)}$ is ${\displaystyle {\sum }_{j=1}^q{m}_{jn}}-q$ .

3.3. The Maximum and Minimum Values of S_n(N) and Their Relationships to n

By substituting the Collatz iterative trajectory vector components of n-step odd numbers into Equation (1.12), the $S_n\left(N\right)$ values of n-step odd numbers can be calculated.

1-step odd numbers can be represented by $2^{2}x+1$ , and their $S_n\left(N\right)$ value is:

$S_1\left(2^{2}x+1\right)=\frac{3^{1-1}}{2^2}=0.25$ (2.7)

Note x is a non-negative integer.

2-step odd numbers can be represented by $2^{4}x+3$ , and their $S_n\left(N\right)$ value is:

$S_2\left(2^{4}x+3\right)=\frac{3^{2-1}+2^1}{2^4}=0.3125$ (2.8)

3-step odd numbers can be represented by $2^{5}x+23$ or $2^{5}x+11$ , and their $S_n\left(N\right)$ values are:

$S_3\left(2^{5}x+23\right)=\frac{3^{3-1}+3^{3-2}{2}^1+2^2}{2^5}=0.59375$ (2.9)

$S_3\left(2^{5}x+11\right)=\frac{3^{3-1}+3^{3-2}{2}^1+2^3}{2^5}=0.71875$ (2.10)

4-step odd numbers can be represented by $2^{7}x+15$ , $2^{7}x+7$ , or $2^{7}x+59$ , and their $S_n\left(N\right)$ values are:

$S_4\left(2^{7}x+15\right)=\frac{3^{4-1}+3^{4-2}{2}^1+3^{4-3}{2}^2+2^3}{2^7}=0.50781$ (2.11)

$S_4\left(2^{7}x+7\right)=\frac{3^{4-1}+3^{4-2}{2}^1+3^{4-3}{2}^2+2^4}{2^7}=0.57031$ (2.12)

$S_4\left(2^{7}x+59\right)=\frac{3^{4-1}+3^{4-2}{2}^1+3^{4-3}{2}^3+2^4}{2^7}=0.66406$ (2.13)

5-step odd numbers can be represented by $2^{8}x+95$ , $2^{8}x+175$ , $2^{8}x+39$ , $2^{8}x+79$ , $2^{8}x+199$ , $2^{8}x+219$ or $2^{8}x+123$ , and their $S_n\left(N\right)$ values are:

$S_5\left(2^{8}x+95\right)=\frac{3^{5-1}+3^{5-2}{2}^1+3^{5-3}{2}^2+3^{5-4}{2}^3+2^4}{2^8}=0.82422$ (2.14)

$S_5\left(2^{8}x+175\right)=\frac{3^{5-1}+3^{5-2}{2}^1+3^{5-3}{2}^2+3^{5-4}{2}^3+2^5}{2^8}=0.88672$ (2.15)

$S_5\left(2^{8}x+39\right)=\frac{3^{5-1}+3^{5-2}{2}^1+3^{5-3}{2}^2+3^{5-4}{2}^4+2^5}{2^8}=0.98047$ (2.16)

$S_5\left(2^{8}x+79\right)=\frac{3^{5-1}+3^{5-2}{2}^1+3^{5-3}{2}^2+3^{5-4}{2}^3+2^6}{2^8}=1.01172$ (2.17)

$S_5\left(2^{8}x+199\right)=\frac{3^{5-1}+3^{5-2}{2}^1+3^{5-3}{2}^2+3^{5-4}{2}^4+2^6}{2^8}=1.11547$ (2.18)

$S_5\left(2^{8}x+219\right)=\frac{3^{5-1}+3^{5-2}{2}^1+3^{5-3}{2}^3+3^{5-4}{2}^4+2^5}{2^8}=1.12109$ (2.19)

$S_5\left(2^{8}x+123\right)=\frac{3^{5-1}+3^{5-2}{2}^1+3^{5-3}{2}^3+3^{5-4}{2}^4+2^6}{2^8}=1.24609$ (2.20)

It can be seen that there are multiple odd numbers that are equal to or greater than 3-step odd number. For the same step but different types of odd number, their $S_n\left(N\right)$ values are different, with $S_n\left(N\right)$ minimum value and maximum value exist.

From Equation (1.12), we can see that when the first $n-1$ components of the Collatz iterative trajectory vector are 1, and the last component is $m-n+1$ , that is, the trajectory vector of the n-step odd number is $\left(1,1,\cdots ,1,m-n+1\right)$ then $S_n\left(N\right)$ has the minimum value. Substitute the trajectory vector components into Equation (1.12), we can get:

$\begin{array}{c}{S}_n{\left(N\right)}_{\min }=\frac{3^{n-1}+3^{n-2}{2}^1+3^{n-3}{2}^2+\cdots +3^1{2}^{n-2}+2^{n-1}}{2^m}\\ =\frac{{\left(\frac{3}{2}\right)}^{n-1}+{\left(\frac{3}{2}\right)}^{n-2}+\cdots +\frac{3}{2}+1}{2^{m-n+1}}=\frac{3^n-2^n}{2^m}\end{array}$ (2.21)

Based on the value of n, Equation (2.5), and Equation (2.21), $S_n{\left(N\right)}_{\min }$ of n-step odd numbers can be calculated. Refer to Table 1.

Based on Equation (2.6), Equation (2.21) can be written as:

$S_n{\left(N\right)}_{\min }=\frac{1}{2^{\epsilon }}\left[1-{\left(\frac{2}{3}\right)}^n\right]<\frac{1}{2^{\epsilon }}<1$ (2.22)

When n is large enough, then

$S_n{\left(N\right)}_{\min }\approx \frac{1}{2^{\epsilon }}$ (2.23)

Based on Equation (1.12), the trajectory vector components of the maximum $S_n\left(N\right)$ should meet the following conditions:

$m_{\left[1,k\right]}={\displaystyle {\sum }_{i=1}^k{m}_i}=\mathrm{int}\left(k\frac{\log 3}{\log 2}\right)\left(1\le k<n,m_i=1\text{or}2\right)$ (2.24)

$m={\displaystyle {\sum }_{i=1}^n{m}_i}=\mathrm{int}\left(n\frac{\log 3}{\log 2}+1\right)\left(m_n=2\text{or}3\right)$ (2.25)

Substitute the Collatz iterative trajectory vector components that satisfy Equation (2.24) and Equation (2.25) into Equation (1.12), the $S_n{\left(N\right)}_{\max }$ can be calculated. Refer to Table 1.

According to statistics, $S_n{\left(N\right)}_{\max }$ has a good linear relationship with $\frac{n}{2^{\epsilon }}$ .

Figure 1 shows their relationship when n is in the range of 1 - 50, and Figure 2 shows their relationship when n in the range of 1 - 500. The larger the n is, the better the linear relationship is. If the value of n is small, an intercept can be added to the linear regression.

It can be seen from Figure 2.

Figure 1. The relationship between $S_n{\left(N\right)}_{\max }$ and $\frac{n}{2^{\epsilon }}$ (n is in the range of 1 to 50).

Figure 2. The relationship between $S_n{\left(N\right)}_{\max }$ and $\frac{n}{2^{\epsilon }}$ (n is in the range of 1 to 500).

$S_n{\left(N\right)}_{\max }\approx \frac{0.241n}{2^{\epsilon }}$ (2.26)

Based on (2.23), Equation (2.26) can be written as:

$\frac{S_n{\left(N\right)}_{\max }}{S_n{\left(N\right)}_{\min }}\approx 0.241n$ (2.27)

That is, the ratio of $S_n{\left(N\right)}_{\max }/S_n{\left(N\right)}_{\min }$ is approximately proportional to n.

4. Necessary and Sufficient Conditions for Collatz Iteration Convergence

4.1. n-Step Odd Number Converges When $S_n\left(N\right)=S_n{\left(N\right)}_{min}$

From Equation (2.2) we can get:

$N=\frac{2^m{D}_n\left(N\right)+2^m{S}_n{\left(N\right)}_{\min }}{2^m-3^n}$ (3.1)

Substitute Equation (2.21) into Equation (3.1) we can get:

$N=\frac{2^m{D}_n\left(N\right)+3^n-2^n}{2^m-3^n}$ (3.2)

If the iteration is divergent, that is, $D_n\left(N\right)<0$ , because $D_n\left(N\right)$ is an integer, that is, $D_n\left(N\right)\le -1$ , substitute it into Equation (3.2) we can get:

$N\le \frac{-2^m+3^n-2^n}{2^m-3^n}=-1-\frac{2^n}{2^m-3^n}<0$ (3.3)

It can be seen that $D_n\left(N\right)$ cannot be less than 0.

If the iteration is cyclic, that is, $D_n\left(N\right)=0$ , substitute it into Equation (3.2) we can get:

$\left(2^m-3^n\right)N=3^n-2^n$ (3.4)

For $S_n\left(N\right)=S_n{\left(N\right)}_{\min }$ , the n-step odd number N can be expressed as:

$N=2^{n}x-1$ (3.5)

Substitute Equation (3.5) into (3.4) and arrange it, we can get:

$\left(2^m-3^n\right)x=2^{m-n}-1$ (3.6)

It can be seen from the literature [5] that there is no other solution except $x=1,n=1,m=2$ (that is, $N=1$ ). This proves that when $S_n\left(N\right)=S_n{\left(N\right)}_{\min }$ , n-step odd number N(>1) neither diverges nor cycles. That is, for this special n-step odd number, Equation (2.5) is the necessary and sufficient condition for convergence.

4.2. n-Step Odd Number N_nmin Converges

Literature [1] has proven that n-step odd numbers N satisfy Equation (2.5), then there do exist n-step odd numbers $2^{m}x+N$ such that $C_n\left(2^{m}x+N\right)<2^{m}x+N$ . Now we first prove that for the minimum odd number $N_{n\min }$ of n-step odd numbers, the relationship $C_n\left(N_{n\min }\right)<N_{n\min }$ is established.

From Equation (2.2) we can get:

$D_n\left(N\right)=\frac{2^m-3^n}{2^m}N\left[1-\frac{2^m{S}_n\left(N\right)}{\left(2^m-3^n\right)N}\right]$ (3.7)

Substitute $N=N_{n\min }$ into the above formula to get:

$\begin{array}{c}{D}_n\left(N_{n\min }\right)=\frac{2^m-3^n}{2^m}{N}_{n\min }\left[1-\frac{2^m{S}_n\left(N_{n\min }\right)}{\left(2^m-3^n\right)N_{n\min }}\right]\\ =\frac{2^{\epsilon }-1}{2^{\epsilon }}{N}_{n\min }\left[1-\frac{2^{\epsilon }{S}_n\left(N_{n\min }\right)}{\left(2^{\epsilon }-1\right)N_{n\min }}\right]\end{array}$ (3.8)

According to Equation (2.5), the minimum odd number $N_{n\min }$ of n-step odd numbers N ( $1<N<2^{30}$ ) can be obtained. Figure 3 shows the relationship between $\log \left[\left(2^{\epsilon }-1\right)N_{n\min }\right]$ and $\log \left(N_{n\min }\right)$ . It can be seen from Figure 3 that $\log \left[\left(2^{\epsilon }-1\right)N_{n\min }\right]$ increases spirally as $\log \left(N_{n\min }\right)$ goes up.

Figure 4 shows the relationship between $\log \left[\frac{2^{\epsilon }{S}_n\left(N_{n\min }\right)}{\left(2^{\epsilon }-1\right)N_{n\min }}\right]$ and

$\log \left[\left(2^{\epsilon }-1\right)N_{n\min }\right]$ . It can be seen from Figure 4 that $\frac{2^{\epsilon }{S}_n\left(N_{n\min }\right)}{\left(2^{\epsilon }-1\right)N_{n\min }}$ is always

less than 1 and gets close to 0 as $\log \left[\left(2^{\epsilon }-1\right)N_{n\min }\right]$ increases spirally. Therefore, $D_n\left(N_{n\min }\right)$ is neither less than 0 nor equal to 0, but is always greater than 0. That is, the relationship $C_n\left(N_{n\min }\right)<N_{n\min }$ is established.

4.3. All Odd Numbers Greater Than 1 Converge

It is proved below that all odd numbers N less than 2^m satisfy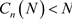. From Equation (3.7) we can get:

Figure 3. The relationship between $\log \left[\left(2^{\epsilon }-1\right)N_{n\min }\right]$ and $\log \left(N_{n\min }\right)$ ( $1<N<2^{30}$ ).

Figure 4. The relationship between $\log \left[\frac{2^{\epsilon }{S}_n\left(N_{n\min }\right)}{\left(2^{\epsilon }-1\right)N_{n\min }}\right]$ and $\log \left[\left(2^{\epsilon }-1\right)N_{n\min }\right]$ ( $1<N<2^{30}$ ).

Figure 5. The relationship between $\log \left[\frac{2^{\epsilon }{S}_n{\left(N\right)}_{\max }}{\left(2^{\epsilon }-1\right)N_{n\min }}\right]$ and $\log \left[\left(2^{\epsilon }-1\right)N_{n\min }\right]$ ( $1<N<2^{30}$ ).

$D_n\left(N\right)=\frac{2^m-3^n}{2^m}N\left[1-\frac{2^{\epsilon }{S}_n\left(N\right)}{\left(2^{\epsilon }-1\right)N}\right]\ge \frac{2^m-3^n}{2^m}N\left[1-\frac{2^{\epsilon }{S}_n{\left(N\right)}_{\max }}{\left(2^{\epsilon }-1\right)N_{n\min }}\right]$ (3.9)

According to Equation (2.24), Equation (2.25) and Equation (2.5), the maximum value $S_n{\left(N\right)}_{\max }$ of n-step odd number can be calculated. Figure 5 shows

the relationship between $\log \left[\frac{2^{\epsilon }{S}_n{\left(N\right)}_{\max }}{\left(2^{\epsilon }-1\right)N_{n\min }}\right]$ and $\log \left[\left(2^{\epsilon }-1\right)N_{n\min }\right]$ .

As depicted in Figure 5, only when $n=34,N_{34\min }=47$ and

$n=37,N_{37\min }=27$ , $\log \left[\frac{2^{\epsilon }{S}_n{\left(N\right)}_{\max }}{\left(2^{\epsilon }-1\right)N_{n\min }}\right]>0$ , that is, $\frac{2^{\epsilon }{S}_n{\left(N\right)}_{\max }}{\left(2^{\epsilon }-1\right)N_{n\min }}>1$ ; in other cases, $\frac{2^{\epsilon }{S}_n{\left(N\right)}_{\max }}{\left(2^{\epsilon }-1\right)N_{n\min }}$ is always less than 1, and tends to be close to 0 as

$\log \left[\left(2^{\epsilon }-1\right)N_{n\min }\right]$ spirals up. From Section 4.2, we can see that $N_{34\min }=47$ and $N_{37\min }=27$ are convergent, which proves that $D_n\left(N\right)=N-C_n\left(N\right)>0$ for all odd numbers. Therefore, Collatz conjecture is established, and n-step odd numbers can also be called n-step convergence odd numbers.

5. Conclusions

1) For any odd number N, it will not fall into a cycle when $m<\mathrm{int}\left(n\frac{\log 3}{\log 2}+1\right)$ , then after n times of odd transformations, m times of even transformations will eventually occur, making equation $m=\mathrm{int}\left(n\frac{\log 3}{\log 2}+1\right)$ true.

2) For any odd number N that is greater than 1, $m=\mathrm{int}\left(n\frac{\log 3}{\log 2}+1\right)$ is the

necessary and sufficient condition for Collatz iteration convergence, that is, $C_n\left(N\right)<N$ .

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Terras, R. (1979) A Stopping Time Problem on the Positive Integers. Acta Arithmetica, 30, 241-252. https://doi.org/10.4064/aa-30-3-241-252
[2]	Lagarias, J.C. (1985) The 3x + 1 Problem and Its Generalizations. The American Mathematical Monthly, 92, 3-23. https://doi.org/10.2307/2322189
[3]	Tao, T. (2022) Almost All Orbits of the Collatz Map Attain Almost Bounded Values. Forum of Mathematics, Pi, 10, e12. https://doi.org/10.1017/fmp.2022.8
[4]	Hu, Z. (2021) The Analysis of Convergence for the 3X + 1 Problem and Crandall Conjecture for the aX + 1 Problem. Advances in Pure Mathematics, 11, 400-407. https://doi.org/10.4236/apm.2021.115027
[5]	Steiner, R.P. (1977) A Theorem on the Syracuse Problem. In Proceedings of the 7th Manitoba Conference on Numerical Mathematics, Vol. 29, Utilitas Mathematica Pub., Winnipeg, MB, Canada, 553-559.
[6]	Lagarias, J.C. (2003) The 3x + 1 Problem: An Annotated Bibliography (1963-1999). https://arxiv.org/abs/math/0309224
[7]	Carbó-Dorca, R. (2023) Collatz Conjecture Redefinition on Prime Numbers. Journal of Applied Mathematics and Physics, 11, 147-157. https://doi.org/10.4236/jamp.2023.111011