Bifurcation Analysis of a Nonlinear Genetic Network Model with Time Delay

Anael Verdugo

Department of Mathematics, California State University, Fullerton, USA.

DOI: 10.4236/jamp.2023.118146                

Abstract

This paper presents a bifurcation study of a mRNA-protein network with negative feedback and time delay. The network is modeled as a coupled system of N ordinary differential equations (ODEs) and N delay differential equations (DDEs). Linear analysis of the stable equilibria shows the existence of a critical time delay beyond which limit cycle oscillations are born in a Hopf bifurcation. The Poincaré-Lindstedt perturbation method is applied to the nonlinear system, resulting in closed form approximate expressions for the amplitude and frequency of oscillation. We confirm our perturbation analysis results by numerically simulating the full 2N-dimensional nonlinear system for N = 2, 7, 15, and 30. Our results show that for small perturbations the equilibrium undergoes a supercritical Hopf and the system exhibits stable periodic solutions. Furthermore, our closed form numerical expressions exhibit the importance of the network’s negative feedback and nonlinear effects.

Keywords

Bifurcation Analysis, Hopf, Delay Differential Equations

1. Introduction

The basic functions of life are carried out by millions of cells, all of which are formed of thousands of proteins and genes interacting [1] . An important goal in the areas of applied mathematics and biology is trying to understand these network of interactions. Theoretically, the network represents how certain genes affect other genes [2] and, in the case when the network involves a small number of genes, its dynamic properties can be studied directly in a laboratory [3] [4] . However, in the case when the network is formed of a large number of genes, then understanding its dynamic behavior might be difficult and nonintuitive [5] [6] . In recent years, various computational techniques have been developed that help us understand some of the intrinsic properties of these networks. For an extensive review see [7] - [14] .

The biology behind the model in this work can be roughly summarized in a three step process (see Chapter 2 for more details): 1) in the nucleus a gene is copied onto messenger RNA (mRNA), 2) the mRNA then gets translated into a protein, and 3) the protein then returns to the nucleus where it represses production of mRNA (see Figure 1). This mRNA-protein feedback mechanism has been studied previously in several works [14] [15] . One of the more promising and relevant mRNA-protein models with feedback was first studied by Monk [15] and subsequently analyzed in more detail by a few others [14] [16] .

In this work we extend the author’s previous study [14] of a single mRNA-protein model to a network formed of N coupled mRNA-protein systems. The network structure in this work is described in Section 4 and the model is given by a system of N nonlinear DDEs coupled to N linear ODEs. Section 2 gives a summary of the biological background of our model. In Section 3 we present the linear analysis of a network of two coupled mRNA-protein systems. The network of N coupled mRNA-protein systems and its associated linear analysis is presented in Section 4 followed by its nonlinear analysis in Section 5. Section 6 presents a computational analysis and comparison of MATLAB’s numerical results with our perturbation results. In Section 7 we discuss our conclusions and future directions.

2. Biological Background

Transcription and translation are the main processes by which a cell expresses the instructions encoded in its genes. Transcription is the first step in gene expression and it includes the replication of a gene into messenger RNA (mRNA). The second step is the translation process, where the mRNA diffuses out of the nucleus and is captured, read, and translated by a ribosome yielding as a final product an associated protein. The final step in this feedback mechanism happens when the protein then diffuses back into the nucleus and represses production of its own mRNA. From these mechanisms, mRNA and protein concentrations arise naturally as the main intracellular regulatory agents in our model [1] [2] .

Figure 1. Diagram of the mRNA-protein feedback inhibition mechanism. The gene is copied onto mRNA, which then diffuses out of the nucleus and gets translated into a protein. The protein then diffuses back into the nucleus where it represses the transcription of its own mRNA.

There are several mechanisms that the cell uses to regulate levels of mRNA and protein concentrations. One important mechanism is the cell’s ability to adjust and control the breakdown rate (degradation rate) of old mRNA or proteins by increasing or decreasing the concentration of enzymes that degrade these. Another important example is the cell’s ability to regulate the production rate (transcription rate) of a specific mRNA. This is usually accomplished by a special type of proteins called transcription factors, which either promote or repress mRNA production by binding directly to the gene. Although other cellular mechanisms happen parallel during this transcription-translation process, in Figure 2 we only present the main mechanisms relevant to the description of our model. Here feedback arises when the protein product returns to the nucleus as a transcription factor and slows down the transcription of its own mRNA by binding to the gene’s promoter site [3] [15] .

Previous findings [15] show that there are time delays associated with the feedback mechanism presented in Figure 2. These delays arise naturally as transcriptional delays (time it takes the gene to get copied into mRNA) and translational delays (time it takes the ribosome to translate mRNA into protein). Furthermore, recent studies [14] [15] have shown that, due to the different time scales in which these two processes occur, we can have an accurate dynamic model by considering only the transcriptional delays. As explained in [14] and [15] , the ordinary differential equations (ODEs) associated to this system are given as follows

$\frac{\text{d}m}{\text{d}t}=-{\mu }_{m}m\left(t\right)+{\alpha }_m\left(\frac{1}{1+{\left(\frac{p\left(t-T\right)}{p_0}\right)}^n}\right)$ (1)

$\frac{\text{d}p}{\text{d}t}={\alpha }_{p}m\left(t\right)-{\mu }_{p}p\left(t\right)$ (2)

where the time dependent variables are mRNA concentration, $m\left(t\right)$ , and its associated protein concentration, $p\left(t\right)$ . The constants ${\mu }_m$ and ${\mu }_p$ are the degradation rates of mRNA and protein, ${\alpha }_p$ and ${\alpha }_m$ the synthesis rates, $p_0$ is the repression threshold of protein concentration, n is the hill coefficient, and

${\left(1+{\left(\frac{p\left(t-T\right)}{p_0}\right)}^n\right)}^{-1}$ is the Hill term representing the rate of delayed mRNA synthesis, where the delay is assumed to be positive and constant, $T>0$ .

3. Linear Analysis of Two Coupled mRNA-Protein Systems

The single mRNA-protein system was studied in detail by the author in [14] . Here we present a network of two mRNA-protein systems coupled via protein repression. The protein of the first system, $p_1$ , represses production of its own mRNA, $m_1$ , and the second system’s mRNA, $m_2$ . The geometric representation

Figure 2. (a) Diagram representing the synthesis and degradation mechanisms of mRNA and protein. Solid and dashed lines represent chemical reactions and indirect regulatory signals, respectively. The synthesis and degradation rates are given by $\alpha$ and $\mu$ , respectively, and five small circles represent degradation byproducts. (b) Compact notation for the same mRNA-protein system presented in (a). Here the arrow ( $\uparrow$ ) represents production (upregulation) and the perpendicular symbol ( $\perp$ ) represents repression (downregulation).

of the network is depicted in Figure 3 and the associated 4-dimensional mathematical model is given by

${\stackrel{\dot{}}{m}}_1=-\mu m_1+\frac{1}{1+{\left(\frac{p_{1d}}{p_{10}}\right)}^n}+\frac{1}{1+{\left(\frac{p_{2d}}{p_{20}}\right)}^n}$ (3)

${\stackrel{\dot{}}{m}}_2=-\mu m_2+\frac{1}{1+{\left(\frac{p_{1d}}{p_{10}}\right)}^n}+\frac{1}{1+{\left(\frac{p_{2d}}{p_{20}}\right)}^n}$ (4)

${\stackrel{\dot{}}{p}}_1=m_1-\mu p_1$ (5)

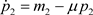(6)

where we assume $n\in \mathbb{N}$ , ${\mu }_m={\mu }_p=\mu$ , ${\alpha }_m={\alpha }_p=1$ , and $p_d=p\left(t-T\right)$ for both systems. Setting ${\mu }_m={\mu }_p=\mu$ and ${\alpha }_m={\alpha }_p=1$ sacrifices biological flexibility in regards to synthesis and degradation, but it allows us to gain mathematical and computational tractability for the analysis of the general network presented in Section 4.

Figure 3. Network diagram of two mRNA-protein systems coupled through protein repression. Protein from the first system, $p_1$ , represses its own mRNA production, $m_1$ , and the second’s system’s mRNA, $m_2$ . Each system produces it’s own protein and they all share the same degradation rates ${\mu }_m={\mu }_p=\mu$ with production rates assumed as ${\alpha }_m={\alpha }_p=1$ .

The first step in the linear analysis is to set ${\stackrel{\dot{}}{m}}_1={\stackrel{\dot{}}{m}}_2={\stackrel{\dot{}}{p}}_1={\stackrel{\dot{}}{p}}_2=0$ in (3)-(6) and find expressions for the equilibrium point $\left(m_1^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}{m}_2^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}{p}_1^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}{p}_2^{\mathrm{<mo>\; *\; </mo>}}\right)$ . We substitute the latter and eliminate $m_1^{\mathrm{<mo>\; *\; </mo>}}$ and $m_2^{\mathrm{<mo>\; *\; </mo>}}$ to obtain

${\mu }^2{p}_1^{\mathrm{<mo>\; *\; </mo>}}-\frac{1}{1+{\left(\frac{p_1^{\mathrm{<mo>\; *\; </mo>}}}{p_{10}}\right)}^n}-\frac{1}{1+{\left(\frac{p_2^{\mathrm{<mo>\; *\; </mo>}}}{p_{20}}\right)}^n}=0$ (7)

${\mu }^2{p}_2^{\mathrm{<mo>\; *\; </mo>}}-\frac{1}{1+{\left(\frac{p_1^{\mathrm{<mo>\; *\; </mo>}}}{p_{10}}\right)}^n}-\frac{1}{1+{\left(\frac{p_2^{\mathrm{<mo>\; *\; </mo>}}}{p_{20}}\right)}^n}=0$ (8)

From (7)-(8) we have that $p_1^{\mathrm{<mo>\; *\; </mo>}}=p_2^{\mathrm{<mo>\; *\; </mo>}}=p^{\mathrm{<mo>\; *\; </mo>}}$ and thus $m_1^{\mathrm{<mo>\; *\; </mo>}}=m_2^{\mathrm{<mo>\; *\; </mo>}}=\mu p^{\mathrm{<mo>\; *\; </mo>}}$ . This gives the following expression for the equilibrium solution $p^{\mathrm{<mo>\; *\; </mo>}}$

$\begin{array}{l}{\mu }^2{p}^{\mathrm{<mo>\; *\; </mo>}}{}^{2n+1}+{\mu }^2\left(p_{10}^n+p_{20}^n\right)p^{\mathrm{<mo>\; *\; </mo>}}{}^{n+1}-\left(p_{10}^n+p_{20}^n\right)p^{\mathrm{<mo>\; *\; </mo>}}{}^n\\ +{\mu }^2{\left(p_{10}{p}_{20}\right)}^n{p}^{\mathrm{<mo>\; *\; </mo>}}-2{\left(p_{10}{p}_{20}\right)}^n=0\end{array}$ (9)

which can be numerically approximated using a root finding method.

Next we define ${\xi }_1$ , ${\xi }_2$ , ${\eta }_1$ , and ${\eta }_2$ to be deviations from equilibrium: ${\xi }_1=m_1-m_1^{\mathrm{<mo>\; *\; </mo>}}$ , ${\xi }_2=m_2-m_2^{\mathrm{<mo>\; *\; </mo>}}$ , ${\eta }_1=p_1-p_1^{\mathrm{<mo>\; *\; </mo>}}$ , and ${\eta }_2=p_2-p_2^{\mathrm{<mo>\; *\; </mo>}}$ . Substituting these into (3)-(6) results

${\stackrel{\dot{}}{\xi }}_1=-\mu \left({\xi }_1+m_1^{\mathrm{<mo>\; *\; </mo>}}\right)+\frac{1}{1+{\left(\frac{{\eta }_{1d}+p_1^{\mathrm{<mo>\; *\; </mo>}}}{p_{10}}\right)}^n}+\frac{1}{1+{\left(\frac{{\eta }_{2d}+p_2^{\mathrm{<mo>\; *\; </mo>}}}{p_{20}}\right)}^n}$ (10)

${\stackrel{\dot{}}{\xi }}_2=-\mu \left({\xi }_2+m_2^{\mathrm{<mo>\; *\; </mo>}}\right)+\frac{1}{1+{\left(\frac{{\eta }_{1d}+p_1^{\mathrm{<mo>\; *\; </mo>}}}{p_{10}}\right)}^n}+\frac{1}{1+{\left(\frac{{\eta }_{2d}+p_2^{\mathrm{<mo>\; *\; </mo>}}}{p_{20}}\right)}^n}$ (11)

${\stackrel{\dot{}}{\eta }}_1={\xi }_1-\mu {\eta }_1$ (12)

${\stackrel{\dot{}}{\eta }}_2={\xi }_2-\mu {\eta }_2$ (13)

Expanding for small ${\eta }_{id}$ Equations (10)-(11) become

${\stackrel{\dot{}}{\xi }}_1=-\mu {\xi }_1+K_{11}{\eta }_{1d}+K_{21}{\eta }_{2d}+K_{12}{\eta }_{1d}^2+K_{22}{\eta }_{2d}^2+\cdots$ (14)

${\stackrel{\dot{}}{\xi }}_2=-\mu {\xi }_2+K_{11}{\eta }_{1d}+K_{21}{\eta }_{2d}+K_{12}{\eta }_{1d}^2+K_{22}{\eta }_{2d}^2+\cdots$ (15)

where $K_{ji}$ is given by

$K_{j1}=-\frac{n{\beta }_j}{{\left(1+{\beta }_j\right)}^2{p}_j^{*}}\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>},\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>}\text{where}{\beta }_j={\left(\frac{p_j^{*}}{p_{j0}}\right)}^n$ (16)

$K_{j2}=\frac{{\beta }_{j}n\left({\beta }_{j}n-n+{\beta }_j+1\right)}{2{\left({\beta }_j+1\right)}^3{p}_j^{\mathrm{<mo>\; *\; </mo>2}}}$ (17)

and thus the associated linearized system coming from Equations (12)-(15) is given by

${\stackrel{\dot{}}{\xi }}_1=-\mu {\xi }_1+K_{11}{\eta }_{1d}+K_{21}{\eta }_{2d}$ (18)

${\stackrel{\dot{}}{\xi }}_2=-\mu {\xi }_2+K_{11}{\eta }_{1d}+K_{21}{\eta }_{2d}$ (19)

${\stackrel{\dot{}}{\eta }}_1={\xi }_1-\mu {\eta }_1$ (20)

${\stackrel{\dot{}}{\eta }}_2={\xi }_2-\mu {\eta }_2$ (21)

For $T=0$ (no delay) the system (18)-(21) has the following Jacobian at the origin

$\left[\begin{array}{cccc}-\mu & 0& K_{11}& K_{21}\\ 0& -\mu & K_{11}& K_{21}\\ 1& 0& -\mu & 0\\ 0& 1& 0& -\mu \end{array}\right]$ (22)

with eigenvalues

$\left\{-\mu \mathrm{,}-\mu \mathrm{,}-\mu \pm \sqrt{K_{11}+K_{21}}\right\}$ (23)

and since $\mu >0$ and $K_{j1}<0$ then all real parts are negative and the origin is stable.

To find the critical delay, $T_{cr}$ , we assume solutions of the form ${\eta }_i=A_i{\text{e}}^{\lambda t}$ and ${\xi }_i=B_i{\text{e}}^{\lambda t}$ for $i=1,2$ and substitute into (18)-(21)

$\left(\lambda +\mu \right)B_1={\text{e}}^{-\lambda T}\left(K_{11}{A}_1+K_{21}{A}_2\right)$ (24)

$\left(\lambda +\mu \right)B_2={\text{e}}^{-\lambda T}\left(K_{11}{A}_1+K_{21}{A}_2\right)$ (25)

$\left(\lambda +\mu \right)A_1=B_1$ (26)

$\left(\lambda +\mu \right)A_2=B_2$ (27)

Substituting (26)-(27) into (24)-(25), setting $T=T_{cr}$ , and $\lambda =\text{i}\omega$ we obtain

$A_1=\frac{{\text{e}}^{-\text{i}\omega T_{cr}}}{{\left(\text{i}\omega +\mu \right)}^2}\left(K_{11}{A}_1+K_{21}{A}_2\right)$ (28)

$A_2=\frac{{\text{e}}^{-\text{i}\omega T_{cr}}}{{\left(\text{i}\omega +\mu \right)}^2}\left(K_{11}{A}_1+K_{21}{A}_2\right)\mathrm{.}$ (29)

The algebraic Equations (28)-(29) will have solutions if $\exists c\in ℂ$ such that

$\det \left(\left[\begin{array}{cc}c{K}_{11}-1& c{K}_{21}\\ c{K}_{11}& c{K}_{21}-1\end{array}\right]\right)=\det \left(cK-I\right)=0$ (30)

where

$c=\frac{{\text{e}}^{-i\omega T_{cr}}}{{\left(i\omega +\mu \right)}^2}\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>\; ,\; <mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>}K=\left[\begin{array}{cc}{K}_{11}& K_{21}\\ K_{11}& K_{21}\end{array}\right]\mathrm{.}$ (31)

Equation (30) yields $c\left(K_{11}+K_{21}\right)=1$ which implies Im(c) = 0, that is

$0=\frac{\left({\omega }^2-{\mu }^2\right)\sin \left(\omega T_{cr}\right)-2\omega \mu \cos \left(\omega T_{cr}\right)}{{\left({\mu }^2+{\omega }^2\right)}^2}$ (32)

$\iff T_{cr}=\frac{1}{\omega }\arctan \left(\frac{2\omega \mu }{{\omega }^2-{\mu }^2}\right)$ (33)

Also, $\left(K_{11}+K_{21}\right)\mathrm{Re}\left(c\right)=1$ yields

(34)

$\iff \omega =\sqrt{-{\mu }^2-\left(K_{11}+K_{21}\right)}$ (35)

where we have used the identities

$\sin \left(\omega T_{cr}\right)=\sin \left(\arctan \left(\frac{2\omega \mu }{{\omega }^2-{\mu }^2}\right)\right)=\frac{2\omega \mu }{{\omega }^2+{\mu }^2}$ (36)

$\cos \left(\omega T_{cr}\right)=\cos \left(\arctan \left(\frac{2\omega \mu }{{\omega }^2-{\mu }^2}\right)\right)=\frac{{\omega }^2-{\mu }^2}{{\omega }^2+{\mu }^2}\mathrm{.}$ (37)

The stability analysis presented above shows that the stable equilibrium point $\left({\xi }_1^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}{\xi }_2^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}{\eta }_1^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}{\eta }_2^{\mathrm{<mo>\; *\; </mo>}}\right)$ of the system (10)-(13) loses its stability when $T=T_{cr}$ giving rise to a pair of pure imaginary eigenvalues $\pm \omega \text{i}$ corresponding to the solutions

${\xi }_i\left(t\right)=A_i\cos \left(\omega t+{\varphi }_i\right)$ (38)

${\eta }_i\left(t\right)=B_i\cos \omega t$ (39)

where $A_i$ and $B_i$ are the amplitudes of the ${\eta }_i\left(t\right)$ and ${\xi }_i\left(t\right)$ oscillations, and where ${\varphi }_i$ is a phase angle. Note that without loss of generality we may set the phase ${\varphi }_i=0$ and thus for values of delay T close to $T_{cr}$ we will have $T=T_{cr}+\Delta$ where the nonlinear system (3)-(6) is expected to exhibit a periodic solution for small $\Delta$ . The nonlinear analysis for the two coupled mRNA-protein system follows the same computational steps as the N coupled mRNA-protein system. Thus to avoid redundancy we will postpone its presentation until Section 5.

4. Linear Analysis of N Coupled mRNA-Protein Systems

We now extend our previous linear results to a system of N coupled mRNA-protein systems with feedback and delay. The present analysis follows the steps as the one presented in Section 3, hence, and to avoid repetition, we will present only the main results. The system is depicted in Figure 4 and modeled by the following equations

${\stackrel{\dot{}}{m}}_i=-\mu m_i+{\displaystyle \underset{j=1}{\overset{N}{\sum }}}\frac{1}{1+{\left(\frac{p_{jd}}{p_{j0}}\right)}^n}$ (40)

${\stackrel{\dot{}}{p}}_i=m_i-\mu p_i$ (41)

where $i=1,2,\cdots ,N$ and $p_{jd}=p_j\left(t-T\right)$ . Setting ${\stackrel{\dot{}}{m}}_i={\stackrel{\dot{}}{p}}_i=0$ on (40) and (41) we can show that $\left(\mu p^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}\cdots \mathrm{,}\mu p^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}{p}^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}\cdots \mathrm{,}{p}^{\mathrm{<mo>\; *\; </mo>}}\right)$ is the equilibrium point, where

${\mu }^2{p}^{*}-{\displaystyle \underset{j=1}{\overset{N}{\sum }}}\frac{p_{j0}^n}{p_{j0}^n+p^{*}{}^n}=0$ (42)

Figure 4. Network diagram representing N coupled mRNA-protein systems. Here each mRNA, $m_i$ , is repressed through the interaction with every protein, $p_j$ , via a nonlinear Hill function as given by Equatuon (40). Protein production is affected linearly only by its own mRNA, $m_i$ , and by the associated intrinsic degradation rate $\mu$ as modeled by Equatuon (41). The network exhibits negative feedback, nonlinear interactions, and constant delay, all of which are important components for oscillations.

can be multiplied by the product $\left(p_{10}^n+p^{\mathrm{<mo>\; *\; </mo>}}{}^n\right)\left(p_{20}^n+p^{\mathrm{<mo>\; *\; </mo>}}{}^n\right)\cdots \left(p_{N0}^n+p^{\mathrm{<mo>\; *\; </mo>}}{}^n\right)$ , and thus be made into a polynomial of degree ( $nN+1$ ). The roots of the resulting polynomial can then be approximated using a numerical root finding technique.

Next we define ${\xi }_i=m_i-m^{\mathrm{<mo>\; *\; </mo>}}$ and ${\eta }_i=p_i-p^{\mathrm{<mo>\; *\; </mo>}}$ to be deviations from equilibrium, substitute them into Equations (40)-(41), and expand for small ${\eta }_{jd}$ to obtain

${\stackrel{\dot{}}{\xi }}_i=-\mu {\xi }_i+{\displaystyle \underset{j=1}{\overset{N}{\sum }}}{K}_{j1}{\eta }_{jd}+{\displaystyle \underset{j=1}{\overset{N}{\sum }}}{K}_{j2}{\eta }_{jd}^2+{\displaystyle \underset{j=1}{\overset{N}{\sum }}}{K}_{j3}{\eta }_{jd}^3+\cdots$ (43)

${\stackrel{\dot{}}{\eta }}_i={\xi }_i-\mu {\eta }_i$ (44)

where the Taylor coefficients, $K_{ji}$ , are given as follows

$K_{j1}=-\frac{n{\beta }_j}{{\left(1+{\beta }_j\right)}^2{p}^{*}}\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>},\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>}\text{where}{\beta }_j={\left(\frac{p^{*}}{p_{j0}}\right)}^n$ (45)

$K_{j2}=\frac{n{\beta }_j\left({\beta }_{j}n-n+{\beta }_j+1\right)}{2{\left(1+{\beta }_j\right)}^3{p}^{*2}}$ (46)

$K_{j3}=-\frac{n{\beta }_j\left({\beta }_j^2{n}^2-4{\beta }_j{n}^2+n^2+3{\beta }_j^{2}n-3n+2{\beta }_j^2+4{\beta }_j+2\right)}{6{\left(1+{\beta }_j\right)}^4{p}^{*3}}$ (47)

To show the steady state is stable when $T=0$ (no delay), we consider the 2N-dimensional linearized system coming from Equations (43)-(44)

${\stackrel{\dot{}}{\xi }}_i=-\mu {\xi }_i+{\displaystyle \underset{j=1}{\overset{N}{\sum }}}{K}_{j1}{\eta }_{jd}$ (48)

${\stackrel{\dot{}}{\eta }}_i={\xi }_i-\mu {\eta }_i$ (49)

with its associated Jacobian matrix

$J={\left[\begin{array}{cc}M& K\\ I& M\end{array}\right]}_{2N\times 2N}$ (50)

where I is the $N\times N$ identity matrix, $M=-\mu I$ , and

$K={\left[\begin{array}{ccccc}{K}_{1,1}& K_{2,1}& \cdots & K_{N-1,1}& K_{N,1}\\ K_{1,1}& K_{2,1}& \cdots & K_{N-1,1}& K_{N,1}\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ K_{1,1}& K_{2,1}& \cdots & K_{N-1,1}& K_{N,1}\\ K_{1,1}& K_{2,1}& \cdots & K_{N-1,1}& K_{N,1}\end{array}\right]}_{N\times N}$ (51)

To find the eigenvalues, $\lambda$ , of the block Jacobian matrix, J, we compute

$\det \left(\left[\begin{array}{cc}M-\lambda I& K\\ I& M-\lambda I\end{array}\right]\right)=\det \left({\left(\mu +\lambda \right)}^{2}I-K\right)=0$ (52)

which gives the following eigenvalues

$\left\{-\mu ,-\mu \pm \sqrt{{\displaystyle \underset{j=1}{\overset{N}{\sum }}}{K}_{j1}}\right\}$ (53)

where $\mu >0$ (multiplicity $2N-2$ ) and since $K_{j1}<0$ $\forall j$ then the square root term in Equation (53) will be imaginary and thus $\mathrm{Re}\left(\lambda \right)<0$ for all $\lambda$ . This shows that the equilibrium solution is stable for $T=0$ .

To find the critical delay, $T=T_{cr}$ , we assume solutions of the form ${\eta }_i=A_i{\text{e}}^{\lambda t}$ and ${\xi }_i=B_i{\text{e}}^{\lambda t}$ , substitute them into (48)-(49), and set $T=T_{cr}$ and $\lambda =\text{i}\omega$ to obtain the linear system

$A_i=c{\displaystyle \underset{j=1}{\overset{N}{\sum }}}{K}_{j1}{A}_j$ (54)

where $c=\frac{{\text{e}}^{-\text{i}\omega T_{cr}}}{{\left(\text{i}\omega +\mu \right)}^2}\in ℂ$ . System (54) will have nontrivial solutions when $\det \left(cK-I\right)=0$ which gives $c{\displaystyle {\sum }_{j=1}^N}{K}_{j1}=N$ and thus

$T_{cr}=\frac{1}{\omega }\arctan \left(\frac{2\omega \mu }{{\omega }^2-{\mu }^2}\right)$ (55)

$\omega =\sqrt{-{\mu }^2-{\displaystyle \underset{j=1}{\overset{N}{\sum }}}{K}_{j1}}$ (56)

where we have used the identities (36)-(37) and where the nonlinear system (40)-(41) is expected to exhibit periodic solutions for $T=T_{cr}+\Delta$ when $\Delta \ll 1$ .

5. Nonlinear Analysis of the N Coupled System

We use the Poincare-Lindstedt’s perturbation method to find closed form approximate expressions for the amplitude of the limit cycle born at the Hopf bifurcation. This will be accomplished by considering the full nonlinear system (43)-(44) and perturbing off of the critical delay, $T=T_{cr}$ . We start by combining Equations (43)-(44) into a system of second order DDEs

${\ddot{\eta }}_i+2\mu {\stackrel{\dot{}}{\eta }}_i+{\mu }^2{\eta }_i\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}=\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}{\displaystyle \underset{j=1}{\overset{N}{\sum }}}{K}_{j1}{\eta }_{jd}+{\displaystyle \underset{j=1}{\overset{N}{\sum }}}{K}_{j2}{\eta }_{jd}^2+{\displaystyle \underset{j=1}{\overset{N}{\sum }}}{K}_{j3}{\eta }_{jd}^3+\cdots$ (57)

where $i=1,2,\cdots ,N$ , and $K_{j1}$ , $K_{j2}$ , and $K_{j3}$ are the Taylor coefficients given by Equations (45)-(47), respectively. Next we introduce a small parameter $\epsilon$ via the following scaling

${\eta }_i\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}=\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}\epsilon u_i,$ (58)

stretch time by defining a new independent variable

$\tau \mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}=\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}\Omega t,$ (59)

and expand $\Omega$ in a power series in $\epsilon$ as follows

$\Omega \mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}=\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}\omega +{\epsilon }^2{k}_2+\cdots$ (60)

where we omit the $O\left(\epsilon \right)$ term since it turns out to be zero. We substitute Equations (58) and (59) into (57) to obtain

${\Omega }^2\frac{{\text{d}}^2{u}_i}{\text{d}{\tau }^2}+2\mu \Omega \frac{\text{d}{u}_i}{\text{d}\tau }+{\mu }^2{u}_i-{\displaystyle \underset{j=1}{\overset{N}{\sum }}}{K}_{j1}{u}_{jd}\mathrm{<mi>\; </mi>}=\mathrm{<mi>\; </mi>}\epsilon {\displaystyle \underset{j=1}{\overset{N}{\sum }}}{K}_{j2}{u}_{jd}^2+{\epsilon }^2{\displaystyle \underset{j=1}{\overset{N}{\sum }}}{K}_{j3}{u}_{jd}^3+\cdots$ (61)

which will be used after perturbing the delay about $T_{cr}$ and Taylor expanding $u_i$ and $u_{jd}$ . We accomplish the latter by scaling the detuning $\Delta$ as follows

$T\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}=\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}{T}_{cr}+\Delta \mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}=\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}{T}_{cr}+{\epsilon }^2\delta$ (62)

and expanding $u_i\left(\tau \right)$ in a power series in $\epsilon$

$u_i\left(\tau \right)\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}=\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}{u}_{i0}\left(\tau \right)+\epsilon u_{i1}\left(\tau \right)+{\epsilon }^2{u}_{i2}\left(\tau \right)+\cdots .$ (63)

Substituting Equations (60) and (62) into $u_{jd}=u_j\left(\tau -\Omega T\right)$ and Taylor expanding about $\epsilon =0$ we obtain

$\begin{array}{c}{u}_{jd}=u_j\left(\tau -\Omega T\right)=u_j\left(\tau -\omega T_{cr}-{\epsilon }^2\left(k_2{T}_{cr}+\omega \delta \right)+\cdots \right)\\ =u_j\left(\tau -\omega T_{cr}\right)-{\epsilon }^2\left(k_2{T}_{cr}+\omega \delta \right){u^{\prime }}_j\left(\tau -\omega T_{cr}\right)+\cdots .\end{array}$ (64)

Substituting Equations (60), (63) and (64) into (61), and collecting like powers of $\epsilon$ we find

${\omega }^2\frac{{\text{d}}^2{u}_{i0}}{\text{d}{\tau }^2}+2\mu \omega \frac{\text{d}{u}_{i0}}{\text{d}\tau }+{\mu }^2{u}_{i0}-{\displaystyle \underset{j=1}{\overset{N}{\sum }}}{K}_{j1}{u}_{j0}\left(\tau -\omega T_{cr}\right)=0$ (65)

${\omega }^2\frac{{\text{d}}^2{u}_{i1}}{\text{d}{\tau }^2}+2\mu \omega \frac{\text{d}{u}_{i1}}{\text{d}\tau }+{\mu }^2{u}_{i1}-{\displaystyle \underset{j=1}{\overset{N}{\sum }}}{K}_{j1}{u}_{j1}\left(\tau -\omega T_{cr}\right)={\displaystyle \underset{j=1}{\overset{N}{\sum }}}{K}_{j2}{u}_{j0}^2\left(\tau -\omega T_{cr}\right)$ (66)

${\omega }^2\frac{{\text{d}}^2{u}_{i2}}{\text{d}{\tau }^2}+2\mu \omega \frac{\text{d}{u}_{i2}}{\text{d}\tau }+{\mu }^2{u}_{i2}-{\displaystyle \underset{j=1}{\overset{N}{\sum }}}{K}_{j1}{u}_{j2}\left(\tau -\omega T_{cr}\right)=\cdots$ (67)

where $\cdots$ stands for terms in $u_{i0}$ and $u_{i1}$ , omitted here for brevity.

The next step is to solve Equations (65)-(67). We start with Equation (65) by setting the solutions, $u_{i0}$ , as

$u_{i0}\left(\tau \right)=\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}\hat{A}\cos \tau$ (68)

where by Equation (58) we know ${\eta }_{i0}=\epsilon u_{i0}=\epsilon \hat{A}\cos \tau =A\cos \tau$ . Next we substitute (68) into (66) and obtain the following expression for $u_{i1}$

$u_{i1}\left(\tau \right)=m_{i1}\sin 2\tau +m_{i2}\cos 2\tau +m_{i3}$ (69)

where $m_{i1}$ is given by the equation:

$m_{i1}=-\frac{2{\hat{A}}^2{\hat{K}}_2\mu {\omega }^3\left(2{\mu }^2+3{\hat{K}}_1\right)}{{\hat{K}}_1\left(16{\mu }^6+39{\hat{K}}_1{\mu }^4+18{\hat{K}}_1^2{\mu }^2-9{\hat{K}}_1^3\right)}$ (70)

where

${\hat{K}}_1=\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}{\displaystyle \underset{j=1}{\overset{N}{\sum }}}{K}_{j1},\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>}{\hat{K}}_2={\displaystyle \underset{j=1}{\overset{N}{\sum }}}{K}_{j2}\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>}\text{and}\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>}{\hat{K}}_3={\displaystyle \underset{j=1}{\overset{N}{\sum }}}{K}_{j3}$ (71)

and where we omit the expressions for $m_{i2}$ and $m_{i3}$ for brevity.

Next we substitute Equations (68) and (69) into (67), and after trigonometric simplifications have been performed, we equate to zero the coefficients of the resonant terms $\sin \tau$ and $\cos \tau$ . This yields the amplitude, A, of the limit cycle that was born in the Hopf bifurcation

$A^2=\frac{P}{Q}\Delta$ (72)

where

$P=8{\hat{K}}_1^2{\omega }^2\left({\mu }^2-{\hat{K}}_1\right)\left(16{\mu }^6+39{\hat{K}}_1{\mu }^4+18{\hat{K}}_1^2{\mu }^2-9{\hat{K}}_1^3\right)$ (73)

$Q=Q_0{T}_{cr}+Q_1$ (74)

and

$\begin{array}{c}{Q}_0=48{\hat{K}}_3{\hat{K}}_1^2{\mu }^8-16{\hat{K}}_2^2{\hat{K}}_1{\mu }^8+69{\hat{K}}_3{\hat{K}}_1^3{\mu }^6+32{\hat{K}}_2^2{\hat{K}}_1^2{\mu }^6\\ -63{\hat{K}}_3{\hat{K}}_1^4{\mu }^4+162{\hat{K}}_2^2{\hat{K}}_1^3{\mu }^4-81{\hat{K}}_3{\hat{K}}_1^5{\mu }^2+108{\hat{K}}_2^2{\hat{K}}_1^4{\mu }^2\\ +27{\hat{K}}_3{\hat{K}}_1^6-30{\hat{K}}_2^2{\hat{K}}_1^5\end{array}$ (75)

$\begin{array}{c}{Q}_1=-96{\hat{K}}_3{\hat{K}}_1{\mu }^9+64{\hat{K}}_2^2{\mu }^9-138{\hat{K}}_3{\hat{K}}_1^2{\mu }^7+16{\hat{K}}_2^2{\hat{K}}_1{\mu }^7\\ +126{\hat{K}}_3{\hat{K}}_1^3{\mu }^5-308{\hat{K}}_2^2{\hat{K}}_1^2{\mu }^5+162{\hat{K}}_3{\hat{K}}_1^4{\mu }^3-296{\hat{K}}_2^2{\hat{K}}_1^3{\mu }^3\\ -54{\hat{K}}_3{\hat{K}}_1^5\mu +12{\hat{K}}_2^2{\hat{K}}_1^4\mu \end{array}$ (76)

and where the ${\hat{K}}_i$ ’s are given by Equation (71) and Equations (45)-(47). Equation (72) gives the amplitude of the limit cycle born at the Hopf bifurcation in terms of the original system parameters. The numerical values are calculated via a computer routine and the outcome for different N will be presented in Section 6.

6. Numerical Results

In this section we use our closed form expressions to investigate the nonlinear behavior of Equations (40)-(41) close to the Hopf bifurcation. Setting $T=T_{cr}+\Delta$ , $\mu =0.2$ , $p_{j0}=2$ , and $n=3$ , we compute the amplitude of the limit cycle born at the Hopf by using Equation (72). Our results for $N=2$ , summarized in Figure 5, show that the Hopf occurs at $T_{cr}=0.3087$ and the amplitude of the limit cycle grows as $\Delta$ becomes larger. Several points along the amplitude curve were tested using MATLAB’s built-in function dde23.m on the original DDE system (40)-(41). Figure 5 shows a comparison between our perturbation curve and eight points computed with MATLAB, all of which were in agreement. In addition, we also present one dde23.m numerical simulation, point a5, which shows that the amplitude is approximately 4.350 when $\Delta =0.05$ .

Figure 5. Amplitude VS Detuning graph. $T_{cr}=0.3087$ was calculated using Equatuon (55) and the amplitudes calculated using various detuning (Delta) values as described in the table. Here we present one explicit numerical simulation result for $T=0.3087+0.050$ , labeled as point a5, which was obtained using MATLAB’s built-in function dde23.m. The rest of the amplitude values were confirmed using MATLAB on the full nonlinear system (40)-(41).

Figure 6. Amplitude VS Detuning plots for N = 2, 7, 15, and 30. Other parameter values were set as $n=3$ and $p_{j0}=2$ for $j=1,2,\cdots ,N$ . Table shows numerical values for the different amplitudes obtained for various N.

Figure 6 shows the same analysis described above for $N=2,7,15$ and 30. Different values of $T_{cr}$ were found for each N and the detuning was set as $0\le \Delta \le 0.230$ for comparison purposes. These results were all confirmed with MATLAB and they show the accuracy of our closed form expressions in predicting the critical delay, stability, and amplitude of the oscillation for large values of N. In addition, they also show the influence and significance of the original model parameters on the system’s dynamics, where (regardless of N) our model will always exhibit a transition between equilibrium and oscillation due to a Hopf bifurcation. We point out, however, that our perturbation results did not match MATLAB’s numerical findings for $\Delta >0.230$ . This is attributed to the nature of our perturbation technique, where the results are guaranteed for small $\epsilon$ as given by Equation (62). Thus, the limits of this approach rely on $\Delta \ll 1$ , that is, they are limited to a small neighborhood about $T=T_{cr}$ , which is commonly the case with any kind of perturbation technique.

7. Conclusions

In this paper we investigated the periodic solutions of a mRNA-protein nonlinear model with negative feedback and delay. Nonlinear models exhibiting these features are usually good candidates for periodic behavior. In this work we show that, regardless of the size of the network, having these features yields a dynamical system that always transitions from a stable steady state to a limit cycle oscillation via a Hopf bifurcation. The standard approach to study Hopf bifurcations for DDEs is to use the more conventional center manifold approximation [17] [18] . However, for a network of this size, this would be a computationally intractable endeavor and thus our approach presents a new way on how these perturbation techniques are a useful tool to better understand the dynamics of large networks with nonlinear interactions and delays.

Our closed form approximate expressions for the amplitude of the limit cycle provide a useful way to understand the different roles that the system’s parameters play in the dynamics of the periodic motion. We point out, however, that our linear and nonlinear computational analyses are possible due to the symmetric nature of our network: where we have assumed that all the systems share the same degradation rate $\mu$ , every mRNA is equally repressed by every protein, and biological location within the cell is not taken into account. Regardless of these simplifications, this study shows the importance of the nonlinearities arising from the Hill term in Equation (40) and the delay, both of which give rise to the periodic dynamics of the system. Future research efforts should be directed towards relaxing these symmetric conditions. For example, including a “weighting” function on the Hill term of Equation (40) would take into account the net effect that a protein has on each mRNA. The latter would be more significant, from a biological viewpoint, because not every protein represses equally each mRNA. Another direction would be to assume different degradation rates ${\mu }_i$ ’s for each protein and mRNA. Finally, considering different synthesis rates, ${\alpha }_m$ and ${\alpha }_p$ , would be another interesting direction that could allow us to classify the significance of each of these biological parameters with regards to the system’s periodic behavior. The analysis of the system in these new directions proves to be computationally cumbersome from a perturbation analysis point of view. However, new findings in the fields of DDEs and perturbation theory will prove that these research directions will provide more insight into the rich dynamics exhibited by these networks.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Alberts, B., Johnson, A., Lewis, J., Morgan, D., Raff, M., Roberts, K. and Walter, P. (2015) Molecular Biology of the Cell. Garland Science, New York.
[2]	Ay, A. and Arnosti, D.N. (2011) Mathematical Modeling of Gene Expression: A Guide for the Perplexed Biologist. Critical Reviews in Biochemistry and Molecular Biology, 46, 137-151. https://doi.org/10.3109/10409238.2011.556597
[3]	Elowitz, M.B. and Leibler, S. (2000) A Synthetic Oscillatory Network of Transcriptional Regulators. Nature, 403, 335-338. https://doi.org/10.1038/35002125
[4]	Gardner, T.S., Cantor, C.R. and Collins, J.J. (2000) Construction of a Genetic Toggle Switch in Escherichia coli. Nature, 403, 339-342. https://doi.org/10.1038/35002131
[5]	Ciliberti, A., Novak, B. and Tyson, J.J. (2005) Steady States and Oscillations in the p53/Mdm2 Network. Cell Cycle, 4, 488-493. https://doi.org/10.4161/cc.4.3.1548
[6]	Muller, S., Hofbauer, J., Endler, L., Flamm, C., Widder, S. and Schuster, P. (2006) A Generalized Model of the Repressilator. Journal of Mathematical Biology, 53, 905-937. https://doi.org/10.1007/s00285-006-0035-9
[7]	Hasty, J., McMillen, D., Isaacs, F. and Collins, J.J. (2001) Computational Studies of Gene Regulatory Networks: In Numero Molecular Biology. Nature, 2, 268-279. https://doi.org/10.1038/35066056
[8]	Jong, H. (2002) Modeling and Simulation of Genetic Regulatory Systems: A Literature Review. Journal of Computational Biology, 9, 67-103. https://doi.org/10.1089/10665270252833208
[9]	Schlitt, T. and Brazma, A. (2007) Current Approaches to Gene Regulatory Network Modelling. BMC Bioinformatics, 8, S9. https://doi.org/10.1186/1471-2105-8-S6-S9
[10]	Conrad, E.D. and Tyson, J.J. (2006) Modeling Molecular Interaction Networks with Nonlinear Ordinary Differential Equations. MIT Press, Cambridge, 97-123. https://doi.org/10.7551/mitpress/9780262195485.003.0006
[11]	Mochizuki, A. (2007) Structure of Regulatory Networks and Diversity of Gene Expression Patterns. Journal of Theoretical Biology, 250, 307-321. https://doi.org/10.1016/j.jtbi.2007.09.019
[12]	Bratsun, D., Volfson, D., Tsimring, L.S. and Hasty, J. (2005) Delay-Induced Stochastic Oscillations in Gene Regulation. PNAS, 102, 14593-14598. https://doi.org/10.1073/pnas.0503858102
[13]	Edwards, R., van den Driessche, P. and Wang, L. (2007) Periodicity in Piecewise-Linear Switching Networks with Delay. Journal of Mathematical Biology, 55, 271-298. https://doi.org/10.1007/s00285-007-0084-8
[14]	Verdugo, A. and Rand, R. (2008) Hopf Bifurcation in a DDE Model of Gene Expression. Communications in Nonlinear Science and Numerical Simulation, 13, 235-242. https://doi.org/10.1016/j.cnsns.2006.05.001
[15]	Monk, N.A.M. (2003) Oscillatory Expression of Hes1, p53, and NF-κB Driven by Transcriptional Time Delays. Current Biology, 13, 1409-1413. https://doi.org/10.1016/S0960-9822(03)00494-9
[16]	Zeiser, S., Muller, J. and Liebscher, V. (2007) Modeling the Hes1 Oscillator. Journal of Computational Biology, 14, 984-1000. https://doi.org/10.1089/cmb.2007.0029
[17]	Verdugo, A. and Rand, R. (2008) Center Manifold Analysis of a DDE Model of Gene Expression. Communications in Nonlinear Science and Numerical Simulation, 13, 1112-1120. https://doi.org/10.1016/j.cnsns.2006.09.011
[18]	Kalmar-Nagy, T., Stepan, G. and Moon, F. (2001) Subcritical Hopf Bifurcation in the Delay Equation Model for Machine Tool Vibrations Nonlinear Dynamics, 26, 121-142. https://doi.org/10.1023/A:1012990608060