A Matrix Inequality for the Inversions of the Restrictions of a Positive Definite Hermitian Matrix ()
1. Introduction and Results
By exploiting the general structure of reproducing kernel Hilbert spaces, it is possible to prove very interesting norm inequalities (see, e.g., [1,2]). A typical result is as follows.
Let  be an N-ply connected regular domain whose boundary consists of disjoint analytic Jordan curves. Let
be an N-ply connected regular domain whose boundary consists of disjoint analytic Jordan curves. Let 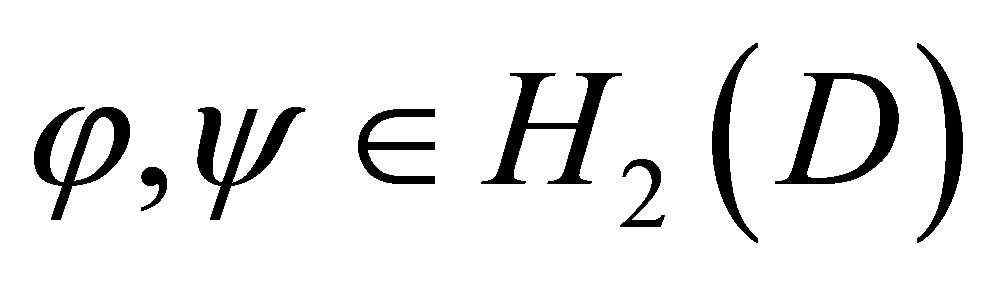 be analytic Hardy functions with index two. Then the following generalised isoperimetric inequality holds,
be analytic Hardy functions with index two. Then the following generalised isoperimetric inequality holds,

Moreover, we can completely describe the cases for which we have the equality instead of the inequality here above. Without the theory of reproducing kernels, such a simple and beautiful inequality could not be derived (see [2,3] for the details).
In this paper we introduce a new inequality. Let  be a positive definite Hermitian matrix. Let
be a positive definite Hermitian matrix. Let  and let
and let  be the restriction of
be the restriction of  to an
to an 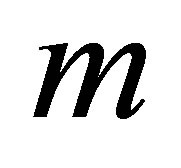 dimensional subspace of
dimensional subspace of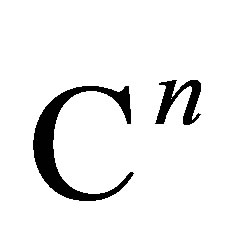 . Without loss of generality, assume that
. Without loss of generality, assume that  is the
is the  leading principal minor of
leading principal minor of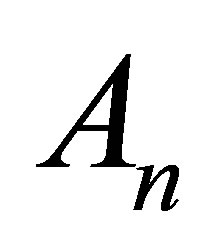 . Let
. Let  and
and 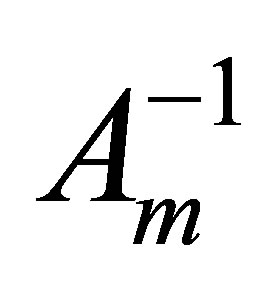 denote the inverse of
denote the inverse of  and of
and of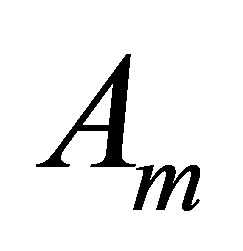 , respectively. Then we have the following results.
, respectively. Then we have the following results.
Theorem 1.1 If  and
and 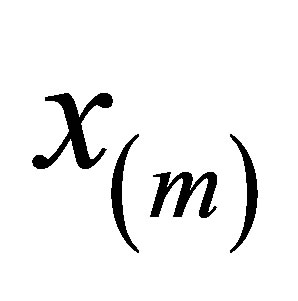 is the vector of
is the vector of 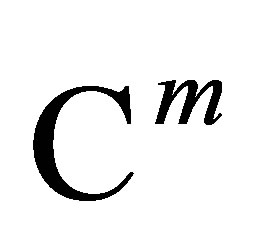 defined by
defined by , then
, then
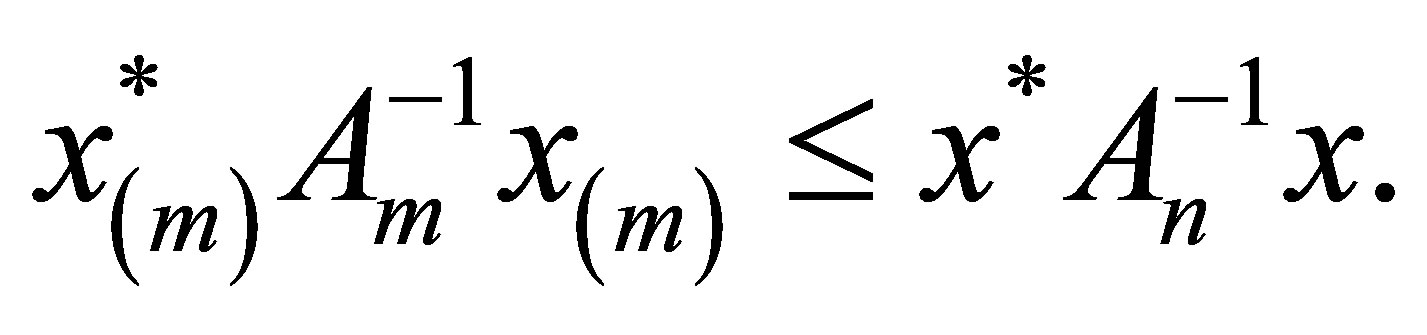 (1)
(1)
Here  denotes conjugate transpose. As an immediate consequence, one also obtains the following corollary.
denotes conjugate transpose. As an immediate consequence, one also obtains the following corollary.
Corollary 1.2 If  is the restriction of the matrix
is the restriction of the matrix  to
to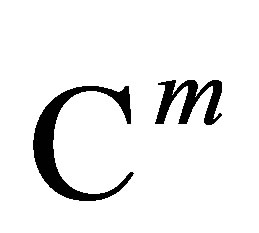 , then
, then
 (2)
(2)
Here  denotes the positive definite order, i.e., if
denotes the positive definite order, i.e., if 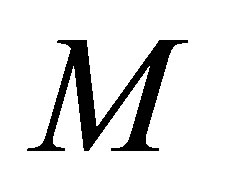 and
and  are square matrices, we say that
are square matrices, we say that  if
if  is a positive semi-definite matrix.
is a positive semi-definite matrix.
We observe that for , such results can be checked directly. However, for
, such results can be checked directly. However, for , the result of Theorem 1.1 is not intuitive and appears mysterious, at least at first glance.
, the result of Theorem 1.1 is not intuitive and appears mysterious, at least at first glance.
2. Proof of the Results
The proof of Theorem 1.1 is based on the theory of reproducing kernels. Therefore, we begin by introducing some notions and results which are used in the sequel.
2.1. Reproducing Kernels
Let  be an arbitrary abstract (non-void) set. Let
be an arbitrary abstract (non-void) set. Let  denote the set of all complex-valued functions on
denote the set of all complex-valued functions on . A reproducing kernel Hilbert spaces (RKHS for short) on the set
. A reproducing kernel Hilbert spaces (RKHS for short) on the set  is a Hilbert space
is a Hilbert space  endowed with a function
endowed with a function , which is called the reproducing kernel and which satisfies the reproducing property. Namely we have
, which is called the reproducing kernel and which satisfies the reproducing property. Namely we have
 (3)
(3)
and
 (4)
(4)
for all  and for all
and for all . We denote by
. We denote by  (or
(or ) the reproducing kernel Hilbert space
) the reproducing kernel Hilbert space  whose corresponding reproducing function is
whose corresponding reproducing function is .
.
A complex-valued function  is called a positive definite quadratic form function on the set
is called a positive definite quadratic form function on the set , or shortly, positive definite function, if, for an arbitrary function
, or shortly, positive definite function, if, for an arbitrary function  and for any finite subset
and for any finite subset  of
of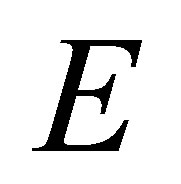 , one has
, one has
 (5)
(5)
By a fundamental theorem, we know that, for any positive definite quadratic form function  on
on , there exists a unique reproducing kernel Hilbert space on
, there exists a unique reproducing kernel Hilbert space on  with reproducing kernel
with reproducing kernel . So, in a sense, the correspondence between the reproducing kernel
. So, in a sense, the correspondence between the reproducing kernel  and the reproducing kernel Hilbert space
and the reproducing kernel Hilbert space  is one to one.
is one to one.
A simple example of positive definite quadratic form function is a positive definite Hermitian matrix.
Example 2.1 Let  be a set consisting of
be a set consisting of  distinct points. Let
distinct points. Let  be a strictly positive
be a strictly positive  Hermitian matrix. Let
Hermitian matrix. Let
 denote the inverse of
denote the inverse of . Then the space
. Then the space
 of the complex valued functions on
of the complex valued functions on , endowed with the inner product
, endowed with the inner product

is a reproducing kernel Hilbert (complex Euclidean) space with reproducing kernel  defined by
defined by 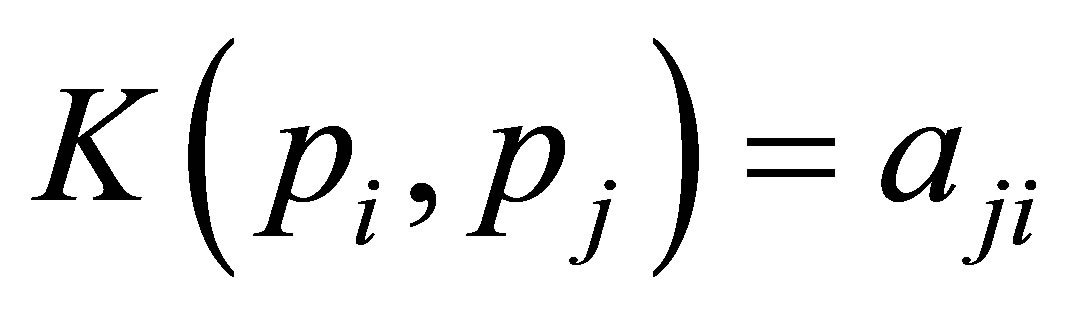 for all
for all .
.
Indeed, the validity of (3) follows by a straightforward calculation. To prove (4) we observe that

for all  (note that
(note that ). Thus
). Thus  coincides with the reproducing kernel Hilbert space
coincides with the reproducing kernel Hilbert space . In particular the norm induced by the product
. In particular the norm induced by the product 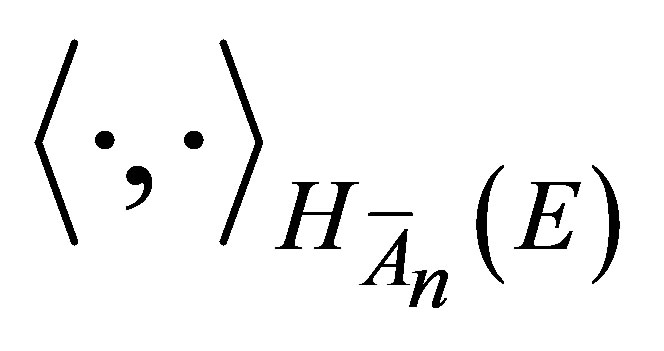 coincides with the norm of
coincides with the norm of .
.
We can thus combine the two theories of postitive definite Hermitian matrices and of reproducing kernels (see [4-12]).
2.2. Restriction of a Reproducing Kernel
The validity of Theorem 1.1 follows by the properties of the restriction of a reproducing kernel in a general setting. Let  be a non-empty set and let
be a non-empty set and let  be a non-empty subset of
be a non-empty subset of . Let
. Let  be a positive definite quadratic form function. Then the restriction
be a positive definite quadratic form function. Then the restriction  of
of  to
to  is a positive definite quadratic form function on
is a positive definite quadratic form function on  and the relation between
and the relation between 
and  is given by the following statement.
is given by the following statement.
Proposition 2.1 (Restriction of RKHS) Let  be a non-empty set and let
be a non-empty set and let  be a non-empty subset of
be a non-empty subset of . Let
. Let  be a positive definite quadratic form function. Then the Hilbert space defined by the positive definite quadratic form function
be a positive definite quadratic form function. Then the Hilbert space defined by the positive definite quadratic form function  is given by
is given by
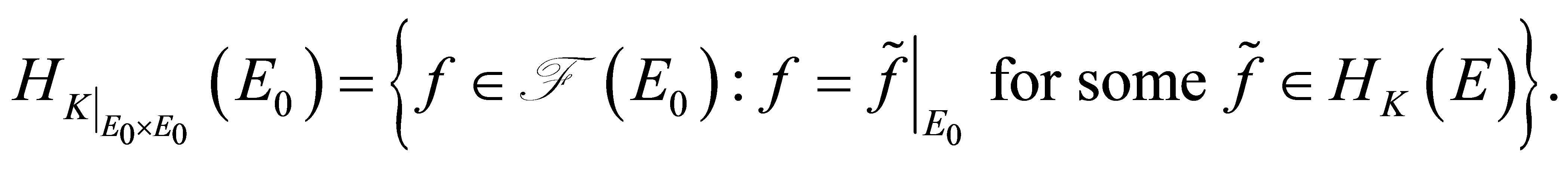 (6)
(6)
Furthermore, the norm of 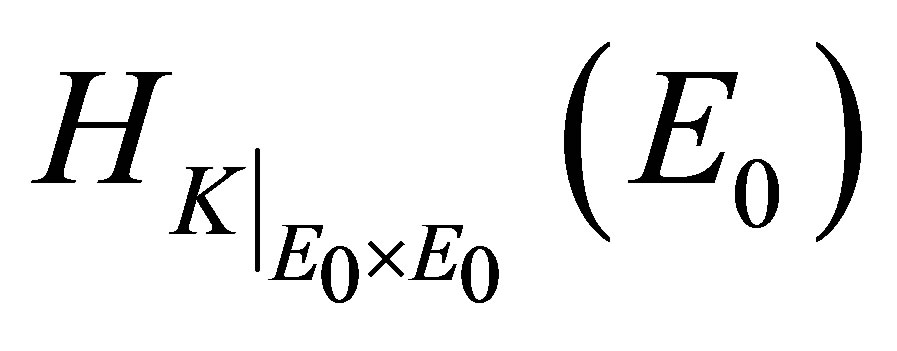 is expressed in terms of the norm of
is expressed in terms of the norm of  by the following equality,
by the following equality,
 (7)
(7)
which holds for all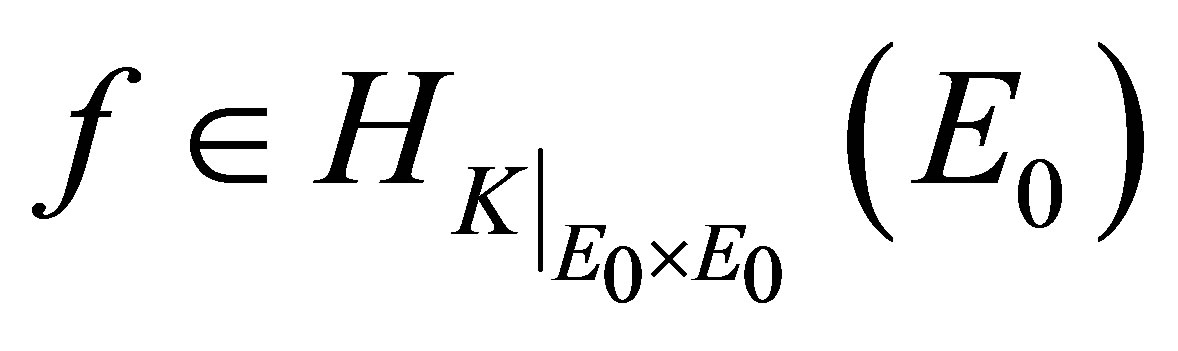 .
.
See [1] for the details.
2.3. Proof of Theorem 1.1
Let 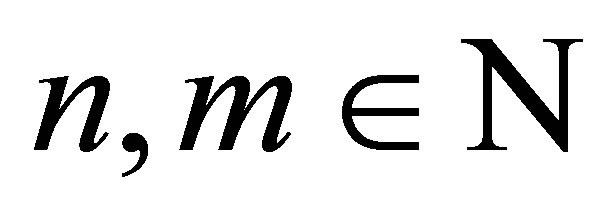 with
with . Let
. Let  and
and . Let
. Let  be the positive definite quadratic form function on
be the positive definite quadratic form function on  defined by
defined by  for all
for all  Let
Let  and
and . Let
. Let  be the function on
be the function on  defined by
defined by 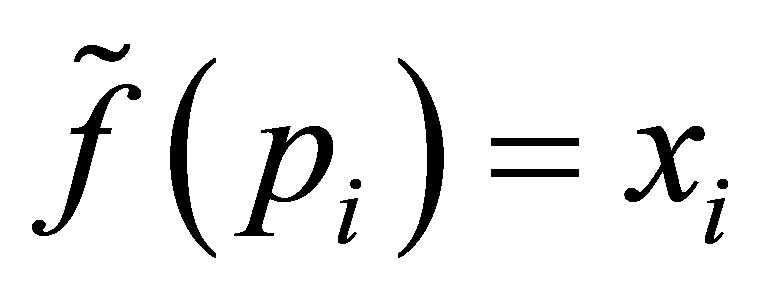 for all
for all . Let
. Let . Then we have
. Then we have
 and
and
 . Thus (7)
. Thus (7)
implies that .
.
3. An Alternative Proof Based on Schur Complement
We provide in this section a direct proof of Theorem 1.1 based on the properties of the Schur complement (cf., e.g., [13]). Let  with
with . Let
. Let  be a positive definite Hermitian
be a positive definite Hermitian 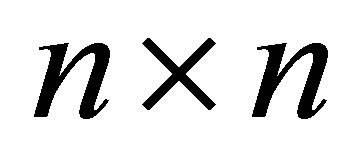 matrix and assume that
matrix and assume that

where 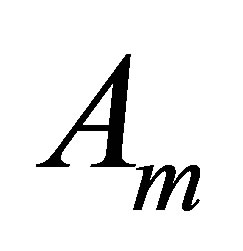 is an
is an  matrix,
matrix,  is an
is an  matrix, and
matrix, and 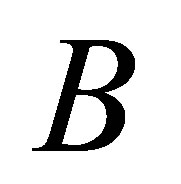 is an
is an  matrix. Observe that
matrix. Observe that 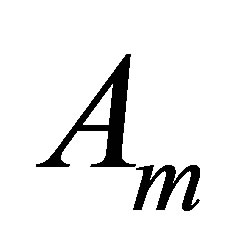 is positive definite and henceforth invertible. Then the inverse
is positive definite and henceforth invertible. Then the inverse 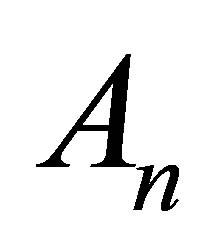 can be written in the form
can be written in the form

where  is the Schur complement with respect to
is the Schur complement with respect to . Since
. Since  we also have
we also have 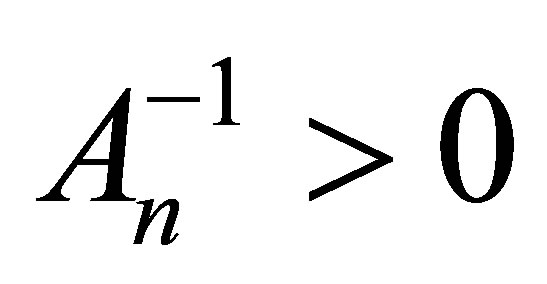 which implies that
which implies that . We now observe that the validity of Theorem 1.1 is equivalent to say that the matrix
. We now observe that the validity of Theorem 1.1 is equivalent to say that the matrix  defined by
defined by
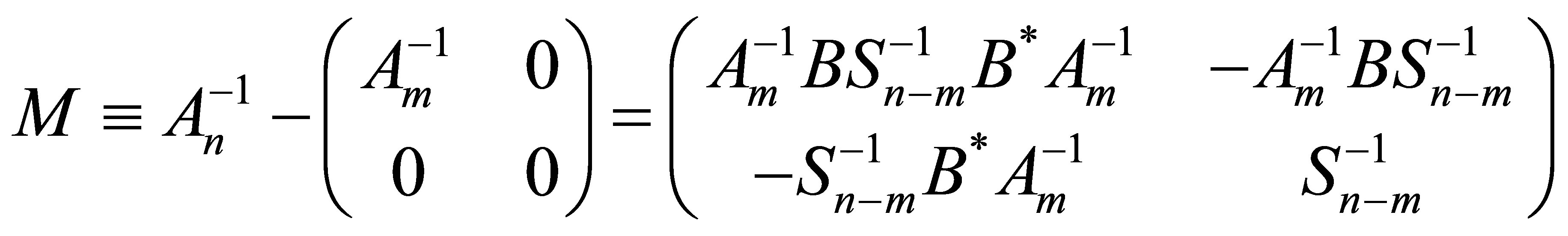
is positive semi-definite. Let 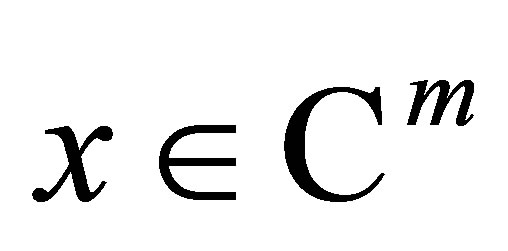 and
and . Then we calculate
. Then we calculate
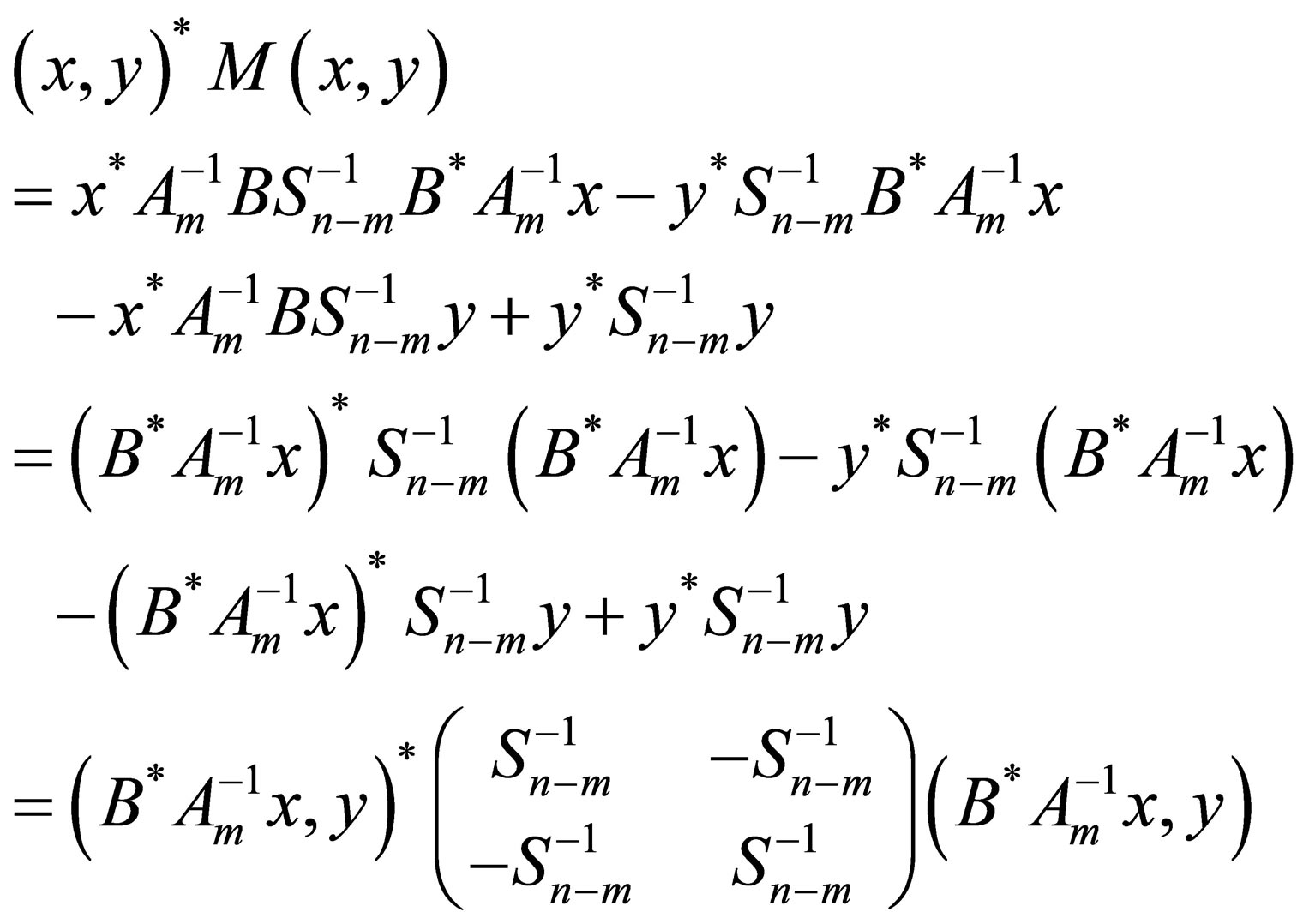
(here we understand that 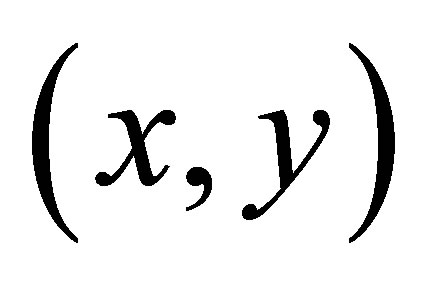 and
and 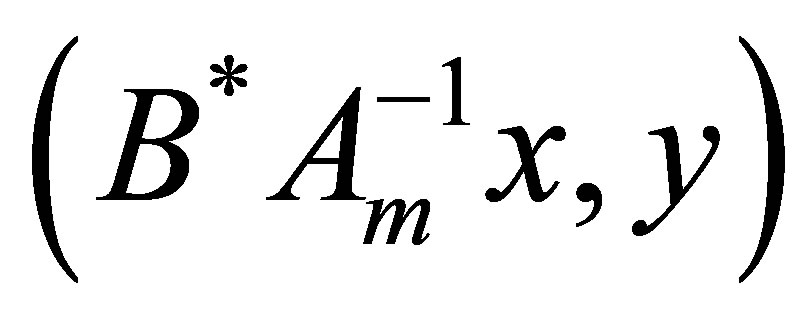 are column vectors). Now we observe that
are column vectors). Now we observe that

where  denotes the Kronecker product of matrices. It is known that the Kronecker product of positive semidefinite matrices is positive semi-definite. Now
denotes the Kronecker product of matrices. It is known that the Kronecker product of positive semidefinite matrices is positive semi-definite. Now

and , hence
, hence

is positive semi-definite and accordingly  . Our proof is completed.
. Our proof is completed.
4. Remark
The results in this paper were given implicitly in the extensive paper [14]. However, such results were not explicitly stated in the corresponding Theorem (Ultimate realization of reproducing kernel Hilbert spaces). For this reason, we wrote this paper where we clearly present our Theorem 1.1. We note that such ideas have arisen to our attention while analysing the structure of the theorem from the viewpoint of the support vector machine for the practical calculation.
5. Acknowledgements
The last author wishes to express his sincere gratitude to Professor Tsuyoshi Ando for providing exciting informations on system theory and the Schur complement. He is supported in part by the Grant-in-Aid for the Scientific Research (C)(2) (No. 24540113).
The research of M. Dalla Riva was supported by FEDER funds through COMPETE—Operational Programme Factors of Competitiveness (“Programa Operacional Factores de Competitividade”) and by Portuguese funds through the Center for Research and Development in Mathematics and Applications (University of Aveiro) and the Portuguese Foundation for Science and Technology (“FCT—Fundação para a Ciência e a Tecnologia”), within project PEst-C/MAT/UI4106/2011 with the Compete number FCOMP-01-0124-FEDER-022690. The research was also supported by the Portuguese Foundation for Science and Technology (“FCT—Fundação para a Ciência e a Tecnologia”) with the research grant SFRH/ BPD/64437/2009 and by “Progetto di Ateneo: Singular perturbation problems for differential operators”—University of Padova.