Constructing Entanglers in 2-Players–N-Strategies Quantum Game

Yshai Avishai^*

Department of Physics and the Ilse Katz Center for Nano-Science, Ben-Gurion University, Beersheba, Israel.

DOI: 10.4236/jqis.2015.51003                

Abstract

In quantum games based on 2-player-N-strategies classical games, each player has a quNit (a normalized vector in an N-dimensional Hilbert space H_N) upon which he applies his strategy (a matrix U∈SU(N)). The players draw their payoffs from a state . Here  and J (both determined by the game’s referee) are respectively an unentangled 2-quNit (pure) state and a unitary operator such that  is partially entangled. The existence of pure strategy Nash equilibrium in the quantum game is intimately related to the degree of entanglement of . Hence, it is practical to design the entangler J= J(β) to be dependent on a single real parameter β that controls the degree of entanglement of , such that its von-Neumann entropy S_N(β) is continuous and obtains any value in . Designing J(β) for N=2 is quite standard. Extension to N>2 is not obvious, and here we suggest an algorithm to achieve it. Such construction provides a special quantum gate that should be a useful tool not only in quantum games but, more generally, as a special gate in manipulating quantum information protocols.

Keywords

Quantum Games, Qubits, Qutrits, quNits, Controlled Entanglement, von Neumann Entropy

1. Introduction

The theory of quantum games is an evolving discipline that, similar to quantum information [1] [2] , explores the implications of quantum mechanics to fields outside physics proper, such as economics, finance, auctions, gambling, etc. [3] - [9] . One way of constructing a quantum game is to start from a standard (classical) game and to “quantize” it by formulating appropriate rules and letting the players employ quantum information tools such as qubits and quantum gates (or strategies in the quantum game nomenclature). This procedure has been applied on classical strategic games that describe an interactive decision-making in which each player chooses his strategy only once, and all choices are taken simultaneously. A simple example is a quantum game based on 2-player-2- strategies classical game usually defined by a game table (for example, the prisoner dilemma). We refer to it briefly as a 2-2 game.

2. Quantum Games: The Role of Entanglement

There is an extensive work on the quantized version of classical strategic 2-2 games, most of them are based on the protocol specified in [5] . It requires application of an entanglement (unitary) operator 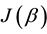(where β is a real parameter), which acts on a non-entangled 2-qubit (pure) state resulting in an entangled state whose degree of entanglement is measured by its von-Neumann entropy. A desired property of is that is a continuous function of β that varies (preferably monotonically) between 0 (no entanglement) and (maximal entanglement). The reason for exploring partially entangled 2-qubit states is that the existence of pure strategy Nash equilibrium in the 2-2 quantum game crucially depends on the degree of entanglement (see below).

Controlling the entropy by a single parameter that all values between 0 and are obtained is referred to here as single parameter completeness. The relevance of this problem to quantum information in general is quite obvious. An important procedure in quantum information is to design a quantum gate that generates Bell states [1] [2] . The gate, operating on a non-entangled two qubit state, results in a Bell state that is maximally entangled. Therefore, designing the gate that does the job for an arbitrary two quNit state resulting in an entangled state whose degree of entanglement is controlled by a single parameter should be very useful.

3. Classical Commensurability

Another practical property required from is that it can easily be constructed from the classical strategies. In a 2-2 game, the classical strategy of a player is, and an appropriate construction is then

. Its action on an unentangled 2-qubit state (e.g) yields,

, (1)

where the left (right) factor in the Kronecker product refers to player 1 (2). In this way, appears in a Schmidt decomposed form, enabling an easy computation of the corresponding entanglement entropy of the 2-qubit state on the RHS as

. (2)

Thus, is a continuous function of and gets all values in, namely as defined in Equation (1) satisfies single parameter completeness. Other properties (of less significance) are that is

periodic with period, symmetric about the mid-point, with and.

The entangler defined in Equation (1) has a property referred to as classical commensurability,

. Following the rules of the game specified in [5] , it means that players in a 2-2 quantum game can, if they wish, use their classical strategies as a special case and if they do so, they collect the corresponding classical payoffs. In most cases, however, the classical strategies do not constitute a pure-strategy Nash Equilibrium (NE) (defined below). Generically, as we explain below, classical commensurability does not hold for [10] .

4. The Present Work

In the present work we examine the issue of constructing for a quantum game based on a 2- players-N-strategies classical game. We suggest a natural extension of Equation (1) for constructing an operator that turns a non-entangled 2-quNit state into an entangled one. For the corresponding von- Neumann entropy varies continuously between 0 and so that single parameter completeness is satisfied. Unfortunately, this method does not work for because in that case. To alleviate this deficiency we suggest another method (albeit less intuitive) to design that satisfies single parameter completeness for any. In what follows we will first introduce the classical 2-3 game using quantum information language and formulate its quantum version (extension to is straightforward). Most of this introductory exposition is well established and is included here merely for self consistence. Then, in the second step, we shall address the issue of constructing.

5. Two-Players-Three-Strategies Classical Games: Trits

Consider a two-players classical game with three strategies for each player. For example, two prisoners may have three options, marked as three values of a trit, and for Confess, Stay quiet or Don’t confess. The two prisoner “system” can be found in nine two-trit states, , , corresponding to the nine entries of the game table. The protocol of the classical game with 2-players and 3-strategies is as follows: The referee (judge) calls the players (prisoners) and tells them he assumes that they are in an initial two-trit state meaning (C,C) namely both confess. He then asks them to decide whether to leave their respective trit state as it is on or to change it either to (meaning S) or to (meaning D). These replacement operations (specified explicitly below) are the players’ classical strategies. If the initial state suggested by the referee is the strategies of the two players include (leaving the trit at as it is), (swapping of and namely, replacing C by S) and (swapping and namely replacing C

by D). These three operations generate the group of permutations of three elements. Explicitly,

We shall indicate below that a quantum strategy is a gate represented by an matrix. A reasonable requirement for the procedure of “quantizing” a classical game is that the classical strategies obtain as special case of the quantum ones. For that purpose we need to construct a representation of the permutation group in terms of unitary matrices with unit determinant. This can be achieved by choosing

. (3)

For example, suppose player 1 and 2 choose respective strategies and. This brings the system into a state. Then the respective payoff of player, will be, where is the payoff of player at entry of the game table.

6. The Analogous Quantum Game: 1 and 2 Quirt States

We now briefly explain the structure of the corresponding quantum game. Its main ingredients are qutrits, quantum strategies, and entanglement operations. Both versions use the same game table but the payoff rules are somewhat different.

Consider the three dimensional Hilbert space with orthonormal basis vectors, and. A qutrit is a vector of unit norm,. A general 2-qutrit state is a normalized vector in,

(4)

A maximally entangled two-qutrit state is written as

, (5)

given in a Schmidt decomposed form. Its entanglement degree is measured by the von Neumann entropy

.

7. 2-3 Quantum Game Strategies

A strategy of a player in a 2-3 quantum game is an matrix by which he operates on his qutrit (that is a quantum gate). A strategy depends on eight Euler angles. The explicit expression of in terms of Gellman matrices, is well known. For quantum game theory, a practical parametrization of is suggested in [10] .

8. 2-3 Quantum Game Procedure

The referee suggests an initial non-entangled two-qutrit state (e.g, the analog of the classical two trit state). Before letting the players apply their quantum strategies, the referee operates on with a unitary operator such that is entangled (otherwise the game remains classical). Construction of the operator (our central goal) is detailed below. At this stage of the game, the players apply their respective strategies. Finally, the referee applies the operator, leading to the final state

, (6)

where is the octet of 8 Euler angles defining the matrix (that is the strategy of player). The payoff of player is given by

, (7)

where are the payoffs at entry of the classical game table. Like in the classical game, each player choses a strategy with the goal of maximizing his payoff.

9. Pure Strategy Nash Equilibrium (NE)

Because the set of 8 Euler angles uniquely determines the player’s strategy, a pure strategy NE in the 2-3 quantum game is a pair of strategies (each represents 8 angles) such that

(8)

The question of whether pure strategy NE exists in a 2-2 quantum game and its relation to the degree of entanglement (controlled by) has been discussed in numerous works [11] - [17] . In brief, if there is NE in the classical game that is not Pareto efficient [18] , then there is a critical value above which there is no pure strategy NE in the quantum game. As approaches from below, the respective payoffs in the quantum game at NE approach the Pareto point of cooperation [13] [17] . This is the main reason why, right from the onset, we stress the relevance of partially entangled 2-quNit states where.

10. Absence of Classical Commensurability

We now explain why in a 2-3 quantum game there is no classical commensurability [10] . Recall that classical commensurability means that if the players use classical strategies they respectively get their classical payoffs. For a classical strategy we have. From Equation (6) it means that should commute with all outer products of the classical strategies. If the initial state is the 9 outer products of classical strategies are, where (see Equation (3)). Classical commensurability then requires

. (9)

This is possible only if J is a function of where A is a matrix satisfying , and is not just a multiple of. But this is impossible because and generate an irreducible representation of the permutation group and hence, according to Schure’s lemma is just a multiple of. These arguments naturally hold for any.

11. Designing the Entangler

The main result of the present study concerns the analysis and construction of an entanglement operator for. We carry it out for and then extend it straightforwardly to any. For we require that yields an entangled 2-qutrit state with specifying the degree of entanglement that achieves any value between 0 and. Following the 2-2 game framework specified in Equation (1), we try to construct J by exponentiating a combination of classical strategies. In order to get the “diagonal” 2-qutrit states and from the qutrit state, we have to operate on with. Therefore, we define

. (10)

Calculation of the exponent yields

. (11)

Maximal entanglement obtains when the absolute values of all three coefficients are equal, namely

. (12)

Here raises monotonically from 0 to its first maximum, hence we have found the desired entanglement operator that satisfies single parameter completeness. Figure 1(a) displays the von Neumann entropy of the entangled 2-qutrit state (11) as function of. Here again it possesses other properties, namely

is a periodic function of with period and it is symmetric about the mid-point where it has a local minimum. It has two maxima for where it equals. Inspecting Equation (10),

we see that, in quantum games, the entanglement is not obtained in terms of spin rotations but, rather, in terms of permutation exponentials that are SU(3) matrices (for these are the same).

12. Extension to Arbitrary N

Let denote the matrix representing the permutation and let, be an unentangled 2-quNit state. To get an entangled state from we define and assert that

. (13)

To proceed, let us define the absolute value squared of the coefficients

. (14)

It is easy to verify that: 1); 2); 3) is periodic with pe-

riod and symmetric about the mid-point. The entanglement entropy is

. (15)

Maximal entanglement obtains for that is the solution of the equality

. (16)

For the two solutions are specified in Equation (12). For, there is a single solution at, as shown in Figure 1(b). Thus, for we have achieved our goal of constructing an entanglement operator such that the degree of entanglement of the 2-quNit state varies continuously reaching all values in the interval, so that single parameter completeness is satisfied.

For there is no solution of Equation (16), and maximal entanglement is not achieved. It might be argued that 2-N quantum games with are much rarer than those with smaller N but we believe that the construction of that satisfies single parameter completeness also for is useful in other areas (outside the ballpark of quantum game theory), so we carry it out for the sake of completeness.

The method suggested here is not based on permutation exponentials as in Equation (10). It consists of the following steps.

1) Assume a lexicographic order of the basis states such that the diagonal states appear in

the first N places. Choose a unitary matrix of the form where R is an uniray matrix with equal first column elements and is the unit matrix. The problem is

then reduced to the dimensional subspace spanned by. By construction,

that is a maximally entangled state.

2) Diagonalize as where is the matrix of eigenvectors of, and

is the diagonal matrix of (unimodular) eigenvalues of with eigenphases.

(a) (b)

Figure 1. von Neumann entropy defined in Equation (15), for the 2-quNit state defined in Equation (13): (a), (b). varies continuously reaching all values in the interval, so that single parameter completeness is satisfied. Here is periodic with period.

3) Now consider the matrix

. (17)

By construction, and. Hence, the state is partially entangled. Since it is given in a Schmidt decomposed form, the corresponding von Neumann entropy is easily calculable. is continuous in with and, namely single parameter completeness is satisfied. Generically, the eigen phases are not rational multiples of so that is not periodic, but this lack of periodicity is of no special significance.

13. Illustration for

A convenient way to build an appropriate unitary matrix is to start from a simple non-singular matrix and then orthogonalize it within the Grahm-Schmidt procedure. For example,

Proceeding with the list of steps prescribed above we can easily construct and compute the von Neumann entropy of the state upon which the players apply their strategies according to the game protocol specified in Equation (6). The result is given in Figure 2.

As explained in the figure’s caption, the degree of entanglement is controlled by a single parameter and is a continuous function of reaching any value in the interval. Thus we have achieved our goal of constructing an entangler that turns a non-entangled 2-quNit state into an entangled one given in a Schmidt decomposed form with single parameter completeness satisfied.

14. Summary

In conclusion, we suggest two methods to design an entanglement operator that turns a non-entangled

(a) (b)

Figure 2. von Neumann entropy for 2-quNit state, where is defined in Equation (17). (a), (b) correspond to. By constructing, and (horizontal lines). Since is a continuous function of it reaches any value in the interval. That is, single parameter completeness is achieved for.

2-quNit state to a partially entangled state whose von Neumann entropy is fully controlled by a single real parameter. The first method is intuitively clear and simple, based on exponential of classical strategies, Equation (10), and results in the von Neumann entropy, as displayed in Figure 1. This method does not work for because the resulting entropy does not reach the maximally entangled value. For that reason we suggest another method that is somewhat less transparent but works for any N. The resulting entropy as function of is displayed in Figure 2.

The entangler constructed here generalizes, in two directions, the familiar quantum gate used in quantum information science to create Bell states from non-entangled two-qubit state. First, it is applicable to any two-quNit state, and second, it contains a single continuous parameter that controls the degree of entanglement of the resultant state.

Acknowledgements

I would like to thank Oscar Vollij for his excellent course in (classical) game theory. Discussions with Eytan Bachmat, Hosho Katsura, Rioichi Shindou, Doron Cohen and Yehuda Band are highly appreciated. This work is partially supported by grant 400/2012 of the Israeli Science Foundation (ISF).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Nielsen, M.A. and Chuang, I.L. (2000) Quantum Computation and Quantum Information. Cambridge University Press, Cambridge, p 26, Fig. 1.13.
[2]	Band, Y.B. and Avishai, Y. (2013) Quantum Mechanics with Application to Nanotechnology and Information Science. Academic Press, Waltham, p 217.
[3]	Goldenberg, L., Vaidman, L. and Wiesner, S. (1999) Quantum Gambling. Physical Review Letters, 82, 3356. http://dx.doi.org/10.1103/PhysRevLett.82.3356
[4]	Meyer, D. (1999) Quantum Strategies. Physical Review Letters, 82, 1052-1055. http://dx.doi.org/10.1103/PhysRevLett.82.1052
[5]	Eisert, J., Wilkens, M. and Lewenstein, M. (1999) Quantum Games and Quantum Strategies. Physical Review Letters, 83, 3077-3080. http://dx.doi.org/10.1103/PhysRevLett.83.3077
[6]	Flitney, A.P. and Abbott, D. (2002) An Introduction to Quantum Game Theory. Fluctuation and Noise Letters, 2, R175-R187. arXiv: quant-ph/0208069. http://dx.doi.org/10.1142/S0219477502000981
[7]	Piotrowski, E.W. andSlaadkowski, J. (2003) An Invitation to Quantum Game Theory. International Journal of Theoretical Physics, 42, 1089-1099. http://dx.doi.org/10.1023/A:1025443111388
[8]	Landsburg, S.E. (2004) Quantum Game Theory. Notices of the American Mathematical Society, 51, 394-399.
[9]	Iqbal, A. (2004) Studies in the Theory of Quantum Games. Ph.D thesis, Quaid-i-Azam University, Islamabad, 137 p. arXiv:quant-phys/050317.
[10]	Sharif, P. and Heydari, H. (2014) Quantum Information and Computation, 14, 0295.
[11]	Landsburg, S.E. (2011) Nash Equilibria in Quantum Games. Proceedings of the American Mathematical Society, 139, 4423-4434. arXiv:1110.1351.
[12]	Benjamin, S.C. and Hayden, P.M. (2001) Comment on “Quantum Games and Quantum Strategies”. Physical Review Letters, 87, Article ID: 069801. http://dx.doi.org/10.1103/PhysRevLett.87.069801
[13]	Du, J., Li, H., Xu, X., Han, R. and Zhou, X. (2002) Entanglement Enhanced Multiplayer Quantum Games. Physics Letters A, 302, 229-233. http://dx.doi.org/10.1016/S0375-9601(02)01144-1
[14]	Du, J., Xu, X., Li, H., Zhou, X. and Han, R. (2002) Playing Prisoner’s Dilemma with Quantum Rules. Fluctuation and Noise Letters, 2, R189. http://dx.doi.org/10.1142/S0219477502000993
[15]	Flitney, A.P. and Abbott, D. (2003) Advantage of a Quantum Player over a Classical One in 2 × 2 Quantum Games. Proceedings of the Royal Society A, 459, 2463-2474. http://dx.doi.org/10.1098/rspa.2003.1136
[16]	Flitney, A.P. and Hollenberg, L.C.L. (2007) Nash Equilibria in Quantum Games with Generalized Two-Parameter Strategies. Physics Letters A, 363, 381-388. http://dx.doi.org/10.1016/j.physleta.2006.11.044
[17]	Avishai, Y. (2012) Some Topics in Quantum Games. MA Thesis in Economics, Ben Gurion University, Beersheba, 96 p. arXiv:1306.0284. (Submitted on August 2012 to the Faculty of Social Science and Humanities at the Ben Gurion University).
[18]	Osborne, M.J. and Rubinstein, A. (2011) A Course in Game Theory. The MIT Press, Version: 2011-1-19. Cambridge, Massachusetts, London, England.