Probabilistic Model of Cumulative Damage in Pipelines Using Markov Chains ()
1. Introduction
Throughout Mexico, there are approximately 54,000 kilometers of terrestrial pipeline in operation, transporting crude oil, natural gas, sour gas, sweet gas, gasoline, diesel, and other refined products. In addition, there are 2000 kilometers of underwater pipeline. Almost half of pipeline has been operating for more than 30 years and, in spite of continual maintenance, inspection and patrolling works, problems caused by corrosion, damage by third parties, operation and design mistakes that may lead to system failure are present. Failures of these pipeline systems constitute significant financial losses and, in the worst scenario, loss of human lives and damage to the environment. Failure may be due to several causes and may occur in a small area of the pipeline; however, to identify significant factors contributing to failure in the pipeline is possible. Accidents due to corrosion in pipelines transporting hydrocarbon are the most frequent.
Corrosion is damage to materials caused by ions transportation and due to potential difference in the material itself or between the material and its surrounding environment. It is an irreversible interfacial reaction, generally of a metal, with its surrounding environment which damages or modifies its properties. Corrosion causes loss in mechanical resistance properties of the material, resulting in changes of structures and components geometry; therefore the material loses the function for which it was intended, causing: 1) direct losses due to change in corroded tubular structures; 2) indirect losses resulting from loss of production due to temporary suspension of productive systems and facilities and pollution of goods generated; 3) loss of wellbeing and human lives; 4) efficiency loss; and 5) increase of exploitation costs.
Corrosion is of major interest since the loss of metal invariably implies a reduction of the structural integrity of the pipe and an increase in the risk of failure. The two most significant factors involved in the corrosion process are the type of material and the environment. The environment includes conditions impacting on the internal and external walls of the pipe. Since most pipelines undergo various environmental conditions, the assessment must allow proper sectioning or consideration of each type of environment in each given segment. In addition, corrosion may be divided into uniform and localized corrosion. Uniform corrosion is that which develops at the same speed on all of the surface of the material, while localized corrosion refers to an accelerated attack on a specific superficial position, generally due to separation of anodic and cathodic areas, and is caused by inequalities of the structure or composition of the corroding material or differences in the environment. Pitting corrosion is a special type of localized corrosion, defined as a very localized attack on passive metals, causing very narrow and deep cavities.
The study of corrosion has been mainly based on deterministic approaches, particularly on the electrochemical corrosion theory; however, localized corrosion cannot be explained without statistical and stochastic points of view due to high dispersion of laboratory and field data (see ref. [1] and ref. [2]). Assessment of the integrity and reliability of pipelines has been studied in various ways in recent years and risk and reliability analyses have been applied to determine failure probabilities.
A formal analysis is carried out using reliability tests in the risk of failure assessment. Thus, from a structural point of view, reliability or probability of success is the probability of a structure, an element or structural element satisfying the limit and service conditions for which it was intended. In this manner, the risk of failure assessment on ducts based on mechanical or structural reliability methods is a better approach in assessing safety, providing an analytical tool which allows the assessment of risk with more reasonable and verifiable methods that may always be improved. Reliability methods provide elements to design a structural system and are also used to know the current conditions of a system. This is very important when making decisions regarding maintenance, repair or substitution of structural elements in the system, in order to take the structural system back to the required safety level specified.
Cumulative damage is the irreversible accumulation of damage throughout the life of the element, which eventually results in degradation and failure. A stochastic process is a mathematical model of a dynamic process which evolution in time is governed by probabilistic laws (see ref. [3]). In probability theory, there were no general procedures or particular schemes to solve this type of problems. This brought a new general theory of random processes to study these problems. Any knowledge about the states of a system will lead us to study the type of stochastic processes called process without further effect or, by analogy, Markov chains or processes. Andrei Andreyevich Markov was a Russian mathematician known for his works on theory of numbers and probabilities theory. The model proposed assumes a finite and discrete state of time using Markov processes, which assumes that probability of what will happen in a given instance will depend exclusively on the immediate previous past.
J.L. Bogdanoff and F. Kozin started their study of Markov’s cumulative damage models in 1978. In the beginning, there was doubt about its usefulness in engineering and its practical value. However, this negative point of view changed, since its potential application field in the cumulative damage phenomenon is vast. These models have been capable of describing and successfully analyzing life data of various phenomena, including fatigue, growth of cracks due to fatigue, corrosion, and change of properties of the material, among others. In addition, these models have provided profound knowledge about many interesting problems in engineering (see ref. [3]). Models of phenomena may be deterministic or probabilistic. The interest of above-mentioned researchers is focused on the evolution in time under cyclic uses, damage due to fatigue, crack lengths, and loss of material. A probabilistic model is proper for cumulative damage phenomena in which uncertainties to estimate the mean life may not be ignored. Localized corrosion is known for showing high variation in measurable parameters such as corrosion rate, maximum pitting depth, and time to perforation, among others. Variation in results is derived from the influence of heterogeneities on the metal surface throughout pitting development and variations in the corroding environment throughout time. All these facts suggest that randomness is an inherent and unavoidable feature of pitting corrosion throughout time; therefore, stochastic models are a better choice for describing pitting corrosion than deterministic models are (see ref. [1]). Provan and Rodríguez used a non-homogeneous Markov process to model growth of pitting depth without taking into account the generation process. This model aims at describing the growth of pitting as a function of time of exposure, considering a discrete space of states of possible pitting depths. They compared the estimated results with experimental data reported for aluminum and directed their own experiences in pitting corrosion towards stainless steels (see ref. [4]). H.P. Hong considered pitting corrosion as a combination of two stochastic processes: he modeled the generation of the pitting process as a Poisson process and the propagation of depth as a Markov process (see ref. [5]). The probability distribution of pitting corrosion depth and probability of time to failure are obtained by combining both processes. To use the method, examples based on experimental data were developed. In this work, the transition intensity used to describe growth of a specific depth in the homogeneous Markov process depends on the total number of states used and does not define the number of optimal states to describe a given set of experimental data (see ref. [5]). Valor and his research team developed a stochastic model to simulate localized corrosion. Localized corrosion was modeled as a non-homogeneous Poisson process in which the time of induction to pitting initiation was simulated as carrying out a Weibull process. To simulate growth of pitting they used a non-homogeneous Markov process. The model proposed is validated using data from published experiments on localized corrosion (see ref. [6]). A stochastic prediction model of damage evolution due to corrosion in active sites, applicable under professional practice conditions, is presented by J.L. Alamilla and E. Sosa (see ref. [7]). It uses integrity and structural reliability analyses. Damage of a material and its evolution are determined by the damage state in a given time instant and a damage occurrence rate. To achieve this, the probability density function of the pitting corrosion damage depth of the system is estimated. Its application depends on the quantity of inspection reports available. Two scenarios are presented: when there is one inspection report and when there are two inspection reports. In the latter scenario, there is variation regarding whether defects may be identified in the two inspections or not (see ref. [7]). In this work, localized corrosion due to internal pitting is studied, since depending on a lower number of factors than external corrosion, simpler mathematical models may be developed (see ref. [8]). Corrosion analyzed in this work is focused on loss of pipe metal. In addition, a probabilistic model of cumulative damage due to corrosion is carried out. Cumulative damage reduces reliability as time increases. Keeping high reliability levels, carrying out inspections, repairs, partial replacements, and keeping proper operation conditions may increase the cost of the system’s life cycle. This study is useful because it creates a tool that enables the prediction of the corrosion state in a giveninstant of time, in order that resources for inspection, maintenance and repair programs may be optimized.
We set as an objective to establish a methodology based on a probabilistic damage model and Poisson and Markov stochastic processes that allow describing and predicting the state of corrosion in terrestrial pipelines for transport of hydrocarbons in a given period of time.
For such purpose, we proposed to statistically analyze the data on pipeline inspection; to define the limit states of variable depth of corrosion defect; to determine the starting and transition probability of the model; to assess corrosion of pipelines transporting hydrocarbons in several instants of time; and to calculate expected time to failure.
2. Stationary Stochastic Model of Cumulative Damage
In our model of cumulative damage in pipelines using Markov chains, it is assumed that: 1) seriousness of the service cycle is repetitive and constant (that is, it is considered that anything that happens in a service cycle occurs in every other cycle); 2) damage states are discrete and called
(failure); 3) cumulative damage in a service cycle depends only on the service cycle and the damage state at the beginning of the cycle; and 4) damage may only be increased in a service cycle, from the state occupied at the beginning of the cycle, to the state of a higher unit.
Time x is made discreet by the first assumption, for that reason
Permissible damage states have been made discreet in the second assumption, therefore, the model has finite (discrete) damage and time states. As for the third assumption, the model does not mention anything about quantitative details of what happens within a service cycle. This third assumption is Markov’s, which is damage accumulation in a service cycle, only depending on the corresponding service cycle and the damage state in which the cycle started. In the model, to know how the starting damage was achieved is irrelevant. When state b is reached, withdrawal or failure occurs. Thus, state b is an absorbent state and
. The fourth assumption implies that it must be transitory since, once damage moves from a state to the next one, it never goes back to the immediately previous state.
This version of the cumulative damage model is a stationary Markov process, with discrete time and finite states. The cumulative damage mechanism is of the unit jump type, depending on the state.
Let
be the random variable defined as the state occupied by damage in time
. The starting probability distribution
over damage states in
are specified by vector line (1 × b):
, where
y
. It should be noted that in no case does it start at failure state, since
. π’s creates a mass function with
probability.
The constant probability P transition matrix is associated if each service cycle has constant seriousness; in addition, based on the fourth assumption, it is only possible to pass from a state to a higher state, therefore:
(1)
where
and
. pj is the probability to remain in state j for a step; qj is the probability that, in a step, damage goes from state j to state j + 1. It may be observed that for (1) all damage states
are transitory and state b is absorbent.
Let
be the damage state occupied in time x, and let:
, be probability that damage occupies state j at time x. Since
and
, px(j) creates a probability mass function in time x in damage states
. Now, using vector line (1 × b):
to represent this probability mass function and, based on Markov’s chain theory:
(2)
where P0 = I and I is the identity matrix (b × b).
A graphic view of Equation (2) is that of a set of vertical bars representing px(j), where x is on the time axis at regular intervals. When x increases, the probability mass is displaced from lower to higher states and, gradually, deviated to state b. In the last case, all masses accumulate in state b. Its final structure depends on p0 and pj. It should be noted that px(b) is a distribution function accumulated in time x, since the limit when x ® ¥ is px(b) = 1, as all masses in the last case come to state b and stay there. Probability px(j) is the probability that
is in state j in time x.
Given p0 and P, in (2)
is calculated and it is known that the accumulated distribution function of time Wb to absorption in state b (with pb = 1) is px(b).
becomes time to failure in the cumulative damage model. Cumulative distribution function of
is given by:
(3)
t reliability function
es:
Failure
rate function
is:
The mean and variance of Wb are, respectively:
and
The probability that damage
is in state j in time x is determined by px(j):
and the cumulative distribution function of Dx is:
. Its mean and variance are given by:
and
Thus, Equation (2) gives results required to determine basic probabilistic data for cumulative damage in which failure occurs upon arriving at state b. This equation is easy to program using standard routines to multiply matrices. If advantage of P’s shape is used, calculations may be efficiently managed.
For this case,
and
, cumulative damage process starts in state 1 with x = 0. Random variable
, is time to failure in state b since it started in state 1 in x = 0. Geometric transformation of cumulative distribution function
de
is:
(4)
and the transformation of the probability mass function
is:
(5)
Inversion of these two transformations is direct. If we assume that:
, then:
(6)
where:
(7)
It should be noted that:
(8)
since a unit jump model may not reach state b from 1 in less than (b − 1) n-steps. Therefore,
satisfy certain relationships implied in (8). Equation (6) and Equation (7) are valid for
.
Inversion of (5) gives the probability mass function
of W1,b: and it is found using the technique used to obtain (6):
(9)
This equation may also be obtained noticing that:
(10)
is equal to zero for .
.
The mean and the first central moments of W1,b are obtained from the characteristic function of (5), using the differentiation technique. These are:
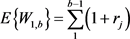

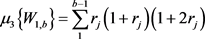
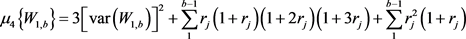
where
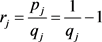 and
and 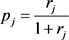 (11)
(11)
The reliability function 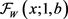 corresponding to the cumulative distribution function of (6) is:
corresponding to the cumulative distribution function of (6) is:
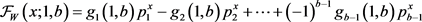 (12)
(12)
The risk function 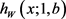 is obtained using (9), (10) and (12), these being:
is obtained using (9), (10) and (12), these being:
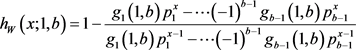 (13)
(13)
W1,b is time required to reach state b since it started with state 1 at time x = 0. Given that:
 (14)
(14)
where Tj’s are independent and, upon adding Tj’s characteristic function, we obtain:
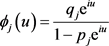 (15)
(15)
we have that W1,b’s characteristic function is:
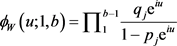 (16)
(16)
If we substitute 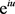 with z, we obtain the geometric transformation of the probability mass function of W1,b given in (17)
with z, we obtain the geometric transformation of the probability mass function of W1,b given in (17)
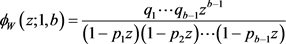 (17)
(17)
This formula is the same as the one obtained in (5) using (4).
Let us assume now that  is a permutation of
is a permutation of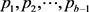 , then (4) becomes:
, then (4) becomes:
![]() (18)
(18)
This equation may be inverted to find ![]() and obtain exactly the same equation as that defined in (6); for this reason, it may be said that there is
and obtain exactly the same equation as that defined in (6); for this reason, it may be said that there is ![]() permutations of
permutations of![]() . Thus, there are
. Thus, there are ![]() models with the same cumulative distribution function
models with the same cumulative distribution function ![]() of
of![]() . In order to know how these models are different from each other, the notion of sample function mean must be introduced.
. In order to know how these models are different from each other, the notion of sample function mean must be introduced.
Time used in state j is random variable![]() , whose characteristic function is given in (15). It is found that this is the expected time value used in each state, and it is given by:
, whose characteristic function is given in (15). It is found that this is the expected time value used in each state, and it is given by:
![]() (19)
(19)
In the succession of the mean time used in each state, the adjacent points are linked with line segments; their segmented curve is the mean of the sample function, since it shows behavior of the sample function mean. Actually, the family of sample functions creates a propagated cloud coming from state 1 at![]() . Mean simple function is the position of the mean of this cloud in various states. Time in which the sample function mean reaches b is, in case of the unit jump,
. Mean simple function is the position of the mean of this cloud in various states. Time in which the sample function mean reaches b is, in case of the unit jump,![]() .
.
Now, it is possible to know the difference between models. While all ![]() models have the same
models have the same![]() , each has a different sample function mean. This is a very important point, since it explains that the cumulative distribution function
, each has a different sample function mean. This is a very important point, since it explains that the cumulative distribution function ![]() of
of ![]() does not define the evolution of the cumulative damage process.
does not define the evolution of the cumulative damage process.
Let us consider the set of cumulative distribution functions ![]() for
for![]() . This set depends on rj’s order. If the set is specified, this defines, in a unique manner, the evolution of the cumulative damage process even when in each
. This set depends on rj’s order. If the set is specified, this defines, in a unique manner, the evolution of the cumulative damage process even when in each ![]() set it is the same.
set it is the same.
The above observations apply to the ![]() case. Let us assume that
case. Let us assume that ![]() are different from zero or one, where
are different from zero or one, where![]() . Therefore,
. Therefore, ![]() may not be reordered without changing
may not be reordered without changing![]() , since
, since ![]() depends on
depends on ![]() order for
order for![]() . However,
. However, ![]() may be reordered without altering
may be reordered without altering![]() . Thus, unless all
. Thus, unless all ![]() for
for ![]() are different from zero,
are different from zero, ![]() does not specify in a unique manner the cumulative damage process of the model.
does not specify in a unique manner the cumulative damage process of the model.
The most important points of this simple stationary unit jump model with probability transition matrix given by (1) are:
· starting damage distribution may be incorporated into the model;
· variable seriousness in service cycles may be incorporated into the model, changing transition P matrices in time;
· explicit shapes for![]() ’s moments may be obtained;
’s moments may be obtained;
· ![]() ’s order does not change the cumulative distribution function of
’s order does not change the cumulative distribution function of![]() ; and;
; and;
· knowing the cumulative distribution function ![]() does not determine the evolution of
does not determine the evolution of![]() .
.
3. Application of the Model with Inspection Data
Below some observations are shown on the bases of the cumulative damage model:
· time is discrete ![]() Each x represents an actual time interval;
Each x represents an actual time interval;
· damage states are finite and discrete, called ![]() (failure). Each state is represented by certain thickness of the pipeline’s wall;
(failure). Each state is represented by certain thickness of the pipeline’s wall;
· damage states are finite and discrete, called ![]() (failure). Each state is represented by certain thickness of the pipe’s wall;
(failure). Each state is represented by certain thickness of the pipe’s wall;
· the starting damage value may be random, but in this work it is considered that the pipeline has no damage at the beginning, and because of that the probability to be in state 1 at time x = 0 is one, that is, the starting damage vector is![]() ;
;
· the state in which failure occurs is given by![]() , that is, failure occurs in the last state, state b, not before that, and;
, that is, failure occurs in the last state, state b, not before that, and;
· cumulative damage in an x time step is constant and does not decrease.
Data of internal pitting corrosion depths in a 155,500.34 m long, 5.6 mm thick diesel-transporting pipeline were obtained. Inspection reported 96 corrosion pits. Upon carrying out a statistic analysis, their histogram was obtained, where each class interval of the histogram is considered a damage state of the model.
Probability of each interval is obtained from dividing the number of defects of each interval into the total number of defects, therefore obtaining probability vector![]() . Probabilities obtained from the probability density function are shown in Table 1.
. Probabilities obtained from the probability density function are shown in Table 1.
In order obtain transition probabilities, equations resulting from developing Equation (2) for times ![]() are used. The starting probability vector
are used. The starting probability vector ![]() is multiplied times the P transition matrix described in (1), raised to the power of x. Upon equaling probabilities of Table 1 with equations involving p1, p2, p3, p4, p5, p6, and p7 we have:
is multiplied times the P transition matrix described in (1), raised to the power of x. Upon equaling probabilities of Table 1 with equations involving p1, p2, p3, p4, p5, p6, and p7 we have:
![]()
![]()
upon solving above equations, the values of Table 2 were obtained.
As can be observed, in this case it is not possible to find all the values of pj with the histogram, since its shape leads to numerical problems.
A solution to this problem is to calculate the cumulative distribution function of data, to make an adjustment and obtain probabilities of each interval. Figure 1 shows cumulative distribution obtained from data.
Several adjustments were made to data with various probability functions. Figure 2 shows the various adjustments that were made. Adjustments with Lognormal and Birnbaum-Saunders distributions were found to allow solving numerical problems (see Birnbaum and Saunders, ref. [9]). Figure 3 and Figure 4 show a comparison of histograms with both adjustments. The Birnbaum-Saunders distribution, also known as the fatigue life distribution, is a probability distribution
![]()
Table 1. Probabilities of each state at time x = 7.
![]()
Table 2. Transition probabilities for P matrix at time x = 7.
![]()
Figure 1. Empirical cumulative probability distribution function.
![]()
Figure 2. Adjustment to the cumulative probability distribution function curve.
extensively used in reliability applications to model failure times (see Birnbaum and Saunders, ref. [9] ).
The Lognormal distribution was chosen to present the probability distribution function of corrosion pitting. At first sight, differences may be observed between the histograms and the probability distribution functions; however, probability has a theory to know if the set of data resulting from sampling a random variable
![]()
Figure 3. Comparison between measured probabilities (heavy) and with Lognormal adjustment.
![]()
Figure 4. Comparison between measured (heavy) probabilities and with Birnbaum-Saunders (light) adjustment.
may be represented with a certain distribution function. Based on the above, it is important to know if data actually adjust to the distribution proposed with an acceptable reliability level. To this end, a Kolmogorov-Smirnov hypothesis test was carried out. The adjustment proposed passed this test with a 1% significance level, and so it is possible to use the Lognormal distribution for the following calculations.
Figure 5 and Figure 6 show the evolution of transition pj probabilities and the rj relationship with both adjustments.
![]()
Figure 5. p and r variation (Lognormal).
![]()
Figure 6. p and r variation (Birnbaum-Saunders distribution).
The values of the probability to be in each state at time x = 7 from the histogram adjusted with Lognormal function are shown in Table 3.
Again, the procedure to find transition probabilities is carried out. Equations resulting from multiplying the starting state times the transition matrix raised to the power of x = 7 is vector
![]()
Upon equaling each px(j) to probability numerical values and solving equations, it is possible to find pj. Table 4 shows such values. Table 5 shows rj values,
remembering that![]() .
.
It can be observed that, with the Lognormal adjustment, it is possible to find transition probabilities up to x = 7. Until now, necessary data has been obtained up to inspection time. Probabilities to fill the transition matrix and r ratio have been obtained. This data is essential to know the time to failure expected, since the next step is to observe and assess the trends of probabilities found to extrapolate data until failure. A way to use data obtained up to inspection time to obtain the probabilities of transition to failure is by using an equation that is a function of a parameter and adjusted to data. In this way, probabilities after inspection may be known.
Taking into account the shape of qj evolution for various states, the following equation is proposed:
![]()
where Yq is the lowest value of q, Iq is the state of the lowest value of q, and λ is a parameter adjusted to data.
Since the thickness of the pipe under study is 5.6 mm and the class intervals of the histogram are 0.0643, it may be deducted that the number of b states to failure must be:
![]()
Table 3. Probabilities of each state at time x = 7.
![]()
Table 4. Transition probabilities for P matrix at time x = 7.
![]()
where t is the thickness of pipe equal to 5.6 mm and ![]() is the class interval equal to 0.0643 mm .
is the class interval equal to 0.0643 mm .
With data known up to the inspection time, λ’s value is found by calculating the mean square error. λ’s value minimizing error is λ = 0.055. Knowing this value, it is possible to calculate qj up to failure. Figure 7 shows a comparison of qj measured from data and that is calculated with λ’s function. It may be seen that there is good adjustment of the function. In this way, qj has been calculated up to failure. Figure 8 shows comparison of rj variation calculated as a function of λ and the one calculated from data.
With the above adjustments, it is possible to obtain all the transition probabilities of passing from one state to another one, considering all states, up to failure.
Now that we have the transition matrix, the cumulative distribution function of Dx is calculated.
![]()
and the mean and variance of Dx are given by:
![]() y
y![]()
Figure 9 shows the cumulative damage distribution function with actual data of the pipe under study, where it can be seen that it is complied with, that is to say:
![]()
Figure 7. Comparison of qj calculated from data (measured) and λ’s function (modeled).
![]()
Figure 8. Comparison of rj calculated as a function of λ (modeled) and calculated from data (measured).
![]()
Figure 9. Cumulative distribution function ![]() and
and ![]() of the pipe under study.
of the pipe under study.
![]()
since a unit jump model may not reach state b from 1 in less than b – 1 step. Based on the above, the distribution curve starts to be different from zero in state 79. It may be seen that it quickly rises and that probability of time to failure being lower or equal to 120 is one, which means, at that time, the system has failed.
It may be observed that the failure function starts from zero, at the same time as the distribution function, since the pipeline is considered to have no damage at the beginning, and it raises until becoming constant at a 0.3 value. Based on the above, it may be said that the probability that pipeline fails, if it has worked in a given period, is low. Figure 10 and Figure 11 show the mean and variance of the pipe under study, respectively.
The mean shows the damage state value expected for each step of time x. In
![]()
Figure 10. Mean of Dx of the pipe under study.
![]()
Figure 11. Variance of Dx of the duct under study.
the first stage, variation is not linear, but from state 20, variation of the mean is constant. Variance gives us the average of squares of deviations regarding the mean. In this case, it increases until it becomes constant in a value lower than 30, which shows that there is not a high variation and that the model is reliable. To know time to failure of the pipe, time used in state j is the random Tj variable, it being possible to apply Equation (19) with the rj until failure, in order to know the mean time used in each state, as well as its succession. Figure 12 shows the curve representing the mean of the sample function![]() .
.
In order to prove and have an idea of how the theory works, simulations were carried out using Monte Carlo simulations. That is, a uniform distribution was used to obtain random times in each state, following a geometric distribution. The procedure includes simulating sampling functions and obtaining their mean to compare it with the theory’s.
Figure 13 shows simulation of two sampling functions and their mean up to state 7. It should be noted that the mean is, in fact, in the middle of both realizations. Continuing in this way, Figure 14 shows five realizations, considering the seven damage states.
Figure 15 shows 1000 sampling functions simulated and their mean in black. In addition, time expected was obtained with Equation (19), shown in red. It was observed that the difference between the mean obtained from realizations and the one obtained from data decreases as the number of simulations increases, because of this it can be said that the method is consistent. Figure 16 shows the comparison of the time mean in each state using (19) and the Monte Carlo model using 1000 sampling functions and considering the 80 damage states. Figure 16
![]()
Figure 12. Evolution of ![]() calculated in function of λ (modeled).
calculated in function of λ (modeled).
![]()
Figure 13. Two sampling functions simulated with Monte Carlo and its mean, considering the seven damage states measured.
![]()
Figure 14. Five sampling functions simulated with Monte Carlo and its mean, considering the seven damage states measured.
shows that the mean lines are virtually the same, so it can be said that simulations and the theory give similar results. In this way, time in which the mean of the sample function reaches b may be obtained, in this case![]() , that is, time to failure expected. In this way, for instance, to reach state 20, mean time expected is
, that is, time to failure expected. In this way, for instance, to reach state 20, mean time expected is ![]() time steps, and to reach failure
time steps, and to reach failure ![]() time steps.
time steps.
![]()
Figure 15. Comparison of ![]() (red) with the mean of a model of M (black) using 1000 sampling functions (blue) considering the seven damage states measured.
(red) with the mean of a model of M (black) using 1000 sampling functions (blue) considering the seven damage states measured.
![]()
Figure 16. Comparison of ![]() (red) with the mean of a Monte Carlo model (black) using 1000 sampling functions (blue) considering the 80 damage states measured.
(red) with the mean of a Monte Carlo model (black) using 1000 sampling functions (blue) considering the 80 damage states measured.
Until now, the time steps to failure of the pipeline are known. It should be noted that throughout calculation and analysis, time steps ![]() have been considered; however, it should also be considered that each time step used until now has an equivalence in actual time.
have been considered; however, it should also be considered that each time step used until now has an equivalence in actual time.
It should be remembered that x = 7 was considered to realize equations![]() ; however, this number of states was arbitrary and may vary in accordance with certain considerations, depending on each data set. Therefore, it is better to obtain it directly from data. The mean and its state are calculated. Then, the time value expected to that state is also calculated. The mean of this data set is 0.3767 and is in the third state. Upon calculating the state of the mean on the vertical axis of Figure 15 is and projecting it on the horizontal axis, it is found that time elapsed to reach that state is x = 12.5. Relating actual time of four years, in which the inspection was carried out with theoretical time x = 12.5, it is obtained that a time step is equivalent to 0.32 years of actual time. With this data, it is possible to know the actual time to failure. In accordance with the analysis, the mean theoretical time to failure is
; however, this number of states was arbitrary and may vary in accordance with certain considerations, depending on each data set. Therefore, it is better to obtain it directly from data. The mean and its state are calculated. Then, the time value expected to that state is also calculated. The mean of this data set is 0.3767 and is in the third state. Upon calculating the state of the mean on the vertical axis of Figure 15 is and projecting it on the horizontal axis, it is found that time elapsed to reach that state is x = 12.5. Relating actual time of four years, in which the inspection was carried out with theoretical time x = 12.5, it is obtained that a time step is equivalent to 0.32 years of actual time. With this data, it is possible to know the actual time to failure. In accordance with the analysis, the mean theoretical time to failure is ![]() time steps, and in actual time it is
time steps, and in actual time it is ![]() years. In this manner, it is possible to know the mean time to failure of any pipeline having an inspection report, using Markov chains theory.
years. In this manner, it is possible to know the mean time to failure of any pipeline having an inspection report, using Markov chains theory.
4. Conclusions
The spread of corrosion shown in Figure 2 represents the expected evolution of pitting corrosion in the pipe. Note that, in its first stage, the corrosion rate is low; it then increases, before becoming constant until failure. Its explanation is due to there being an average of time that it stays in each state, and since the system starts from there being no damage at the beginning; it can be said that the nucleation time is implicit. Nucleation is the time at which the corrosion cavity begins to form on a microscopic level. In light of the fact that it is an average and it is assumed that the system starts without damage; it takes some time for all of the cavities to be generated. After, there is another stage in which it remains constant. This is because once the cavities have been generated and the film formed, the corrosion rate remains constant, ref. [10].
According to the phenomenon of localized corrosion—as described in the literature, ref. [2] —the behaviour of the corrosion rate is due to the fact that, at an early stage, the part of the metal attacked is completely exposed to a high concentration of corrosive species, while later, a layer of oxides is formed with passive properties between the metal and the corrosive environment, thus serving as a protective barrier against corrosion, ref. [8]. This shows that the corrosion process in a pipe is almost stable if there are no sudden or radical changes that affect the kinetic process, ref. [7].
The model presented here, represents the evolution in time of damage caused by internal corrosion pitting in a hydrocarbon transport pipeline. It allows us to know, in detail, the spread of the corrosion depth at different moments from the time from the data of an inspection report. It is also possible to obtain a transition matrix from a single inspection report, as well as the fact that adjusting the data to a normal log probability distribution avoided numerical problems. That said, it is essential to perform a Kolmogorov-Smirnov test at a 1% level of significance, indicating whether the normal Log distribution can be used with an acceptable level of reliability.
The comparison of the time used in each damage state, according to the theory of accumulated damage and with the Monte Carlo simulations, provides similar values, so it can be affirmed that the model is consistent.
With the model presented it is possible to calculate the expected time to the failure of any pipe that has an inspection report. This can be very useful for the industry to schedule inspections and maintenance.
Acknowledgements
This article and its corresponding research were carried out thanks to the resources of the research projects IPN SIP-20120585. The collaboration of the Flores Méndez and Cortes Yah is appreciated, and the authors thank the reviewers for carefully reading the paper and for their constructive comments and suggestions which have improved the paper.