1. Introduction
The fluid flows over stretching sheet have gained considerable attention in fields of engineering due to its extensive use, such as bundle wrapping, hot rolling, extrusion of sheet material, glass fiber, wire rolling and extrusion of polymer sheet [1]. The fluid behaviour and various physical aspects are associated with the stretching sheet having been discussed by different authors [1] [2] [3] [4]. Recently, the boundary layer flow of nanofluid over a stretching sheet has become very interesting topic among researchers. The steady boundary layer flow, nanoparticle volume fraction and heat transfer in nanofluid over a linear stretching surface were analysed by khan and pop [5]. The nano boundary layer flow over a stretching sheet by applying differential transform method (DTM) was studied by Rashidi and Erfani [6]. Numerical solution of nanofluid flow in permeable rotating sheet was studied by Sheikholeslami and Ganji [7].
Due to peculiar properties, nanofluids are significant in numerous applications in heat transfer including microelectronics, hybrid powered engines, fuel cells, and pharmaceutical processes [8]. Nanofluid, containing nanoparticles was introduced by Choi et al. [9] and discussed the fluid which contains nanoparticles that were suspended in basic fluid, such as ethylne glycol, propylen glycol, water etc. Nanoparticle having high thermal conductive metals, such as, copper, aluminum, silicon or silver helps to intensify the thermal conductivity of such mixtures, which consequently improves over all the energy transport capability. Nadeem and Lee [10] introduced the nanofluid flow over an exponentially stretching sheet. Rana and Bhargave [11] extended the work, and studied the laminar boundary layer flow of a nanofluid over stretching sheet. The effects of magnetic field on a nanofluid over a stretching sheet have been investigated by Sheikholeslami and Chamkha [12]. Model of stagnation point flow of nanofluid over a stretching sheet was developed by Ul Haq et al. [13]. Mixed convection boundary layer fluid flow along a stretching sheet in porous medium was numerically discussed by Mukhopadhayay Som et al. [14].
The study of magnetic effects of nanofluid flow has gained vast attention of engineering and sciences because of its extensive significant industrial applications such as metallurgical process and polymer industry [15]. Sheikholeslami et al. [16] numerically discussed the magnetic field effect on natural convection heat transfer of water-cu and water-cuo nanofluid. Yadav et al. examined the magnetic field effect on sunset of nanofluid convection [17]. Xuan et al. [18] studied the effect of magnetic field on heat transfer of nanofluid flowing through a microchannel. Rashid [19] has been numerically studied the magnetic field effect on steady laminar flow over vertical plate. Ashorynejad et al. [15] have examined the magnetic field effect on natural convection of water-Ag nanofluid between two coaxial circular cavities. Ghasemi et al. [20] numerically investigated study on natural convection heat transfer in an inclined enclosure filled with a water-Cuo nanofluid. Mahumoudi et al. [21] numerically discussed magnetic field effect on the natural convection of water-Cuo nanofluid in triangular enclosure. Hamad [22] had investigated analytical solution of the magnetic field effect on natural convection of nanofluid over stretching sheet. Sheikholeslami and Rashid have study ferrofluid heat transfer in the existence of magnetic field [23]. Sheikholeslami and Ellahi have analyzed the effect of magnetic field on natural convection flow of nanofluid [24].
Alumina (Al2O3) is one of the advance and extensively used ceramic materials. Alumina is one of representative for electrical insulating materials. It has high chemical stability, high thermal conductivity and higher temperature as compared to other electro insulating such as plastic, paper and glass [25] [26] [27]. Al2O3 nanoparticles are plentifully produced and have used in several consumers, domestic, medical, and industrial products [28] [29]. Al2O3 nanoparticles have several military applications [30] due to high combustion enthalpy and pyrotechnic properties, Al2O3 nanoparticles have utilized as fuel in propellents [30] [31] [32]. Al2O3 nanoparticles also used to manufacture the batteries and electrical components [33]. Al2O3 nanoparticles have been proposed to use as a carrier system to enhance drug solubility [34]. Various researchers have been discussed the thermal conductivity ofwater-Al2O3 nanofluid. Numerical study of water-Al2O3 nanofluid between two parallel plates was conducted by Esfe et al. [35].
The shape of nanoparticles is very significant to change thermal conductivity of nanofluid. The present research focuses on to investigate the impacts of nanoparticle shape on Al2O3-water nanofluid and heat transfer over a non-linear radically stretching sheet in the presence of magnetic field and thermal radiation. There are five shapes of nanoparticles which are under consideration; column, sphere, hexahedron, tetrahedron and lamina. Numerical solutions of nonlinear ordinary differential equations (ODE’s) are solved by bvp4c program. The effects of empirical shape factor, solid volume fraction, magnetic field and radiation parameter are discussed in detail.
2. Mathematical Model
We have considered two dimensional, steady and laminar boundary layer flow in water-based nanofluid, having various shapes of Al2O3 nanoparticles, pass over a non-linear radically stretching sheet with influences of magnetic field and thermal radiation. The under contemplated shapes of nanoparticles are column, sphere, hexahedron, tetrahedron and lamina. The radically stretching sheet is placed at z = 0, transverse magnetic field and radiation field are applied along the z-axis, which are shown in Figure 1. Furthermore, a cylindrical co-ordinate system (r, θ, z) has been used. The flow is in rotational symmetry, so the physical quantities are independent of θ. The components of velocities u and w are direction of r and z respectively. The partial governing equations of the axisymmetric flow are
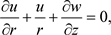 (1)
(1)
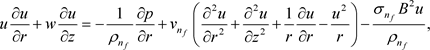 (2)
(2)
![]()
Figure 1. Schematic model and co-ordinate system.
 (3)
(3)
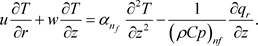 (4)
(4)
The nanofluid flow is happened due to stretching sheet, there is no role of pressure gradient in the fluid flow field. The above equation after applying the boundary layer approximation has reduced as shown in [37].
 (5)
(5)
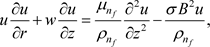 (6)
(6)
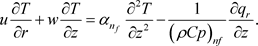 (7)
(7)
With the boundary conditions related to problem are given by
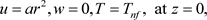
 (8)
(8)
here a > 0 is stretching constant. The effective features of nanofluids are
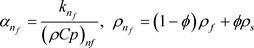
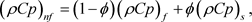 (9)
(9)
Here  and
and 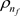 are represented the density of base fluid, solid and nanofluid respectively.
are represented the density of base fluid, solid and nanofluid respectively. 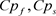 and
and 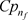 have represented the specific heat of base fluid, solid and nanofluid respectively.
have represented the specific heat of base fluid, solid and nanofluid respectively.  is represented the solid volume fraction.
is represented the solid volume fraction. ![]() is the thermal diffusivity of nanofluid.
is the thermal diffusivity of nanofluid. ![]() is the thermal conductivity of nanofluid.
is the thermal conductivity of nanofluid.
Hamilton and crosser [38] have been presented a model for solid-liquid mixture to account the effect of particles shape. When thermal conductivity of the nanoparticles become 100 greater than base fluid![]() , The Hamilton and crosser model are expressed as following as:-
, The Hamilton and crosser model are expressed as following as:-
![]() (10)
(10)
where
represents the thermal conductivity of solid. The ![]() represents the thermal conductivity of base fluid. The m represents the shape factor and its numerical values are given in Table 1. Furthermore, thermophysical properties of liquid and solid nanoparticles are presented in Table 2.
represents the thermal conductivity of base fluid. The m represents the shape factor and its numerical values are given in Table 1. Furthermore, thermophysical properties of liquid and solid nanoparticles are presented in Table 2.
By using the nonlinear Rosseland approximation, the radiation flux converted into form
![]() (11)
(11)
That the temperature within the flow, such as that ![]() may be expressed as a temperature liner function. Hence by expanding
may be expressed as a temperature liner function. Hence by expanding ![]() by Taylor series and neglecting higher order terms, we obtained the following relation
by Taylor series and neglecting higher order terms, we obtained the following relation
![]() (12)
(12)
By Employing Equations (11) and (12), Equation (7) converted into
![]() (13)
(13)
The similarity transformation of Equations (5)-(9) and stokes stream function ![]() are defined in the following form
are defined in the following form
![]()
Table 1. Values of the empirical shape and the sphericity of nanoparticle as [36]
![]()
Table 2. Thermophysical properties of Al2O3 and pure water.
![]()
![]() (14)
(14)
Here ![]() and
and ![]() are the dimensionless stream function and similarity variable respectively. Re is the local Reynolds number, it defined as
are the dimensionless stream function and similarity variable respectively. Re is the local Reynolds number, it defined as![]() . Moreover
. Moreover ![]() is the quadratic stretching velocity. Thus the velocity components are
is the quadratic stretching velocity. Thus the velocity components are
![]() and
and ![]() (15)
(15)
By the Equation (15) into Equations ((5)-(6)) and Equation (13), the Equation (5) identical satisfied Equation ((6), (13)) and their related boundary value conditions reduce as
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
where![]() .
.
Here M is the Magnetic parameter, it is defined as![]() .
. ![]() is the Radiation parameter, it is defined as
is the Radiation parameter, it is defined as![]() . Moreover, Pr is the Prandlt number, it is defined as
. Moreover, Pr is the Prandlt number, it is defined as![]() .
.
The quantity of particle interest in this problem is the Nusselt number defined as
![]() (19)
(19)
where ![]() is the wall heat flux given by
is the wall heat flux given by
![]()
Using Equation (6) into Equation (13), we get
![]() (20)
(20)
3. Result and Discussion
To get clear heat transfer rate for each shape of nanoparticles, numerical values with pertinent parameters have shown in the form of graphs. From Figures 2-8, it has distinguished that heat transfer rate is decreasing function of solid volume fraction, magnetic and radiation parameters. The lamina shape of nanoparticles, with![]() , M = 1.0, and Rd = 1.0 have played remarkable in rate of heat transfer, while performance of sphere shape of nanoparticles in term of heat transfer is lowest than the other shape of nanoparticles. It is distinguished that
, M = 1.0, and Rd = 1.0 have played remarkable in rate of heat transfer, while performance of sphere shape of nanoparticles in term of heat transfer is lowest than the other shape of nanoparticles. It is distinguished that
![]()
Figure 2. Various shapes (a)-(e) of the Al2O3 nanoparticles as from reference [36].
![]()
Figure 3. The effect of ![]() on Nusselt number for
on Nusselt number for![]() .
.
![]()
Figure 4. The effect of M on Nusselt number![]() .
.
![]()
Figure 5. The effect of ![]() on Nusselt number for
on Nusselt number for![]() .
.
performance of heat transfer in nanoparticles is such as Lamina > Column > Tetrahedron > Hexahedron > Sphere.
The graphical depictions are used to illustrate the relation of appropriate parameters on velocity profiles and thermal boundary layers. The solid volume fraction is very significant parameter for nanofluid. Figure 9 illustrates that the
![]()
Figure 6. The effect of ![]() on Nusselt number for
on Nusselt number for![]() .
.
![]()
Figure 7. The effect of M on Nusselt number for![]() .
.
velocity profile is an increasing function of solid volume fraction. It is also distinguished from Figure 10 that the velocity of nanoparticles decreases with increase in the magnetic field. The reason is that the resistance force, which has produced by magnetic field, opposes the flow and reduces the fluid motion. Figure 11 reveals the effects of nanoparticles’ shapes on dimensionless temperature with same basic fluid and other parameters, and it has observed that the lamina > column > tetrahedron > hexahedron > sphere. It has also been noted that lamina shape nanoparticles have maximum temperature due to minimum viscosity and thermal conductivity whereas sphere shape nanoparticles have minimum temperature due to its maximum viscosity.
![]()
Figure 8.The effect of ![]() on Nusselt number for
on Nusselt number for![]() .
.
![]()
Figure 9. The effect
of ![]() on velocity profile of nanoparticles for
on velocity profile of nanoparticles for![]() .
.
![]()
Figure 10. The effect of M on velocity of nanoparticles for![]() .
.
Figure 12 shows variation of solid volume fraction in temperature profile for different shapes of nanoparticles. The shape nanoparticles are increasing function of solid volume fraction. Deduction; nanoparticles contribute to increasing thermal conductivity of base fluid; consequently, heat is transferred from radical sheet to the fluid with rapidly and has heated the thermal boundary region. Thus as the convergence of nanoparticles in base fluid raised, the temperature in the thermal boundary layer has also been raised. The thermal boundary layer thickness due to effect of solid volume fractionin lamina shapes nanoparticles is more energetic. The effect of magnetic field on nanoparticles’ shapes has been plotted in Figure 13. The lamina shape nanoparticles seem animated on other shapes of nanoparticles. Usually in boundary layer flow, the radiation parameter produces additional heat. Figure 14 depicts the variation of thermal radiation on thermal
boundary layer thickness of nanoparticles. It is noted that the temperature raised with intensifying value of radiation parameter, because in the presences of thermal radiation implies an immense enlarging in the radiative heat which encourage thermal state of nanofluid initiate temperature to intensify. Thermal boundary layer thickness of lamina shape nanoparticles observed more animated by thermal radiation effect.
4. Conclusions
The shapes effect of nanoparticles effects on boundary layer flow and heat transfer in Al2O3-water nanofluid over a non-linear radically stretching sheet have been designed in this study. The effects of nanoparticles shape, solid volume fraction, magnetic field and thermal radiation on thermal boundary layer and heat transfer rate with value of prandtle number (Pr = 6.2) have discussed in details. Non-linear thermal radiation is taken into consideration. The following results have been proven:
· The lamina shape of nanoparticles acts as principle in lead of disturbance on thermal boundary layer thickness.
· The tetrahedron shape of nanoparticles acts amidst role in disturbance of thermal boundary layer thickness.
· The sphere shape of nanoparticles shows lowest role in disturbance of thermal boundary layer thickness.
· The lamina shape of nanoparticles shows remarkable role in the rate of heat transfer.
· Performance of tetrahedron in form of heat transfer is amidst.
· Performance of sphere shape of nanoparticles in the form of heat transfer is lower than other nanoparticles shapes.
Heat transfer properties are considerably dependent on the shape effect of nanoparticles. Herein, possible increment of characteristic of water while seeded with nanoparticles is worthwhile in terms of shape effect. These considerations should be taken into account for future research directions regarding technical advancement of nanofluidics, micro mixing and energy conversion to have economically viable operations.