Semiconductor Fluorinated Carbon Nanotube as a Low Voltage Current Amplifier Acoustic Device ()
1. Introduction
Drift, diffusive and tunnelling current flow are the dominant carrier transport mechanisms in semiconductor structures [1] [2]. Ballistic carrier motion is witnessed in some cases, provided that the size of the sample is smaller than the electron mean-free path in some pure novel nanostructures. Conceptually different from these mechanisms are transport phenomena based on momentum and energy exchange from an externally propagating entity to the electron medium [1] [2]. Fundamentally, the propagation of sound wave through a piezoelectric material sets up an electric field due to the periodically strained regions. Conduction electrons response to this effect, leads to a spatial redistribution of the carriers. Electrons bunch up at the minima of potential energy which is periodic due to the sound wave. As a result of the difference in velocities between the electrons and the acoustic wave, there is a phase difference between the electric field and the wave. This causes a momentum transfer from the sound wave to the electrons that leads to an attenuation of the acoustic wave [3]. For most of the conduction electrons, this component of velocity will be much larger in magnitude than the speed of the acoustic wave, so that these electrons are “out of phase” in relation to the propagating electric field, thus creating the so-called acoustoelectric effect (AE) [4] [5] [6].
Other interesting effects are observed during the process of energy and momentum exchange. These effects occur not only during the scattering of quasi-momentum carriers by lattice vibrations, but also occur when acoustic waves are propagating through these structures. Among the mechanisms witnessed include: absorption (amplification) of acoustic phonons [7] [8] [9] [10] [11], acoustomagnetoelectric effect [12], acoustothermal effect [13] and acoustomagnetothermal effect [13]. Recently, AE was studied in semiconductor fluorinated carbon nanotube (FSWCNT) with double periodic band in the absence of an external electric field [14].
Modification of single-walled carbon nanotubes (SWCNT) with fluorine dopants is one of the emerging and efficient processes for chemical activation and functionalization of carbon nanotubes [15] [16]. Fluorination of multi-walled carbon nanotubes (MWCNT) was performed decades ago, which was followed by single-walled nanotube in the latter years [17] [18]. Fluorination plays a significant role in the functionalization process, as it provides a high surface concentration of functional groups, up to C2F without destruction of the tube’s physical structure. Functionalization is an easy, fast exothermic reaction, and the repulsive interactions of the fluorine atoms on the surface debundles the nanotube, thus enhancing their electron dispersion [19] [20] [21] [22] [23]. Despite all these studies, no research has been reported on FSWCNT with double periodic band, as a low voltage, current amplifier acoustic device in the hypersound regime. Therefore, the objective of this manuscript is to study AE in FSWCNT as a function of the electric field, electron-phonon interaction, electron concentration, temperature and the acoustic wavenumber by employing a tractable analytical approach. For increasing wavenumber, electron concentration and electron-phonon interaction, the acoustoelectric current increases in magnitude is positive and but reverses direction depending on the field (+ve or −ve). Increasing temperature also decreases the net acoustoelectric current which also is positive but reverses direction from positive to negative. We believe that different behaviours observed at positive and negative fields, corresponding to different acoustic wavelengths, reflect the different length scales over which the acoustic waves probe the electronic properties of the FSWCNT semiconductor in the presence of external electric field.
2. Theory
Fluorination plays a significant role in the doping process, as it provides a high surface concentration of functional groups, up to C2F without destruction of the tube’s physical structure. Doping is an easy, fast, exothermic reaction. The repulsive interactions of the fluorine atoms on the surface debundles the nanotube, thus enhancing their electron dispersion. Consider a fluorine modified SWCNT (n, n) with the fluorine atoms forming a one-dimensional chain. A nanotube of this nature is equivalent to a band with unit cell as shown in Figure 1, where b is the bond length (c-c). The width for the F-(n, n) tube equals n periods (with a periodic length of 3b), and this unit cell contains
carbon atoms and the atomic numbering in the unit cell of the FSWCNT (n, n) nanotube are shown in Figure 2. For a conjugated π-system in which there is alternation of single and double bonds along a linear chain, the Hückel matrix approximation is employed to determine the electronic energy band. The dispersion relation for the fluorine doped single walled carbon nanotube (FSWCNT) where the fluorine atoms form a one-dimensional chain is deduced in [24] as:
(1)
where
,
is a constant, N is an integer. Choosing
, the energy dispersion for FSWCNT at the edges of the Fermi surface is expressed as:
(2)
![]()
Figure 1. Fluorinated nanotube FSWCNT (n, n) (dots denotes the positions of fluorine atoms that are covalently bonded to C atoms) [24].
![]()
Figure 2. Atom numbering in the unit cells of nanotubes FSWCNT (n, n) [24].
Expanding Equation (2) yields:
(3)
where
,
, and
is the overlapping integral for jump.
is the minimum electron energy in the first Brillouin zone with momentum
, i.e.
.
Following the model developed in refs. [2] [4] [10] [14] and employing a tractable analytical approach, we assume that the sound flux and the external electric field are along the FSWCNT axis (z-axis). The AE current density can then be written as:
(4)
where
is the solution to the Boltzmann kinetic equation in the absence of a magnetic field, and the kinetic equation is given as:
(5)
is the electron momentum along the axial direction of the FSWCNT and
in Equation (4) is the electron-phonon interaction term expressed as:
(6)
here
is the unperturbed electron distribution function,
is the sound flux density,
is the sound velocity in the medium,
is the energy band, n and n’ denotes the quantization of the energy band, and
is the matrix element of the electron-phonon interaction. Denoting
and substituting into Equation (6) and employing the principle of detailed balance, we obtain:
(7)
The matrix element of the electron-phonon interaction is given as:
(8)
where K is the piezoelectric modulus,
is the lattice dielectric constant,
is the density of FSWCNT and the net AE current density is given as:
(9)
where
is the electron mean free path defined as:
(10)
and
(11)
Substituting Equation (10) and Equation (11) into Equation (9) yields
(12)
The electron distribution function in the presence of the applied electric field,
is obtained by solving the Boltzmann transport equation in the τ-approximation. That is
(13)
which has a solution of the form
(14)
and
is the Fermi-Dirac distribution given as
(15)
where
is the quasi Fermi-level which ensures the conservation of electrons, k is the Boltzmann’s constant, T is the absolute temperature in energy units. Substituting Equation (14) and Equation (15) into Equation (10), we obtain an equation for
as:
(16)
which contains the Fermi-Dirac integral (
) of the order 1/2 as
(17)
where
. For nondegenerate electron gas, where the Fermi level is several kT below the conduction band edge
, (i.e.
), the integral in Equation (17) approaches
. The unperturbed distribution function can be expressed as:
(18)
where
is the normalization constant to be determined from the normalization condition
as:
(19)
here
is the electron concentration, and
is the modified bessel function of zero order. Assume the electrons are confined to the lowest mini-band, then
. The velocity of the system is also given as:
(20)
Making use of the transformation
(21)
and substituting Equation (14)-(20) into Equation (12), with a little bit of algebra, we obtain the AE current density as:
(22)
where
Simplifying Equation (22) yields
(23)
where
is the acoustoelectric current density in the absence of an external electric and is given in [14] as:
(24)
and
3. Results and Discussion
The AE current density obtained in Equation (23) shows a strong nonlinear dependence on the acoustic wavenumber (q), frequency (
) temperature (T) and the dimensionless electric field (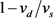 ). Equation (23) is analyzed numerically with the following parameters:
). Equation (23) is analyzed numerically with the following parameters: ,
, 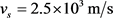 ,
, 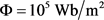 ,
, 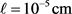 and
and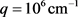 .
.
Equation (23) can be solved explicitly under two conditions: 1) in the absence of an electric field when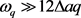 ,
, 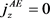 , there is no absorption of acoustic waves and thus no AE current present. The FSWCNT under such a condition can be used as a current filter and this phenomenon has been observed in [14]. 2) In the presence of a weak field
, there is no absorption of acoustic waves and thus no AE current present. The FSWCNT under such a condition can be used as a current filter and this phenomenon has been observed in [14]. 2) In the presence of a weak field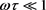 , we obtain Equation (23) which shows a strong nonlinear dependence of
, we obtain Equation (23) which shows a strong nonlinear dependence of 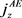 on (
on ( ).
).
The AE current density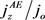 , rises to a maximum, and falls off in a manner similar to that observed in negative differential conductivity (NDC) [4] [21] - [26] as shown Figure 3, when
, rises to a maximum, and falls off in a manner similar to that observed in negative differential conductivity (NDC) [4] [21] - [26] as shown Figure 3, when  [2] [3] [4]. Conversely, when
[2] [3] [4]. Conversely, when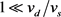 ,
, 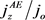 decreases to a minimum value and starts to rise (see Figure 3) [2] [3] [4]. In the presence of weak scattering
decreases to a minimum value and starts to rise (see Figure 3) [2] [3] [4]. In the presence of weak scattering , the electron gains energy in the vicinity of the electric field and streams upwards until it reaches the top of the band where Bloch waves reaches the boundary of the brillouin zone. The electron reflects back and continues its propagation in the opposite direction, decelerating until it reaches the bottom of the band (Bragg’s reflection) [25] - [30]. The nonlinear dependence of
, the electron gains energy in the vicinity of the electric field and streams upwards until it reaches the top of the band where Bloch waves reaches the boundary of the brillouin zone. The electron reflects back and continues its propagation in the opposite direction, decelerating until it reaches the bottom of the band (Bragg’s reflection) [25] - [30]. The nonlinear dependence of ![]() on
on ![]() for varying q values is shown in Figure 3. It is observed that as q increases, the peak of
for varying q values is shown in Figure 3. It is observed that as q increases, the peak of ![]() increases to a maximum before falling to its minimum value. The reason being that, there are more acoustic phonons to trade their energies and momenta to the intra-mini-band electrons to generate a high AE current [11]. Per numerical analysis, when
increases to a maximum before falling to its minimum value. The reason being that, there are more acoustic phonons to trade their energies and momenta to the intra-mini-band electrons to generate a high AE current [11]. Per numerical analysis, when![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() ,
,![]() . The corresponding minimum currents are:
. The corresponding minimum currents are:![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() ,
,![]() . The negative
. The negative ![]() observed when
observed when ![]() is due to the intra-mini-band electrons reversing direction and moving opposite to the field which is attributed to strong hypersound flux with an increasing electric field.
is due to the intra-mini-band electrons reversing direction and moving opposite to the field which is attributed to strong hypersound flux with an increasing electric field.
The dependence of ![]() on
on ![]() for varying T is shown in Figure 4. It can be inferred that, there is a decrease in the peak values of
for varying T is shown in Figure 4. It can be inferred that, there is a decrease in the peak values of![]() , as the temperature increases. Numerically, for
, as the temperature increases. Numerically, for![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() ,
,![]() . The corresponding minimum current densities occur at: for
. The corresponding minimum current densities occur at: for![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() ,
,![]() . This is because increasing temperature increases the scattering process in the FSWCNT. The majority of electrons in this case acquire a higher velocity, and attains a higher kinetic energy. These energetic electrons which are the majority carriers undergo inter-mini-band transition allowing only a handful to undergo intra-mini-band transition. Thus, these few intra-mini-band electrons interact with the co-propagating acoustic phonons leading to a decrease in the AE current,
. This is because increasing temperature increases the scattering process in the FSWCNT. The majority of electrons in this case acquire a higher velocity, and attains a higher kinetic energy. These energetic electrons which are the majority carriers undergo inter-mini-band transition allowing only a handful to undergo intra-mini-band transition. Thus, these few intra-mini-band electrons interact with the co-propagating acoustic phonons leading to a decrease in the AE current,![]() . The I-V characteristic curve for the varying temperatures intersects at different
. The I-V characteristic curve for the varying temperatures intersects at different ![]() values indicating that at these points of intersections they have the same q values.
values indicating that at these points of intersections they have the same q values.
The AE current as shown in Figure 5, is seen to be highly sensitive to the electron concentration ![]() and works better for moderate
and works better for moderate ![]() within 1016 - 1019 cm−3 without introducing strong electron-electron interactions. Higher
within 1016 - 1019 cm−3 without introducing strong electron-electron interactions. Higher ![]() increases the reverse current without screening out the piezoelectric field to lower the AE current density. Again, increasing the electron concentration increases the AE current, because more intra-mini-band electrons are interacting with the acoustic phonon to generate current densities. This means the electron concentration can be used to tune the FSWCNT to obtain a higher AE current at room temperature and may hold potential for current amplifying acoustic material for ultrasound current source density imaging (UCSDI) and AE hydrophone devices [31].
increases the reverse current without screening out the piezoelectric field to lower the AE current density. Again, increasing the electron concentration increases the AE current, because more intra-mini-band electrons are interacting with the acoustic phonon to generate current densities. This means the electron concentration can be used to tune the FSWCNT to obtain a higher AE current at room temperature and may hold potential for current amplifying acoustic material for ultrasound current source density imaging (UCSDI) and AE hydrophone devices [31].
However, in Figure 6 we observe a strong nonlinear dependence of ![]() on
on ![]() for different values of electron-phonon interactions,
for different values of electron-phonon interactions,![]() . Increasing
. Increasing![]() , increases the reverse AE current significantly to about 2.5 times the forward current. This implies that there are more intra-mini-band electrons which interact strongly with the co-propagating acoustic phonons to generate the high AE current in the reverse direction. The strong nonparabolicity of the dispersion relation in FSWCNT is also assumed to be a contributory factor to the observed bahaviour.
, increases the reverse AE current significantly to about 2.5 times the forward current. This implies that there are more intra-mini-band electrons which interact strongly with the co-propagating acoustic phonons to generate the high AE current in the reverse direction. The strong nonparabolicity of the dispersion relation in FSWCNT is also assumed to be a contributory factor to the observed bahaviour.
![]()
Figure 3. The nonlinear dependence of ![]() on
on ![]() for varying wavenumber (q).
for varying wavenumber (q).
![]()
Figure 4. The dependence of ![]() on
on ![]() for varying temperature T.
for varying temperature T.
4. Conclusion
AE was studied in a non-degenerate FSWCNT semiconductor using a tractable analytical approach in the hypersound regime![]() . In the presence of an external electric field, a strong nonlinear dependence of
. In the presence of an external electric field, a strong nonlinear dependence of ![]() on
on ![]() which strongly depends on
which strongly depends on![]() , q and T was observed. The AE current obtained is highly nonlinear and depends on the attenuation of acoustic phonons by electric field driven electrons experiencing intra-mini-band transition. However, the electron concentration can be used to tune the AE current of the FSWCNT (see Figure 5) which will offer the potential for room temperature application as an acoustic switch or transistor and also as a material for ultrasound current source density imaging (UCSDI) and AE hydrophone devices in biomedical engineering. Moreover, our results prove the feasibility of implementing chip-scale non-reciprocal acoustic devices in an FSWCNT platform through acoustoelectric amplification.
, q and T was observed. The AE current obtained is highly nonlinear and depends on the attenuation of acoustic phonons by electric field driven electrons experiencing intra-mini-band transition. However, the electron concentration can be used to tune the AE current of the FSWCNT (see Figure 5) which will offer the potential for room temperature application as an acoustic switch or transistor and also as a material for ultrasound current source density imaging (UCSDI) and AE hydrophone devices in biomedical engineering. Moreover, our results prove the feasibility of implementing chip-scale non-reciprocal acoustic devices in an FSWCNT platform through acoustoelectric amplification.
Nomenclature