Quadrature Rules for Functions with a Mid-Point Logarithmic Singularity in the Boundary Element Method Based on the x = tp Substitution ()
1. Introduction
In this paper the problem of determining an efficient quadrature rule for and integral of the form
(1)
in which
is a continuously differentiable function, except for having weak logarithmic singularity at its mid-point (when
), is considered. A weak logarithmic singularity is one in which the behaviour near the singularity is of the form
. In this work, we look at finding near-optimal quadrature rules for the numerical evaluation of this class of integral. In the outcome, it is noted that the method proposed method may be generalised and applied to stronger singularities.
Integrals like the one above typically occur in implementation of the two-dimensional (2D) boundary element method (BEM) [1] [2] [3] , when the observation point lies at the parametric mid-point of the element or panel. The governing partial differential equation is reformulated as a boundary integral equation, and the latter is solved in order to determine unknown boundary properties. The boundary is represented by a set of panels, with functional representations of the properties on those panels that ascribe the boundary elements. By applying a suitable integral equation method, such as collocation, the boundary integral equation is resolved into a linear system of equations, with each row of the matrices representing a geometrical line integral of each panel with respect to a particular boundary observation (e.g. collocation) point.
In the boundary element method, the integrals are generally found numerically, although in a number of special cases the integrals can by evaluated analytically [4] . For two-dimensional problems, the logarithmic singularity occurs when the observation point lies on the panel over which the integration is applied. For constant elements, where the functional representation of boundary properties is a constant value on each panel, the diagonal components of the matrices correspond to singular integrals. All of the other integrals are regular and are therefore amenable to standard quadrature methods, often Gauss-Legendre quadrature rules for their optimal efficiency. However, some panels are close to the observation point, and the corresponding integral are regular, but are also strongly-varying, and some researchers also apply special treatment to these nearly-singular integrals [5] .
Much of the aforementioned story is the same for three-dimensional problems, except that, in this case, the bounding surface is represented by a mesh, made up
of panels. However, in 3D we have
like singularities (where r represents
the distance between the observation point and the point on the panel). There have been a number of papers addressing the problem of integrating functions like this for general 3D problems in the BEM, both numerically [6] and analytically [7] , although this is outside the scope of this paper. However, for the particular class of axisymmetric 3D problems, the first azimuthal integration over the panel results again in a logarithmic
singularity in the remaining integral along the generator of the panel and for these problems this work is applicable.
In the previous work on the boundary element method by the first author [8] - [13] , typical elements that are applicable include straight-line panels for 2D problems in which the boundary function approximated by a constant, with the observation points located at the centres of the panel. Similarly, axisymmetric problems are modelled by constant elements and the panels are equivalent to conic sections. Typical panels for approximating the boundary in 2D and axisymmetric 3D are illustrated in Figure 1, with the node at the (parametric) centre of the straight-line panel and at the centre of the generator on a truncated conical panel. Hence a 2D panel or the generator of a 3D axisymmetric panel can be mapped onto the domain [−1, 1], with the mid-point of the panel mapping to zero. Although the problem posed in this paper is restrictive in that the singularity is defined to be at the parametric centre of the panel, this is also the most common case in practice, and this is all that is required for these simple elements.
The principles underlying the method choice include the usual one of efficiency; that of accuracy in relation to the number of quadrature points or function evaluations. However, the other principle is that the method must be a practical method as it must be typically included into the BEM as an “automatic computation” of the singular integrals that arise therein. In this paper, the numerical integration method is developed through a simple power substitution focussed at the singularity. This sort of transformation is similar to the technique of transforming the integrand by a polynomial substitution in Telles [14], except the problem considered therein is more general in the sense that the singularity may be located anywhere within the domain (−1, 1) and the substitution was with a general cubic. The concept is also similar to the method of the first author [8] - [13] , except in that work the domain of the integration was [0, 1] with the singularity at zero and the method was applied on either side of the mid-point, as a composite integral, and summed in order to determine the integral. However, in general, composite integrals are less efficient.
In this paper, integration through the substitution
with p taking odd integer values and Gauss-Legendre quadrature applied to the resulting integral. This method of transformation is preferred because of its effectiveness and mathematical and computational simplicity. The selection of the value of p is explored by applying the method to test problems. The objective is to obtain guidance on the value of p that returns a quadrature formula that is close to optimal for the numerical integration of the singular functions occurring typically in the BEM.
This paper is organised as follows. In Section 2, the logarithmic integrals are placed in the context of the boundary element method, where they typically arise. Various methods of treating singular integrals are considered in Section 3, with a particular focus on the
substitution. In Section 4 methods based on the
substitution are applied to test problems and results are summarised and conclusions are given in Section 5.
![]()
Figure 1. A straight-line panel (2D) and a truncated conical panel (3D).
2. The Boundary Element Method and Singular Integration
The motivation for exploring the numerical evaluation of singular integrals in this work is in that they arise in the boundary element method. The BEM is a computational technique that has developed from the reformulation of elliptic partial differential equations as boundary integral equations. The method is the computational result of solving the partial differential equations via the discretisation of the boundary integral equations.
In principal, the boundary element method has the significant advantage over “domain methods”—such as the finite element method and the finite difference method—in that it only requires an elemental decomposition of the boundary, rather than the full domain. Hence, when the boundary element method is applicable, it typically requires significantly fewer elements than the corresponding domain methods, there is less to mesh and there is a potential reduction in computation time. However, the boundary element method is not without its challenges, and not the least of these is the evaluation of singular integrals. Although singular integrals of the same form occur in all application areas of the BEM, in order to motivate the need for such methods and to study their place within the BEM, in this paper the two related partial differential equations studied by the authors are considered; the exterior Laplace and Helmholtz equations [3] [8] - [13] .
2.1. Typical Boundary Integral Equations (Exterior Helmholtz and Laplace Problems)
The example of a partial differential equation that can be solved by the boundary element method is the exterior Helmholtz (reduced wave (acoustic)) equation:
(2)
where E is a domain exterior to a closed boundary S,
is the potential and k is the wavenumber. The domain is illustrated in Figure 2.
For example, the elementary direct formulation of the Helmholtz equation can be reformulated as the following integral equation:
(3)
where
represents an appropriate Green’s function with
(4)
in two dimensions and
(5)
in three dimensions, with
,
,
and
is the unit outward normal to the boundary.
is the Hankel function of the first kind of
order zero . The “
” in Equation (3) is only true if the boundary S is smooth at
![]()
Figure 2. An illustration of a boundary S and the exterior domain E.
, as it is in the boundary element method discussed here, in which
takes the values of the centre of the straight-line panels in 2D or on the centre of the generator of the axisymmetric panels in 3D, as illustrated in Figure 1.
Laplace’s equation is the special case of the Helmholtz Equation (2) with
, which can be reformulated as the boundary integral Equation (3), with the Green’s function
replaced by
. The Green’s function for Laplace’s equation are defined as
(6)
in two dimensions and
(7)
in three dimensions. The Green’s functions determine the form of the weak singularity, as discussed earlier in this paper.
2.2. Boundary Element Method and Singular Integrals
The boundary element method is derived from the boundary integral equation by approximating and representing the boundary S as a set of n panels
and the boundary functions
and
are approximated
using characteristic functions on each panel, defining the elements. The most straightforward integral equation method to apply is that of collocation. When this is applied to the collocation point
, the discrete analogue of the boundary integral Equation (3), is as follows:
(8)
where
and
.
Forming the above equation for all collocation points returns a system of n simultaneous linear equations that is written as a linear system of equations in matrix-vector form
(9)
where
,
,
and
, where
and
are matrices that are the discrete equivalent of
the integral operators in (8). The vectors
and
list the values of
and v at the collocation points, either predetermined by the boundary condition or an approximation to the same following the solution of the system (9).
2.3. Practical Aspects of the BEM
The components of the matrices
and
are normally determined by numerical integration. The integrands that make up the components of the
matrix are regular functions. The integrands that make up all but the diagonal components of the
matrix are also regular. However, the integrands corresponding to the diagonal components of the
matrix have a
singularity in 2D and
singularity in 3D at the corresponding collocation point. Hence the number of integrations typically required in the boundary element method is
, where n is the number of elements, whereas the number of singular integrals is
. This is an important factor in the design of the boundary element method; efficient and accurate evaluation of the singular integrals is important, but the burden is unlikely to be significant in terms of the overall computational cost of the boundary element method. There are also codes that parallelise the numerical integration method [15] , which could also reduce the computer time required to calculate the BEM matrices.
It is well known that elementary boundary element methods for the solution on the exterior Helmholtz equation are unreliable for some values of k, dependent on the domain and nature of the boundary condition [16] . Robust integral equation formulations have been derived, not least the Burton and Miller formulation [17] , based on a combination of the boundary integral Equation (7) and an its derivative. Unfortunately, this also introduces hypersingular integrals that also require special treatment [18] . Similarly, if the boundary element method is applied to thin structures then this also introduces the same hypersingular operator [19] [20] [21] . For the simple flat straight line and triangular panels used in the first author’s previous work, simple formulae were developed for the analytic integration of singular and hypersingular operators [11] [12] . However, it is the treatment of the weakly singular integrals that correspond to the diagonal components of the
(or
) matrix in the boundary element system (9) that are considered in the main in this paper.
The singular integrals corresponding to the
(or
) operator, with the singularity at the paramtric centre in 2D can be transformed onto [−1, 1] and they are then of the form (1). In axisymmetric 3D, the integrations are first carried out in the azimuthal direction, leaving a singularity in the integral along the generator, at the parametric centre, and this can also be transformed on to a problem of the form (1).
3. Treatment of the Singular Integrals
In this section, the various methods for evaluating the singular integrals are reviewed. Let us first consider the position of the singularity. In this work, we have placed the singularity at the centre of the domain, in this case the standard interval [−1, 1]. In other contributions [22] the same domain is used but the singularities are placed at both ends and Gauss-Jacobi rules are applied. In the previous work of the first author [8] - [13] the domain [0, 1] is used and the singularity is placed at zero. The work of Telles [14] generalises the concept in allowing the singularity to be anywhere within the domain.
In variable integration, wherever the singularity is, it is only typically integrable if it is of logarithmic type or of algebraic type with an index greater than −1. For example, in the case of the interval adopted in this work [−1, 1] with the singularity at the centre, typical integrable singularities are of the logarithmic type
or algebraic type
where
. The logarithmic type of singularity is weaker than the algebraic type and hence, although the topic of this work is the treatment of logarithmic singularities, methods that have been developed for integrating algebraic singularities can also be applied in the context of logarithmic singularities.
3.1. Ignoring the Singularity
Given the general effectiveness in numerical integration methods such as Gaussian quadrature, the singularities are generally of the weakest form and the fact that the computation time for computing the integrals is unlikely to be a critical factor in the boundary element method lends weight to the argument that the singularity should be ignored.
The technique of ignoring the singularity in numerical integration has been the subject of research [23] [24] . In Kirkup [8] [9] it is shown that the integration of
with 8, 16 and 32 point Gaussian quadrature rules gives quadrature errors of 8.8 (−3) (8.8 × 10-3), 2.3 (−3) and 6.0 (−4) respectively; doubling the number of quadrature points reduces the error by a factor of four. For the original problem (1) it is found that applying the Gaussian quadrature straightforwardly gives an error of 4.9 (−1) for the 4-point rule, 2.5 (−1) for the 8-point rule, 1.7 (−1) for the 12-point rule and 1.3 (−1) for the 16-point rule; very poor convergence.
It can reasonably be concluded that ignoring the singularity is a technique that is worthy of consideration in the context of the boundary element method. However, it should be expected that a rule with a high number of quadrature points would be required to maintain reasonable accuracy. If the singularity is within—rather than at the extremities of—the domain of integration, then splitting the domain at the singularity and applying a composite rule would also seem to be necessary. This approach would have a marginal impact on computer processing time in the BEM, but it would lack finesse.
3.2. Product Integration
If the singularities can be characterised by another function, e.g.
, where the singularity is located at
, then a product integration method is appropriate, in which the characteristic singularity
is effectively absorbed into the quadrature rule. For example, Gaussian-Jacobi quadrature rules are available and are applicable when there is an algebraic singularity at the extremes of the range of integration [22] . Anderson [25] derives quadrature formulas with a weighting function of
on [0, 1].
Test Problem
By differentiating
, the integrand in the integral below is obtained (for
)
(10a)
and noting that the function has an
singularity at
.
This gives a useful test problem in the domain [0, 1]
(10b)
Reflecting the integrand from the positive to the negative domain give as test problem on the original domain
 (10c)
(10c)
which also includes the 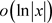 singularity, specified in the original problem (1). Applying the eight-point Gauss rule with the
singularity, specified in the original problem (1). Applying the eight-point Gauss rule with the  weighting in [25] gives a relative error of 3%. Ideally, for the test problem (1) a product integration rule
weighting in [25] gives a relative error of 3%. Ideally, for the test problem (1) a product integration rule
for  could be a useful way forward. In order to use the same
could be a useful way forward. In order to use the same
points for the other operators, the integrands could be divided by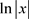 .
.
3.3. Subtracting out the Singularity
“Subtracting out” the singularity is a popular method of treating the singular integrals in the boundary element method. The technique simply involves splitting the integrand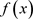 , so that it is the sum of two functions, one that is singular and one that is regular. For example, let
, so that it is the sum of two functions, one that is singular and one that is regular. For example, let 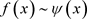 near to the singularity; writing
near to the singularity; writing 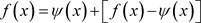 and the latter integral may be regular [26] .
and the latter integral may be regular [26] .
Clearly this in itself does not entirely solve the problem since one singular integral has been replaced by another. However, there are two reasons for subtracting out the singularity. The first is that 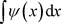 could be evaluated once-and-for-all and then re-used with different
could be evaluated once-and-for-all and then re-used with different  functions. The second reason is that it is sometimes possible to find an analytic expression for
functions. The second reason is that it is sometimes possible to find an analytic expression for . In such cases the methods for treating singular functions considered in this section may need to be applied to evaluate
. In such cases the methods for treating singular functions considered in this section may need to be applied to evaluate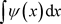 .
.
Subtracting out the singularity with test problem (10b)
The method of subtracting out a singularity that can be evaluated analytically can be illustrated on the test problem (10b):

where the final “1” is obtained by integrating the subtracted-out function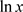 . Applying an eight-point Gaussian quadrature to the regular integral above gives less than 1 × 10-12 % error. Similarly, for the integral with the singularity at the centre (10c), the subtraction gives the following regular integral:
. Applying an eight-point Gaussian quadrature to the regular integral above gives less than 1 × 10-12 % error. Similarly, for the integral with the singularity at the centre (10c), the subtraction gives the following regular integral:
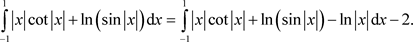
In this case the application of an 8-point Gaussian quadrature rule returns an error of 5 × 10−10%. A graph of the original integrand for the test function and the integrand with the singularity subtracted out is shown in Figure 3, indicating that the remaining function is regular.
Returning to original form of the test problem (1), the typical boundary element integrals (8), the integrands are functions of distance from the collocation point. A good example of this is with the Helmholtz operators considered earlier; if the discrete Laplace operators are computed once-and-for all, then this subtracted out value could be use on the corresponding Helmholtz problems for each chosen value of k. For example, in (9), the singularity is subtracted out as follows:

For example there are analytic expressions for ![]() in the case
in the case
of straight-line or planar triangular panels [11] [12] . For the two-dimensional problem,
![]()
where ![]() and
and ![]() are Bessel functions. The Bessel functions are real-valued and hence the equation above gives the subtracted-out function in real and imaginary parts. The graphs in Figure 4 for
are Bessel functions. The Bessel functions are real-valued and hence the equation above gives the subtracted-out function in real and imaginary parts. The graphs in Figure 4 for![]() , assuming the panel lies on
, assuming the panel lies on
[−1, 1] and the collocation point is at the centre. The graphs indicate that—once the singularity is subtracted out—the functions are regular.
Subtracting out the singularity in the BEM for the axisymmetric Helmholtz Equation
Two examples of axisymmetric problems are considered in order to observe the nature of the remaining function on the generator, once the Green’s function
for the 3D Helmholtz equation (![]() ) is integrated over azimuthal angles
) is integrated over azimuthal angles
using the H3ALC code [3] [11] [12] , with ![]() and with
and with ![]() subtracted out. In Figure 5(a) the panel is parallel to the axis and in Figure 5(b) the panel is at right angles to the axis, and in both cases the remaining function is apparently regular.
subtracted out. In Figure 5(a) the panel is parallel to the axis and in Figure 5(b) the panel is at right angles to the axis, and in both cases the remaining function is apparently regular.
3.4. Substitution or Transformation
The main purpose of this paper is to develop techniques based on power substitution, as initiated in the Introduction. Generally, the main purpose of the substitution is to transform the integrand from being a singular function to a regular
![]() (a)
(a)![]() (b)
(b)
Figure 5. (a) Generator function for [1, 0] - [1, 1]: real part, imaginary part. (b) Generator function for [0, 0] - [1, 0]: real part, imaginary part.
function, which is then amenable to standard quadrature. In this section the context of using substitution ahead of applying quadrature is reviewed.
The fundamental basis of this method is substituting one function for x. In
general let ![]() and hence
and hence![]() , and hence with suitable changes of limits we may write
, and hence with suitable changes of limits we may write
![]()
with the rationale that the transformed integrand is more suited to standard quadrature. In this section we consider methods based on the transformation of the integral.
Erf rule
The erf rule is based on the substituting the error function (erf) for x, with any possible singularities corresponding to the argument of the error function being either ±∞ and hence it is applicable to an end-point rather than a mid-point singularity. The method was put forward in the area of the boundary element solution of acoustic/Helmholtz problems by Burton [27] . Consider the problem
![]()
with the singularity remaining at![]() . The substitution
. The substitution![]() , transforms the singularity to −∞ where erfc is the complement of the error function. As
, transforms the singularity to −∞ where erfc is the complement of the error function. As ![]() it follows that
it follows that
![]()
The integrand is now regular and because of the fast decay of the Gaussian the integrand is only significant in a narrow interval of t, the integration range can be severely truncated in practice. This, alongside the finding that functions with a Gaussian envelope have been found to be approximates very accurately by the trapezium rule [28] results in the erf rule being an efficient method for integrating singular functions [29] [30] . For example with the test problem (10b) the erf rule with integration points at t = −3, −2.5, −2, −1.5, −1, −0.5, 0, 0.5, 1, 1.5, 2, 2.5, and 3 (13 points) has a relative error of 1.1 (−4).
Polynomial Transformation
Most simply, a polynomial transformation is achieved by a substitution or power transformation of the form
![]() (11)
(11)
gives the following
![]() (12)
(12)
in which the location of the former logarithmic singularity is now at![]() , but for a large enough value for p (and for a logarithmic singularity this is for
, but for a large enough value for p (and for a logarithmic singularity this is for![]() ) the new integrand is continuous. However, the lower limit is only practical if p is also an odd integer, so that the lower limit is −1, and in this case the domain of integration is usefully unchanged by the transformation, as shown in Equation (13):
) the new integrand is continuous. However, the lower limit is only practical if p is also an odd integer, so that the lower limit is −1, and in this case the domain of integration is usefully unchanged by the transformation, as shown in Equation (13):
![]() (p is an odd integer,
(p is an odd integer,![]() ). (13)
). (13)
The concept of transforming the integral so that both a regular integrand was returned and the domain was unchanged is developed in Telles [14] , in which a cubic polynomial, rather than a simple power substitution, is applied. In the first author’s previous work the weak singularities in three-dimensional axisymmetric case are handled by the splitting the integral at the singularity and applying the transformation![]() on the [0, 1] domain and applied either side of the singularity [8] [9] [11] [12] .
on the [0, 1] domain and applied either side of the singularity [8] [9] [11] [12] .
Notes
The transformations of the integral outlined are the ones that are most often used in the boundary element method. Clearly there are a range of substitutions that can be applied for the same purpose. If the singularity is within the domain then the methods based on the erf rule requires the interval to be split at the singularity and a method to be applied either side. This was also the case with the power method in some cases, such as the ![]() substitution discussed earlier. If the domain needs to be split then this means that a composite quadrature is effectively being applied, and this is often going to be less efficient than a quadrature rule designed for the full domain. Telles [14] suggests the substitution of a cubic and maintaining the same domain of [−1, 1] following transformation. If the singularity is in the centre of the domain, as in the objective problem in this paper, then this is achieved by simplifying the method in Telles to
substitution discussed earlier. If the domain needs to be split then this means that a composite quadrature is effectively being applied, and this is often going to be less efficient than a quadrature rule designed for the full domain. Telles [14] suggests the substitution of a cubic and maintaining the same domain of [−1, 1] following transformation. If the singularity is in the centre of the domain, as in the objective problem in this paper, then this is achieved by simplifying the method in Telles to![]() .
.
4. Results for x = tp
In this section numerical integration methods that arise through the power substitution ![]() in the integral (1) with Gauss-Legendre quadrature rules applied to the transformed integral. These methods are employed to find approximations to the integrals of the test problems of
in the integral (1) with Gauss-Legendre quadrature rules applied to the transformed integral. These methods are employed to find approximations to the integrals of the test problems of ![]() and
and ![]() . Both test problems have an
. Both test problems have an ![]() singularity in the centre of the domain of integration [−1, 1]. All Gauss-Legendre rules were generated using the Keisan on-line calculator [31] .
singularity in the centre of the domain of integration [−1, 1]. All Gauss-Legendre rules were generated using the Keisan on-line calculator [31] .
Gaussian quadrature rules with an even number of points avoid having a point at the centre of the domain (where the singularity is located) and so standard 8, 12 and 16 point Gauss-Legendre rules and a range of odd values of p are applied in the first case. Given that the transformed integrand is zero at the centre (for![]() ) the central point can be ignored and hence 5-, 9-, 13- and 17-point rules can be applied as 4-, 8-, 12- and 16-point rules. A spectrum of results are obtained, from which decisions about the choice of the near-optimal value of the power p may be explored.
) the central point can be ignored and hence 5-, 9-, 13- and 17-point rules can be applied as 4-, 8-, 12- and 16-point rules. A spectrum of results are obtained, from which decisions about the choice of the near-optimal value of the power p may be explored.
Let the Gauss-Legendre with m points be defined on [−1, 1] and have weights ![]() and abscissae
and abscissae ![]() for
for![]() . Transforming the integral through the substitution
. Transforming the integral through the substitution ![]() (13) and applying the Gauss-Legendre quadrature rule to the transformed integral returns the following method of approximation:
(13) and applying the Gauss-Legendre quadrature rule to the transformed integral returns the following method of approximation:
![]()
The quadrature rule is now in the standard form with weights ![]() and
and![]() .
.
4.1. Gauss-Legendre Rules with an Even Number of Points
The results from applying the method to the test problems are listed in Table 1 and Table 2 for various values of p and for 4-, 8-, 12- and 16-point Gaussian Legendre rules applied to the resulting integral. The smallest error for each Gaussian rule with the various p-values is given in bold, indicating the optimum value for p.
4.2. Discussion
The most important point to be taken from the results in the tables above is that the optimal power substitution is significantly larger than those that have been used previously (i.e. p = 2 or 3, as discussed). The optimal value of p increases significantly with the number of Gauss points for the ![]() test problem, but much more steadily for the more-realistic test problem in Table 2. In Table 1 the p = 1 is equivalent to ignoring the singularity, as discussed in Subsection 3.1.
test problem, but much more steadily for the more-realistic test problem in Table 2. In Table 1 the p = 1 is equivalent to ignoring the singularity, as discussed in Subsection 3.1.
The Gauss-Legendre points ![]() for
for ![]() are spread fairly evenly on [−1, 1]. The effect of the power transformation is to cluster the quadrature points
are spread fairly evenly on [−1, 1]. The effect of the power transformation is to cluster the quadrature points ![]() closer to the singularity at zero as p becomes larger and the weights
closer to the singularity at zero as p becomes larger and the weights ![]() corresponding to the clustering points are correspondingly smaller with proximity to the singularity. For example, for one of the methods that performs well is the 16-point rule with p = 9 and the data associated with this method is shown in Table 3.
corresponding to the clustering points are correspondingly smaller with proximity to the singularity. For example, for one of the methods that performs well is the 16-point rule with p = 9 and the data associated with this method is shown in Table 3.
As the weights associated with the points close to the singularity are “small” then a further adjustment to the method is to delete these points since they contribute very little to the integral and they require function evaluations. This is particularly effective when the power substitution p is large. For example, simply
![]()
Table 1. Numerical error in ![]() following
following ![]() substitution and Gauss rule.
substitution and Gauss rule.
![]()
Table 2. Numerical error in ![]() following
following ![]() substitution and even Gauss rule.
substitution and even Gauss rule.
deleting the two points closest to the singularity returns an error of 2.8 (−6), compared to the error of 2.4 (−6) when the points are included; a marginal loss of accuracy. In order that the weights sum to 2 the weights for deleted points may be added with the ones nearest to them: in this case the error is 2.6 (−6).
4.3. Gauss-Legendre Rules with an Odd Number of Points
Following on from the discussion in the previous Subsection and the introduction to this Section, if the quadrature rule has a point in the centre of the domain then for weighting is zero for ![]() and that point can be deleted. In Table 4, 5-, 9-, 13- and 17-point Gauss-Legendre rules are applied, deleting the mid-point so that the actual numbers of points are 4, 8, 12 and 16.
and that point can be deleted. In Table 4, 5-, 9-, 13- and 17-point Gauss-Legendre rules are applied, deleting the mid-point so that the actual numbers of points are 4, 8, 12 and 16.
4.4. Test Problem
In order to demonstrate the improvements in efficiency through using the rules
![]()
Table 4. Numerical error in ![]() following
following ![]() substitution and odd Gauss rule.
substitution and odd Gauss rule.
a test problem is set up comparing the power transformation with ![]() with those suggested by the results in Table 4. The test problem is that of calculating
with those suggested by the results in Table 4. The test problem is that of calculating
![]() for an axisymmetric three-dimensional problem (
for an axisymmetric three-dimensional problem (![]() , where
, where![]() ). The panel
). The panel ![]() is generated by (r, z) end-point coordinates
is generated by (r, z) end-point coordinates
(0, 1) and (1, 1). The point ![]() is at the centre of the generator, the location of the singularity. The results with the optimal values of power p are compared with
is at the centre of the generator, the location of the singularity. The results with the optimal values of power p are compared with![]() , in Table 5.
, in Table 5.
5. Conclusions
The handling of singular integrals is a continual area of enquiry in the implementation of the boundary element method. This paper explores this again, but for integrating over panels in two-dimensional and axisymmetric three-dimensional problems and with the singularity lying at the parametric centre of the panel in 2D and of the generator in axisymmetric 3D. The issue of singular integration in the boundary element method is therefore considered in one of the simplest forms; with a logarithmic singularity (![]() ) for 2D problems, or when the integral is resolved onto the generator in axisymmetric 3D. Hence the subject of this paper; the numerical integration of functions with a mid-point logarithmic singularity is one of the most typical problems within the boundary element method.
) for 2D problems, or when the integral is resolved onto the generator in axisymmetric 3D. Hence the subject of this paper; the numerical integration of functions with a mid-point logarithmic singularity is one of the most typical problems within the boundary element method.
The boundary element method is considered in the context of its solution of Laplace’s equation and the Helmholtz equation. It was discussed that within the BEM, generally there are ![]() regular integrals and
regular integrals and ![]() singular integrals and so in that context the computational cost of the evaluating singular integrals is unlikely to have a significant impact on the running time of the BEM. However, it is still useful to have practical, robust and reasonably efficient methods for evaluating the singular integrals [32] [33] [34] .
singular integrals and so in that context the computational cost of the evaluating singular integrals is unlikely to have a significant impact on the running time of the BEM. However, it is still useful to have practical, robust and reasonably efficient methods for evaluating the singular integrals [32] [33] [34] .
The boundary element method normally requires the evaluation of the discrete form of a number of integral operators, of which at most one will have the logarithmic singularity of this enquiry. However, the integrands in all required integral operators that occur are functions of r, the distance of the integration
point from the singularity, and hence there is significant merit (in terms of computational cost) in using the same quadrature rule for all the integral operators that are required. Pursuing the optimal integration method for one integral operator, as we are in this work, without reference to the other integral operators will not necessarily return the best overall integration rule for the BEM. In practice, the aim is to achieve a numerical integration method that works well for all required operators in the boundary element method.
Various methods for handling singularities are discussed in Section 3. “Subtracting out” the singularity is a generally useful method, for example with solving the Helmholtz Equation (2) for a range of values for the wavenumber, the subtracted out integral may be evaluated “once and for all” and then used for each value of k. For the cases of 2D and axisymmetric 3D problems, once the singularity is subtracted out, the remaining integral is regular. However, “subtracting out” the singularity does not completely avoid the issue of singular integrals.
An appropriate substitution can transform a singular integral into a regular one. The two main substitutions that have been employed in the BEM were outlined in Section 3; the erf rule or a polynomial or power substitution. The polynomial or power substitution is generally attractive because of its relative simplicity. For the problem considered in this paper (1), with the singularity at the centre, the power transformation ![]() (with
(with ![]() and an odd number) is a simple method for regularising the integral, and usefully maintains the same domain of integration; standard quadrature rules can be applied directly.
and an odd number) is a simple method for regularising the integral, and usefully maintains the same domain of integration; standard quadrature rules can be applied directly.
The results from applying the ![]() substitution, followed by Gaussian quadrature, are given in Section 4. Gauss-Legendre rules are applied with an even number of points, so that evaluation at the centre could be avoided. In Table 1 and Table 2 the numerical error resulting from applying 4, 8, 12 and 16-point Gauss-Legendre rules to the transformed test integrals are tabulated for a range of values of the power p. It is noted that as p increased the transformed quadrature points clustered closer to the singularity, with smaller transformed weighting, and an example of this is given in Table 3. Hence there is a potential for deleting the transformed quadrature points that are very close to the singularity with a marginal loss of accuracy and a shortened processing time. Table 4 shows
substitution, followed by Gaussian quadrature, are given in Section 4. Gauss-Legendre rules are applied with an even number of points, so that evaluation at the centre could be avoided. In Table 1 and Table 2 the numerical error resulting from applying 4, 8, 12 and 16-point Gauss-Legendre rules to the transformed test integrals are tabulated for a range of values of the power p. It is noted that as p increased the transformed quadrature points clustered closer to the singularity, with smaller transformed weighting, and an example of this is given in Table 3. Hence there is a potential for deleting the transformed quadrature points that are very close to the singularity with a marginal loss of accuracy and a shortened processing time. Table 4 shows
![]()
Table 6. Near-optimal quadrature rules for functions with a mid-point logarithmic singularity.
the results of the ![]() substitution followed by a Gauss Legendre rule with an odd number of points with the central point deleted (with no effect on accuracy). The results in Table 4 generally compare favourably with the results in Table 2, the corresponding results requiring the same processing time.
substitution followed by a Gauss Legendre rule with an odd number of points with the central point deleted (with no effect on accuracy). The results in Table 4 generally compare favourably with the results in Table 2, the corresponding results requiring the same processing time.
A notable conclusion from this work is in the guidance it suggests for the optimal value for p. From the results of the more realistic test problem in Table 2 and Table 4, the optimal values of p are 5 or 7 for the 4-point rules, p = 7 for the 8 or 12-point rules and p = 9 for the 16-point rule. The extent of the transformation of the integral runs with the power p, but the effects of this are offset by the improved continuity properties.
The near-optimal quadrature rules for integrating functions with a logarithmic mid-point singularity, based on this method and the test results are given in Table 6. The resulting “optimal” methods have been applied to a test problem of integrating over an axisymmetric panel with a 1/r singularity, typically found in the boundary element method.
In this paper the solution of integrals on [−1, 1] with a midpoint logarithmic singularity have been explored, with a particular focus on the ![]() transformation followed by Gauss-Legendre quadrature, where p is an odd number and
transformation followed by Gauss-Legendre quadrature, where p is an odd number and![]() . Based on the results, the recommendation is to choose a high value of p of 5 or 7 for quadrature rules with few points and use larger values of p as the number of points increases, as indicated in the results. Standard quadrature rules with a point at the centre (e.g. Gauss-Legendre rules with an odd number of points) are useful, as the central point may be deleted. The results are compared with the
. Based on the results, the recommendation is to choose a high value of p of 5 or 7 for quadrature rules with few points and use larger values of p as the number of points increases, as indicated in the results. Standard quadrature rules with a point at the centre (e.g. Gauss-Legendre rules with an odd number of points) are useful, as the central point may be deleted. The results are compared with the ![]() substitution in Table 4 and Table 5, the outcome of Telles work, and the superior convergence and significant improvements in accuracy are evident.
substitution in Table 4 and Table 5, the outcome of Telles work, and the superior convergence and significant improvements in accuracy are evident.