Periodic Solution for Stochastic Predator-Prey Systems with Nonlinear Harvesting and Impulses ()
1. Introduction
It is well known that the dynamic relationship between predator and prey has always been one of the main topics in ecology and mathematical ecology. In the past decades, many predator-prey models have been proposed and widely used to describe the food supply relationship between two species [1] [2]. At the same time, it has attracted great attention in many different fields, such as bio-economics. Recently, the interaction of predator-prey with harvesting has been studied. The effect of harvest on population is beneficial to sustainable development and renewable resource management, so many scholars take harvest into account in their models. The capture intensity depends largely on the capture strategy being implemented. Common harvest functions are: constant harvest, proportional harvest and nonlinear harvest. Gupta et al. proposed a predator-prey model with nonlinear predator in harvest [3] and discussed the dynamical properties of the following system:
(1.1)
On the other hand, the growth of species in nature is often limited by environmental factors. Generally speaking, there are two main types of environmental noise: white noise and colored noise. Wenjie Zuo et al. [4] considered the white noise and studied the stationary distribution and periodic solution. However, reading the literature found that studies on the non-linear harvesting of predators and prey are very few literatures [5] [6] [7]. Therefore, the following model is proposed.
(1.2)
In real life, however, ecosystems are often disturbed by human development or by activities related to natural factors such as drought, floods, earthquakes, and planting. In order to describe this phenomenon more accurately, impulses perturbation is added into the model. To sum up, this paper mainly studies the effects of impulse effect and nonlinear harvesting on predator and prey populations, and proposes the following interesting stochastic system.
(1.3)
where
and
represent the density of prey and predator populations respectively. The parameters
are positive, and
is the internal growth rate of prey, and
is the mortality rate of predator.
and
represent the intra-specific competition coefficients of prey and predator populations, respectively. The coefficient
is the predator’s capture rate and
stands for the rate at which nutrients are converted to predators. In addition,
are the nonlinear harvesting.
Throughout this paper, unless otherwise specified, we suppose
be a complete probability space with a filtration
satisfying the usual conditions and it is right continuous and increasing, while
contains all
-null set. All the coefficients are assumed to be T-periodic continuous functions.
The remainder of this paper is organized as follows. In Section 2, we show that the model (1.3) existence of the global positive solution. In Section 3, sufficient conditions are achieved to guarantee the existence of a positive periodic solution of the stochastic system (1.3) by using Itô’s formula. In Section 4, we discuss the globally attractive of stochastic model (1.3). In Section 5, we use numerical simulation to illustrate our results.
2. Existence and Uniqueness of Global Positive Solution
First, to facilitate the analysis that follows, we make the following tags. When
is a continuous T-periodic function, we define:
Moreover, we assume that a product equals unity if the number of factors is zero.
Definition 2.1. [8] Consider an impulsive stochastic differential equation
(2.1)
A stochastic process
is said to be a solution of ISDE (2.1), if
satisfies
1) x(t) is
adapted and is continuous on
and each interval
and
;
2) x(t) obeys the equivalent integral equation of (2.1) for almost every
and satisfies the impulsive conditions at each
;
3) For each
,
and
exist and
with probability one.
We give the main results of system (1.3) as follows.
Theorem 2.1. For any initial value
the system (1.3) has a unique global positive solution
for
and the solution remains in
with probability one.
Proof. First, we construct the following SDE without impulses:
(2.2)
with the initial value
, where
,
Then it is obvious that
,
are positive T-periodic functions. In fact,
(2.3)
For any
, there is an integer n, such that
.
The limited mathematical induction procedures, together with
,
induce that
(2.4)
According to
, there exists
such that
(2.5)
Thus, combining (2.2)-(2.4), we obtain
Similarly,
.
By the same method as [9] and standard proof [10], Equation (2.2) has a unique global positive Solution
.
Next we will show that
is the solution of system (2.2), which is continuous on each interval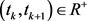 . For any
. For any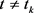 .
.
Let
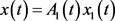 ,
,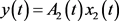 .
.
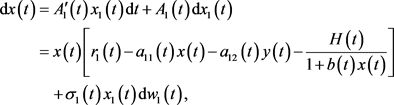
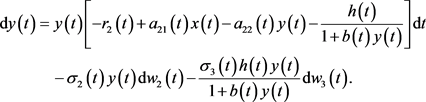
And, for every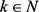 ,
,
 ,
,
 .
.
Similarly, we can show that,
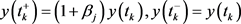 .
.
Therefore, 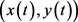 is a solution that satisfies system (1.3) Finally, we prove the nonnegative uniqueness of the solution of system (1.3) (more details see [11]).
is a solution that satisfies system (1.3) Finally, we prove the nonnegative uniqueness of the solution of system (1.3) (more details see [11]).
Then the proof is completed.
3. Existence of Periodic Solutions of the System
In this section, we give the existence of the positive periodic solution of the stochastic system (1.3) with impulses. For convenience of readers, we first give the definition of the periodic solution of the impulsive stochastic differential equation in the sense of distribution and the results of the existence of periodic solutions (see [10] [11]).
Definition 3.1. [12] A stochastic process 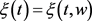 is said to be periodic with period T, if for every finite sequence of numbers
is said to be periodic with period T, if for every finite sequence of numbers 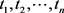 the joint distribution of random variables
the joint distribution of random variables  is independent of h, where
is independent of h, where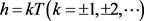 .
.
Consider the following periodic stochastic differential equation without impulse:
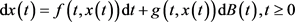 (3.1)
(3.1)
where 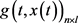 is a
is a 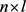 matrix function,
matrix function, ![]() and the matrix
and the matrix ![]() are T-periodic in t.
are T-periodic in t.
Lemma 3.1. [12] [13] Assume that the system (3.1) has a global solution, and there exists a T-periodic function ![]() such that the following conditions hold:
such that the following conditions hold:
1) ![]() on the outside of some compact set;
on the outside of some compact set;
2) ![]() , as
, as![]() .
.
Then Equation (3.1) has a T-periodic solution.
According to Lemma 3.2, we can obtain the main result in this section.
Theorem 3.1. Assume
(H1): ![]()
(H2):![]() ,
,
(H3):![]() ,
,
(H4):![]() .
.
Then system (1.4) has a positive T-periodic solution.
Proof. We only need to prove the existence of a periodic solution of the equivalent system (2.2) without impulses. The global existence of the solution has been ensured by Theorem 1. Then, we only have to verify the conditions of by Lemma 3.1.
Define a C2-function![]() :
:
![]() (3.2)
(3.2)
where ![]() will be determined later. Here,
will be determined later. Here, ![]() satisfies
satisfies
![]() (3.3)
(3.3)
![]() (3.4)
(3.4)
Which ![]() and
and ![]() are defined by (H1), (H2). Obviously,
are defined by (H1), (H2). Obviously, ![]() are T-periodic functions. And
are T-periodic functions. And ![]() is a bounded function. Thus there is
is a bounded function. Thus there is ![]() such that;
such that;
![]() ,
,![]() (3.5)
(3.5)
In order to confirm the condition (2) of Lemma 3.1, we only need to prove that
![]() , as
, as![]() .
.
where![]() , here the coefficients of the quadratic term
, here the coefficients of the quadratic term ![]() of
of ![]() are all positive.
are all positive.
Next, we verify the condition (1) of Lemma 3.2. By Itô’s formula, we have:
![]()
![]()
![]()
As ![]() so that:
so that:
![]()
Let![]() ,
, ![]() ,
, ![]() , we have
, we have
![]()
![]()
![]()
Then
![]() (3.7)
(3.7)
Then
![]()
where:
![]()
![]()
Let, we take
![]() (3.8)
(3.8)
To confirm the condition (1) of Lemma 3.2, we choose a sufficiently small constant ε such that:
![]() (3.9)
(3.9)
![]() (3.10)
(3.10)
where
![]() (3.11)
(3.11)
Define a bounded open set
![]() .
.
and denote
![]() ,
, ![]() ,
,
![]() ,
,![]() .
.
It is obvious that![]() . Next,
. Next, ![]() on
on ![]() must be shown.
must be shown.
Case 1: If![]() , then
, then![]() , we have:
, we have:
![]()
Using (3.8) and (3.9), we obtain
![]() .
.
Case 2: If![]() , then
, then![]() , we have:
, we have:
![]()
By the definition (3.8) of C and the inequalities (3.9), we have:
![]() .
.
By Young inequality, we have![]() . Then by equality (3.11), the following inequality is obvious:
. Then by equality (3.11), the following inequality is obvious:
![]()
Case 3: If![]() , from (3.9) and (3.10), we obtain
, from (3.9) and (3.10), we obtain
![]() .
.
Case 4: If![]() , from (3.9) and (3.10), we obtain
, from (3.9) and (3.10), we obtain
![]() .
.
Thus, we obtain ![]() on
on![]() , and the condition (1) of Lemma 3.2 is satisfied. Therefore, by Lemma 3.2, system (1.3) has a positive T-periodic solution.
, and the condition (1) of Lemma 3.2 is satisfied. Therefore, by Lemma 3.2, system (1.3) has a positive T-periodic solution.
The proof is confirmed.
4. Globally Attractive
Theorem 4.1. [14] [15] If system (1.3) satisfies![]() ,
, ![]() , then the system (1.3) is globally attractive.
, then the system (1.3) is globally attractive.
Proof. Let![]() ,
, ![]() be two arbitrary solutions of model (1.3) with initial values
be two arbitrary solutions of model (1.3) with initial values![]() .
.
We defined the following Lyapunov function
![]()
Then by calculating the right differential ![]() and employing Ito’s formula.
and employing Ito’s formula.
When![]() , we have:
, we have:
![]()
![]()
![]()
when![]() , we get
, we get
![]()
Integrating both sides and then taking the expectation yields that
![]()
That is
![]()
Then, in the view of ![]() and
and ![]() that
that![]() . Thus, it is easy to see from Lemmas 6.1 [15]
. Thus, it is easy to see from Lemmas 6.1 [15]
![]()
The proof is complete.
5. Computer SimulationsIn
this section, we will prove our theoretical results by some examples with the help of the Matlab software [16] and reveal the influence of impulses and the white noise.
Example 1.
Let
![]()
then
![]()
![]() .Thus, the conditions of Theorem 3.1. hold. Then the model (1.3) has a positive
.Thus, the conditions of Theorem 3.1. hold. Then the model (1.3) has a positive ![]() -periodic solution. Figure 1 confirms the results.
-periodic solution. Figure 1 confirms the results.
Example 2. Set![]() . Making condition of the Theorem 4.1 is satisfied. We get that system (1.3) is globally attractive (see Figure 2).
. Making condition of the Theorem 4.1 is satisfied. We get that system (1.3) is globally attractive (see Figure 2).
![]()
Figure 1. A solution of system (1.4) with the initial value![]() . The left is the phase diagram of the stochastic system, and the right is the phase diagram of the deterministic system.
. The left is the phase diagram of the stochastic system, and the right is the phase diagram of the deterministic system.
![]()
Figure 2. The figure shows the attractiveness of system (1.4), the blue and red lines represent the solution of prey and predator species.
6. Conclusion
In this paper, we propose a stochastic predator-prey system with nonlinear harvesting and impulsive perturbations. Firstly, we show that there is a unique positive solution in system (1.3). Secondly, the system has a positive periodic solution under a certain condition. Result shows that when the impulses are sufficiently large such that ![]() then the predator and prey will tend to exhibit periodicity. It is verified by constructing the appropriate Lyapunov functions and using Itô’s formula. Moreover, these methods used in this study can be extended to more complex and realistic models.
then the predator and prey will tend to exhibit periodicity. It is verified by constructing the appropriate Lyapunov functions and using Itô’s formula. Moreover, these methods used in this study can be extended to more complex and realistic models.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (11861027) and Natural Science Foundation of Guangxi (2016 GXNSFAA380194).