Research of Three-Phase Unbalanced Treatment in Low-Voltage Distribution Network Based on New Commutation Switch ()
1. Introduction
With the development of current society and the increase of people’s electricity consumption, the problem of power quality is becoming more and more obvious. Single-phase load in rural power network is relatively large, and it causes three-phase imbalance. Three-phase unbalance has great harm to power grid, including increasing line loss, power distribution system output reduction and generating zero sequence current [1].
Because of this, many measures have been taken to solve the three-phase unbalance problem. The control technologies of three-phase unbalance mainly use three-phase load automatic regulation devices, including capacitive devices, power electronic devices and commutation switch devices etc. However, the capacitive devices only realize the three-phase load balance of the distribution low-voltage outlet, and unable to solve the problem of actual load balanced distribution fundamentally [2] [3]. The power electronic devices need to use multiple single-phase inverters, make the equipment larger and have high costs. So the commutation switch devices are used more and more widely.
The paper introduces a new type of the commutation system, which uses the two-phase thyristor parallel contactor structure. In terms of algorithm implementation, the objective function and constraint condition are established and IQGA is proposed to solve the problems of QGA in the commutation control strategy. At last, the rationality and the efficiency of the method are verified by a practical example.
2. The Structure of the Commutation System
The traditional commutation switch hardware uses relay and permanent magnet breaker mode, this kind of commutation switch has short mechanical life and long commutation time. In order to solve this problem, the project uses the two-phase thyristor parallel contactor structure, the commutation process has no impact and fast switching speed, the structure diagram is shown in Figure 1.
This kind of commutation switch has three advantages:
Firstly, the commutation switch uses zero-crossing commutation technology and the commutation time does not exceed 10 ms. It can avoid large inrush current at the moment of load switching and avoid affecting users’ electrical equipments.
Secondly, the commutation switch is energy-saving and reliable. By using the two-phase thyristor parallel contactor structure, it can avoid the heating problem caused by long-term operation of semiconductor devices in traditional commutation switches and will greatly improve the stability and safety of the distribution network. The device itself has low loss, and has no electromagnetic and noise pollution to the environment.
Thirdly, the CGMESH network communication is used between commutation switches. The CGMESH network is a Mesh multi-hop network based on IPV6. It
![]()
Figure 1. The structure of commutation switch.
takes CGR as the root node, extends and expands wireless network coverage by the multi-hop mode of multi-stage mutual relay. In the CGMESH wireless Mesh network, wireless nodes can communicate with remote backstage end-to-end direct IPV6, and parallel two-way communication can be carried out between wireless nodes in wireless network.
3. The algorithmic Implementation
3.1. The establishment of Objective Function and Constraint Condition
For the three commutation switches of ABC phase, the amplitude of three-phase current monitored by monitoring and control system is Iai, Ibi, Ici, i = 1, 2, 3, ∙∙∙, n. For n terminal systems, the three-phase current amplitude of the system [4] is
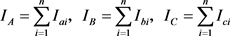 (1)
(1)
The system observes three-phase current by means of timing monitoring, time is set to 10 min, during this period, the monitoring system needs to analyze the monitored three-phase current and judge the threshold. The average value of three-phase current in the system is:
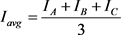 (2)
(2)
The ratio of the difference of three-phase current amplitude to the average value of system current is:
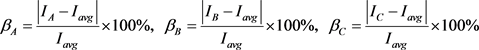 (3)
(3)
In the formula, βA, βB, βC represent the values of the A, B, and C phase imbalances respectively.
Considering that the switching times of intelligent commutation switch installed in actual distribution network are limited, the paper takes the minimum commutation number as one of the objective functions. The model of whether the ith switch commutates is
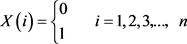 (4)
(4)
If the ith switch does not need to be commutated, X(i) = 0; if the ith switch needs to be commutated, X(i) = 1.
Then the total number of switching commutations can be expressed as
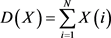 (5)
(5)
Establish objective function with minimum commutation times:
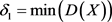 (6)
(6)
In order to suppress the three-phase unbalanced current of the bus-bar, establish the objective function with the lowest three-phase unbalance [5]:
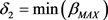 (7)
(7)
Considering the situation of actual distribution network, it is necessary to ensure that the single-phase current does not exceed the maximum carrying capacity of the line after commutation, and the three-phase imbalance must meet the requirements of national standards, so the corresponding constraint condition is established, as shown in formula (8).
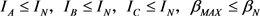 (8)
(8)
In the formula, IN refers to the rated current of the line, βN refers to the required value of the unbalance degree.
3.2. The commutation Control Strategy
3.2.1. Quantum Genetic Algorithm (QGA)
QGA is the product of the combination of quantum computation and genetic algorithm, and it is a hybrid heuristic algorithm, which combines the diversity of quantum evolutionary algorithm with the global optimization ability of genetic algorithm.
In the QGA, chromosomes are no longer represented by traditional binary or floating-point numbers, and they are represented by quantum bits instead. The advantage of this method is that it can express arbitrary superposition states at the same time, that is, a single quantum bit does not represent a definite value, instead, it can represent both 0 and 1 and any superposition between them. The chromosome structure of quantum bits can be expressed as:
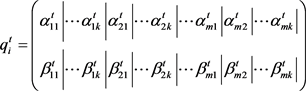 (9)
(9)
In the formula, 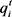 is the chromosome of the i-th individual of the t-th generation in the population; α and β are the quantum probability amplitude, and both of them are complex constants, besides,
is the chromosome of the i-th individual of the t-th generation in the population; α and β are the quantum probability amplitude, and both of them are complex constants, besides,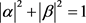 ; is t m he number of genes in the chromosome, and is the decision variable of the optimization function; k is the quantum digits of each gene. As the algorithm progresses, the probability amplitude will change to complete population update, and this is mainly achieved by quantum revolving gates.
; is t m he number of genes in the chromosome, and is the decision variable of the optimization function; k is the quantum digits of each gene. As the algorithm progresses, the probability amplitude will change to complete population update, and this is mainly achieved by quantum revolving gates.
The basic working principle of quantum revolving gate [6] is
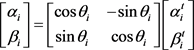 (10)
(10)
In the formula, αi and βi are the probability amplitude of the i-th quantum bit on the t-th generation chromosome updated through the revolving gate; θi is the rotation angle, and its value is pre-set according to algorithm strategy.
Comparing with the traditional genetic algorithm (GA), the probability amplitude representation of quantum bits makes QGA more parallel, the solution speed of the method is accelerated and the diversity of the population is increased at the same time. The population update mode of quantum gate keeps the diversity of population, improves the search efficiency of the algorithm, and makes the algorithm have better convergence property.
3.2.2. Improved Quantum Genetic Algorithm (IQGA)
QGA has gradually replaced traditional GA and has been applied in many engineering fields. But the QGA also has many problems that need to be improved. First, in the evolutionary mechanism, the magnitude and direction of quantum rotation angle are fixed, and this is not conducive to the convergence speed of the algorithm. Second, when the population evolves to a certain degree and the optimal value remains unchanged, there may be premature phenomena in the algorithm. Therefore, this paper proposed an IQGA to solve the problems of QGA.
1) Dynamic rotation angle adjustment strategy
The dynamic rotation angle adjustment strategy of IQGA can dynamically adjusting the rotation angle of quantum gates according to the evolutionary process. The method can greatly improve the convergence speed of the algorithm. Give a relatively large rotation angle in the early stage of the algorithm operation, as the degree of evolution increases, reduce the rotation angle gradually [7]. The selection strategy of dynamic rotation angle is shown in Table 1.
In Table 1, Xi is the i-th position of chromosome, besti is the i-th position of the current optimal chromosome, S(αiβi) is the rotating angle direction, Δθi is the rotation angle.
μ can be calculated by the following formula [6]:
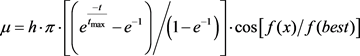 (11)
(11)
![]()
Table 1. Dynamic rotation angle adjustment strategy.
In the formula, the value of h is between 0.01 to 0.05; t is the generation; tmax is the max value of generation; f(x) is the current individual fitness; f(best) is the current optimal individual fitness.
2) The procedure of IQGA
The procedure of IQGA can be expressed as:
a) Input the raw data;
b) Initialize the population Q(t), and randomly generate multiple chromosomes encoded by quantum bits;
c) Measure the Individuals in Q(t), and get the corresponding deterministic solution P(t);
d) Carry out fitness evaluation for each individual in P(t), and get the values of all state variables;
e) Calculate the fitness function value, and use the fitness function value as the fitness value;
f) Determine whether the terminating evolution criterion is satisfied or not, if the end condition is reached, go to step g), if not, go to step h);
g) Output the optimization result, and the procedure ends;
h) Calculate the rotation angle of a new quantum gate, and generate new populations, let t = t + 1, go to step c).
The flow chart of IQGA is shown in Figure 2.
![]()
Figure 3. The load current value before using the smart commutation switch.
![]()
Figure 4. The load current value after using the smart commutation switch.
![]()
Figure 5. The comparison of current three-phase unbalance before and after using the smart commutation switch.
4. Example
Taking a 10 kV distribution transformer station area as the analysis object, the transformer model is S11-400, the number of electricity customers is about 80, the area installed 21 load commutation switch and 7 three-phase distribution control terminal.
The load current value before adding the smart commutation switch is shown in Figure 3, the load current value after using the smart commutation switch is shown in Figure 4, the comparison of current three-phase unbalance before and after using the smart commutation switch is shown in Figure 5.
From Figures 3-5, before using the smart commutation switch, the max value of three-phase current unbalance degree was 0.35, by using the smart commutation switch, the max value of three-phase current unbalance degree is 0.04 and is complied with national standards. The results from the calculating examples show that the commutation switch can reduce the three-phase current unbalance degree.
5. Conclusion
Firstly, the structure of commutation system and the advantages of the commutation switch are introduced in the paper. Secondly, the objective function and constraint condition were established and the IQGA was proposed to solve the problems of QGA in the commutation control strategy. At last, the rationality and the efficiency of the algorithm and the commutation switch were verified by the practical example.