Unicity of Meromorphic Solutions of Some Nonlinear Difference Equations

Baoqin Chen

Faculty of Mathematics and Computer Science, Guangdong Ocean University, Zhangjiang, China.

DOI: 10.4236/apm.2019.97030                

Abstract

This paper is to study the unicity of transcendental meromorphic solutions to some nonlinear difference equations. Let be a nonzero rational function. Consider the uniqueness of transcendental meromorphic solutions to some nonlinear difference equations of the form . For two finite order transcendental meromorphic solutions of the equation above, it shows that they are almost equal to each other except for a nonconstant factor, if they have the same zeros and poles counting multiplicities, when . Two relative results are proved, and examples to show sharpness of our results are provided.

Keywords

Unicity, Meromorphic Solution, Difference Equation

1. Introduction

It is well known that a given nonconstant monic polynomial is determined by its zeros. But it is not true for transcendental entire or meromorphic functions. Take ${\text{e}}^z$ and ${\text{e}}^{-z}$ for example, they are essentially different even have the same zeros, 1-value points and poles. This indicates that it is complex and interesting to determine a transcendental meromorphic function uniquely. Nevanlinna then proves his famous Nevanlinna’s 5 CM (4 IM) Theorem (see e.g. [1] [2] ):

Theorem A: Let w(z) and u(z) be two nonconstant meromorphic functions. If w(z) and u(z) share 5 values IM (4 values CM, respectively) in the extended complex plane, then $w\left(z\right)\equiv u\left(z\right)\left(w\left(z\right)=T\left(u\left(z\right)\right)\right)$ , where T is a Möbius transformation, respectively).

Here and in the following, for two nonconstant meromorphic functions w(z) and u(z), and a complex constant a, we say w(z) and u(z) share a IM (CM), if w(z)-a and u(z)-a have the same zeros ignoring multiplicities (counting multiplicities); and we say w(z) and u(z) share ∞ IM(CM), if they have the same poles ignoring multiplicities (counting multiplicities).

Our aim is to study the unicity of meromorphic solutions to the nonlinear difference equation of the form

$w\left(z+1\right)w\left(z-1\right)=R\left(z\right)w^m\left(z\right)$ , (1.1)

where R(z) is a nonzero rational function and $m\in \left\{\pm 2,\pm 1,0\right\}$ The Equation (1.1) comes from the family of Painlevé III equations which are given by Ronkainen in [3] when he classifies the difference equation

$w\left(z+1\right)w\left(z-1\right)=R\left(z,w\right),$

where R(z, w) is irreducible and rational in w and meromorphic in z. This is a natural idea which comes from the topic on the growth, value distribution and unicity on the meromorphic solutions to difference equations (see e.g. [4] [5] [6] [7] [8] ). The first result is as follows.

Theorem 1.1. Let w(z) and u(z) be two finite order transcendental meromorphic solutions to the Equation (1.1), where $m\in \left\{2,\pm 1,0\right\}$ . If w(z) and u(z) share 0, ∞ CM, then $w\left(z\right)\equiv \lambda u\left(z\right)$ , where $\lambda$ is a constant such that ${\lambda }^{2-m}=1$ .

The following examples show that all cases in Theorem 1.1. can happen, and the “CM” cannot be relaxed to “IM”.

Example 1. In the following examples, $w_j\left(z\right)$ and $u_j\left(z\right)$ share 0, ∞ CM, while $w_j\left(z\right)$ and $v_j\left(z\right)$ share 0, ∞ IM $\left(j=1,2,3,4\right)$ :

1) $u_1\left(z\right)=\tan \left(\frac{\pi z}{2}\right),w_1\left(z\right)=i{u}_1\left(z\right)$ and $v_1\left(z\right)=u_1^2\left(z\right)$ satisfy the difference equation

$w\left(z+1\right)w\left(z-1\right)=w^{-2}\left(z\right).$

here $m=-2,\lambda =i$ such that ${\lambda }^{2-\left(-2\right)}=1$ .

2) $u_2\left(z\right)={\tan }^2\left(\frac{\pi z}{3}\right){\tan }^2\left[\frac{\left(2z-1\right)\pi }{6}\right],w_2\left(z\right)={\text{e}}^{i\frac{2\pi }{5}}{u}_2\left(z\right)$ and $v_2\left(z\right)=u_2^2\left(z\right)$ satisfy the difference equation

$w\left(z+1\right)w\left(z-1\right)=w^{-1}\left(z\right).$

here $m=-1,\lambda ={\text{e}}^{\frac{2\pi i}{3}}$ such that ${\lambda }^{2-\left(-1\right)}=1$ .

3) $u_3\left(z\right)=\tan \left(\frac{\pi z}{4}\right),w_3\left(z\right)=-u_3\left(z\right)$ and $v_3\left(z\right)=i{u}_3^2\left(z\right)$ satisfy the difference equation

$w\left(z+1\right)w\left(z-1\right)=-1.$

here $m=0,\lambda =-1$ such that ${\lambda }^{2-0}=1$ .

4) $u_4\left(z\right)=\tan \left(\frac{\pi z}{6}\right)\tan \left[\frac{\pi \left(z-1\right)}{6}\right],w_4\left(z\right)=u_4\left(z\right)$ and $v_4\left(z\right)=u_4^3\left(z\right)$ satisfy the difference equation

$w\left(z+1\right)w\left(z-1\right)=-w\left(z\right).$

here $m=1,\lambda =1$ such that ${\lambda }^{2-1}=1$ .

Theorem 1.2. Let w(z) and u(z) be two finite order transcendental meromorphic solutions to the Equation (1.1), where $m\in \left\{2,\pm 1,0\right\}$ . If w(z) and u(z) share 0, ∞ CM, then

$w\left(z\right)\equiv {\text{e}}^{a_2{z}^2+a_{1}z+a_0}u\left(z\right),$ (1.2)

where $a_0,a_1,a_2$ are constants such that ${\text{e}}^{2a_2}=1$ . What is more, $w\left(z\right)\equiv u\left(z\right)$ if $w\left(z\right)-u\left(z\right)$ has a zero $z_1$ of multiplicity $\ge 3$ such that $w\left(z_1\right)=u\left(z_1\right)=c\ne 0$ .

The following example shows that all conclusions in Theorem 1.2 can happen, and the “CM” cannot be relaxed to “IM”.

Example 2. Let $u\left(z\right)=\tan \left(\pi z\right),v\left(z\right)=u^2\left(z\right)$ and $w_1\left(z\right)={\text{e}}^{\pi i{z}^2}u\left(z\right)$ , $w_2\left(z\right)={\text{e}}^{z}u\left(z\right)$ , $w_3\left(z\right)=u\left(z\right)$ . Then $w_j\left(z\right)$ and $u\left(z\right)$ share 0, ∞ CM, while $w_j\left(z\right)$ and $v\left(z\right)$ share 0, ∞ IM (j = 1, 2, 3), and they solve the equation

$w\left(z+1\right)w\left(z-1\right)=w^2\left(z\right).$

Theorem 1.3. Let w(z) and u(z) be two finite order transcendental meromorphic solutions to the Equation (1.1), where $m\in \left\{\pm 1,0\right\}$ . If w(z) and u(z) share 1, ∞ CM, then

$w\left(z\right)-1\equiv {\text{e}}^{a_{1}z+a_0}\left(u\left(z\right)-1\right),$ (1.3)

where $a_0,a_1$ are constants such that:

1) $a_1=\frac{k_1}{2}\pi i$ , when $m=0$ ; 2) $a_1=\frac{2k_2}{3}\pi i$ , when $m=-\text{1}$ ; (3) $a_1=\frac{k_3}{3}\pi i$ , when

$m=1$ , where $k_1,k_2,k_3$ are some integers. What is more, $w\left(z\right)\equiv u\left(z\right)$ if one of the following additional condition holds:

a) $w\left(z\right)-u\left(z\right)$ has a zero $z_1$ of multiplicity $\ge 2$ such that $w\left(z_1\right)=u\left(z_1\right)=0$ ;

b) there exist two constants $z_2,z_3$ such that $w\left(z_j\right)=u\left(z_j\right)\ne 1\left(j=2,3\right)$ and $z_2-z_3\cancel{\in }\mathbb{Q}$ .

Remark 1. We have tried hard but failed to provide some similar results as Theorem 1.3 for the cases $m=\pm 2$ so far.

2. Proof of Theorem 1.1

Since w(z) and u(z) are finite order transcendental meromorphic functions and share 0, ∞ CM, we see that

$\frac{w\left(z\right)}{u\left(z\right)}={\text{e}}^{p\left(z\right)},$

where $p\left(z\right)$ is a polynomial such that it is of degree $\mathrm{deg}p\left(z\right)=p\le \max \left\{\rho \left(w\right),\rho \left(u\right)\right\}.$

Next, we discuss case by case.

Case 1: m = −2. From (1.1) and (2.1) we get

$\begin{array}{l}u\left(z+1\right)u\left(z-1\right)u^2\left(z\right){\text{e}}^{p\left(z+1\right)+p\left(z-1\right)+2p\left(z\right)}\\ =w\left(z+1\right)w\left(z-1\right)w^2\left(z\right)=R\left(z\right)=u\left(z+1\right)u\left(z-1\right)u^2\left(z\right),\end{array}$

which gives

$\left({\text{e}}^{p\left(z+1\right)+p\left(z-1\right)+2p\left(z\right)}-1\right)u\left(z+1\right)u\left(z-1\right)u^2\left(z\right)\equiv 0.$

Thus, we have

${\text{e}}^{p\left(z+1\right)+p\left(z-1\right)+2p\left(z\right)}\equiv 1.$ (2.2)

Since

$\mathrm{deg}\left(p\left(z+1\right)+p\left(z-1\right)+2p\left(z\right)\right)=\mathrm{deg}p\left(z\right)=p,$

from (2.2), it is easy to find that p = 0. Therefore, there exists some constant $p_0$ , such that $p\left(z\right)\equiv p_0$ and

${\text{e}}^{4p_0}={\text{e}}^{p\left(z+1\right)+p\left(z-1\right)+2p\left(z\right)}\equiv 1.$

That is, for $\lambda ={\text{e}}^{p_0}$ , we have $w\left(z\right)\equiv \lambda u\left(z\right)$ and ${\lambda }^4=1$ .

Case 2: m = −1. Now, we obtain from (1.1) and (2.1) that

$\begin{array}{l}u\left(z+1\right)u\left(z-1\right)u\left(z\right){\text{e}}^{p\left(z+1\right)+p\left(z-1\right)+2p\left(z\right)}\\ =w\left(z+1\right)w\left(z-1\right)w\left(z\right)=R\left(z\right)=u\left(z+1\right)u\left(z-1\right)u\left(z\right).\end{array}$

With this equation and similar reasoning as in Case 1, we can deduce that $w\left(z\right)\equiv \lambda u\left(z\right)$ holds for some $\lambda$ such that ${\lambda }^3=1$ .

Case 3: m = 0. From (1.1) and (2.1), we have

$u\left(z+1\right)u\left(z-1\right){\text{e}}^{p\left(z+1\right)+p\left(z-1\right)}=w\left(z+1\right)w\left(z-1\right)=R\left(z\right)=u\left(z+1\right)u\left(z-1\right).$

Similarly, we can prove that $w\left(z\right)\equiv \lambda u\left(z\right)$ holds for some $\lambda$ such that ${\lambda }^2=1$ .

Case 4: m = 1. Now (1.1) is of the form

$w\left(z+1\right)w\left(z-1\right)=R\left(z\right)w\left(z\right).$ (2.3)

Thus,

$w\left(z+2\right)w\left(z\right)=R\left(z+1\right)w\left(z+1\right).$

It follows from these two equations above and (2.1) that

$\begin{array}{l}u\left(z+2\right)u\left(z-1\right){\text{e}}^{p\left(z+2\right)+p\left(z-1\right)}\\ =w\left(z+2\right)w\left(z-1\right)=R\left(z+1\right)R\left(z\right)=u\left(z+2\right)u\left(z-1\right),\end{array}$

with which we can show that $w\left(z\right)\equiv \lambda u\left(z\right)$ holds for some $\lambda$ such that ${\lambda }^2=1$ . However, if $w\left(z\right)\equiv -u\left(z\right)$ , we find that

$\left(-w\left(z+1\right)\right)\left(-w\left(z-1\right)\right)=u\left(z+1\right)u\left(z-1\right)=R\left(z\right)u\left(z\right)=-R\left(z\right)w\left(z\right).$ (2.4)

Combining (2.3) and (2.4), we get $R\left(z\right)w\left(z\right)\equiv 0$ , which is impossible. Thus, $\lambda =1$ .

3. Proof of Theorem 1.2

Notice that (2.1) still holds for this case. We can get from (1.1) and (2.1) that

$\frac{u\left(z+1\right)u\left(z-1\right){\text{e}}^{p\left(z+1\right)+p\left(z-1\right)}}{u^2\left(z\right){\text{e}}^{2p\left(z\right)}}=\frac{w\left(z+1\right)w\left(z-1\right)}{w^2\left(z\right)}=R\left(z\right)=\frac{u\left(z+1\right)u\left(z-1\right)}{u^2\left(z\right)}.$

Thus, we have

${\text{e}}^{p\left(z+1\right)+p\left(z-1\right)+2p\left(z\right)}\equiv 1.$ (3.1)

If $p\le 1$ , then our conclusion holds for $a_2=0$ . If $p\ge 2$ , set

$p\left(z\right)=a_p{z}^p+a_{p-1}{z}^{p-1}+\cdots +a_{1}z+a_0,$ (3.2)

where $a_p\ne 0,a_{p-1},\cdots ,a_1,a_0$ are constants.

From (3.2), we see that

$p\left(z+1\right)+p\left(z-1\right)-2p\left(z\right)=p\left(p-1\right)a_p{z}^{p-2}+q\left(z\right),$ (3.3)

where q(z) is a polynomial such that $q\left(z\right)\equiv 0$ when $p=2$ , or $\mathrm{deg}q\left(z\right)<p-2$ when $p\ge 3$ .

Suppose that $p\ge 3$ , we obtain from (3.1) and (3.3) that

$1\equiv {\text{e}}^{p\left(z+1\right)+p\left(z-1\right)+2p\left(z\right)}={\text{e}}^{p\left(p-1\right)a_p{z}^{p-2}+q\left(z\right)},$

which is impossible. Thus, $p=\text{2}$ , then from (3.1) and (3.3), we get ${\text{e}}^{2a_2}=1$ immediately. To sum up, we prove that (1.2) holds.

Next, we use $p\left(z\right)=a_2{z}^2+a_{1}z+a_0$ and prove our additional conclusion. From (1.2), we see that ${\text{e}}^{p\left(z_1\right)}=1$ .

Differentiating both sides of (1.2), we can deduce that

$p^{\prime }\left(z\right){\text{e}}^{p\left(z\right)}u\left(z\right)=w^{\prime }\left(z\right)-{\text{e}}^{p\left(z\right)}{u}^{\prime }(z)$

and

$p^{″}\left(z\right){\text{e}}^{p\left(z\right)}u\left(z\right)=w^{″}\left(z\right){\text{e}}^{p\left(z\right)}u\left(z\right)={\left(p^{\prime }\left(z\right)\right)}^2{\text{e}}^{p\left(z\right)}u\left(z\right)-2p^{\prime }\left(z\right){\text{e}}^{p\left(z\right)}{u}^{\prime }\left(z\right).$

By our assumption, (1.2}), (3.4) and the fact that ${\text{e}}^{p\left(z_1\right)}=1$ , we have

$\begin{array}{c}{p}^{\prime }\left(z_1\right)=p^{\prime }\left(z_1\right)u\left(z_1\right)=p^{\prime }\left(z_1\right){\text{e}}^{p\left(z_1\right)}u\left(z_1\right)\\ =w^{\prime }\left(z_1\right)-{\text{e}}^{p\left(z_1\right)}{u}^{\prime }\left(z_1\right)\\ =w^{\prime }\left(z_1\right)-u^{\prime }\left(z_1\right)=0.\end{array}$

Therefore, similarly, it follows from (3.5) that

$\begin{array}{c}{p}^{″}\left(z_1\right)=p^{″}\left(z_1\right){\text{e}}^{p\left(z_1\right)}u\left(z_1\right)\\ =w^{″}\left(z_1\right)-{\text{e}}^{p\left(z_1\right)}{u}^{″}\left(z_1\right)-{\left(p^{\prime }\left(z_1\right)\right)}^2{\text{e}}^{p\left(z_1\right)}u\left(z_1\right)-2p^{\prime }\left(z_1\right){\text{e}}^{p\left(z_1\right)}{u}^{\prime }\left(z_1\right)\\ =w^{″}\left(z_1\right)-u^{″}\left(z_1\right)=0.\end{array}$

As a result, we obtain

$2a_2=p^{″}\left(z_1\right)=0,2a_2{z}_1+a_1=p^{\prime }\left(z_1\right)=0,{\text{e}}^{2a_2{z}_1^2+a_0{z}_1+a_0}={\text{e}}^{p\left(z_1\right)}=1,$

that is, $a_2=a_1=0,{\text{e}}^{a_0}=1$ . Hence, $w\left(z\right)\equiv {\text{e}}^{a_2{z}^2+a_{1}z+a_0}u\left(z\right)=u\left(z\right)$ .

4. Proof of Theorem 1.3

Here, we need the lemma below, where the case that R(z) is a nonzero constant has been proved by Zhang and Yang [7] and the case that R(z) is a nonconstant rational function by Lan and Chen [8] .

Lemma 4.1. [7] [8] Let w(z) be a finite order transcendental meromorphic solution to

the Equation (1.1), where $m\in \left\{-2,\pm 1,0\right\}$ and a be a constant. Then

$\lambda \left(w-a\right)=\lambda \left(1/w\right)=\rho \left(w\right)\ge 1.$

Proof of Theorem 1.3. Since $w\left(z\right)$ and $u\left(z\right)$ are finite order transcendental meromorphic functions and share 1, ∞ CM, we see that

$\frac{w\left(z\right)-1}{u\left(z\right)-1}={\text{e}}^{p\left(z\right)},$ (4.1)

where $p\left(z\right)$ is a polynomial such that

$p\left(z\right)=a_p{z}^p+a_{p-1}{z}^{p-1}+\cdots +a_0,$ (4.2)

where $a_p\ne 0,\cdots ,a_0$ are constants and $p=\mathrm{deg}p\left(z\right)\le \max \left\{\rho \left(w\right),\rho \left(u\right)\right\}$ .

Case 1: m = 0. From (1.1) and (4.1), we obtain

$\frac{u\left(z+4\right)}{u\left(z\right)}=\frac{R\left(z+3\right)}{R\left(z+1\right)}:=R_1\left(z\right)$ (4.3)

and

$\frac{{\text{e}}^{p\left(z+4\right)}\left(u\left(z+4\right)-1\right)+1}{{\text{e}}^{p\left(z\right)}\left(u\left(z\right)-1\right)+1}=\frac{w\left(z+4\right)}{w\left(z\right)}=\frac{R\left(z+3\right)}{R\left(z+1\right)}=R_1\left(z\right),$ (4.4)

where $R_1\left(z\right)$ is a rational function. Combining (4.1}), (4.3) and (4.4), we have

$\left({\text{e}}^{p\left(z+4\right)}-{\text{e}}^{p\left(z\right)}\right)R_1\left(z\right)\left(u\left(z\right)-1\right)=\left(1-R_1\left(z\right)\right)\left({\text{e}}^{p\left(z+4\right)}-1\right).$ (4.5)

Now, if ${\text{e}}^{p\left(z+4\right)}\cancel{\equiv }{\text{e}}^{p\left(z\right)}$ , then $p\ge 1$ and it follows from (4.5) that

$u\left(z\right)=\frac{1-R_1\left(z\right)}{R_1\left(z\right)}\frac{1-{\text{e}}^{-p\left(z+4\right)}}{1-{\text{e}}^{p\left(z\right)-p\left(z+4\right)}}+1.$ (4.6)

Notice that $\mathrm{deg}\left(p\left(z\right)-p\left(z+4\right)\right)\le p-1$ . From (4.6), we can find that

$\lambda \left(u-1\right)=p>p-1\ge \rho \left(1-{\text{e}}^{p\left(z\right)-p\left(z+4\right)}\right)\ge \lambda \left(\frac{1}{u}\right).$

This is a contradiction to the conclusion of Lemma 4.1. Thus, ${\text{e}}^{p\left(z+4\right)}\equiv {\text{e}}^{p\left(z\right)}$ . From (4.2) there exists some integer $k_1$ such that

$2k_1\pi i=p\left(z+4\right)-p\left(z\right)=4p{a}_p{z}^{p-1}+\cdots ,$

which yields obviously that $p=1$ . Therefore, we see that

$a_p=a_1=\frac{k_1}{2}\pi i$ and hence $p\left(z\right)=\frac{k_1}{2}\pi iz+a_0$ for some constant $a_0$ .

Case 2: m = −1. Now (1.1) is of the form

$u\left(z+1\right)u\left(z-1\right)u\left(z\right)=R\left(z\right),$

which gives

$\frac{u\left(z+3\right)}{u\left(z\right)}=\frac{R\left(z+2\right)}{R\left(z+1\right)}:=R_2\left(z\right).$

With this equation and a similar arguing as in Case 1, we can prove that $p\left(z\right)=\frac{2k_2}{3}\pi iz+a_0$ for some integer $k_2$ and some constant $a_0$ .

Case 3: m = 1. Now (1.1) is of the form

$u\left(z+1\right)u\left(z-1\right)=R\left(z\right)u\left(z\right),$

which gives

$u\left(z+3\right)u\left(z\right)=R\left(z+2\right)R\left(z+1\right).$

And hence we have

$\frac{u\left(z+6\right)}{u\left(z\right)}=\frac{R\left(z+5\right)R\left(z+4\right)}{R\left(z+2\right)R\left(z+1\right)}:=R_3\left(z\right).$

It follows this equation that $p\left(z\right)=\frac{k_3}{3}\pi iz+a_0$ for some integer $k_3$ and some constant $a_0$ , and (1.3) holds.

Now, if $w\left(z\right)-u\left(z\right)$ has a zero $z_1$ of multiplicity $\ge 2$ such that $w\left(z_1\right)=0$ , then from (4.1), we see that ${\text{e}}^{p\left(z_1\right)}=1$ .

Rewrite (4.1) as the form

$w\left(z\right)-1={\text{e}}^{p\left(z\right)}\left(u\left(z\right)-1\right).$

Differentiating both sides of the equation above, we have

$p^{\prime }\left(z\right){\text{e}}^{p\left(z\right)}\left(1-u\left(z\right)\right)={\text{e}}^{p\left(z\right)}{u}^{\prime }\left(z\right)-w^{\prime }\left(z\right).$

Since $z_1$ is a zero of 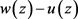with multiplicity 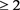such that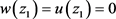, from the fact that 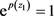and (4.7), we find that

Thus, 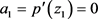, and hence. This implies that.

Finally, we discuss the Case 2). Since and, then from (4.1), we can deduce that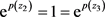. Therefore, there exists an integer 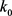such that

If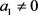, from the equation above, considering each form of 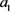for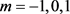, we can find that must be a nonzero rational number. This contradicts our assumption that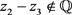. Thus, and hence. This gives again.

5. Conclusion

It is shown that the finite order transcendental meromorphic solution of the Equation (1.1) is mainly determined by its zeros (or 1-value points) and poles. Examples are provided to show sharpness of our results.

Acknowledgements

The author is very appreciated for the editors and reviewers for their constructive suggestions and comments for the readability of this paper.

Funding

This work was supported by the Natural Science Foundation of Guangdong Province (2018A030307062).

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Laine, I. (1993) Nevanlinna Theory and Complex Differential Equations. In: de Gruyter Studies in Mathematics, Walter de Gruyter, Berlin, New York.
[2]	Yang, C.C. and Yi, H.X. (2003) Uniqueness Theory of Meromorphic Functions. Kluwer Academic Publishers, Dordrecht.
[3]	Ronkainen, O. (2010) Meromorphic Solutions of Difference Painlevé Equations. Annales Academiae Scientiarum Fennicae Mathematica, 155, 1-59.
[4]	Chen, Z.X. (2014) Complex Differences and Difference Equations. Science Press, Beijing.
[5]	Cui, N. and Chen, Z.X. (2017) Uniqueness for Meromorphic Solutions Sharing Three Values with a Meromorphic Function to Some Linear Difference Equations. Chinese Annals of Mathematics, Series A, 38, 13-22.
[6]	Lü, F., Han, Q. and Lü, W.R. (2016) On Unicity of Meromorphic Solutions to Difference Equations of Malmquist Type. Bulletin of the Australian Mathematical Society, 93, 92-98. https://doi.org/10.1017/S0004972715000787
[7]	Zhang, J.L. and Yang, L.Z. (2014) Meromorphic Solutions of Painlevé III Difference Equations. Acta Mathematica Sinica, 57, 181-188.
[8]	Lan, S.T. and Chen, Z.X. (2014) On Properties of Meromorphic Solutions of Certain Difference Painlevé Equations. Abstract and Applied Analysis, 2014, Article ID: 208701. https://doi.org/10.1155/2014/208701