Generation of Vertical Fine Structure by Internal Waves in a Shear Flow ()
1. Introduction
The fine vertical structure of hydrophysical fields in the ocean was discovered in the second half of the last century after the creation of high - resolution sounding equipment [1] [2] [3] [4] . It was discovered that the vertical profiles of temperature and salinity are strongly indented vertically. As a rule, layers with low temperature and salinity gradients alternate with layers, where gradients of these characteristics have sufficiently large values [5] . Until the mid-70s of the last century, internal waves were considered as the main source of generation of a vertical fine structure away from the frontal zones and shores. Perturbations of temperature, salinity and density profiles caused by short-period internal waves were considered as a reversible fine structure due to the kinematic effect of internal waves [5] . However, breaking of internal waves leads to the generation of turbulence patches, the evolution of which leads to irreversible fine and microstructure in the form of “fossil turbulence” pancakes [5] [6] . Hydrodynamic instability of internal waves and currents generates intermittent turbulence and microstructure in the ocean [6] [7] [8] .
The double diffusion mechanism is realized when the temperature and salinity simultaneously decrease (or increase) with depth [9] . Stratification at double diffusion remains stable. If the temperature and salinity decrease with depth, it is possible to develop a convection type of “salt fingers”. In-situ optical observation led to the discovery in the high-gradient layers “salt fingers” cells [10] [11] . The observed stepped structure is supported by turbulent convection in quasi-homogeneous layers caused by mass transfer through high-gradient layers by “salt fingers”.
In the areas of fronts, the “intrusive” mechanism is possible, when there is a mutual penetration of waters with different
characteristics (T-temperature, S-salinity). The fine structure of the “intrusion type” has temperature and salinity inversions with stable stratification [12] . Sometimes, against the background of such inversions, stepped structures develop due to the mechanism of double diffusion.
The most typical situation is when the temperature decreases with depth and salinity increases. In this case, the “double diffusion” does not work and internal waves make a main contribution to the generation of vertical fine structure in the ocean.
Internal waves in the ocean play an important role in the dynamics of stratified deep layer. As a rule, the propagation of internal waves occurs at space-inhomogeneous flows, with the interaction of internal waves with currents. There are two effects that lead to wave energy dissipation. The first is to capture and focus the internal waves by a horizontally inhomogeneous picnocline [13] , which plays a role of a waveguide for internal wave. During the focusing, wave amplitude increases up to the manifestation of nonlinear effects and energy dissipation. The second effect is wave energy dissipation on the critical layer, where the phase velocity is equal to the flow velocity [14] . In both cases, small-scale turbulence is generated. Vertical ocean exchange is usually associated with small-scale turbulence, whose energy sources should also include hydrodynamic instability of flows and breaking of internal waves [5] [15] . It should be noted that turbulence is strongly suppressed by stratification in the pycnocline and the question of the contribution of internal waves to the vertical exchange becomes relevant.
Nonlinear effects at the propagation of packets of internal waves are manifested in the generation of average on a wave time scale current [16] [17] and corrections to density [17] [18] [19] , which is proportional to the square of the wave amplitude. The vertical velocity of the flows induced by the packet on the leading and trailing edges of the packet has different signs and there is no integral wave transfer along the vertical. After passing of wave packet the unperturbed stratification profile is restored and the vertical fine structure of the density field generated by the wave is thus reversible.
However, as shown below for inertia-gravity internal waves, the vertical wave mass flux is non-zero in the presence of a flow whose velocity component transverse to the wave propagation direction depends on the vertical coordinate. The vertical component of the Stokes drift velocity is non-zero too and contributes to the wave transfer. The presence of a vertical wave flux of mass leads to the generation of irreversible fine structure.
2. Problem Definition
We will consider the free internal waves in an infinite pool of constant depth by using the Boussinesq approximation and taking into account the rotation of the Earth. The two components of the mean flow velocity depend on the vertical coordinate. In the linear approximation, the boundary value problem for the vertical velocity amplitude has complex coefficients; therefore, its solution is a complex function, and the wave frequency value is also complex (i.e., there occurs a weak attenuation of the wave). The Stokes drift velocity, the wave fluxes of mass, and the corrections to density that do not oscillate on the time scale of the wave are found in the second order in the amplitude of the wave.
The system of hydrodynamic equations for wave disturbances in the Boussinesq approximation has the form
(1)
(2)
(3)
(4)
(5)
Here we use the coordinate system
where the z-axis is directed upwards;
are respectively two horizontal and vertical components of the wave flow velocity,
and P are wave perturbations of density and pressure, H is the depth of the sea,
is the average density profile, f is the Coriolis parameter,
are two components of the mean velocity flow, g is
acceleration of gravity and the action of the operator
is determined by the formula
At the sea surface (z = 0), we use a rigid-lid boundary condition which filters the internal waves out from the surface waves [20]
(6)
At the bottom, we satisfy the non-flow condition
(7)
3. Linear Approximation
In the linear approximation, the solutions can be written in the form
,
,
,
, (8)
where
is a complex conjugate term, A is the amplitude factor,
is a phase of the wave;
; k is horizontal wave number,
is wave frequency. It is assumed that the wave propagates along the x-axis.
After substituting (8) into system (1) - (5), follows coupling of the amplitude functions
with
,
, (9)
,
, (10)
, (11)
function
satisfies the equation
(12)
where
is the square of Brunt-Väisälä frequency.
Boundary conditions for
,
(13)
,
(14)
Equation (12) has complex coefficients, the imaginary part of which is small, so let us turn to dimensionless variables (the dashed line denotes dimensionless physical quantities)
(15)
where
is characteristic wave frequency,
is a characteristic value of the flow velocity which is transverse to the wave propagation direction.
Equation (12) then takes the form:
(16)
is a small parameter. The imaginary part of the coefficients in Equation (16) is the order of , therefore the imaginary part of the solution
, therefore the imaginary part of the solution  is also proportional
is also proportional , i.e. the solution of Equation (16) is represented in the form [21] :
, i.e. the solution of Equation (16) is represented in the form [21] :
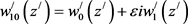 (17)
(17)
where 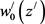 and
and 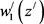 are real functions. The frequency is also expressed as a parameter expansion
are real functions. The frequency is also expressed as a parameter expansion 
 (18)
(18)
then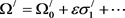 . After substituting (17), (18) into (12), we obtain boundary value problems for
. After substituting (17), (18) into (12), we obtain boundary value problems for 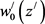 and
and . Function
. Function 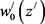 satisfies the Equation (up to terms
satisfies the Equation (up to terms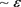 ):
):
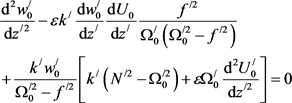 (19)
(19)
The boundary conditions for 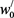
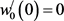 ,
,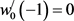 . (20)
. (20)
Function 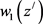 satisfies the Equation (up to terms
satisfies the Equation (up to terms![]() ):
):
![]() (21)
(21)
where
![]()
The boundary conditions for ![]()
![]() ,
,![]() . (22)
. (22)
After the transition to dimensional variables, Equation (19) takes the form:
![]() (23)
(23)
where ![]() is wave frequency with Doppler shift.
is wave frequency with Doppler shift.
Equation (23) should be supplemented by boundary conditions:
![]() ,
,![]() . (24)
. (24)
The boundary-value problem (23), (24) in the absence of flow ![]() has a countable set of eigenfunctions, a set of modes. Moreover, to each value of the wavenumber k corresponds to a certain frequency value
has a countable set of eigenfunctions, a set of modes. Moreover, to each value of the wavenumber k corresponds to a certain frequency value ![]() corresponding to the given mode. When
corresponding to the given mode. When ![]() the discrete spectrum of real eigenfrequencies may not exist [22] . This is connected with the singularities in Equation (23) with
the discrete spectrum of real eigenfrequencies may not exist [22] . This is connected with the singularities in Equation (23) with ![]() and
and ![]() (hydrodynamically stable flows are considered). In the presence of singular
(hydrodynamically stable flows are considered). In the presence of singular ![]() there is a critical layer [23] , where the phase velocity of the wave is equal to the flow velocity. With allowance for the rotation of the Earth, the singularity shifts to a level where
there is a critical layer [23] , where the phase velocity of the wave is equal to the flow velocity. With allowance for the rotation of the Earth, the singularity shifts to a level where ![]() [24] . The effect of this singularity on the dispersion curves is illustrated by the calculations given below.
[24] . The effect of this singularity on the dispersion curves is illustrated by the calculations given below.
Let![]() ,
, ![]() , then Equation (23) can be written in the form:
, then Equation (23) can be written in the form:
![]() (25)
(25)
Equation (25) leads to a selfadjoint form, multiplying both sides of the equation by![]() :
:
![]() (26)
(26)
here![]() .
.
After the transition to dimensional variables, Equation (21) is transformed into the form
![]() (27)
(27)
where
![]()
The boundary conditions for the function ![]()
![]() ,
, ![]() . (28)
. (28)
We multiply both sides of the linear inhomogeneous Equation (27) by the function ![]() we obtain on the left-hand side a selfadjoint operator, the same as in the linear homogeneous Equation (26):
we obtain on the left-hand side a selfadjoint operator, the same as in the linear homogeneous Equation (26):
![]() , (29)
, (29)
where ![]()
The solvability condition for the boundary value problem (28), (29) [25] :
![]() (30)
(30)
Hence the expression for ![]()
![]() (31)
(31)
where
![]()
![]()
The value ![]() is purely imaginary, i.e.
is purely imaginary, i.e. ![]() is the decrement of the wave attenuation.
is the decrement of the wave attenuation.
4. Nonlinear Effects
Stokes drift velocity of fluid particles is determined by the formula [26]
![]() , (32)
, (32)
where ![]() is the field of wave Euler velocities and the bar above denotes averaging over the wave period.
is the field of wave Euler velocities and the bar above denotes averaging over the wave period.
The vertical component of Stokes drift velocity determined by the formula [27]
![]() (33)
(33)
where![]() ,
, ![]() at the initial time at
at the initial time at![]() .
.
In the presence of an average flow in which component of velocity ![]() transverse to the wave propagation depends on the vertical coordinate the value of
transverse to the wave propagation depends on the vertical coordinate the value of ![]() is distinct from zero.
is distinct from zero.
The vertical wave mass flux is determined by the formula
![]() (34)
(34)
The presence of a vertical wave flux of mass leads to an irreversible deformation of the density field, which can be considered as a vertical fine structure generated by a wave. The equation for the non-oscillating on the time scale of the correction to the average density ![]() up to terms that are quadratic in the amplitude of the wave has the form
up to terms that are quadratic in the amplitude of the wave has the form
![]()
hence
![]() (35)
(35)
Integrate Equation (35) in time
![]() (36)
(36)
Substituting ![]() (34) and the vertical component of the Stokes drift velocity
(34) and the vertical component of the Stokes drift velocity ![]() (33) into (36) we obtain after integration
(33) into (36) we obtain after integration
![]() (37)
(37)
where![]() ,
, ![]()
Passing to the limit in (37) for ![]() taking into account that
taking into account that ![]() we find
we find ![]()
![]() (38)
(38)
The ![]() value which depends on the vertical coordinate is a correction to the mean density that does not oscillate on the time scale of the wave is a vertical fine structure generated by the wave. A non-oscillating correction to density proportional to the square of the current wave amplitude, was determined in [17] [18] [19] , after passing the wave packet the unperturbed stratification profile is restored and the fine structure is reversible. Correction (38) is proportional to the square of the maximum amplitude of the wave and is an irreversible fine structure generated by the wave.
value which depends on the vertical coordinate is a correction to the mean density that does not oscillate on the time scale of the wave is a vertical fine structure generated by the wave. A non-oscillating correction to density proportional to the square of the current wave amplitude, was determined in [17] [18] [19] , after passing the wave packet the unperturbed stratification profile is restored and the fine structure is reversible. Correction (38) is proportional to the square of the maximum amplitude of the wave and is an irreversible fine structure generated by the wave.
5. Results of Calculations
5.1. North-Western Shelf of the Black Sea
We calculate the mass wave flux for the internal waves observed during the full-scale experiment in the third stage of the 44th voyage of the research vessel Mikhail Lomonosov on the North-Western shelf of the Black Sea. Figure 1 presents four realizations of elevations of temperature isolines obtained from GRAD instruments (gradient-distributed temperature sensors) [28] .
The first device was located in the 5 - 15 m layer, the second in the layer 15 - 25 m, the third in the layer 25 - 35 m, the fourth in the layer 35 - 60 m. It is easy to see that powerful oscillations with a period of 15 min in the 25 - 60 m layer are in antiphase with oscillations in the 15 - 25 m layer, which indicates the presence of the second mode.
The vertical profiles of the two components of the flow velocity are shown in Figure 2(a), Brunt-Väisälä frequencies in Figure 2(b), eigenfunctions of the second mode in Figure 2(c). The boundary value problem (23), (24) for internal waves is solved numerically by the implicit Adams scheme of the third order of accuracy. The wave number of the 15-minute internal waves of the second mode is 0.032 rad/m.
The normalizing factor ![]() is found from the known maximum amplitude of the vertical displacements ~0.5 м. To do this we express the vertical displacement
is found from the known maximum amplitude of the vertical displacements ~0.5 м. To do this we express the vertical displacement ![]() using the ratio
using the ratio ![]()
![]()
this implies
![]()
Figure 1. Time course of vertical displacements of temperature isolines.
![]() .
.
Thus, the amplitude of vertical displacements is proportional to![]() . Extremes of the function
. Extremes of the function ![]() correspond to the maximum vertical displacements from the experimental data (Figure 1, Figure 2(c)), i.e. in the experiment, the second mode was observed. The wavelength of fifteen-minute internal waves of the second mode is 196 m. The dispersion curves of the first two modes are shown in Figure 3(a). If the flow is not taken into account, then the dispersion curves in the low-frequency region begin with a minimum frequency that is almost equal to the inertia frequency (Figure 3(b)). When the flow is taken into account, due to the influence of the singularity
correspond to the maximum vertical displacements from the experimental data (Figure 1, Figure 2(c)), i.e. in the experiment, the second mode was observed. The wavelength of fifteen-minute internal waves of the second mode is 196 m. The dispersion curves of the first two modes are shown in Figure 3(a). If the flow is not taken into account, then the dispersion curves in the low-frequency region begin with a minimum frequency that is almost equal to the inertia frequency (Figure 3(b)). When the flow is taken into account, due to the influence of the singularity ![]() the dispersion curves are cut off in the low-frequency region (Figure 3(a)). The minimum frequency of the first mode corresponds to 1.13 × 10−4 rad/s, for the second mode 3.49 × 10−4 rad/s (for comparison we point out that the Coriolis frequency is equal to 1.048 × 10−4 rad/s). The dispersion curves are cut off due to the influence of critical layers where the frequency of the wave with Doppler shift is equal to the inertial one.
the dispersion curves are cut off in the low-frequency region (Figure 3(a)). The minimum frequency of the first mode corresponds to 1.13 × 10−4 rad/s, for the second mode 3.49 × 10−4 rad/s (for comparison we point out that the Coriolis frequency is equal to 1.048 × 10−4 rad/s). The dispersion curves are cut off due to the influence of critical layers where the frequency of the wave with Doppler shift is equal to the inertial one.
![]() (a)
(a) ![]() (b)
(b) ![]() (c)
(c)
Figure 2. Vertical profiles of components of flow velocity (a), Brunt-Väisälä frequency (b) and eigenfunction of 15-minute internal waves of the second mode (c).
![]() (a)
(a) ![]() (b)
(b)
Figure 3. Dispersion curves of the first (1) and second (2) modes in the presence of a flow (a) and without (b).
5.2. Deep-Sea Part of the Black Sea
In the deep-water area of the North-Western part of the Black Sea, above the continental slope, there is a jet of the Main Black sea current (MBC). The Brunt-Väisälä frequency profile, the two components of the flow velocity and the eigenfunction of the fifteen-minute internal wave of the second mode are shown in Figure 4. The data of soundings of the LADCP (Lowered Acoustic Doppler Current Profiler) [29] are used.
The dispersion curves of the first two modes are shown in Figure 5(a). Figure 5(b) shows the dispersion curves without flow. Comparison with Figure 5(a) shows that under the influence of the flow dispersion curves at large wave numbers begin to bend (this effect was noted in [30] ). For negative wave numbers, this effect is not observed but the dispersion curves are cut off in the low-frequency region which is again due to the influence of critical layers where the frequency of the wave with the Doppler shift is equal to inertial. Dispersion curves of the first two modes for negative k are presented as functions of the module k on Figure 5(c).
The boundary value problem for determining the function ![]() (27), (28) is solved numerically by the implicit Adams scheme of the 3rd order of accuracy; the only solution is found orthogonal to
(27), (28) is solved numerically by the implicit Adams scheme of the 3rd order of accuracy; the only solution is found orthogonal to ![]() and the damping decrement of wave
and the damping decrement of wave ![]() from (31). For the 15-minute internal waves of the second mode, the damping factor is equal to
from (31). For the 15-minute internal waves of the second mode, the damping factor is equal to ![]() rad/s in shallow water and
rad/s in shallow water and ![]() rad/s at a great depth.
rad/s at a great depth.
Vertical wave fluxes of mass ![]() (34), normalized to the square of the wave amplitude, are compared in shallow water and at great depth for the first mode of 15-minute internal waves in Figure 6(a), for the second mode in Figure 6(b). For the first mode, the wave fluxes are comparable in magnitude and the flux maxima are reached in the pycnocline. The second mode is dominated by the flux for a larger depth (dashed curve, Figure 6(b)).
(34), normalized to the square of the wave amplitude, are compared in shallow water and at great depth for the first mode of 15-minute internal waves in Figure 6(a), for the second mode in Figure 6(b). For the first mode, the wave fluxes are comparable in magnitude and the flux maxima are reached in the pycnocline. The second mode is dominated by the flux for a larger depth (dashed curve, Figure 6(b)).
![]()
Figure 4. Vertical profiles in the deep-sea part: Brunt-Väisälä frequency (a); components of flow velocity, U0, V0 (b); eigenfunction of 15-minute internal waves of the second mode (c).
![]()
Figure 5. Dispersion curves of the first (1) and second (2) modes in the deep-water part of the sea in the presence of a flow (a) and without flow (b); for negative wave numbers in the presence of flow (c).
![]() (a)
(a) ![]() (b)
(b)
Figure 6. Vertical wave fluxes of mass in shallow water (continuous) and for great depth (dashed) for the first mode—(a) and the second mode—(b).
The total vertical wave mass flux consists of the flux ![]() (34) and the flux due to the vertical velocity component of the Stokes drift
(34) and the flux due to the vertical velocity component of the Stokes drift![]() . Comparison of total fluxes for the first two modes with corresponding turbulent flux
. Comparison of total fluxes for the first two modes with corresponding turbulent flux ![]() is shown in Figure 7 for great depth. Turbulent flux is
is shown in Figure 7 for great depth. Turbulent flux is
determined by the formula![]() . The coefficient of vertical
. The coefficient of vertical
turbulent exchange is estimated by the formula ![]() m2/s,
m2/s, ![]() corresponds to the Brunt-Väisälä frequency per cycle/h [31] . The second mode dominates in the upper 100-meter layer, the wave flux of the first mode dominates deeper (Figure 7). Wave fluxes exceed in absolute magnitude the turbulent flux.
corresponds to the Brunt-Väisälä frequency per cycle/h [31] . The second mode dominates in the upper 100-meter layer, the wave flux of the first mode dominates deeper (Figure 7). Wave fluxes exceed in absolute magnitude the turbulent flux.
The vertical density profile is shown in Figure 8(a). The definition of a correction to a mean density ![]() (38) that does not oscillate on a time scale of the wave includes a value
(38) that does not oscillate on a time scale of the wave includes a value ![]() that is exactly equal
that is exactly equal ![]() at the initial time instant.
at the initial time instant.
The non-oscillating correction to the average density (38), normalized to the square of the wave amplitude, is shown in Figure 8(b) and is a fine vertical structure generated by a wave that is irreversible, and does not introduce inversions in the field of average density.
A comparison of the non-oscillating corrections to the density ![]() normalized to a square wave amplitude in shallow water and at a larger depth for 15-minute internal waves is shown in Figure 9(a) for the first mode and in Figure 9(b) for the second. In shallow water, the value
normalized to a square wave amplitude in shallow water and at a larger depth for 15-minute internal waves is shown in Figure 9(a) for the first mode and in Figure 9(b) for the second. In shallow water, the value ![]() is greater.
is greater.
Non-oscillating corrections to the Brunt-Väisälä frequency ![]() normalized to the square of the amplitude of the wave for the 15-minute internal waves is shown in Figure 10(a), the first mode, Figure 10(b), the second mode. Comparison with the fine structure of Brunt-Väisälä frequency
normalized to the square of the amplitude of the wave for the 15-minute internal waves is shown in Figure 10(a), the first mode, Figure 10(b), the second mode. Comparison with the fine structure of Brunt-Väisälä frequency ![]() according to the measurements (Figure 10(c)) shows that the contribution of internal waves is evident in the pycnocline, and the scale of the generated wave irreversible fine structure —10 - 20 m is observed.
according to the measurements (Figure 10(c)) shows that the contribution of internal waves is evident in the pycnocline, and the scale of the generated wave irreversible fine structure —10 - 20 m is observed.
![]()
Figure 7. Comparison of total wave and turbulent (3) mass fluxes for the first (1) and second (2) modes.
![]() (a)
(a) ![]() (b)
(b)
Figure 8. Vertical profiles of average density (a) and corrections to density (b) that do not oscillate on the time wave scale for the first (1) and second (2) modes.
![]() (a)
(a) ![]() (b)
(b)
Figure 9. Comparison of non-oscillating corrections to density in shallow water (1) and for large depth (2) for the first mode (a) and for the second mode (b).
![]() (a)
(a) ![]() (b)
(b) ![]() (c)
(c)
Figure 10. A non-oscillating correction on the time scale of the wave to the Brunt-Väisälä frequency for the first mode (a), for the second mode (b); the fine structure of the frequency of Brunt-Väisälä (c).
6. Conclusions
The vertical wave mass flux is different from zero for inertia-gravity internal waves in a two-dimensional vertically non-uniform flow, when the component of the flow velocity transverse to the direction of wave propagation depends on the vertical coordinate. The vertical component of the Stokes drift velocity is also nonzero and makes a main contribution to the wave transfer.
Total vertical wave mass flux exceeds the turbulent ones. The wave mass flux leads to a non-oscillating on the time scale of the wave correction to the average density, which is irreversible, i.e. to the fine structure generated by the wave. In shallow water, this correction is greater than in the deep-sea part of the sea with the same wave amplitude. The vertical scale of the Brunt-Väisälä frequency fine structure generated by the wave corresponds to the observed one. It is shown that dispersion curves are cut off in the low-frequency domain due to the influence of critical layers, where the frequency of the wave with the Doppler shift is equal to the inertial one.
Acknowledgements
The authors are grateful to Morozov A.N. for the presented experimental material on the deep-sea part. The work was carried out as part of the state assignment on the subject No. 0827-2019-0003 “Fundamental studies of oceanological processes determining the state and evolution of the marine environment under the influence of natural and anthropogenic factors, based on observation and modeling methods” (code “Oceanological processes”).