1. Introduction
The Universe consists in mass and energy, in structures not violating the basic laws of mathematical physics. While the spatial size of universe is still unknown, it is possible to speculate on the observable universe only, then implying existence of an observer. Depending on size of the observable universe and relative scale of the observer, the Universe of particular size is viewed in superimposing scales. Hence scale and size are the open questions.
Paradoxically, the observable Universe, without human observer viewed himself on a sufficiently large scale, is not complying with the cosmological principle requirements. Due to this incosistency, sufficiently large structures cannot exist. Explicitly, the observer has to be of the same scale as the observable universe is, following the cosmological principle. In other words, the observer and the observable universe are self-entangled in the cosmological principle.
To get them disentangled and to avoid ulterior speculations, the World at particular size will be referred to as the observable universe with an observer included, independly on their (universe and/or observer) size and scale. Subsequently, the following principle is postulated.
The univers’ principle is stated as: “Viewing on a sufficiently large World of particular size, the properties of underlying observable universe at some different scale are the same for all potential observers”.
This principle contains an implicit qualification and some testable consequences not discussed in here.
1.1. Scale Model of the Universe
Scale model of the entire Universe is lacking because of the sheer size of it: one cannot reasonably create the model including all the components from atom to supercluster, and simultaneously scales their distances and sizes [1] .
The difficulty is overcome by examining the Universe by universes, thus at different realms. We start at Planck size object and zoom out to the observable Universe, throughout the superimposed worlds. In each step of the way, we use the room we are in to physically represent a realm of particular universe. Looking for smart materials that can represent the objects within each realm, all to scale, a common 1-D profile across all the universes could be built up, towards a scale model of the Universe as a whole, like the particle in a box model in quantum mechanics.
The object in a box model of the World is under the rule of second order differential equation: either Schrodinger’s, or Laplace’s or else Helmholtz’s ones. Separation of variables leads to a new (phantom) variable.
As to the Universe as a whole, this is a plural superimposition of underlying universes, in succession. For instance, the cosmos, the layered earth, a rock, an atom ..., all of them are homogeneous on some scale.
To understand more, a dynamic analysis of these systems is needed, this would show how energy flows across both spatial scales and time. Fortunately, this type of analysis is already performed for the geophysical distant soundings over a horizontally stratified earth. The multiscale concepts used in geophysical scattering theory, especially in DC field, have a tread deserving a sweeping statement, however.
1.2. Self-Entanglement, Disentaglement and Complexity
Following the gravity force, the masses are structured so is the energy. The observable universe together with the observer, both on sufficiently large scale, succeeds in their self-entanglement and paradoxical inconsistency. For consistency, the observable universe and the observer have to be on different scale/size provided the cosmological principle is preserved as an approximation in a limit. The point is the universal principle itself.
Consequently, the deduction is: “All constituent at hand (size and scale, homogeneity and heterogeneity, and possibly others) are self-entangled components”. Our proposal for the disentaglement is superimposition out of complexity.
Complex systems are based on relationships, and their properties of self-organization, interconnections and evolution. They are emergent phenomena in the sense that they are the spontaneous outcome ot the interactions among the many constituent units with unexpected properties and regularities. Hence they are like the designed smart materials that have one or more properties that can be significantly changed in a controlled fashion by external stimuli, such as electric or magnetic fields, or light.
2. On Superimposition through Complexity
DC geoelectric theory goes into details of anisotropy and homogeneity throughout pseudo-, macro- and micro-anisotropy.
Background. Energy propagating throughout a medium undergoes multiple backward and forward reflections at the inhomogeneities. Resulting total travel time is greater when compared to propagation in homogeneous medium. In a sense, instead of inhomogeneities, one may alternatively and equivalently assume homogeneous medium and the space expanding. In electrical soundings over horizontally stratified earth the equivalence of differently layered media is known since early days of the method [2] [3] . The effect of resistivity sounding at the surface of a massive layering is the same as that for a finely layered structure provided that depth scale is stretched at each point by the local value of the so-called pseudoanisotropy coefficient and, in addition, the resistivity is specified as a kind of average resistivity [4] [5] . This effect of equivalence has been confirmed in a multitude of geophysical cases (see also the sub-section 2.2. Superimposing Scales below).
In geoelectric prospecting over horizontal layering it is up to standard to take this effect into account. Its exposition is a firm subject of geoelectrical monographs, and textbooks [6] .
Rationale. In geophysical investigation of horizontally stratified earth the inhomogeneous media are studied under different scales. There are at least two scales involved: 1) the scale of inhomogeneities (microscale), 2) less detailed scale (macroscale) related with the size of a region under investigation.
Horizontal stratification implies material property (proper impedance) varying in one particular direction. It is a rough and frequent approximation in many geophysical cases. A possible generalization is the spherical stratification under cosmological principle or else a box model of stratification considered as a one-dimensional system. In perpendicular directions the proper impedance being constant, this aspect of directional nonuniformity finds its expression in geophysical notion of pseudoanisotropy.
Of particular interest is a class of finely layered media exhibiting a repetitive or cyclic structure (proper impedance evolving between high and low values). Following geophysical theory, such pseudoanisotropic media are reparametrized under cumulative transformation, to get a massive layering. The rationale for use of these transformations is based on the knowledge that for cyclic media the transformed impedance is specified as pseudoimpedance (kind of mean impedance), and the scale is stretched by an overall value of the so-called pseudoanisotropy coefficient.
For a given cyclic pseudoanisotropic medium there exists a homogeneous isotropic medium that behaves, in the limit, exactly as does the given medium under the same excitation. This is to mean that a medium, which is viewed in the microscale as cyclic pseudoanisotropic, appears as a homogeneous medium when viewed in a macroscale. This is accompanied by distance contraction.
Physical basis. Geophysical static theory of cyclic stratified media [5] [7] [8] is generalized or modified in this note in various aspects. In substance, the framework is completed by time domain, and the medium is considered to have a repetitive (cyclic) structure in all directions.
It is worth noting that the formulation developed for horizontally stratified (one dimensional) media is applicable to general situations when proper impedance vary in space (three dimensions). To this end the medium is assumed to be discretized in all directions, and the results, having no side effects and relative to a facultative direction, could be generalized to all the directions.
If medium viewed in a macroscale exhibits the pseudoimpedance and contraction coefficient which are both constant over a region of interest, it is said to be pseudohomogeneous. The rationale for studying such media is a multitude of geophysical observations transportable to 3-D space. The pseudohomogeneity in 3-D approach might be an inherent property of the media of physical interest, provided that the micro- and macro-scales are sufficiently different. This expectation is based on cumulative nature of the transformation involved as well as on isotropy postulated for largest regions.
Governing equation. To conceptualize the problem, the governing equation is taken in the form of scalar wave equation. For a time harmonic field U, we have
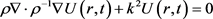 (1)
(1)
when U(r, t) can be either Ux, Uy, or Uz field component, and k = ω*/v.
The above is the Helmholtz wave equation for an inhomogeneous, isotropic, and source-free medium. In addition, proper impedance, ρ(r), and wave velocity, v(r), are both functions of position,
.
Following classical theory, in a stock-still system there is no anomalous frequency, that is to say ω* is the same as wave frequency ω (ω* = ω). When Doppler shift, ω* = ωH, is observed, we may define v* = v/H, that is to say k = ω/v*. In this case v* takes interpretation in terms of moving source and/or expanding medium. Alternative interpretation of anomalous frequency is just the point of this note.
Reparametrization. We consider stratified medium, locally (in microscale) materialized through proper impedance varying possibly in all directions [5] [8] [9] [10] but we are considering variations in only one direction, that is to say ρ(r). Let a larger region of size W be investigated by an observer located at the origin, where the cumulative parameters are introduced:
 (2)
(2)
These are used to define pseudoimpedance, and pseudodistance:
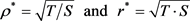 (3)
(3)
as well as pseudoanisotropy coefficient
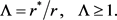 (4)
(4)
The bound for Λ is known in mathematical geophysics [5] . For further use the contraction coefficient is introduced
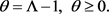 (5)
(5)
These way the medium is reparametrized into pseudoimpedance varying in only one pseudodirection,
.
Cyclic, and pseudohomogeneous medium. When proper impedance of a medium is varying between high and low values, in a direction r, such medium is said to be repetitious, or cyclic. The media, cyclic in all directions could be considered but we refer to 1D space as investigated in geophysical theory.
Typical distance between successive local extrema of impedance is of order denoted as ∆r. Consider a medium which is cyclic in a microscale (typical distance ∆r), and when
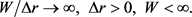 (6)
(6)
For global seeing, in macroscale the space metrized as
is applied. The medium appearing in a macroscale is said to be isotropic and pseudohomogeneous if the resulting both pseudoimpedance and contraction coefficient reveal as directionless and constant over a macrospace. As known in geophysical prospecting, the locally alternating parameter exhibits globally the quasi-homogenity while distance is stretched by pseudoanisotropy coefficient, Λ.
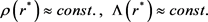 (7)
(7)
2.1. Doppler-Like Effect
In conformity with scale relationship, Equation (4), the scale for homogeneous medium is stretched by a factor Λ when passing to pseudohomogeneous medium. The effect of contraction is well known in direct current resistivity sounding over horizontally stratified earth [11] [12] , where Λ is termed as pseudoanisotropy coefficient. For horizontally stratified media (proper impedance varying in z-direction only), the governing Equation (1) takes the form
(8)
when asterix refers to alternative as to homogeneity of a medium. The options
(inhomogeneous medium), or
(pseudohomogeneous medium) yield different depth of a layer. Eventually, but it is not the practice, the horizontal scales are to be contracted, yielding
, and
.
Doppler-likeness of this effect consists in the following. For 3-D pseudohomogeneous medium, we have
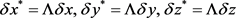 (9)
(9)
and substitution ω* = Λω is possible in the governing Equation (1), then becoming
(10)
Now anomalous wave frequency ω* may take interpretation either in a fine scale of heterogeneities, Equation (1), or in a coarser scale of regional investigation, Equation (11). Thus contraction coefficient, θ, appears as a static counterpart of Doppler shift, as detailed further on.
Relative to the expansion, the governing equation could be read
(11)
2.2. Superimposing Scales
In DC geosounding, there is a stock-still layering and so is the varying frequency models. Suppose, with no à priori knowledge about homogenity, the measurements taken on earth surface indicates the depth H, or h for homogeneous, or heterogeneos layers, respectively. Thus, further examination (drilling) is performed, in practice. The final assignment is made depending on the ratio H/r. The resulting correction is attributed to different metric properties of homogeceous and heterogeneous layering. The effect is referred to as superimposition of scales. This way (by drilling), the homogenity-heterogenity self-entanglement becomes unraveled in the case.
What is a principal difference between superimposition and superposition methods like additive color, or substractive color methods, or else a moiré pattern? Physical manifestation of a superposition is frequently the interference whereas the superimposition consists in medium identification in a communication channel, used to convey information, or energy throughout. This could be the physical transmission media, or a multiplexed medium in a logical connection. Possibly, the Laplacian mirror window [13] should be more comprehensive in answering the question.
3. Discussion: Expansion or Heterogeneities?
Equivalence, or analogy in mathematical description of physical phenomena in time, frequency, and space is well known [4] . Quite naturally, the Doppler shift can be due not only to movement of the source or expansion of space but also to greater travel time owed to inhomogeneities.
Introducing Equation (5) into (4) yields
(12)
which in static systems is quantified by
distance correction = contraction coefficient ・ simple distance.
When the time is introduced to reach kinematical systems, the shift related to equation (11) is quantified by
with
coeff. = (observed wavelength ? emitted wanelength)/emitted wavelength.
Similarly, relative to the expanding universe, the expansion rate related to equation (12) is quantified by
receding velocity of a galaxy = Hubble constant ・ current distant to the galaxy.
Note that contraction coefficient is dimensionless quantity whereas Hubble constant is dimensioned in t−1.
The energy propagating in inhomogeneous universe exhibits a shift which could be attributed not only to the expansion of space but alternatively to fluctuations in material properties (inhomogeneities). When nothing is known about kinematics of a system’s structure, both causes might share in the effect.
An Example
Let us consider an example of 1D space divided between large segments, rv, with void occupancy individualized with proper impedance ρv, and small segments, rp, with particle occupancy individualized with proper impedance ρp. The large and small segments interleave and value of 1032 is assumed for the ratio rv/rp. In the 1D universe of such sparsely distributed particles, a very high impedance’s contrast is to be assigned for contraction coefficient to match high absolute values (up to the Hubble’s constant in the expanding universe).
On the other hand, when there is a number of scales, in hierarchical sequence, the effects of subsequent reparemetrizations are multiplied [5] . Let us take into investigation a mega-region of size much larger than macro-region W. Let the same relations are settled between mega- and macro-scales, as it was for macro- and micro-scales. The outcoming pseudoanisotropy coefficient is obtained as a product of coefficients graded by the size of corresponding subregions. Effective Doppler-like shift is increasing with the size of a region under investigation.
4. Conclusions
・ The affirmative answer to the introductory question opens different static as well as kinematic possibilities, which challenge established theories of expanding universe and energizing big bang. First step in such prospects was made quite recently [14] putting geophysical theory and Hubble’s law in parallel. Stock-still system―a void with sparsely distributed particles―stands up as a scenario for propagation of electromagnetic waves accompanied with Doppler-like effect along with a Hubble-like law.
・ The distance contraction, as observed in electrical soundings over horizontally stratified earth (static system), is identified as a counterpart of Doppler shift in dynamical systems. An alternative answer to the question about an effective cause of the Doppler shift sounds the heterogeneities under superimposing scales.
・ Otherwise, the theory is indicative for new technologies in energy transmitting materials or information (communication) channels: layering, material profile, vocal tract are to be adequately structured. The application of augmented or/and extended reality to support understanding of the cognitive processes was helpful in establishing a steady progress in the research of electrical impedance tomography (EIT), leading to important developments. “These developments have excited interest in practitioners and researchers from a broad range of disciplines, including mathematicians devoted to uniqueness proofs and inverse problems, physicists dealing with bioimpedance, electronic engineerers involved in developing and extending its applications, and clinicians wishing to take advantage of this powerful new imaging method” [15] .
・ At sub-atomic level there is the Raman spectroscopy dealing with the scattering of light with no its absorption [16] . The resulting Raman shift [17] provides a fingerprint to identify molecules and has a wide variety of applications in biology and medicine, and others [18] . This microscale effect has to be seen in parallel with the macroscale Doppler Effect.