Identifying a Kaluza Klein Treatment of a Graviton Permitting a Deceleration Parameter q(z) as an Alternative to Standard DE ()
1. Introduction
The idea behind this article has been to investigate how a speed up of cosmological expansion could occur, i.e. involving the de celeration parameter as defined below [1] is a way to look for a mechanism to explain how a speed up of expansion is possible. Settling upon the lowly graviton is done, since if the graviton has a very slight rest mass in four dimensions, we have a way to unify both dark matter and dark energy expressions [1] [2] .
What is done is to have the mass of the graviton equal to a dark matter expression plus a contributing factor dark energy contribution. Having a very light, but non zero rest mass to the rest mass of the graviton in four dimensions corresponds to dark energy. As we have considerable cosmological expansion history to traverse before one billion years ago, with a slow decrease of the rate of de celebration of the expansion of the universe, it is fitting that the ultra light rest mass of the graviton at red shift value of z = 0.423, i.e. one billion years ago, eventually contributes to a speed up of cosmological expansion.
Secondly, afterwards, we consider what sort of signal contribution we could identify would allow identifying GW generation as connected with massive gravitons. Actual hardware requirements which may enable such a quest are in reference [3] .
The analogy with axions is picked in part, with a nod to solar axion research, as to help researchers identify signal pick up regimes of massive gravitons which could be picked up by appropriate GW/graviton detector technology [3] . Furthermore, the expectation is that the rate of graviton detection and also of GW detection would be in a comparatively narrow band of frequencies, and that it is unlikely that there would be a smooth curve of rates of production of “particles” or events detected, which is the expected result in terms of axions. The hope is that eventually if we can detect gravitons that confirmation of their effective mass will lead to partial experimental confirmation as to the idea that the graviton is indeed part of re acceleration of the universe one billion years ago. Doing so will be, in the end equivalent of the datum that an effective “current” of “massive” gravitons, as will be referred to at the end of this document in the discussions section. The effective “current” of “massive” gravitons as contributing to re acceleration of the universe, if confirmed would have many exciting cosmological implications and would help to create experimentally falsifiable conditions for the birth of GW astronomy. The main point of what the “massive” graviton current permits physically is in the “discussions” section of this document.
2. Basic Theme, How to Identify the “Foot Print” of “Massive” Gravitons
This article begins by a question of how to identify a Kaluza Klein treatment of a graviton in five dimensions, with a DM component and a very small rest mass in four dimensions, similar to the behavior of DE a billion years ago. After a grounding in gravitational wave density, the issue of a rate equation for production of relic particles from initial cosmology will be proposed as a research goal. The analogy of DM from axions from the Sun having a rate equation graph plotted against frequency is suggested as a worthy goal of researchers if Kaluza Klein gravitons can be detected and measured. However, production of axions from the Sun is broadband whereas in most likelihood, the relic particle production of gravitons would be in narrow frequency ranges. as predicted by Grishchuk [4] Gravitational wave density will be presented as necessary background.
We will start with a first-principle introduction to determination of gravitational wave energy density
using the definition given by Maggiore [5]
is defined as a way to measure gravitational wave strength as a function of general random energy fluctuation backgrounds. Equation (1) measures the strength of the gravitational wave signal.
 (1)
(1)
where
is the frequency-based numerical count of gravitons per unit phase space. Since
is usually an extremely small fraction of very noisy relic cosmological background conditions, the representation of
is based on scaling its relative strength. i.e., Figure 1 shows the magnitude of
for different cosmological models. Here,
is the same as
as of Figure 1 below. Combining experimental confirmation of Equation (1) with
observations using different values of 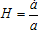 and
and  will be tied in with analysis of the plots in Figure 1. Note, these models as not consistent with each other.
will be tied in with analysis of the plots in Figure 1. Note, these models as not consistent with each other.
Grishchuk [7] states the relation between
(which he refers to as
) and the frequency spectrum
as given in Equation (2). The models brought up in Figure 1 need to be compared with each other, as part of experimental inquiry.
![]()
Figure 1. Abbott et al. [6] (2009) shows the relation between GW frequency and GW energy density for different cosmological models.
Equations (2) and (3) are part of that comparison.
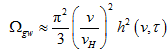 (2)
(2)
We will address the divergences between models presented by Maggiore, Abott, and Grishchuk and will develop candidate discriminating criteria for a number count
based on Glinka’s [8] graviton gas work:
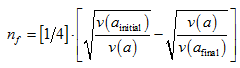 (3)
(3)
If
 (4)
(4)
If we assume
, and substituting Glinka’s [8] approximation of a graviton “gas” by treating gravitons as boson “particles” in the early universe― permitting a rapid accumulation of “gravitons” in the initial phase of the big bang―then for very high
values, Equation (3) will in most cases be approximately,
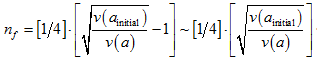 (5)
(5)
Frequently, a researcher will be looking at
, and comparing that value with what one gets for Equation (5) with
in pre-big-bang scenarios, with initial values of frequency set for
Hz, as specified by Grishchuk [4] . Notice that
Hz near the present era. Table 1, Table 2, and Table 3 are based on Equations (4) and (5), as to forming a suitable counting algorithm. The idea is to use a semi-classical approximation via the Wheeler De Witt equation as described by Glinka [8] for early-universe gravitons. This semiclassical approximation, by treating gravitons
![]()
Table 1. If one assumes
.
![]()
Table 2. If one assumes
.
![]()
Table 3. If one assumes
.
as bosons, will permit up to 106 particles as entropy units being manufactured within Planck length values of space-time volume, i.e., roughly 10120 times smaller
As will be explained in the Appendix, there is a way to relate graviton count and entropy, so then the numbers associated with
are a de facto counting algorithm for entropy per unit phase space. Note that the highest counting numbers for entropy are associated with
, which, according to Figure 1, is associated with pre-big-bang GW/graviton production.
is associated with usual inflation, as given in Figure 1. i.e., if one is looking for standard creation of entropy paradigms associated with the early universe, a typical phase transition argument for early entropy production is given by Tawfik [9] (2008), which for QCD regimes is shown in Equation (6).
(6)
where S = entropy. We assume here that
may be associated with gravitons/GW at the very end of inflation, and not the beginning (where one would have a far lower initial count, i.e., S ~ 107) and with frequencies initially on the order of 108 to 1010 in the beginning of cosmological evolution. Such a huge burst of graviton production for temperatures on the order of
would lead to measurable consequences.
3. Gravitons with a Non Zero Rest Mass. The KK Treatment
Consider if there is then also a small graviton mass, i.e., as stated by Beckwith [1] [2] :
(7)
Note that Rubakov (2002) works with KK gravitons, without the tiny mass term for a 4 dimensional rest mass included in Equation (7). To obtain the KK graviton/DM candidate representation along RS dS brane world, Rubakov obtains his values for graviton mass and graviton physical states in space-time after
using the following normalization:
. Rubakov [10] (2002) uses
which are different forms of Bessel functions.
His representation of a graviton state is given by Equation (8), which is almost completely acceptable for our problem, since the rest mass of a graviton in four dimensions is so small. If so, then the wave function for a graviton with a tiny 4 dimensional space time rest mass can be written as [10] .
(8)
Equation (8) is for KK gravitons having a TeV magnitude mass
(i.e., for mass values at 0.5 TeV to above 1 TeV) on a negative tension RS brane. It would be useful to relate this KK graviton, which is moving with a speed proportional to
with regards to the negative tension brane with
as an initial starting value for the KK graviton mass. If Equation (8) is for a “massive” graviton with a small 4 dimensional gravition rest mass and if
represents an initial state, then
one may relate the mass of the KK graviton moving at high speed with the initial rest mass of the graviton. This rest mass of a graviton is
, opposed to
. Whatever the range of the graviton mass, it may be a way to make sense of what was presented by Dubovsky et al. [11] , who argue for a graviton mass, using CMBR measurements, of
. Also, Equation (9) will be the starting point used for a KK tower version of Equation (9). So from Maartens [12] ,
(9)
Maartens [12] also gives a 2nd Friedman equation:.
(10)
Also, an observer is in the low redshift regime for cosmology, for which
, for red-shift values z from zero to 1.0 - 1.5. One obtains exact equality,
, for z between zero to 0.5. The net effect will be to obtain, based on Equation (10), assuming
and using
to get a deceleration parameter q as given in Equation (11).
(11)
These set values, along with a revised Equation (10) allow a graviton-based substitute for DE.
plus a small rest mass for a graviton in four dimensions allows for “massive gravitons” that behave the same as DE. Setting
, while having a modified behavior for the density expression, for a Friedman equation with small 4 dimensional graviton mass, means that dark energy is being replaced by a small 4 dimensional rest mass for a graviton.
4. Consequences of Small Graviton Mass for Reacceleration of the Universe
In a revision of Alves et al. [13] , Beckwith [1] [2] used a higher-dimensional model of the brane world combined with KK graviton towers per Maartens [12] . The energy density
of the brane world in the Friedman equation is used in a form similar to Alves et al. [13] by Beckwith [1] [2] for a non-zero graviton:
(12)
Beckwith [6] [7] suggests that at z ~ 4, a billion years ago, acceleration of the universe increased, as shown in Figure 1. Figure 1 is, if confirmed a good verification of the Ng [12] hypothesis, and would be a starting point to investigate the role of gravitons in cosmology. The author notes that Buonnano [13] assumes a much lower range of initial frequencies for relic GW than the author. Beckwith [6] , [7] obtained a re-acceleration of the universe result as given in Figure 2. The contribution of a low rest mass for 4 dimensional gravitons, as given in Equation (7) leads to a speed-up of acceleration of the expansion of the universe a billion years ago, i.e. for a red shift slightly smaller than 0.5. Figure 2 below is predicated upon a small 4 dimensional rest mass (stated in Equation (7) for a graviton behaving the same as dark energy)... We will state in our discussions section as to what is needed to give experimental confirmation as to what is a current for a “massive” graviton which is appropriate for explaining in part, Figure 2 below.
5. Comparison with Axion Flux Results from the Sun: What Would be Needed to Measure Dm Flux for a New Model of Dm/De?
This section is intended to explain a rate of particle production as given for solar axions, and to determine what may be necessary to adapt such an approach for
![]()
Figure 2. Re-acceleration of the universe based on Beckwith [1] ; (note that q(z) < 0 if z < 0.423).
Kaluza-Klein gravitons in the onset of inflation. Figure 3 is a redo by the author, using the Dimpoulou et al. [16] value of axion flux, while noting that it is similar to the axion flux from the sun, per Lazaruth et al. [17] . It would be appropriate to do the same with the DM implied by Equation (7). Figure 3 is based on Equation (13), given by Buoanno [15] , for applied frequency
vs.
, axion flow in KeV values of solar axions:
(13)
Equation (13) models what happens for axions in the sun, and we hope to eventually obtain a similar rate expression of graviton production for Kaluza Klein gravitons as given in Equation (7) versus energy, similar to what is shown in Figure 3, in the case of solar axions.
The rate of production of solar axions
is plotted against frequency,
. Beckwith’s goal is to eventually duplicate Figure 3 for relic gravitons, using data collection for Kaluza-Klein gravitons. This rate equation plotted in Figure 3, as given in Equation (13) as used by Beckwith, is dominated by
(
a plasma interaction effect that is to be determined, and
is part of the expression for permitted solar axion energy values.
in most cases. The author suggests finding grounds for a similar energy plot of DM values from a suitably modified version of Equation (7) for KK dark-matter candidates. Doing so would mean understanding how a rate equation based upon Equation (13) for DM production could commence using a model of KK DM production/evolution. The author suggests that it would be appropriate to use an early universe counterpart to the known model of axion production in stars to illustrate the correspondence of axion production in the sun with relic particle production in the early universe. For Equation (14),
the number density of Z atoms with an ionized K shell,
the number density of free electrons,
a general density of states for the axion-producing background, and
the axio-recombination (free-bound) cross-section is given by Dimopoulous [16] . However, this leaves open the question of whether the cross section
for the LHC values of massive gravitonsis similar to what is done in stars. The usual assumption is that the
![]()
Figure 3. Beckwith’s revision of axion flux from the Sun, in terms of (frequency=energy, if
), with the plot of the nmber of axions produced by the Sun in terms of KeV values of solar axions.
definitions correspond. Equation (14) is a rate of production of axions.
(14)
Equation (14) has corresponds partially with Equation (13), but differs due to the density value
, which may be derived experimentally. In the early universe, for a KK dark matter counterpart, we would still have a density value
to consider and a possible
for cross section for some interaction of KK DM production. However, due to early universe conditions, there would be no counterpart to
or
. Durrer, Marozzi , and Rinaldi [18] have used very early universe plasmas, going back to the electroweak transition and turbulence, as a model for early-universe GW production. One would need to specify how to obtain
for some interaction of KK DM production, which is why observation of the mass and width (or cross section) of one or more KK gravitons, as part of a DM candidate, at the LHC, as remarked by Grzadkowski et al. [19] may be the only way to obtain experimental inputs into a graviton production/KK DM version of Equation (14). However, this leaves open the question of whether the cross section
for the LHC values of massive gravitons, etc, would be the same as what would occur for early universe conditions. So far, the only known theoretical calculations of the above are along the lines of
arising from photon and neutrino annihilation rates, as given by Hewett [20] . The author is attempting to obtain suitable values of
to put in the given calculation at the start of the inflationary era.
6. Findings, Discussion of Results
We can use Figure 3 as an idea of how to identify rate ofgraviton collection opportunities against frequency for a detector along the lines of reference given in reference [3] . What is expected though is that instead of the smoothly varying curve that if gravitons were matched against rates, in a similar manner, that there would be spikes, instead of smooth variations. Once GW astronomy becomes a fact, Figure 3 for gravitons will emerge. The sharpness of the spikes, if analyzed properly will say much about the supposition given in Equation (7) about a KK decomposition of the mass of a graviton into dark matter and dark energy contributions.
What is most intriguing, is the possibility of Equation (11) having a non uniform frontier of re acceleration of the universe, a billion years ago. Not a “perfect sphere” of re acceleration, but one with a jagged edge of moving space time regions. i.e. a complicated structure. In part, adding more details to supposed “cosmic voids” and regions of space time distrutions of galaxies in, say, a fractal geometric manner, as given in reference [21] . If and when GW astronomy becomes a fact, suppositions as to how galaxies are distributed through space time may obtain a phenomenological descriptive rationale, which we hope leads to falsifiable experimental measurements. [22] . The main point we wish to emphasize is that to do all of this, the following current behavior in a GW/graviton detector would have to be verified for massive gravitons. This is the geometry of space time which may be confirmed by appropriate analysis of Equation (11). So, next, how to confirm the reality in falsifiable experimental conditions for obtaining “massive” gravitons making all of this possible?
What Li et al. have shown in 2003 [23] which Beckwith commented upon and made an extension in [24] is to obtain a way to present first order perturbative
electromagnetic power flux, i.e. what was called
in terms of a non zero four
dimensional graviton rest mass, in a detector, in the presence of uniform magnetic field, when examining the following situation, i.e. [23] what if we have curved space time with say an energy momentum tensor of the electromagnetic fields in GW fields as given by
(15)
Li et al. [23] state that
, with
will lead to
(16)
The 1st term to the right hand side of Equation (16) is the energy ? momentum tensor of the back ground electromagnetic field, and the 2nd term to the right hand side of Equation (16) is the first order perturbation of an electromagnetic field due to the presence of gravitational waves. The above Equation (15) and Equation (16) will eventually lead to a curved space version of the Maxwell equation. As was given in [23]
(17)
as well as
(18)
Eventually, with GW affecting the above two equations, we have a way to isolate
. If one looks at if a four dimensional graviton with a very small rest mass included [24] we can write
(19)
where for
but very small
(20)
The claim which A. Beckwith made [24] is that
(21)
As stated by Beckwith, in [24]
, while
is the number of gravitons which may be in the detector sample. What researchers
intend to do is to try to isolate out an appropriate
assuming a non zero
graviton rest mass. This if successfully done would be enough to help obtain some experimental confirmation as to Figure 2, as well as give more understanding as to the physics inherent as to Figure 3, in its GW/graviton physics configuration. The hope is that proving Equation (21) above will lead to falsifiable experimental results as to many topics in cosmology which so far are a province of many disparate cosmology models. A situation we hope to rectify in the 21 century.
7. Conclusions
Can GW/Gravitons do double duty as DM/DE candidates in cosmic evolution? Beckwith [1] [2] investigated whether gravitons could be a graviton gas as a substitute for a vacuum energy. He also considered a suggestion by Yurov [25] of double inflation, which if verified would support the models in Figure 1. What is to be done is to obtain a rate of production of KK relic gravitons over a frequency range different from that of axions from the Sun, as done in Figure 3. Assuming gravitons as a bosonic gas permits up to a million gravitons in a volume of space 10120 smaller than what is normally predicted. Eventually, deriving a new rate of graviton production for early universe conditions will be necessary, and the author expects that it will be over a far narrower range of frequencies than given in Figure 3. This is what we will investigate [3] . We are also intrigued by the possibility that as given in [21] that proper analysis of Equation (7) via instrumentation [22] will allow us to understand the space time geometry of galaxy clusters, and of the density of space time just at the point of re acceleration of the universe a billion years ago. To do this, we should attempt to, if a detector can be built with a uniform magnetic field which may allow us to identify and confirm a current from “ massive “ gravitons equivalent to Equation (21). We also state that confirmation of Equation (21) would give credence to a unified DM/DE model as an alternative to the Claperyon Gas models [26] which have been discussed time and time again. Finally, it also would give an insight as to additional dimensions which may be revealed by gravitational wave astronomy [27] which so far has been a theoretical enterprise with no experimental input so far.
Here is a thought for future reference, i.e. what is known is that [28] by LIGO is given in the following quote:
We bound the graviton mass to m(graviton) ≤ 7.7 × 10−23 eV/c2. In all cases, we find that GW 170104 is consistent with general relativity.
End of quote
The significance of this is two-fold, i.e. it affects the value of Equation (21) and secondly, if the presumed current is tied into, with modifications, an affirmation of the existence of early universe magnetic fields, then the bound on the mass of a graviton is of crucial importance.
In addition, we have that [29] is also in play, with the results that Christian’s observations as to the tests for general relativity have to be confirmed, and reviewed. Our bound on the graviton and the observation as to [28] as to the consistency of the binary black hole connectivity to General relativity has to be balanced with the scalar-tensor models brought up by Christian Corda in [28] .
Both [28] and [29] affirm the importance of gravitational wave astronomy to foundational investigations of general relativity.
Fund
This work is supported in part by National Nature Science Foundation of China grant No. 11375279.
Nomenclature
= partition function, a concept usually from statistical physics.
= frequency of a space plasma.
= number density, i.e., the numerical count for Z atoms in a phase-space regime.
= wavelength of a “particle.” (wave-particle duality of quantum mechanics).
= cross section, in QM, usually in units of
times spatial distances, squared.
z = redshift =
, where v is the speed of a “particle” and c is speed of light.
= density of “physical states,” i.e., usually associated with physical states in a unit of phase space “volume.”
KK. = Kaluza-Klein. A model that seeks to unify the two fundamental forces of gravitation and electromagnetism In the case of this paper, it is for particles obeying a unification of gravitation and electromagnetism.
is a “deceleration” parameter; when positive, it means cosmic acceleration is slowing down, and when negative, it means cosmic acceleration is speeding up.
a = scale factor, and the dots refer to time derivatives.
= rest mass of a graviton. Usually in four dimensions: ~ 10?65 grams
= Gravitational wave density, rescaled, with
and
, critical density. Here,
is a ration of the relative strength of a gravitational wave over a general energy background observed in cosmology.
P = pressure. i.e.,
, with regards to density and pressure.
K = curvature, i.e,. K = 0 means zero space-time curvature (flat space).
DM = Dark Matter.
DE = Dark energy.
Appendix
The appendix section presents how a modification of infinite quantum statistics by Ng [14] permits a one-to-one identification of entropy with relic “particle” production in the early universe. This step by Ng [14] uses a small graviton creation volume, V; for high frequency (short wavelength) relic gravitons right after the big bang. What follows is consistent with Ng [14] if the graviton volume V for nucleation is tiny, well inside inflation values. So the log factor drops out of entropy S if V as an initial space-time volume is chosen properly for both equation 1 and
(1)
Ng’s [14] result begins with modification of the entropy/partition function that Ng used in an approximation of temperature, starting with early temperature
(
represents the region of space of the particles in question).
Equation (15), according to Ng, leads to entropy of the limiting value of a counting algorithm,
will be modified by what Ng [14] refers as using infinite quantum statistics, as given in Equation (2).
(2)
Furthermore, assume that the volume of space is of the form
and look at a numerical factor
, where the denominator is Planck’s length (on the order of 10−35 centimeters). We also specify a “wavelength”
. So the value of
and of
are the same order of magnitude. Note Ng (2008) changed conventional statistics: he outlined how to get
or
(where
is graviton density), begining with a partition function as written in Equation (1).