1.Introduction
In paper [1] ,the author studies the problem whether 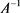 is the generator of a bounded C0-semigroup if A generates a bounded C0-semigroup.We know that α-times resolvent operator family is generalization of C0-semigroup and C0-semigroup is 1-times resolvent operator family.So,in this paper,we will show that when the operator
is the generator of a bounded C0-semigroup if A generates a bounded C0-semigroup.We know that α-times resolvent operator family is generalization of C0-semigroup and C0-semigroup is 1-times resolvent operator family.So,in this paper,we will show that when the operator 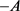 generates a bounded α-times resolvent operator family,under certain condition,
generates a bounded α-times resolvent operator family,under certain condition,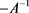 is also the generator of a bounded α-times resolvent operator family.The representation of such bounded α-times resolvent operator family will be obtained,too.Furthermore,we will consider the problem whether
is also the generator of a bounded α-times resolvent operator family.The representation of such bounded α-times resolvent operator family will be obtained,too.Furthermore,we will consider the problem whether  owns this property.
owns this property.
Let us first recall the definitions of α-times resolvent operator family.Let A be a closed densely defined linear operator on a Banach space X and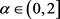 .
. is a Mittag-Leffler function.
is a Mittag-Leffler function.
Definition 1.1 [2] A family 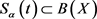 is called an α-times resolvent operator family for A if the following conditions are satisfied:
is called an α-times resolvent operator family for A if the following conditions are satisfied:
1)  is strongly continuous for
is strongly continuous for 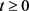 and
and ;
;
2) 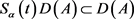 and
and 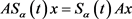 for
for  and
and 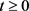 ;
;
3) For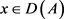 ,
,![]() satisfies
satisfies
![]()
where![]() ,
,![]() .
.
If ![]() where
where![]() ,we write as
,we write as ![]() (or shortly
(or shortly![]() ).Then we give the definitions of analytic α-times resolvent operator family.
).Then we give the definitions of analytic α-times resolvent operator family.
Definition 1.2 [2] An α-times resolvent family ![]() is called analytic if
is called analytic if ![]() admits an analytic extension to a sector
admits an analytic extension to a sector ![]() for some
for some![]() ,where
,where![]() .An analytic solution operator is said to be of analyticity type
.An analytic solution operator is said to be of analyticity type ![]() if for each
if for each ![]() and
and![]() ,there is
,there is ![]() such that
such that![]() .
.
Then we give a Lemma which will be used later.
Lemma 1.1 [2] ![]() .Then
.Then ![]() if and only if
if and only if ![]() and there is a strongly continuous operator-valued function
and there is a strongly continuous operator-valued function ![]() satisfying
satisfying![]() ,and such that
,and such that
![]()
2.Main Theorem and Conclusion
Theorem 2.1.On a Hilbert space H,the following statements are equivalent:
(1)![]() ,
,![]() ;
;
(2) A is a closed,densely defined operator,![]() ,and for
,and for![]() ,
,![]() ;
;
(3) A is a closed,densely defined operator,for![]() ,
,![]() and
and ![]() is invertible for some
is invertible for some![]() .
.
Proof.(2) Þ (3) For![]() ,
,![]() ,then we have for
,then we have for![]() ,
,
![]() (1)
(1)
hence we know ![]() is invertible from the proposition 1.5 of chapter 3 in book [3] .While,from equation (1),we can also have for
is invertible from the proposition 1.5 of chapter 3 in book [3] .While,from equation (1),we can also have for![]() ,
,![]() ,then
,then![]() .
.
(3) Þ (2) Since![]() ,
,![]() ,then for
,then for![]() ,
,![]() .
.![]() is invertible for some
is invertible for some ![]() imply that
imply that ![]() is invertible for any
is invertible for any![]() .Together with A is closed and densely defined,we have
.Together with A is closed and densely defined,we have![]() ,hence
,hence![]() and
and ![]() .
.
(1) Þ (2) From lemma 1.3 of [4] ,we know that A is a closed,densely defined operator.And we can get the other conclusion from theorem 2.8 of [2] .
(2) Þ (1).Firstly,set![]() .For every
.For every![]() ,
,![]() is a bounded operator and can commute with one another.It follows from Theorem 2.5 of [2] that
is a bounded operator and can commute with one another.It follows from Theorem 2.5 of [2] that ![]() generates an α-times resolvent family
generates an α-times resolvent family ![]() which is also uniformly continuous and exponential bounded.
which is also uniformly continuous and exponential bounded.
For![]() ,
,![]() .There exists a
.There exists a![]() ,such that
,such that![]() ,that is
,that is![]() .Then
.Then
![]()
Since ![]() and
and![]() ,then we have that
,then we have that![]() .It means that for
.It means that for![]() ,
,![]() .Consequently,
.Consequently,![]() ,and
,and![]() .
.
From Lemma II,3.4(ii) of [5] ,we have that ![]() converges to A pointwise on
converges to A pointwise on![]() .If we can get the following properties,we will have
.If we can get the following properties,we will have![]() .
.
(a) ![]() (*) exists for
(*) exists for![]() ;
;
(b) ![]() is an α-times resolvent family which is generated by A;
is an α-times resolvent family which is generated by A;
(c)![]() .
.
(a) For ![]() is bounded,we can only need to prove (*) on
is bounded,we can only need to prove (*) on![]() .For
.For![]() ,
,
![]()
where ![]() ((2.52) and (2.53) of [2] ).Together with
((2.52) and (2.53) of [2] ).Together with![]() ,we can get that
,we can get that![]() .Thus for
.Thus for![]() ,
,
![]()
By Lemma II,3.4(ii) of [5] ,![]() is a Cauchy sequence for each
is a Cauchy sequence for each![]() .Therefore
.Therefore ![]() converges uniformly on each interval
converges uniformly on each interval![]() .
.
(b) I.For![]() ,
,![]() is the uniformly continuous functions and so is continuous itself.For each
is the uniformly continuous functions and so is continuous itself.For each![]() ,
,![]() is uniformly bounded on every interval
is uniformly bounded on every interval ![]() and
and![]() ,then so is
,then so is![]() .By Lemma I,5.2 of [5] ,
.By Lemma I,5.2 of [5] ,![]() is strongly continuous and
is strongly continuous and![]() .
.
II.For![]() ,
,![]() ,
,![]() and
and![]() .Together with that A is an closed operator,we have that
.Together with that A is an closed operator,we have that![]() .That is
.That is![]() .
.
We have![]() ,
,![]() and
and ![]() converge to A and
converge to A and ![]() pointwise,respectively.So,we have
pointwise,respectively.So,we have![]() .
.
III.We know that
![]()
And for![]() ,
,![]() converges uniformly on the interval
converges uniformly on the interval![]() ,then
,then
![]()
For all the above,we can obtain that ![]() is an α-times resolvent family which is generated by A.
is an α-times resolvent family which is generated by A.
(c) For each![]() ,
,![]() and
and ![]() converges to
converges to ![]() pointwise,so
pointwise,so![]() ,too.That is
,too.That is![]() .
.
To sum up the above (a),(b) and (c),we can conclude that![]() .
.
Theorem 2.2.![]() ,
,![]() Û A is a closed,densely defined operator,
Û A is a closed,densely defined operator,![]() ,and for
,and for![]() ,
,![]() .
.
Proof.In the proof of the previous theorem,we have only used the properties of Hilbert space in the acquisition of ![]() and we can get
and we can get ![]() without the properties of Hilbert space.
without the properties of Hilbert space.
In fact,on a Banach space,for each![]() ,
,![]() can generate a C0-semigroup
can generate a C0-semigroup![]() .Moreover,
.Moreover,
![]()
From the subordination principle,we have![]() ,where
,where![]() .So
.So
![]()
We can obtain that this theorem is tenable from the proof of the previous theorem.
Theorem 2.3.On a Hilbert space H,if![]() ,
,![]() and
and ![]() exists as a closed,densely defined operator,then
exists as a closed,densely defined operator,then![]() .
.
Proof.From the above Theorem 2.1,we have![]() ,and for
,and for![]() ,
,![]() .And
.And ![]() exists as a closed,densely defined operator,so it is easy to show that
exists as a closed,densely defined operator,so it is easy to show that ![]() is bounded invertible for some
is bounded invertible for some![]() ,from (8) of [1] .Further more,for
,from (8) of [1] .Further more,for![]() ,then
,then![]() ,thus there exists an
,thus there exists an![]() ,such that
,such that![]() .Then
.Then ![]() .By Theorem 2.1,we can obtain that
.By Theorem 2.1,we can obtain that![]() .
.
Theorem 2.4.If![]() ,
,![]() ,
,![]() is the α-times resolvent family generated by it and
is the α-times resolvent family generated by it and![]() .And if
.And if ![]() exists as a closed,densely defined operator,then
exists as a closed,densely defined operator,then ![]() generates an α-times resolvent family
generates an α-times resolvent family![]() ,which is given by
,which is given by
![]()
where ![]() is the first order Bessel function [6] .Moreover,there exists an
is the first order Bessel function [6] .Moreover,there exists an![]() ,such that
,such that![]() .
.
Proof.Since![]() ,then
,then![]() .Together with the assumption that
.Together with the assumption that ![]() is a closed,densely defined operator,we have that
is a closed,densely defined operator,we have that![]() .Because of the property of Bessel function
.Because of the property of Bessel function ![]() and for large t,
and for large t,![]() ,then
,then
![]()
Thus,the integral is well defined.Set ![]() .Obviously,
.Obviously,![]() is strongly continuous and
is strongly continuous and![]() .From the above discussion,we can get that
.From the above discussion,we can get that![]() .For
.For![]() ,
,
![]()
Consequently,we can obtain a conclusion that ![]() generates an α-times resolvent family
generates an α-times resolvent family ![]() from Lemma 2.1 and
from Lemma 2.1 and ![]() ,
,![]() .
.
Theorem 2.5.A satisfies the assumption of Theorem 2.4,for![]() ,
,![]() generates a bounded analytic α-times resolvent family
generates a bounded analytic α-times resolvent family![]() .If
.If![]() ,then
,then
![]()
where
![]()
and
![]()
is oriented counterclockwise,where
![]()
![]()
![]()
and![]() .
.
Proof.![]() ,so
,so ![]() and
and![]() .For
.For![]() ,
,![]() .It follows from the Remark 2.8(a) of [7] that
.It follows from the Remark 2.8(a) of [7] that ![]() generates a bounded analytic α-times resolvent family
generates a bounded analytic α-times resolvent family![]() .If
.If![]() ,we set
,we set
![]()
Since![]() ,then
,then
![]()
From [8] ,we have that there exists an![]() ,such that
,such that![]() .Next we estimate
.Next we estimate![]() ,it follows from (2.4) of [8] that
,it follows from (2.4) of [8] that
![]()
![]()
The same estimate holds for the integral on![]() .
.
![]()
The same estimate holds for the integral on![]() .
.
![]()
To sum up,we can conclude that there exists an![]() ,such that
,such that![]() .So
.So![]() .Then we should show that
.Then we should show that ![]() is strongly continuous at 0.It following from the dominated convergence Theorem and Fubini Theorem that
is strongly continuous at 0.It following from the dominated convergence Theorem and Fubini Theorem that
![]()
For![]() ,it follows from Fubini Theorem that
,it follows from Fubini Theorem that
![]()
From all the above,we can obtain a conclusion that if![]() ,
,![]() generates a bounded analytic α-times resolvent family
generates a bounded analytic α-times resolvent family![]() ,
,
![]()
3.Conclusion
In this paper,we considered when the operator ![]() generates a bounded α-times resolvent operator family,under certain condition,
generates a bounded α-times resolvent operator family,under certain condition,![]() as well as
as well as ![]() is also the generator of a bounded α-times resolvent operator family.Through the study of the problem whether
is also the generator of a bounded α-times resolvent operator family.Through the study of the problem whether ![]() is the generator of a bounded α-times resolvent operator family if A generates a bounded α-times resolvent operator family,we can know the generator A more clearly.Furthermore,this work can improve the study of the inverse problem.
is the generator of a bounded α-times resolvent operator family if A generates a bounded α-times resolvent operator family,we can know the generator A more clearly.Furthermore,this work can improve the study of the inverse problem.
Acknowledgements
The author was supported by Scientific Research Starting Foundation of Chengdu University,No.2081915055.