Why Flat Space Cosmology Is Superior to Standard Inflationary Cosmology ()
1. Introduction and Background
The Boomerang, Wilkinson Microwave Anisotropy Probe (WMAP) and Planck studies of the Cosmic Microwave Background (CMB) have established beyond all doubt that our universe is spatially flat [1] [2] [3] . All non-flat cosmologies have thus been consigned to the waste basket of history. Andrew Lange, principle investigator for Boomerang, the first study to confirm universal flatness, was decidedly circumspect in his answer to the question on everyone’s mind: “Is this final confirmation that cosmic inflation theory is correct?”
One would do well to remember Lange’s admonition that one can never prove the correctness of cosmic inflation by confirming spatial flatness in the CMB. He emphasized that there might ultimately be other cosmology theories with a non-inflationary mechanism for achieving CMB flatness. While many scientists at the time considered Lange to be unnecessarily conservative with his answer, others have since reiterated this point of view. Physicist Philip Gibbs, for instance, put it this way: “The problem is that no particular model of inflation has been shown to work yet. It is possible that the work has not yet been completed or that a more recent specific model will be shown to be right” (emphasis mine) [4] .
Given Lange’s concerns, physicist Brian Keating and others have set out on a different tack by looking for inflationary B-mode polarization in the CMB. His new book [Keating (2018)] is an excellent glimpse into this new and exciting phase of experimental cosmology. Unfortunately, no primordial gravity waves of inflation have yet been discovered. In 2014, the BICEP2 team jumped the gun and prematurely announced a confirmatory result, only to be proven wrong by a Planck study overlay of B-mode polarizing interstellar dust.
While more sensitive searches for primordial gravity waves of cosmic inflation are being conducted, other cosmologists have taken up the cause of searching for non-inflationary mechanisms to explain cosmic spatial flatness. Some, like myself, have wondered if the universe has always been spatially flat since inception. Certainly, to this point, there is no observational proof otherwise. Even inflationary cosmologists agree that once the universe reaches critical density, it can remain spatially flat for the rest of time. We must remember that inflationary models must achieve spatial flatness to within one part in approximately 1060 before the first 10−32 second of cosmic time for inflation to achieve the degree of flatness now observed in the CMB [5] . This is a crucial realization. The only difference between an inflationary universe and a perpetually flat universe from inception is what happens within the first 10−32 second of cosmic time.
Flat Space Cosmology (FSC) is a remarkably accurate cosmological model which was initially developed as a heuristic mathematical model of the Hawking-Penrose conjecture [6] [7] that a universe smoothly expanding from a singularity can be theoretically treated within the rules of general relativity as a time-reversed black hole. Thus, it is perhaps not surprising that FSC makes predictions that closely fit with Planck survey observations. For instance, the Planck Collaboration reported an observed global Hubble parameter value of 67.8 +/− 0.9 km∙s−1∙Mpc−1 (68% confidence interval) and FSC predicts a current global Hubble parameter value of 66.89 km∙s−1∙Mpc−1, which fits the lower end of the Planck survey range. This FSC calculation is based only upon one free parameter, the Planck study fitting of the CMB temperature peak with a black body at 2.72548 K. This CMB temperature number, plugged into FSC equations first published in 2015 [8] [9] [10] [11] allows for a variety of cosmic parameter calculations fitting very tightly with observations [12] .
The five assumptions of FSC, closely adhering to the Hawking-Penrose conjecture, are as follows.
The Five Assumptions of Flat Space Cosmology
1) The cosmic model is an ever-expanding sphere such that the cosmic horizon always translates at speed of light
with respect to its geometric center at all times t. The observer is operationally-defined to be at this geometric center at all times
.
2) The cosmic radius
and total mass
follow the Schwarzschild formula
at all times
.
3) The cosmic Hubble parameter is defined by
at all times
.
4) Incorporating our cosmological scaling adaptation of Hawking’s black hole temperature formula, at any radius Rt, cosmic temperature
is inversely proportional to the geometric mean of cosmic total mass
and the Planck mass
.
is defined as twice the Planck length (i.e., as the Schwarzschild radius of the Planck mass black hole). With subscript
for any time stage of cosmic evolution and subscript
for the Planck scale epoch, and, incorporating the Schwarzschild relationship between
and
,
(1)
5) Total entropy of the cosmic model follows the Bekenstein-Hawking black hole formula [13] [14] .
(2)
The first two assumptions are based upon a literal interpretation of the Hawking-Penrose conjecture as it would pertain to a smoothly-expanding Schwarzschild black hole. The third assumption (Hubble parameter) treats maximally redshifted radial photons at the cosmic model horizon as moving with speed of light c relative to the geometric center at a distance of horizon radius Rt. This is a stipulation of relativity. The fourth assumption is a cosmic temperature scaling assumption. While it shows similarity to the static Hawking black hole temperature formula, the FSC cosmic model is treated as scaling in Planck mass increments. This allows for dynamic cosmic expansion modeling from the Planck scale epoch. Finally, the fifth assumption utilizes the Bekenstein-Hawking entropy definition, which seems appropriate for a model of the Hawking-Penrose conjecture.
As described in some detail in the seminal FSC papers [Tatum, et al. (2015)], the first three assumptions allow for perpetual Friedmann critical density (i.e., perpetual global spatial flatness) of the expanding FSC cosmological model from inception. By dividing the Schwarzschild mass (defined in terms of cosmic radius Ro) by the spherical volume, and substituting
with
,
Friedmann’s critical mass density
is achieved for any given moment
of observation (hence the subscript “o”) in cosmic time. So, perpetual Friedmann critical density from inception is a fundamental feature of the FSC model. Furthermore, because a Schwarzschild black hole is clearly allowed within the rules of general relativity, and because Hawking and Penrose have proven the validity of black hole time-reversal for modeling cosmological expansion, the FSC model, as defined by the rules of black holes, is clearly a general relativity model. A recent paper [15] has taken the FSC model further by integrating FSC into the Friedmann equations containing a Lambda
cosmological term. Thus, FSC has been shown to be a scalar dynamic
dark energy model of the wCDM type (wherein equation of state term w is always equal to −1.0). Furthermore, it is well-known that a sufficiently realistic Rh = ct linear model, such as FSC, can fit within the tightest constraints of the Supernova Cosmology Project (SCP) data. The following open source graph from the SCP (Figure 1) is offered as proof [16] .
One can readily see (by the “Flat” line intersection) that a realistic spatially flat universe model would be an excellent fit with all SCP observations to date.
Currently, there is no certainty about the percentage of the critical density which is attributable to dark matter. Those with knowledge of the observational studies of the ratio of dark matter to visible matter realize the difficulty of determining a precise co-moving value for this ratio at the present time. Galactic and perigalactic distributions of dark matter can be surprisingly variable, as evidenced by the 29 March 2018 report in Nature [17] of a galaxy apparently completely lacking in dark matter! Although the 2015 Planck Collaboration consensus is a large-scale approximate ratio of 5.3 parts dark matter to 1 part visible matter, this can only be considered as a rough estimate of the actual co-moving ratio, particularly if this ratio varies significantly over cosmic time. A 9.2-to-1 actual ratio in co-moving galaxies remains a possibility, and would change the ratio of total matter mass-energy to dark energy to essentially unity (i.e., 50% matter and 50% dark energy). Thus, the intersection zone of tightest constraints shown in Figure 1 would then correlate with 0.5 Omega_ matter and 0.5 Omega_Lambda. This is one of several important testable predictions discriminating
![]()
Figure 1. SCP supernovae, BAO and CMB data.
the FSC model from the standard cosmology model. Precise measurements of approximately co-moving galaxies are in order, for comparison with the Planck Collaboration result.
Furthermore, the question of dark energy dominance over total matter energy density remains in doubt. Several recent papers [18] [19] [20] [21] [22] have clearly shown that cosmic acceleration, however small, is not yet proven. These are not, of course, arguments against the existence of dark energy. They are only arguments placing some doubt on dark energy dominance, and thus cosmic acceleration, as opposed to cosmic coasting (as seen in all competitive Rh = ct models, such as FSC).
The above brief introduction to FSC is for the purpose of showing just one non-inflationary model which fits tightly with astronomical observations to date, including the flatness findings within the CMB. Thus, the words of Lange, Gibbs and Steinhardt [23] , who have had serious reservations about the certainty of cosmic inflation, are well worth remembering. Cosmic inflation is definitely not a certainty, particularly in light of the accumulating failures to confirm primordial inflationary gravity waves.
It is the purpose of this paper to present, in Section 2, the predictions and features of FSC which prove its superiority to standard inflationary cosmology. In fact, these predictions and features were embedded in FSC from its inception in 2015.
2. Predictions and Features of the FSC Model
2.1. Predictions Pertaining to Primordial Gravity Waves
FSC, by the arguments made above with respect to perpetual Friedmann critical density, can readily explain the flatness angular power spectrum of the CMB. Furthermore, this steadily expanding, finite but unbounded, model would not be expected to produce inflationary B-mode primordial gravity waves. Thus, FSC predicts that inflationary B-mode primordial gravity waves will never be confirmed. Such unequivocal confirmation of inflationary waves would falsify FSC. The continued failure to detect such waves (if the sensitivity of detection methods is sufficiently high) should be considered to strongly favor FSC over standard inflationary cosmology.
2.2. Cosmic Dawn Early Surprises
As noted in several recent papers [24] [25] [26] standard cosmology cannot easily explain surprisingly early star, galaxy and active galactic nuclei (i.e., quasars and blazars) formation. On the other hand, as detailed in the recent FSC paper entitled, “Temperature Scaling in Flat Space Cosmology in Comparison to Standard Cosmology” [12] , temperature differences between the two models are such that cosmic dawn in FSC may have developed as early as 20 million years after the Planck epoch versus approximately 110 million years in standard cosmology. The following graph (Figure 2) from the “Temperature Scaling” paper is presented for comparison, with features of the standard model as described in Bowman’s recent paper [24] .
Hashimoto’s paper [25] recently reported the difficulty of explaining their finding of an early galaxy at a redshift z value of 9.11 which suggested galaxy formation no later than about 250 million years after the Big Bang. And yet, a redshift z value of 9.11 is correlated with 174 million years in FSC versus 550 million years in standard cosmology (see how these cosmic times differ in Figure 2 above). Cosmic dawn in FSC would likely be at 20 - 50 million years after the Planck epoch (the so-called “Big Bang” in standard cosmology) as opposed to the standard cosmology cosmic dawn at 110 - 250 million years, as shown in Figure 2.
Thus, FSC is clearly superior to standard cosmology in terms of cosmic dawn early surprises.
2.3. Predicting the Magnitude of CMB Temperature Anisotropy
Standard cosmology has difficulty in providing a reasonable explanation for the magnitude of the observed CMB temperature anisotropy. Their current
![]()
Figure 2. Cosmic temperature vs time in standard cosmology (blue) and FSC (green).
explanation appears to be that the CMB pattern represents a magnified Big Bang “quantum fluctuation” event spayed out across the sky. Yet, modeling the physics of such a quantum fluctuation event, including predicting the actual magnitude of the CMB temperature anisotropy, eludes standard cosmology. This would require a deep understanding of quantum gravity, which is lacking at the present time, despite the admirable efforts of string theorists.
The angular power spectrum of the CMB clearly fits with a spatially flat universe. The Boomerang Collaboration reported CMB anisotropy observations closely fitting “the theoretical predictions for a spatially flat cosmological model with an exactly scale invariant primordial power spectrum for the adiabatic growing mode” [27] . Furthermore, the COBE DMR experiment [28] measured a CMB RMS temperature variation of 18 micro Kelvins. This translates to a dT/T anisotropy value of (0.000018)/2.725 equal to 0.66 × 10−5. This measurement fits within the range of FSC temperature anisotropy predictions for the beginning and ending of the recombination/decoupling epoch [29] . This result clearly favors FSC.
2.4. Predicting the Value of Equation of State Term w
For reasons to be described in “Flat Space Cosmology as a Model of Light Speed Expansion―Implications for the Vacuum Energy Density”, the FSC model requires that the equation of state w term have a value of exactly −1.0. This fits with the quantum field theory stipulation that the vacuum pressure
corresponding to the zero-state vacuum energy must always be equal in magnitude to the vacuum energy density
(i.e.,
). For reasons given in the FSC paper, a dark energy dominant universe (as currently believed in standard cosmology) would not meet this quantum field theory stipulation and would have a w value other than exactly −1.0. These are falsifiable predictions for both models. Standard model cosmologists believe our current universe to contain an extremely small net negative energy. In other words, they believe in slight cosmic acceleration (as opposed to constant velocity light speed expansion), despite current observations of global spatial flatness. However, if our universe began from a zero energy state, as is often assumed, and the universe now has a non-zero energy density, however small, this would appear to violate conservation of energy! Thus, there is tension in the standard cosmology model of dark energy dominance, because the Planck Collaboration has reported w = −1.006 +/− 0.045. A final consensus value of exactly −1.0, which seems highly likely at the present time, would be in support of FSC and falsify the current belief in dark energy dominance within standard cosmology.
2.5. Predicting the Hubble Parameter Value
In standard cosmology, the Hubble parameter value can only be determined by observation. That is to say that there is no theoretical ability within standard cosmology to derive a precise Hubble parameter value. The 2016 Planck Collaboration publication [30] reports the consensus global (i.e., CMB) Hubble parameter temperature and lensing value to be 67.8 +/− 0.9 km∙s−1∙Mpc−1 (at the 68% confidence interval). In FSC, the Hubble parameter is not a free parameter when a precise value of the CMB temperature is known. The c/Ro FSC value for the Hubble parameter can be determined by simply plugging the measured CMB temperature value To of 2.72548 K into relation 1B to get the current FSC radius Ro. Dividing speed of light c by Ro, according to FSC assumption #3, gives the metric value (s−1) of the Hubble parameter Ho, which converts to 66.89 km∙s−1∙Mpc−1. Thus, the observed CMB temperature and Hubble parameter values are tightly correlated by FSC theory alone!
Of note, another recently reported measurement of the Hubble parameter [31] is not truly global, but local in nature. Reiss, et al., by measurements based on Type Ia supernovae observations, did not observe the universe on its largest scale, as was the case for the Planck survey CMB observations. Furthermore, observational expectations and formulae for luminosity distance and angular diameter distance (with respect to redshift z) differ between the standard cosmology and Rh = ct linear models. This can result in the illusion of supernovae acceleration, if not correctly accounted for within the correct cosmological model (see Figure 3 and Figure 4 below and the discussion related to these figures). The obvious tension between the Planck CMB observations and Reiss’ supernovae observations, with respect to Hubble parameter measurements, may well be the result of such phenomena with respect to distant supernovae observations. In any event, Reiss’ outlier Hubble parameter value of approximately 73.24 km∙s−1∙Mpc−1 is not at all relevant to the global FSC model. The fact that FSC tightly correlates its theoretical Hubble parameter value (for a CMB temperature of 2.72548 K) with the observational Planck survey value is strongly in favor of FSC.
![]()
Figure 3. Relative luminosity distances vs. redshift z for standard (blue) and Milne (red) models.
![]()
Figure 4. Relative angular diameter distances vs. redshift z for standard (blue) and Milne (red) models.
2.6. Quantifiable Entropy and the Entropic Arrow of Time
One of the problems within the standard inflationary model is in quantifying cosmic entropy. Entropy is typically defined in terms of the total number of possible microstates and the probability of a given set of conditions with respect to that number of microstates. These values are impossible to quantify in an infinite-sized inflationary universe or multiverse. FSC, on the other hand, is a finite model with a spherical horizon surface area. Furthermore, since the Bekenstein-Hawking definition of black hole entropy would appear to apply to the FSC model, very precise values for cosmic entropy can be calculated for any time, temperature or radius of the FSC model. Thus, the “entropic arrow of time” is clearly defined and quantified in the FSC model [Tatum, et al. (2018)]. The quantifiable entropy of the FSC model allows for model correlations with cosmic entropy theories, such as those of Roger Penrose [32] and Erik Verlinde [33] . Thus, the entropy rules of FSC allow for falsifiability, whereas standard inflationary cosmology is not able to clearly define or quantify entropy or to establish falsifiability in terms of entropy. This feature favors the FSC model, particularly with respect to Verlinde’s “emergent gravity” theory described in the next section.
2.7. Clues to the Nature of Gravity, Dark Energy and Dark Matter
The reader is referred to the recent FSC paper [15] with this title for an in-depth discussion of how cosmic entropy in the FSC model provides for tantalizing clues with respect to the fundamental nature of gravity. In short, the FSC model is the cosmological model correlate to Verlinde’s “emergent gravity” theory [33] [34] . Verlinde’s landmark paper from 2011 provides strong theoretical support for gravity being an emergent property of cosmic entropy. The corresponding FSC paper makes a strong case for the correctness of Verlinde’s theory. The obvious implications for cosmology are huge. As discussed in the FSC paper, if gravity is an emergent property of cosmic entropy, then dark energy and dark matter are also likely to be emergent properties of cosmic entropy as well. The obvious implication is that galactic and perigalactic features attributed to dark matter (such as gravitational lensing and plate-like galactic rotation) could simply be a large-scale effect of the entropy of the visible galactic matter. Thus, the majority of what is currently being called dark matter may not actually be particulate in nature. If this turns out to be the correct interpretation, then the FSC model predicts that gravity, dark energy and dark matter may be no more definable at the quantum level than consciousness in two connecting neurons.
Following submission and acceptance of the “Clues to the Nature of Gravity, Dark Energy and Dark Matter” paper [15] , this author discovered the Brouwer, et al. observational reference [35] in support of Verlinde’s “emergent gravity” theory as it pertains to dark matter. The discovery of quantum gravity, other than quantum gravity somehow connected to entropy at the quantum level, would falsify Verlinde’s “emergent gravity” theory. At present, standard inflationary cosmology, by virtue of its inability to precisely define total cosmic entropy, has no capacity to incorporate Verlinde’s theory. This result clearly favors FSC, particularly in light of the above-mentioned observational findings typically ascribed to galactic and perigalactic dark matter.
2.8. The Cosmological Constant Problem
The “cosmological constant problem” is a longstanding problem in theoretical physics. It underscores standard cosmology’s longstanding problem with uniting general relativity with quantum field theory (QFT). Excellent expositions on this subject have been provided by Weinberg [36] and Carroll [37] . Suffice it to say, QFT predicts a cosmological constant value which differs from observational measurements of the vacuum energy density by a magnitude of approximately 10121! This discrepancy is so large that it is often referred to as the most embarrassing problem in all of theoretical physics.
In standard cosmology, it has been assumed that the energy density of the cosmic vacuum must be constant over the great span of cosmic time. However, general relativity does indeed allow for the vacuum energy density to be a dynamic scalar over time. Cosmological models incorporating scaling vacuum energy density are called “quintessence” models. FSC is one such model. In FSC, the vacuum energy density scales downward by 121.26 logs of 10 over the cosmic time interval since the Planck epoch. Perhaps of even greater interest is that the Bekenstein-Hawking cosmic entropy value scales upward in direct proportion to the expanding surface area of the cosmic horizon. If one were to count the current number of Planck radius microstates within the FSC horizon, the model indicates this entropy number to be 10121.26. Thus, once again, by virtue of the intimate relationship between vacuum energy (i.e., dark energy) and total cosmic entropy, FSC offers a clear-cut explanation for the magnitude difference between the Planck epoch vacuum energy density of the QFT theorists and today’s observed vacuum energy density of approximately 10−9 J∙m−3. Since the FSC model easily predicts these values, and standard inflationary cosmology has no basis for deriving them, the FSC model is clearly superior with respect to solving the cosmological constant problem.
2.9. Quantum Cosmology
The FSC model, by virtue of its appropriately scaling cosmic temperature equation (the first equation listed under FSC assumption #4), can be considered the first successful quantum cosmology model [Tatum, et al. (2015)]. By incorporating the values of T0,
, G, kB, Lp, and
to as many decimal places as known, the FSC parameters can be shown to closely match astronomical observations, as detailed in the FSC paper entitled, “Temperature Scaling in Flat Space Cosmology in Comparison to Standard Cosmology” [12] . For convenience, the most important FSC quantum cosmology equations are repeated below:
(3)
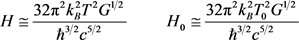 (4)
(4)
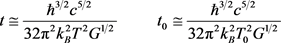 (5)
(5)
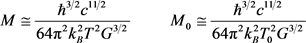 (6)
(6)
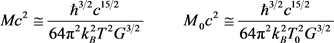 (7)
(7)
Current parameters are calculated in the right-hand column. As previously mentioned, the only free parameter in any of these equations is the cosmic temperature. The currently-observed cosmic temperature value: T0 = 2.72548 K. It is truly remarkable that, using only current best measurements of the CMB temperature, the Ho value in Equation (4) can be calculated and fitted to the lower end of the Planck Collaboration observational measurement!
No quantum model exists for standard inflationary cosmology. This obviously favors the FSC model.
2.10. Dark Matter and Dark Energy Quantitation
As detailed in the Planck Collaboration report, the ratio of dark matter to visible (baryonic) matter is observed to be approximately 5.3 parts dark matter to 1 part visible matter. However, so little is currently known about precisely detecting and quantifying dark matter that this ratio is subject to higher revision in the likely event that more dark matter is discovered in the future. For this reason, the Planck Collaboration ratio must be considered as a constraint only on the low end. Moreover, there are differences between dark matter-to-visible matter ratios observed within galaxies quite near to us (essentially co-movers) and the aforementioned dark matter-to-visible matter ratio determined from Planck survey CMB observations. If the co-moving ratio is ultimately found to be slightly higher by less than a factor of two, to 9.2 parts dark matter to 1 part visible matter (for co-moving galaxies), one can then conclude that total matter energy density at present is equal in absolute magnitude to dark energy density. This equality of opposite sign energy densities is what one would expect for a flat universe. Otherwise, if one energy density dominated the other, there should be detectable global spatial curvature corresponding to the dominating energy density. One could, in fact, make a very strong case that the unequivocal spatial flatness of the CMB proves the equality of total matter and dark energy densities at the time of the recombination/decoupling epoch. This should nullify any Planck Collaboration conclusions (such as dark energy dominance) which are obviously contrary to their own observations of flatness.
Despite the fact that FSC and standard cosmology differ slightly with respect to the exact percentages of total matter vs. dark energy, there is one thing about this energy density partition on which everyone agrees: it is truly remarkable that total matter energy density and dark energy density are of the same order of magnitude at the present time. As physicist I. I. Rabi once famously remarked, “Who ordered that?!” Standard cosmology simply accepts this “coincidence problem” with no further explanation or rationale. However, FSC stipulates perpetual equality of absolute magnitude of these two energy densities as a requirement for a spatially flat universe. More importantly, this is a stipulation of the global spatial curvature rules of general relativity, as discussed in some detail in recent FSC papers [Tatum, et al. (2018)]. One can consider this expectation of energy density equality to be a falsifiable FSC prediction with respect to future measurements of total matter energy density vs dark energy density.
With respect to standard cosmology’s current belief in cosmic acceleration due to dark energy, the reader is referred to references [18] thru [22] mentioned earlier in this paper. Cosmic acceleration is clearly not proven at the present time, despite the indisputable presence of dark energy. The reader is also referred to this author’s recent publication in Journal of Modern Physics entitled, “How a Realistic Linear Rh = ct Model of Cosmology Could Present the Illusion of Late Cosmic Acceleration” [38] . There are relative differences in luminosity distance and angular diameter distance formulae in standard cosmology and Rh = ct modified Milne-type models (like FSC). Two comparative graphs from this paper are repeated in Figure 3 and Figure 4.
The significance of the relative luminosity distance and relative angular diameter distance comparisons between these two competing models is paramount. An observer of distant Type Ia supernovae expects particular luminosity distances and angular diameter distances to correspond with particular redshifts. If instead he or she observes greater-than-expected luminosity distances (i.e., unexpected “dimming” of the supernovae) or greater-than-expected angular diameter distances, this can easily be misinterpreted by a standard model proponent as indicative of cosmic acceleration. However, entirely predictable supernova luminosity distances within a realistic Milne-type universe containing matter, as opposed to a standard model universe, could be one possible explanation for the Type Ia supernovae observations since 1998. Obviously, cosmic acceleration would not then be required to explain these observations. This possibility, combined with the standard model tension problem presented above (i.e., spatial flatness and dark energy dominance cannot both be true at the same time), and the FSC stipulation for what the standard model calls the “coincidence problem,” strongly favors FSC with respect to its predictions concerning dark matter and dark energy quantitation.
2.11. Requirements for New Physics
Inflationary theories require that there be a mysterious pre-gravity energy field (called the “inflaton”), which rolls downhill after the moment of the Big Bang and nearly instantaneously inflates the nascent universe to such a size that deviations from global spatial flatness cannot be observed even 14 billion years after the Planck epoch. Standard cosmology maintains that a quantum fluctuation event within a zero energy pre-Big Bang state kicked off the universal expansion. It also maintains that gravity was the first of four fundamental forces to “freeze out” following an exceedingly brief exponential inflationary phase. Standard model cosmologists believe our current universe to contain an extremely small net negative energy. In other words, they believe in cosmic acceleration (as opposed to constant velocity light speed expansion), despite observations of extreme flatness. However, if our universe began from a zero energy state, and now has a net negative energy density, however small, this would appear to violate conservation of energy! Furthermore, one must ask what exactly is the nature of the force represented by the inflaton field, specifically if gravity did not already exist at the inception of the universe. Cosmic inflation energy appears to be suspiciously like early cosmic dark energy, which we know to be negative gravitational energy in nature. The Big Bang theory is derived from general relativity, which is entirely a gravity theory. To require that a gravity theory incorporates a pre-gravity phase within its cosmology, however brief in duration, sounds very much like nonsense. Moreover, cosmic inflation is an ad hoc theory “… contrived with the goal of arranging for the density perturbations to come out right” [Guth (1997), page 238]. Cosmic inflation, in its many different ad hoc forms, appears to be a deeply flawed theory, as nicely elaborated by one of its founders [Steinhardt (2011)].
Needless to say, a great deal of new physics appears to be required by inflationary cosmology. Not only would a new energy field with ad hoc features be required before gravity “freezes out,” but, somewhere along the way, conservation of energy would need to be violated. This must be true if the universe started from zero energy (Guth’s “free lunch” idea) and ended with endlessly increasing dark energy dominance. It must be remembered that inflationary theories preceded the discovery of dark energy.
According to the FSC model, dark energy density of the early universe was at a remarkably high negative value in balance with the remarkably high positive energy density of matter. Thus, the “repulsive gravity of the inflaton” idea can be seamlessly replaced by FSC’s incredibly high dark energy density in the early universe. The reader is reminded that, even in the seminal FSC paper from 2015, the model expands 25 logs of 10 within 10−17 second. FSC’s smoothly progressing light speed expansion does not have the nearly-instantaneous, transient and explosive nature of cosmic inflation. Thus, a future unequivocal discovery of explosive primordial gravity waves is not predicted by the FSC model. Along the lines previously mentioned by Stephen Hawking, cosmic expansion may, in fact, be unbounded in time, with no Big Bang beginning event whatsoever. Whatever may be the case, FSC maintains perpetual spatial flatness, as defined by Friedmann’s critical density, and does not require a poorly-understood explosive mechanism to achieve critical density.
Accordingly, FSC does not appear to require any new physics and does not appear to violate conservation of energy. The global energy-density tally is perpetually maintained at a net value of zero, as required for a spatially flat expanding universe acting as an isolated system not influenced by external forces. For these reasons, FSC appears to be superior to standard cosmology with respect to requirements for new physics.
3. Summary and Conclusions
Following recent precise CMB observations of global spatial flatness, only two types of viable cosmological models remain: inflationary models which almost instantaneously attain cosmic flatness following the Big Bang; and non-inflationary models which are spatially flat from inception. FSC is the latter type of cosmological model by virtue of assumptions corresponding to the Hawking-Penrose conjecture that a universe expanding from a singularity could be modeled like a time-reversed black hole. Since current inflationary models have been criticized for their lack of falsifiability, the numerous falsifiable predictions and key features of the FSC model are herein contrasted with standard inflationary cosmology. For the reasons given, the FSC model is shown to be superior to standard cosmology in the following eleven categories: Predictions Pertaining to Primordial Gravity Waves; Cosmic Dawn Early Surprises; Predicting the Magnitude of CMB Temperature Anisotropy; Predicting the Value of Equation of State Term w; Predicting the Hubble Parameter Value; Quantifiable Entropy and the Entropic Arrow of Time; Clues to the Nature of Gravity, Dark Energy and Dark Matter; The Cosmological Constant Problem; Quantum Cosmology; Dark Matter and Dark Energy Quantitation; Requirements for New Physics.
Dedications and Acknowledgements
This paper is dedicated to Stephen Hawking and Roger Penrose for their groundbreaking work on black holes and their possible application to cosmology. Dr. Tatum also thanks Rudolph Schild of the Harvard Center for Astrophysics for his support and encouragement.