1. Introduction
In this note we give a complete proof of the following theorem of Dedekind. Our proof is a somewhat detailed version of the one given in Basic Algebra by Jacobson, Volume I, [1] and we shall keep the notations used in that proof.
Theorem 1 Let
be square-free monic polynomial of degree n and p be a prime such that p does not divide the discriminant of
. Let
be the Galois group of
over the field
of rational numbers. Suppose that
factors as:
where
are distinct monic irreducible polynomials in
, degree
,
, and
.
Then there exists an automorphism
which when considered as a permutation on the zeros of
is a product of disjoint cycles of lengths
.
2. Preliminary Results
We shall assume that the reader is familiar with the following well-known results.
1) Let
be a field and
be a polynomial of degree
. Then any two splitting fields of
are isomorphic.
2) A finitely generated Abelian group is direct sum of (finitely many) cyclic groups. (This is the fundamental theorem of finitely generated Abelian groups).
3) A system of n homogeneous equation in
variables has a non-trivial solutions.
4) Let
be an algebraic extension. Then any subring of
containing
is a subfield of
. Proof: Let K be a ring such that
. Let
. As
is algebraic over
,
. So
.
5) (Dedekind’s Independence Theorem). Distinct characters of a monoid (a set with associative binary operation with an identity element) into a field are linearly independent. That is if
are distinct characters of a monoid into a field
, then the only elements
,
, such that
for all
are
,
.
6) Let p be a prime and
be a finite field with
elements. Then the group
is cyclic of order m and the generating automorphism
maps
to
.
7) If R is a commutative ring with identity and M is a maximal ideal of R then R/M is a field.
8) Let
. Then
and
have same cyclic structure.
Let
be a polynomial of degree
, and p a prime number. Then
will denote the polynomial obtained by reducing the coefficients of
modulo p.
Theorem 2 Let
be a monic polynomial of degree
and p be a prime number which does not divide the discriminant of
. Let
be a splitting field of
over
. Let
be a splitting field of
over
. Let
where
,
are the roots of
and
Let
be the subring generated by the roots of
of
in
. Then
• 1) There exists a homomorphism
of D onto
.
• 2) Any such homomorphism
gives a bijection of the set R of the roots of
in
onto the set
of the roots of the
in
.
• 3) If
and
are two such homomorphisms then there exist
, such that
. (Note that the restriction of
to D is an automorphism of D).
Proof 1) One has that:
We claim that
is a finitely generated (additive) Abelian group. Since each
is a root of the monic polynomial
of degree n any positive power of
can be expressed as an integral linear combination of
. It follows that
Therefore D is a finitely generated (additive) Abelian group generated by at most nn elements. By the Fundamental Theorem for Finitely Generated Abelian Groups D is a direct sum of finitely many cyclic groups. Since
, none of these cyclic groups is finite. So D is a direct sum of finitely many infinite cyclic groups. Let
be a set consisting of an independent generating system of D. We have
We claim that
is a basis of
. Obviously
is linearly independent over
. Let
. Then
is a ring and
therefore
is a field. Since
for
, by (4)
and
is a basis of
. As
,
is an ideal of D and
Therefore the
is finite of order
. Let M be a maximal ideal of D containing pD. That is
and
is a finite field of characteristic p and so it has a subfield isomorphic to
which we will identify as
in what follows. As
the order of
is
,
. Consider the canonical epimorphism
whose kernel is M and
. Therefore
. We note that as
we have for
As
is an epimorphism we have
is a splitting field of
over
. As both
and
are splitting fields of
over
they are isomorphic. Let
be such an isomorphism. Then
is a homomorphism of D onto
.
2) Let
be a homomorphism. So
. As
, and
has characteristic p,
, so
.
can be extended to a homomorphism of the polynomial rings
. Under this mapping
. As
are the roots of the
in
and therefore the restriction of
to R
is a bijection of the set R of roots of
in
to the set
of the roots of
in
.
3) We have seen that given a homomorphism
, and
,
is also a homomorphism from D to
. We note that the restriction of
to
is also an automorphism of the ring D. Since
, the group
has order N. Let
So given a non-trivial homomorphism
, we get N distinct homomorphisms
,
, from D to
. We claim that these are all the homomorphisms from D to
. Suppose that there is a homomorphism from D to
which is different from
,
. Let us denote it by
. By Dedekind Independence Theorem the set
of
homomorphisms from D to
is linearly independent over the field
.
Consider the following system of N homogeneous equations in
variables
,
Since there are more variables than the equations this system of equations has a non-trivial solution. Let this non-trivial solution be
,
. So we have
Let
. So
,
,
. Then for
we have
where
. We shall show that
which will contradict the linear independence of
over
.
3. Proof of the Main Theorem
Since the field
has order
, the group
has order m and
where
for all
, is the generating automorphism of
. So if
is any homomorphism then so is
. Since
and
are two homomorphisms from D to
there exist
such that
or
. This proves that the action on
on
is similar to the action of
on
. Note: In the following diagram the mapping
is the restriction of
to D and we are only concerned with the effect of the mappings
,
and
on
and
. Clearly
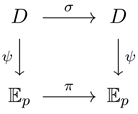
As
and
the effect of
on
is similar to the effect of
on
. This is further illustrated by the following: