Impact of Channel Dynamics, Combined Nonlinearities and ASE Noise on Transmission Performance of all Optical Star WDM Networks ()
For all optical Wavelength Division Multiplexing (WDM) network based on G.653 fibers, we investigate the quality factor deterioration due to combined nonlinear effects and Amplified spontaneous emission (ASE) noise for system parameters based on ITU-T Recommendation G.692. The investigation: 1) emphasizes on stimulated Raman scattering (SRS) and four wave mixing (FWM) effects which are the dominant nonlinearities known to limit WDM system performance and 2) accounts for beating between nonlinearities and beating between ASE noise and nonlinearities. Using the proposed model, performance of the worst affected channels due to SRS and FWM is compared and the results indicate that the worst affected channel due to SRS performs better and hence must be preferred for reliable and efficient transmission over the worst affected channel due to FWM. Further, the results suggest that to achieve a desired error rate (quality factor); there exists an optimal value of channel spacing for a given number of channels. The proposed theoretical model is also validated through extensive simulations over Rsoft OptSimTM simulator and the two sets of results are found to match, indicating that the proposed model accurately calculates the quality factor of the all optical WDM network.
1. Introduction
Optical communication based on Wavelength-Division multiplexing (WDM) is progressing at an astonishing rate due to the possibility of high transmission capacity. In WDM systems, the entire optical bandwidth is divided into a number of channels centered at different wavelengths that allows many light beams of distinct wavelengths to be simultaneously sent into the core of the fiber [1]. Thus, WDM systems dominate long-haul and ultra-long-haul networks due to both performance and cost advantages. Erbium-Doped Fiber Amplifiers (EDFAs) are used to compensate signal attenuation in longdistance transmission, thus allowing high-data rate transmission over a long distance. The high optical power level available from EDFAs leaves the system performance more vulnerable to various nonlinear effects [2]. Attempts made to utilize the large bandwidth provided by the optical fiber along the WDM links are hindered by the accumulation of fiber nonlinearities and amplified spontaneous emission (ASE) noise due to EDFAs [3], thus making the performance limitations imposed by these effects an important area of study. Among the fiber nonlinearities known to limit the throughput of the WDM transmission system, stimulated Raman scattering (SRS) and four-wave mixing (FWM) are the dominant effects [4]. Figure 1 shows the power representation due to FWM and SRS effects as it appears at the output when 3 channels with equal powers at wavelengths λ1, λ2 and λ3 respectively are the input to an optical fiber WDM system.
The two conventional limiting factors in the design of WDM systems, namely, fiber loss and dispersion, are relatively well understood, and can be easily overcome by optical amplifiers and dispersion compensation. The influence of fiber nonlinearities on the other hand, have not been fully analyzed and understood despite a rich collection of literature involving extensive studies deal-

Figure 1. SRS and FWM impairments in an optical WDM network as a limiting power degradation factor.
ing with the nonlinear effects on system performance [5-12]. Also, most investigations of nonlinear effects on WDM systems have primarily been done independently of each other i.e. most works focus on the individual effects of nonlinearities and ASE noise on various system parameters.
The transmission engineering of high speed and wavelength-rich WDM networks though, requires an in-depth understanding of the collective nonlinear effects and their interplay with the accumulated ASE noise in order to identify their impact on Q-factor and to reliably conclude on the system penalty. Few works consider the combined effects of nonlinearities in the presence of ASE noise on WDM system performance. Djordjevic [13] derived simple expressions to study the transmission limitations imposed by SRS, FWM and ASE noise in a WDM system with dispersion compensated links using inline optical amplifiers. The results are presented for data rates of 2.5 Gbps and 10 Gbps with different dispersion compensation maps and the maximum possible transmission distance in terms of various system parameters is discussed. The study, however, ignores the beat terms that arise due to optical nonlinearities themselves, as well as the beating between nonlinearities and the ASE noise and assumes that no channel suffers more than 1 dB signal power depletion due to SRS.
Yu and Mahony [14] have studied the transmission limitations imposed by the combined effect of SRS, FWM, ASE noise and fiber dispersion. The optimum values of amplifier spacing, number of wavelength channels and channel spacing are calculated at the data rate of 2.5 Gbps. The analysis considers FWM and SRS effect with emphasis on the former and concludes that a compromise is needed between conflicting requirements imposed by FWM and SRS effects in terms of channel spacing for a given number of channels to maximize the transmission distance. The authors have performed the analysis to evaluate the transmission distance limitation as a function of various system parameters ignoring the beating between ASE noise and the nonlinearities.
Tariq and Dhodhi [15] evaluated the limitations on long-haul WDM network due to SRS and ASE noise and have drawn the conclusion that the total link length is determined by the signal-to-noise ratio of the worst affected channel due to SRS while the total link length can be increased by reducing the optical amplifier gain, thus increasing the number of amplifiers. The study reports the results for BER of the channel worst affected by SRS but ignores the effect of FWM.
Singh, Kar and Jain [16] made a comparative study of various amplifier configurations considering FWM and concluded that the placement of optical amplifier as an inline amplifier is the optimal position as it requires minimum power for a given probability of error. An extension to the study in [16] is presented by the same authors in [17] where the effect of FWM, ASE noise and wavelength converter noise on the performance of WDM all-optical networks is investigated. The results indicate that in presence of FWM, after a certain power level, the performance of the all-optical network starts degrading. The analysis for the evaluation of probability of error has been carried out in the absence of SRS effect.
Singh and Iyer [18] have analyzed the performance of an optical star network considering the combined effect of FWM and SRS noise. It was observed that the network performance depends on FWM noise and power received at the receiver due to SRS. An intensity-modulated/direct-detection (IM/DD) system with N equally spaced channels is considered for the analysis that takes into account the beating between SRS and FWM but does not account for their interplay with ASE noise.
In this paper, we present an extension of the work in [18] and develop a mathematical model to evaluate the performance of an optical star network considering the combined effect of FWM, SRS and ASE noise. We consider an intensity-modulated/direct-detection (IM/DD) system with N channels which are equally spaced and have equal power. Since the number of channels is large, the effect of SRS is assumed to be deterministic and the Raman gain profile is assumed to be triangular [4]. The novelty of the work is that our model accounts for beating between nonlinearities and beating between ASE noise and nonlinearities. Further, the developed model is used to compare the performance of the worst affected channels due to SRS and FWM based on ITU-T G.692 Recommended parameters.
We performed extensive simulations over Rsoft OptSimTM simulator in order to to validate the theoretical results which were obtained using the proposed model. It has to be mentioned that these simulations were very time consuming, more than 1 week on a dual core 2.20 GHz computer with 1 GB of RAM just to measure the Q-factor at different transmitted power values for a specific channel separation. With increase in system length, the simulation time increased considerably. Keeping in view the long simulation time, we set the value of length of the fiber between star coupler to 120 km as mentioned in Table 1. It has to be pointed out that even if the length is altered, the conclusions derived from the obtained results will remain the same. The reason for this can attributed to the fact that when length of the fiber is increased, FWM generated components will also increase and will interact considerably leading to FWM becoming the more dominant effect compared to SRS, as a result of which the worst affected channel due to FWM will give degraded performance compared to the worst affected channel due to SRS. Also, it has been shown experimentally in [4] that when three equally spaced channels with modest power level of 3 mW respectively are launched at the input of a short 25-km dispersion-shifted fiber (DSF), substantial impairment due to FWM occurs. Therefore, when the length is decreased, FWM will still be the dominant effect. Hence, the conclusions derived in this paper will apply to all optical WDM systems with any arbitrary chosen value of system length.
The paper is organized as follows. Section 2 describes the system model. In Section 3, we present the mathematical model to evaluate the performance of the alloptical star network in terms of Q-factor when FWM, SRS and ASE noise are present and the worst affected channel is due to SRS. Section 4 presents the performance evaluation of the network when FWM, SRS and ASE noise are present and the worst affected channel is due to FWM. The simulation model setup to validate the results from the theoretical approach is described in Section 5. Finally, Section 6 discusses the numerical results and the conclusion.
2. System Model
The network shown in Figure 2 consists of two passive star couplers, one at the transmitter and the other at the receiver.
The star couplers distribute the input power equally among all the N output ports. The optical fiber considered is a single mode non-zero dispersion shifted fiber with dispersion and attenuation values of 17 ps/nm·km and 0.2 db/km respectively. The amplifier is used as an inline amplifier and is considered to have a uniform gain G over the optical bandwidth B0. Apart from amplifying the signal, the amplifier will also generate ASE noise. When the ASE noise and signal are incident on a photo detector at the receiver, the noise beats with itself and also with the signal. As a result ASE-ASE, ASE-signal and ASE-shot beat noise components are generated. Since our analysis also accounts for FWM, ASE-FWM beat noise component will also be generated. Each receiver receives the signal on all the wavelengths and the optical filter is used to filter out the required wavelength. The received signal is then detected with the help of a photo detector. Let 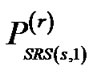 represent the signal power at the 1st receiver at frequency f1 and
represent the signal power at the 1st receiver at frequency f1 and  represent the signal power at the jth (center) receiver at frequency fj. Let Pt denote the transmitted power. Data bits “1” and “0” are transmitted as a “mark” and “space” respectively and the signal power for bit “0” has been assumed to be zero.
represent the signal power at the jth (center) receiver at frequency fj. Let Pt denote the transmitted power. Data bits “1” and “0” are transmitted as a “mark” and “space” respectively and the signal power for bit “0” has been assumed to be zero.

Figure 2. Optical star network with amplifier.
3. Performance Evaluation of the Worst Affected Channel Due to SRS Considering the Combined Effect of FWM, SRS and ASE Noise
The effect of SRS will cause the power of the 1st channel to be transferred between channels 2 to N. Thus, maximum power will be depleted from the 1st channel due to SRS. The combined effect of FWM and ASE noise on this channel will further degrade the signal quality. Hence, the 1st channel is considered for performance evaluation in this section. The signal power  at the 1st receiver in terms of transmitted power Pt is given by
at the 1st receiver in terms of transmitted power Pt is given by
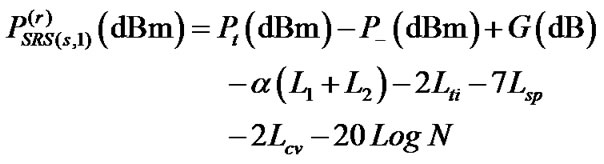 (1)
(1)
where represents the depleted power, α the fiber loss coefficient in dB/km, Lsp the splicing loss (at splices marked as “/” in Figure 2), Lcv the loss due to non-uniformity in power splitting by the star coupler and Lti the total insertion loss of the star coupler. In (1),
represents the depleted power, α the fiber loss coefficient in dB/km, Lsp the splicing loss (at splices marked as “/” in Figure 2), Lcv the loss due to non-uniformity in power splitting by the star coupler and Lti the total insertion loss of the star coupler. In (1),  is given as
is given as
 (2)
(2)
The total electric field at the receiver will be given by
 (3)
(3)
where is a random phase for each component of spontaneous emission. In (3), the first term is the electric field due to signal component while the second and third terms represent electrical field due to FWM and ASE noise respectively. In the above expression,
is a random phase for each component of spontaneous emission. In (3), the first term is the electric field due to signal component while the second and third terms represent electrical field due to FWM and ASE noise respectively. In the above expression, 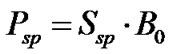
and . The receiver current for bit “1” i1(t) (i.e. Bs = 1) is given by
. The receiver current for bit “1” i1(t) (i.e. Bs = 1) is given by
 (4)
(4)
where Equation (5).
In the above equation, Ssp represents the power spectral density of ASE noise and is given by
 (6)
(6)
where is the spontaneous emission factor and ranges from 1.4 to 4 for EDFA. The parameter
is the spontaneous emission factor and ranges from 1.4 to 4 for EDFA. The parameter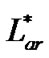 represents the loss for the ASE noise between amplifier and the receiver and is given as
represents the loss for the ASE noise between amplifier and the receiver and is given as
 (7)
(7)
or
 (8)
(8)
In (5), first term represents the signal. The second term gives rise to ASE-shot beat noise and ASE-ASE beat noise, third term ASE-signal beat noise, fourth term FWM-ASE beat noise and fifth term FWM-signal beat noise respectively. The third, fourth and fifth terms have zero mean. The receiver current for bit “1” will be the sum of currents due to individual components and thermal noise. Hence, the mean value of current i1(t) represented as  is given by
is given by
 (9)
(9)
The noise variance for bit “1” is
 (10)
(10)
where Be is the ideal electrical filter bandwidth in the receiver and Equation (11).
 (5)
(5)

(11)
The expression for R0 E2(t) when bit “0” (i.e., Bs = 0 and  = 0) is transmitted is given as
= 0) is transmitted is given as
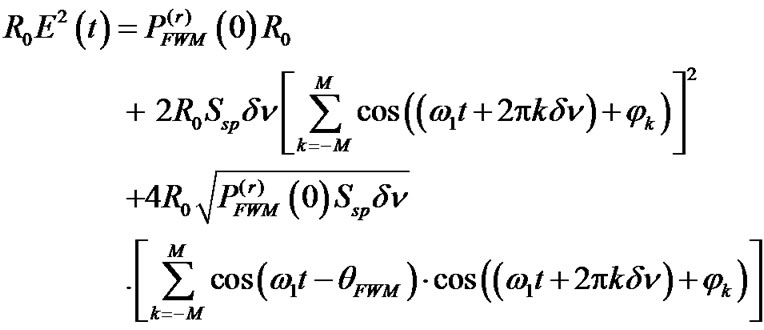
(12)
Hence, the mean value of current i0(t) represented as  is given by
is given by
 (13)
(13)
where [16]
 (14)
(14)
The noise variance for bit “0” is
 (15)
(15)
In (15),  has the terms in order of
has the terms in order of  which is very small and can be neglected. Thus
which is very small and can be neglected. Thus
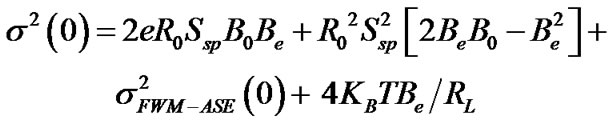 (16)
(16)
where
 (17)
(17)
The probability of bit error, which specifies the average probability of incorrect bit identification, is given as [3]
 (18)
(18)
The Q-factor specifies the performance in an optical communication system as it is related to signal to noise ratio to achieve a specific probability of bit error. The Q-factor is given as
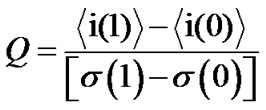 (19)
(19)
For probability of error of 10–9, value of Q is 6. Substituting ,
,  from (9) and (13) into (19), we obtain Equation (20).
from (9) and (13) into (19), we obtain Equation (20).
Once σ(1) and σ(0) are known,  can be determined for a given Q (or Pe) from (20). With this value of
can be determined for a given Q (or Pe) from (20). With this value of , corresponding Pt can be determined from (1).
, corresponding Pt can be determined from (1).
4. Performance Evaluation of the Worst Affected Channel Due to FWM Considering the Combined Effect of FWM, SRS and ASE Noise
Since maximum number of FWM components are generated at the central channel [11], the worst affected channel due to FWM will be the central channel. Let the jth channel represent the central channel. Hence, the central (jth) channel is considered for performance evaluation in this section. The effect of SRS at the jth channel leads to power reception from channels 1 to j – 1 and power transfer to channels j + 1 to N. The depleted and the gained powers represented as and
and are given as
are given as
 (21)
(21)
and
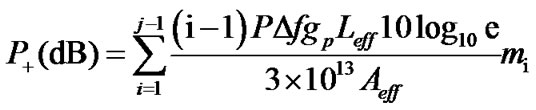 (22)
(22)
respectively. The signal power 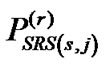 at the
at the receiver will be
receiver will be
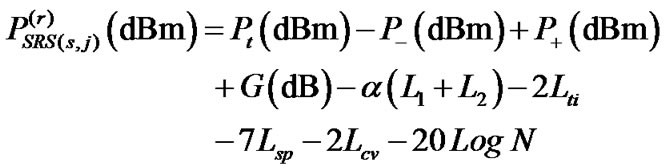 (23)
(23)
The total electric field at the receiver in this case is given by
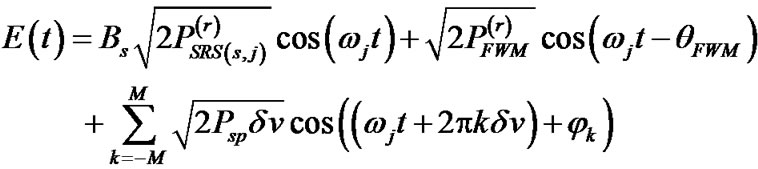
(24)
 (20)
(20)
where the first term is the electric field due to signal component while the second and third terms represent the electrical field due to FWM and ASE noise respectively.
The mean value of current for bit “1” is given by
 (25)
(25)
The noise variances for bit “1” is
 (26)
(26)
or
 (27)
(27)
The expression for R0 E2(t) when bit “0” (i.e., Bs = 0 and = 0) is transmitted is
= 0) is transmitted is
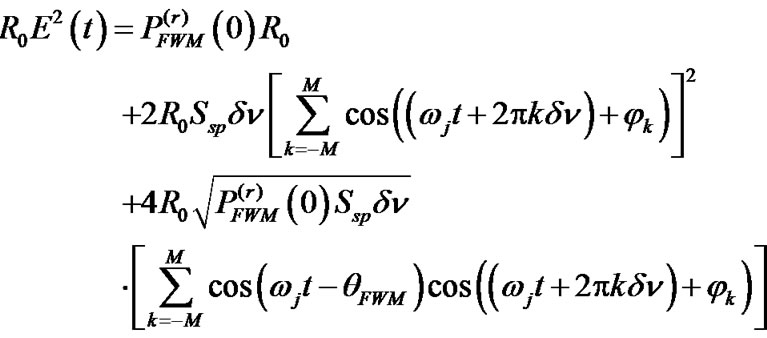
(28)
Hence, the mean value of current i0(t) represented as  is given by
is given by
 (29)
(29)
where is as given in Equation (14). The noise variance for bit “0” is
is as given in Equation (14). The noise variance for bit “0” is
 (30)
(30)
where  is as given in (17). Substituting
is as given in (17). Substituting ,
,  from (25) and (29) into (19), we obtain Equation (31).
from (25) and (29) into (19), we obtain Equation (31).
Once σ(1) and σ(0) are known,  can be determined for a given Q (or Pe) from (31). With this value of
can be determined for a given Q (or Pe) from (31). With this value of , corresponding Pt can be determined from (23).
, corresponding Pt can be determined from (23).
5. Simulation Setup and Description
In order to evaluate the exactness of the theoretical results, we conducted extensive computer simulations of 8 and 16 channel WDM transmission systems based on ITU-T G.692 recommendation [19] for applications on G.653 fibers [20]. We used the commercial package Rsoft OptSimTM simulation software (Version 4.0) that gave us the environment almost like the exact physical realization of a WDM system. OptSim provided us with laser diodes, filters, modulators, fiber and photo detectors which are the essential components to build an optical network. The simulated system for an 8 channel WDM system is shown in Figure 3 and the same system was extended by adding 8 more channels in order to simulate a 16 channel WDM system. The channels are modulated at 10 Gbps data rate using NRZ format and the optical frequency distribution is based on the 100 GHz and 50 GHz ITU-T G.692 Recommendation frequency grid. The analysis concerns the ‘worst case’, i.e. the case of the 1st and jth (center) channel with the simultaneous presence of “1” bits in all the other channels. The simulation system shown in Figure 3 consists of three major sections, i.e., transmitter section, fiber section and receiver section which are described next.
5.1. Transmitter Section
The transmitter consists of a pseudo random bit sequences (PRBS) generator, which generates PRBS at the rate of 10 Gbps with 16 samples per bit using polynomial of degree 7. The bit sequence is fed to the NRZ coder that produces an electrical NRZ coded signal. The NRZ driver converts the input to electrical outputs “0” for low level and to “1” for high level. The source used is a CW Lorentzian laser source and the system has been designed around central wavelength of 1550 nm. The Modulator used is a single arm Mach-Zehnder amplitude modulator with sin2 electrical shaped input-output (P-V) characteristics to convert the electrical signal into optical signal. It has two inputs, one for the laser diode and the other for the data from the channels.
 (31)
(31)
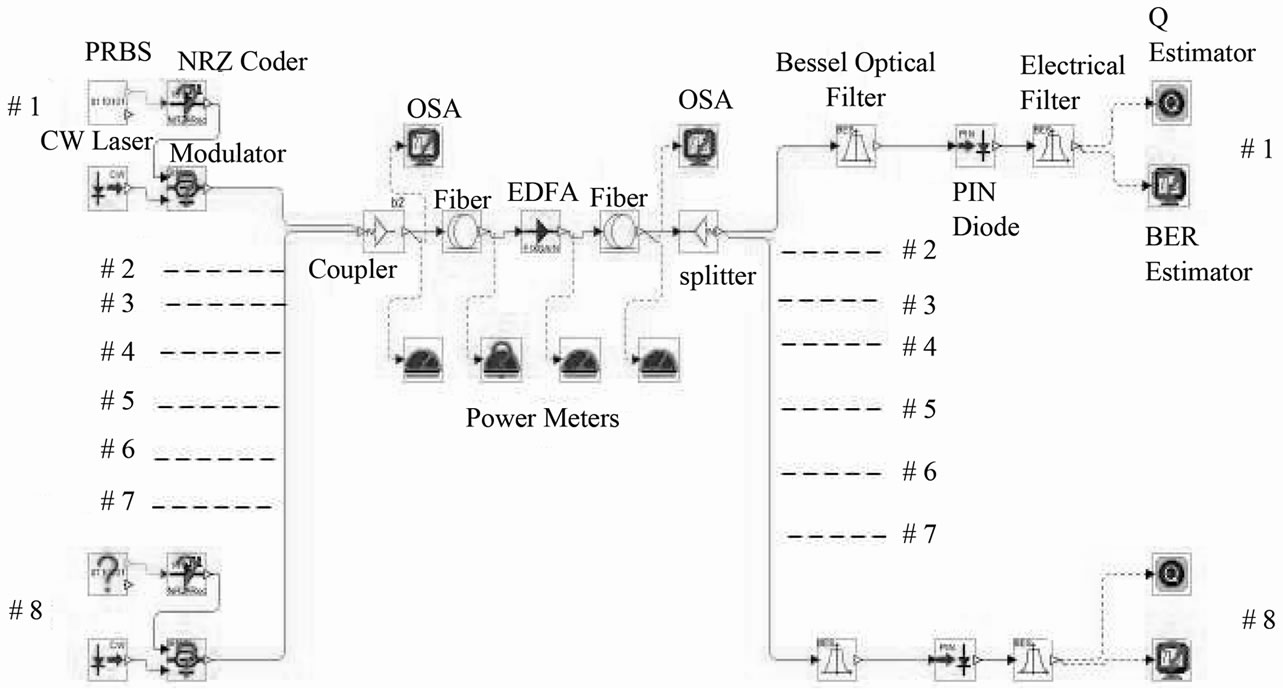
Figure 3. Architecture of the analyzed 8-channel WDM system.
5.2. Fiber Section
Signals from transmitters are combined using an optical coupler. This combined optical signal is fed into a single mode non-zero dispersion shifted fiber with dispersion and attenuation values of 17 ps/nm·km and 0.2 db/km respectively at the reference frequency. The length, nonlinear index and core area of the fiber are as per the values given in Table 1. The fiber model in OptSim takes into account the unidirectional signal flow, SRS, FWM and dispersion. The FWM effect is considered by defining the nonlinear coefficient  for the fiber as [21]
for the fiber as [21]
 (32)
(32)
where n2 is the Kerr nonlinear index coefficient, ω the angular optical frequency, Aeff the effective core area, and c the light velocity in vacuum. A Fixed gain optical amplifier is used which sets the amplifier gain to 20 dB with flat gain shape and noise figure value of 4.5 dB. The distance between the first fiber and the EDFA is 80 km and that between the EDFA and the second fiber is 40 km which makes the total fiber length equal to 120 km. The optical spectrum analyzer (OSA) and the power meter are used to view the optical spectrum and the power of the signal at various points as shown in Figure 3.
5.3. Receiver Section
At the receiver, the splitter splits the optical signal at the fiber output. The optical signal is passed through a band pass Bessel optical filter with FWHM of 40 GHz to filter out the required wavelength. The detection is done with
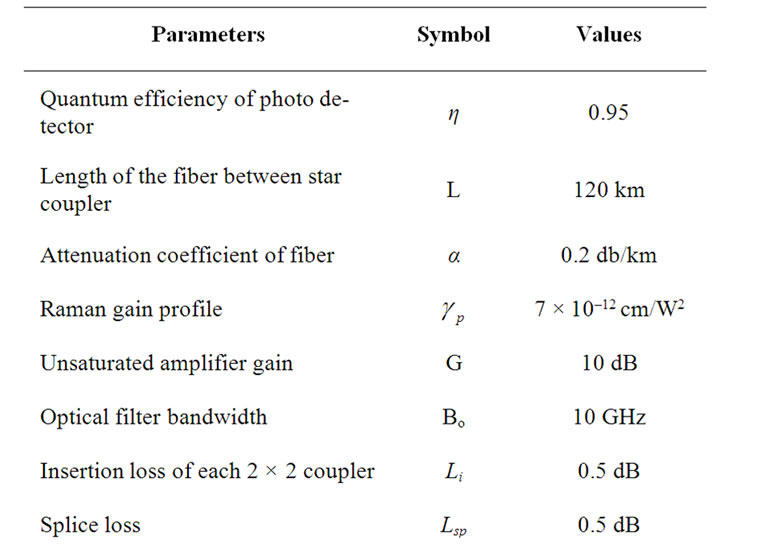

Table 1. Values of different parameters used in simulation.
the use of PIN photodiode which has a quantum efficiency of 0.95. Electrical filter of low pass Bessel type with 5 poles & –3 dB BW of 0.75 × Bit Rate gives the electrical signal at its output which is subsequently measured for Q values and eye diagram. OptSim provides a visualization tool called Scope which is an optical or electrical oscilloscope with numerous data processing options like Q estimation and BER estimation.
6. Numerical Results and Conclusions
With the parameters mentioned in Table 1, Q for different values of transmitted power has been computed for the worst affected channels when (a) thermal, shot and SRS noise (b) thermal, shot, FWM and SRS noise, and (c) thermal, shot, FWM, SRS and ASE noise are present. Figures 4 and 5 show the variation of Q with transmitted power on the worst affected channel due to SRS (i.e., 1st channel) with channel separation of 100 GHz and 50 GHz when the number of channels is 8 and 16 respectively. The variation of Q with transmitted power on the worst affected channels due to FWM (i.e., 5th channel when total number of users is 8 and 9th channel when total number of users is 16) with channel separation of 100 GHz and 50 GHz is shown in Figures 6 and 7 for 8 and 16 channels respectively.

Figure 4. Variation of Q-factor with transmitted power for the worst affected channel due to SRS for 8 channels with channel separation of 100 GHz and 50 GHz.
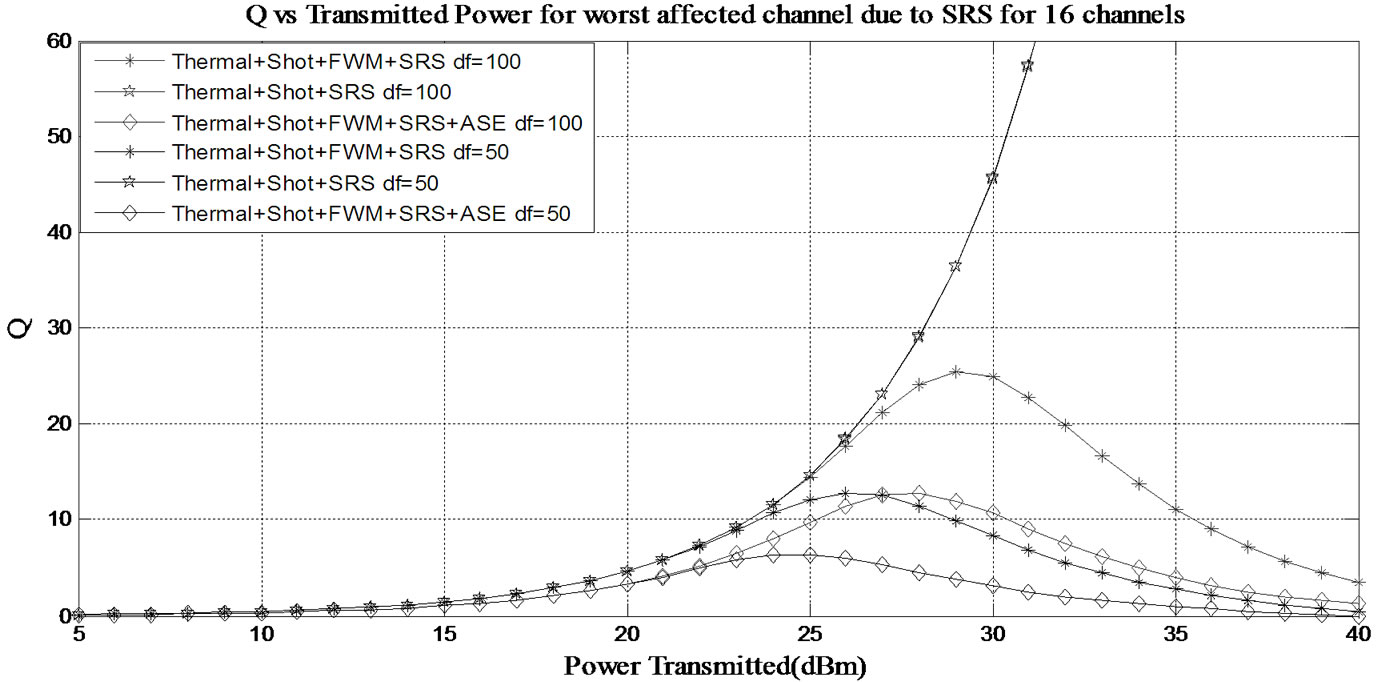
Figure 5. Variation of Q-factor with transmitted power for the worst affected channel due to SRS for 16 channels with channel separation of 100 GHz and 50 GHz.
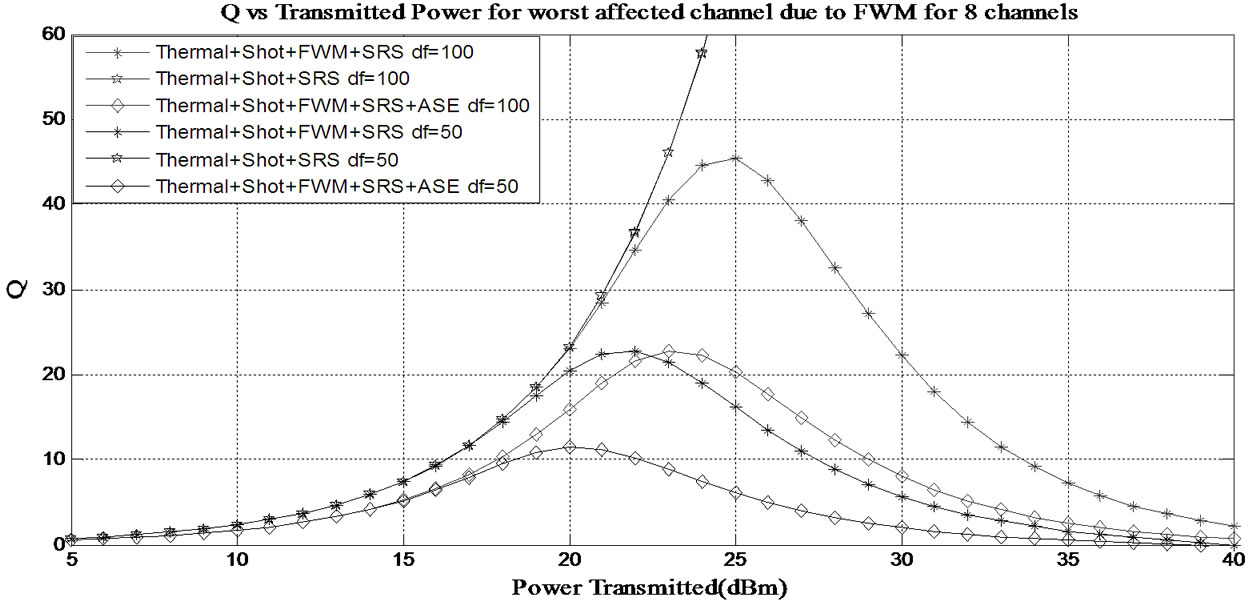
Figure 6.Variation of Q-factor with transmitted power for the worst affected channel due to FWM for 8 channels with channel separation of 100 GHz and 50 GHz.
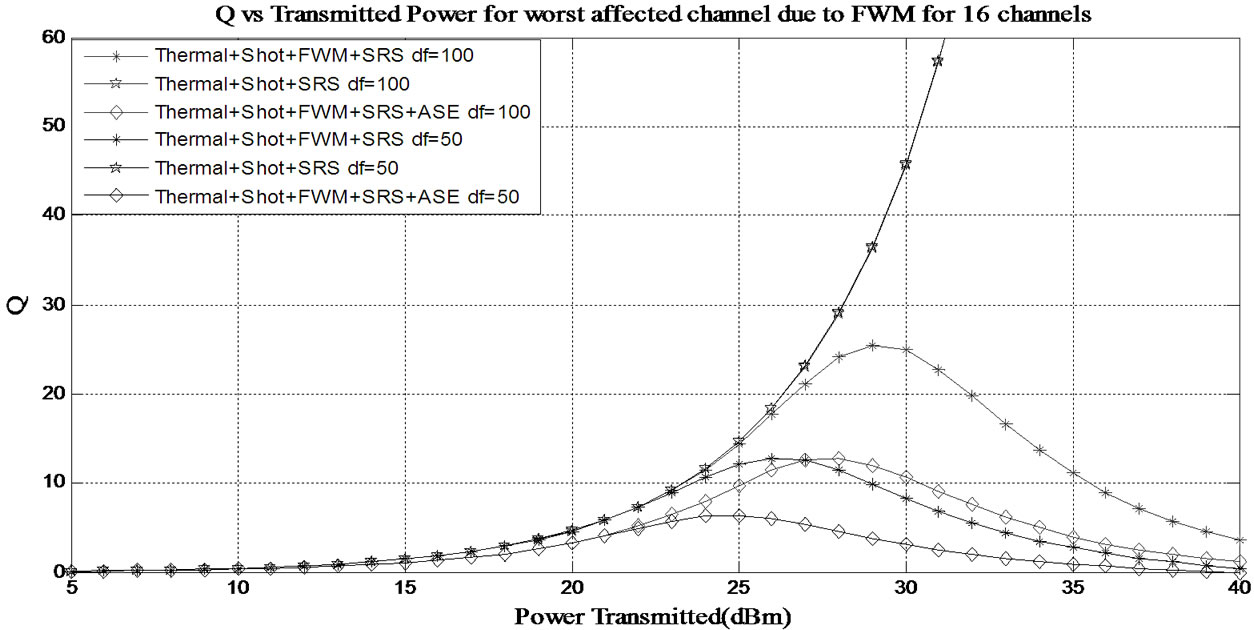
Figure 7. Variation of Q-factor with transmitted power for the worst affected channel due to FWM for 16 channels with channel separation of 100 GHz and 50 GHz.
It can be observed from these figures that in both the cases:
1) In presence of SRS, thermal and shot noises, Q increases linearly with the transmitted power irrespective of the channel separation.
2) In presence of FWM, SRS, shot and thermal noises, Q increases to a certain power level after which it starts decreasing as FWM noise is dominant at high power level.
3) In presence of ASE noise along with FWM, SRS, thermal and shot noises, the maximum value of Q further decreases for a given transmitted power.
4) Performance of the network when the frequency separation is 50 GHz is worst compared to when the separation is 100 GHz. This is due to the fact that as the channel separation decreases, the effect of FWM increases resulting in performance degradation.
In order to observe the effect of increase in number of channels on the performance of worst affected channels, we varied the number of channels while keeping the channel separation value constant. Variation of Q with transmitted power on the worst affected channel due to SRS with channel separation of 50 GHz and 100 GHz is presented in Figures 8 and 9 respectively. Similar variation on the worst affected channels due to FWM with channel separation of 50 GHz and 100 GHz is presented in Figures 10 and 11 respectively. It can be observed from the figures that on both the channels, the performance of a 16-channel network is worst compared to the performance when the number of channels is 8, irrespective of channel separation. This is due to the following reasons:
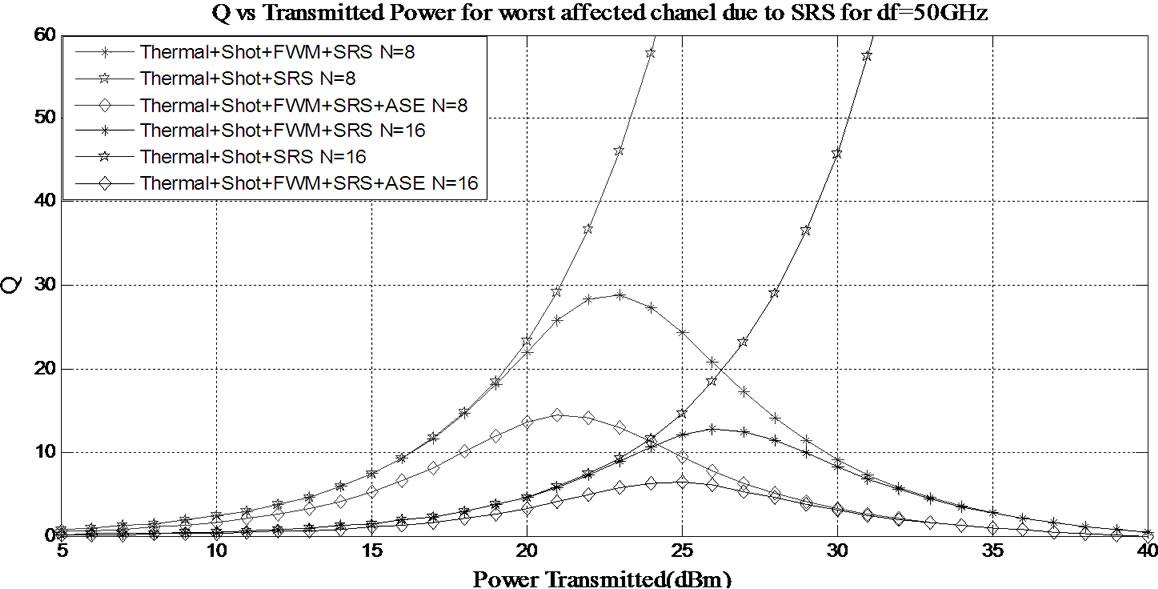
Figure 8. Variation of Q-factor with transmitted power for the worst affected channel due to SRS with 50 GHz channel separation when there are 8 and 16 channels.
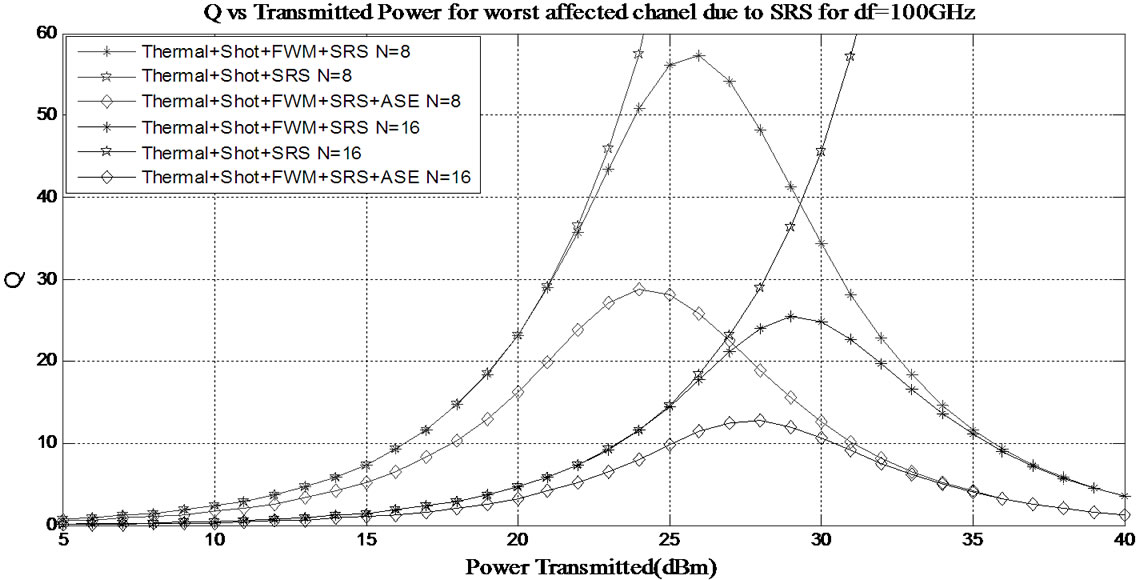
Figure 9. Variation of Q-factor with transmitted power for the worst affected channel due to SRS with 100 GHz channel separation when there are 8 and 16 channels.
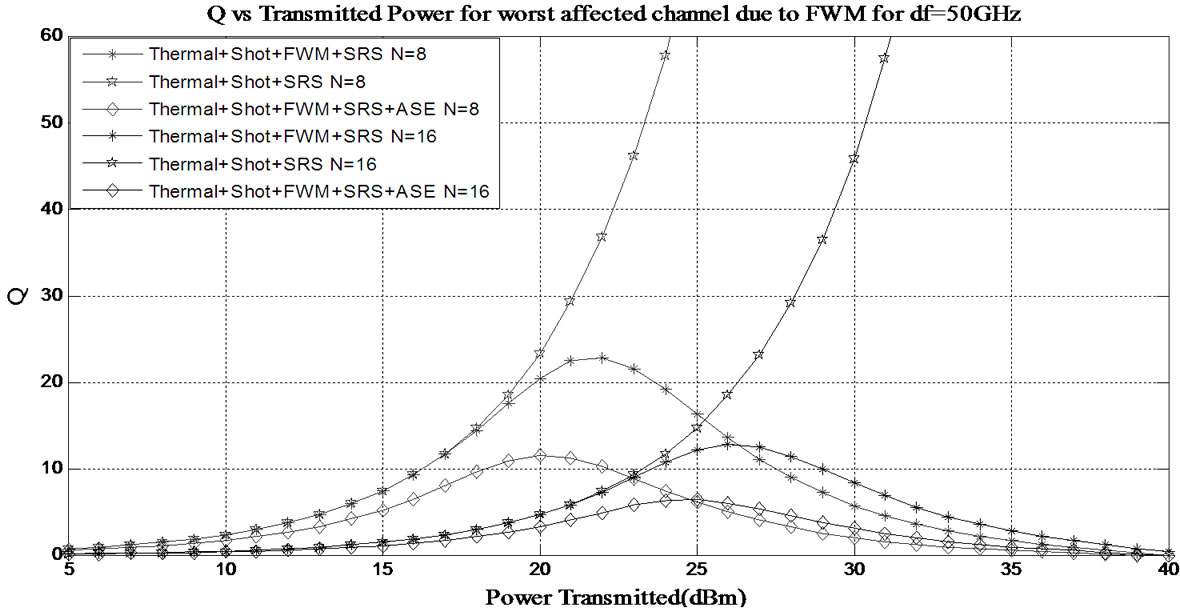
Figure 10. Variation of Q-factor with transmitted power for the worst affected channel due to FWM with 50 GHz channel separation when there are 8 and 16 channels.
1) With the increase in number of channels, power loss in the splitter increases as a result of which higher transmitted power is required to obtain a given value of Q.
2) With the increase in the number of channels, the number of FWM components generated increase leading to degraded network performance.
To validate the proposed theoretical model, simulation was performed on the network shown in Figure 3 using OptSim software, under the presence of all the noises (i.e. shot, thermal, SRS, FWM and ASE noise). Q vs transmitted power has been plotted for the worst affected channel due to SRS with frequency separation of 100 GHz and 50 GHz in Figure 12 for 8 and 16 channels respectively. Similarly, Q vs transmitted power on the worst affected channels due to FWM with frequency separation of 100 GHz and 50 GHz are shown in Figure 13 for 8 and 16 channels respectively.
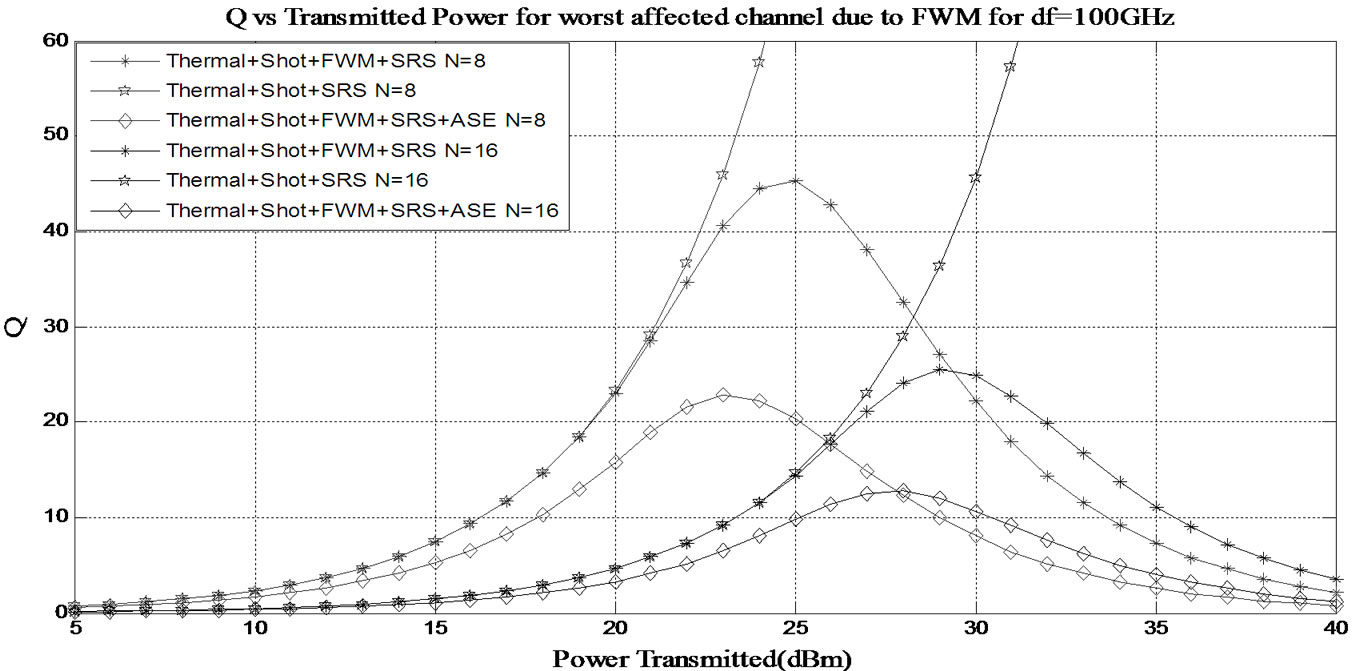
Figure 11. Variation of Q-factor with transmitted power for the worst affected channel due to FWM with 100 GHz channel separation when there are 8 and 16 channels.
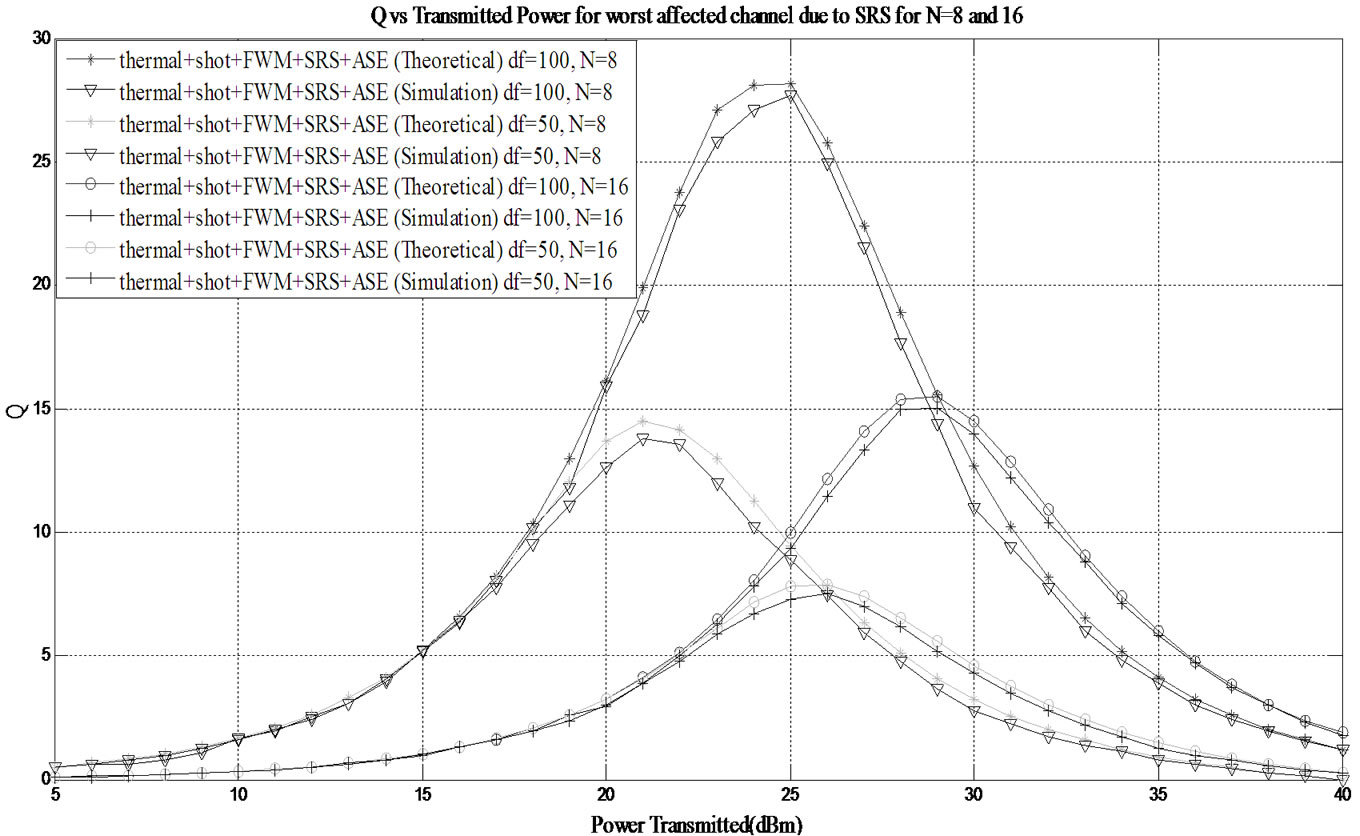
Figure 12. Comparison of theoretical and simulated results for variation of Q-factor with transmitted power for the worst affected channel due to SRS for 8 and 16 channels with channel separation of 100 GHz and 50 GHz respectively.
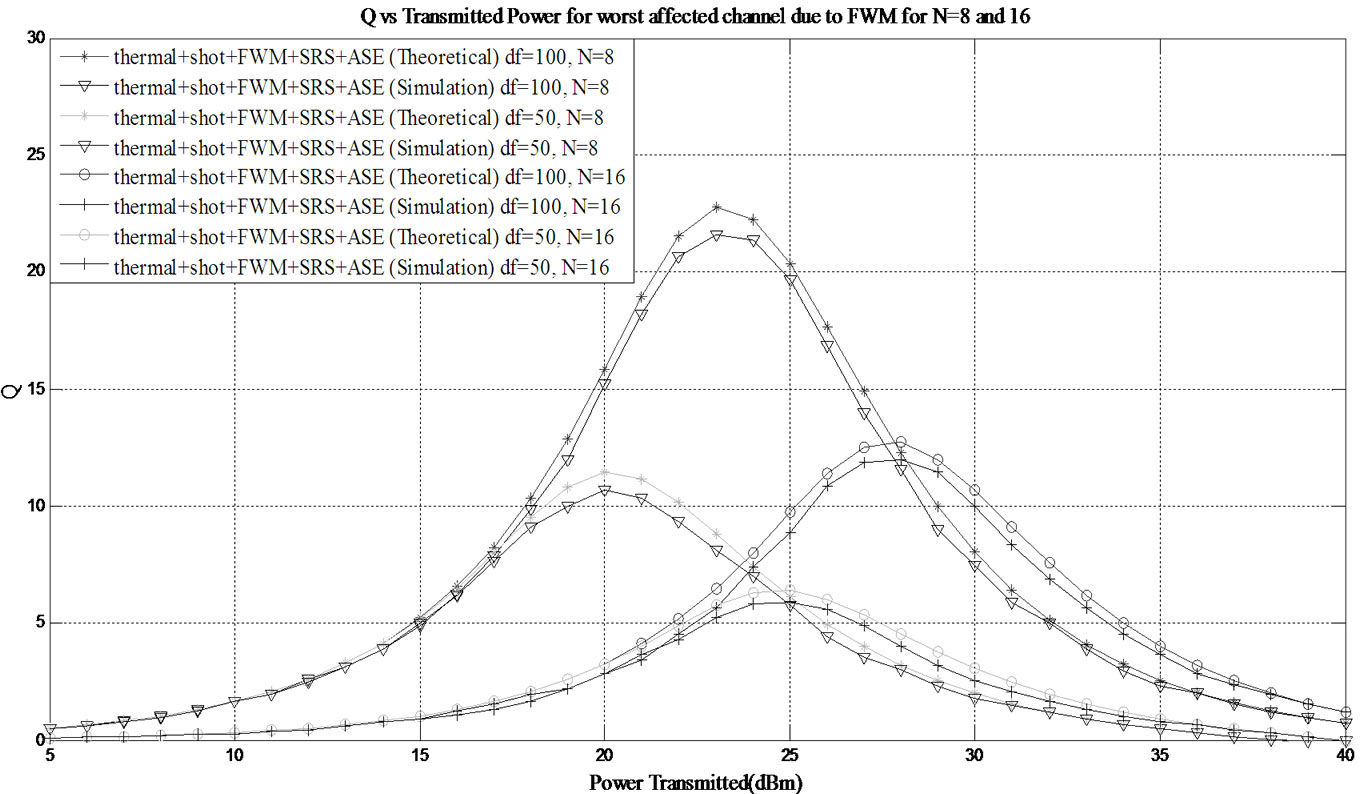
Figure 13. Comparison of theoretical and simulated results for variation of Q-factor with transmitted power for the worst affected channel due to FWM for 8 and 16 channels with channel separation of 100 GHz and 50 GHz respectively.
It can be observed from these figures that:
1) The OptSim results provide a degraded value of Q in comparison to the exact theoretical approach. This can be attributed to the fact that OptSim simulates the nonlinear fiber using Split Step Fourier technique (or Time Domain Split Step technique) which obtains an approximate solution to the Nonlinear Schrodinger equation (NLSE) that defines the pulse evolution inside a single mode fiber [21]. Even with the slight deviation in Q values; the graphs show that the simulation results follow the theoretical result which suggests that our model accurately calculates the Q-factor of the all optical WDM network.
2) When the number of channels is 8 or 16, the performance of the worst affected channel due to FWM is inferior compared to the performance of the worst affected channel due to SRS for either frequency separation. This can be attributed to the fact that on the 5th channel ( or the 9th channel), due to SRS, the power gain from lower wavelength channels is much lower in comparison to the power that is lost to the higher wavelength channels. Also, maximum FWM components are generated at the central channel. Thus, the higher power loss together with the dominant FWM effect leads to higher Q-factor degradation at the 5th channel (or the 9th channel) compared to the degradation at the 1st channel. Similar results can be observed from Tables 2-3 when the number of users is 8, and Tables 4-5 when the number of users is increased to 16. It can be seen from Table 2 that the maximum value of Q (theoretical) obtained on the 1st channel that is worst affected due to SRS is 28.12 (when Pt = 24 dBm, Δf = 100 GHz, N = 8) whereas it is 22.77 on the 5th channel which is worst affected due to FWM. When the number of channels is increased to 16, it can be observed from Table 4 that the maximum value of Q obtained on 1st and 9th channel decreases to 15.51 and 12.73 respectively.
3) It can be observed from Table 5 that with Δf = 50 GHz and N = 16, maximum value of Q (theoretical) obtained on the 9th channel is 6.39 (for Pt = 25 dBm). This suggests that if the number of users further increase or the channel separation decreases, it may not be possible to obtain an error rate of 10−9 (i.e., Q = 6).
Hence, it can be inferred that for a given number of channels there exists an optimum value of channel spacing to obtain the performance at error rate of 10−9 (i.e., Q = 6). Further, the above observations indicate that the performance of the central (i.e., jth) channel is worst compared to the 1st channel and thus for reliable transmission and improved overall system performance, the 1st channel must be preferred for transmission in comparison to the center channel.
To conclude, comparison of the worst affected channels due to SRS and FWM based on channel spacing and number of users indicates that the worst affected channel due to FWM gives degraded performance compared to the worst affected channel due to SRS. This comparison result suggests that the 1st channel should be preferred
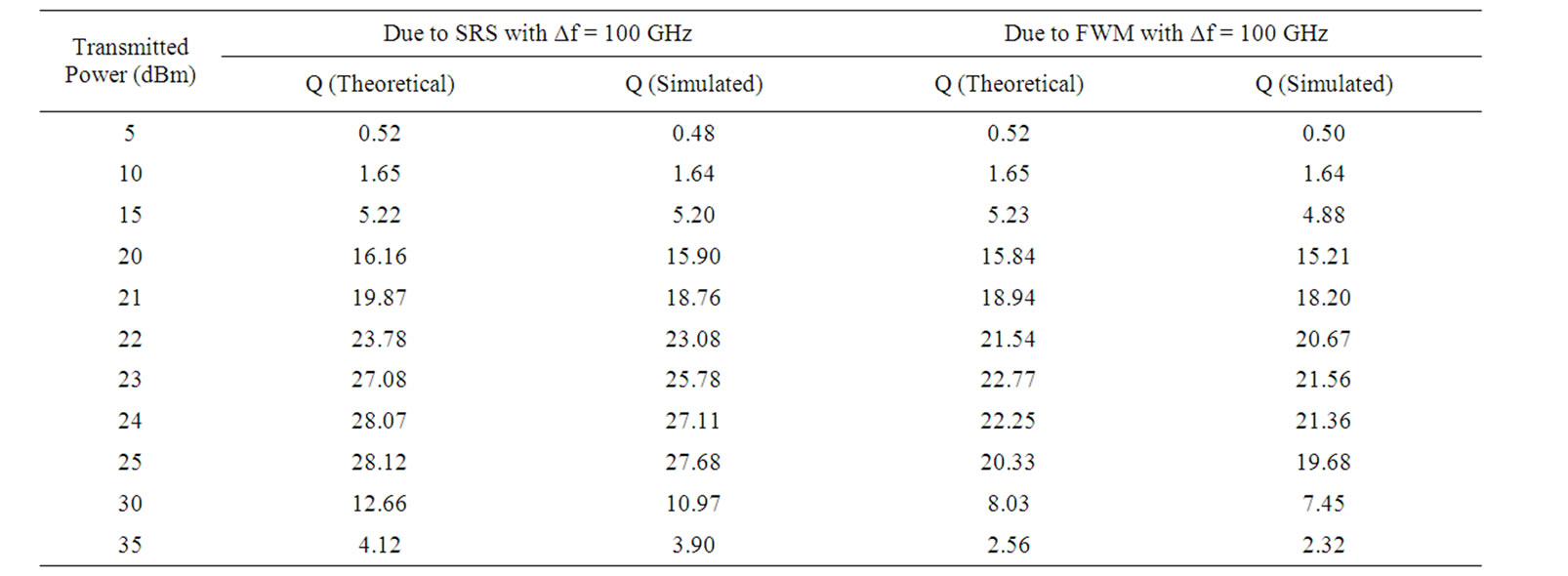
Table 2. Comparison of theoretical and simulated values for worst affected channel due to srs and fwm for N = 8.
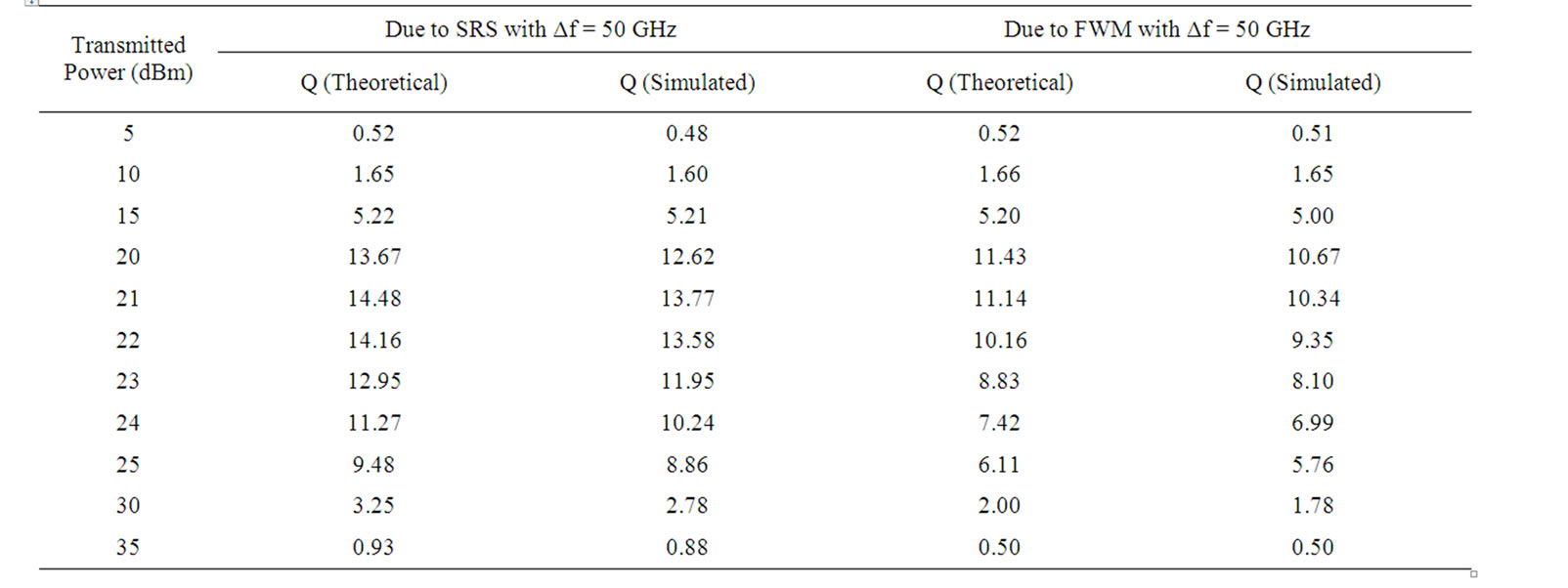
Table 3. Comparison of theoretical and simulated values for worst affected channel due to SRS and FWM for N = 8.
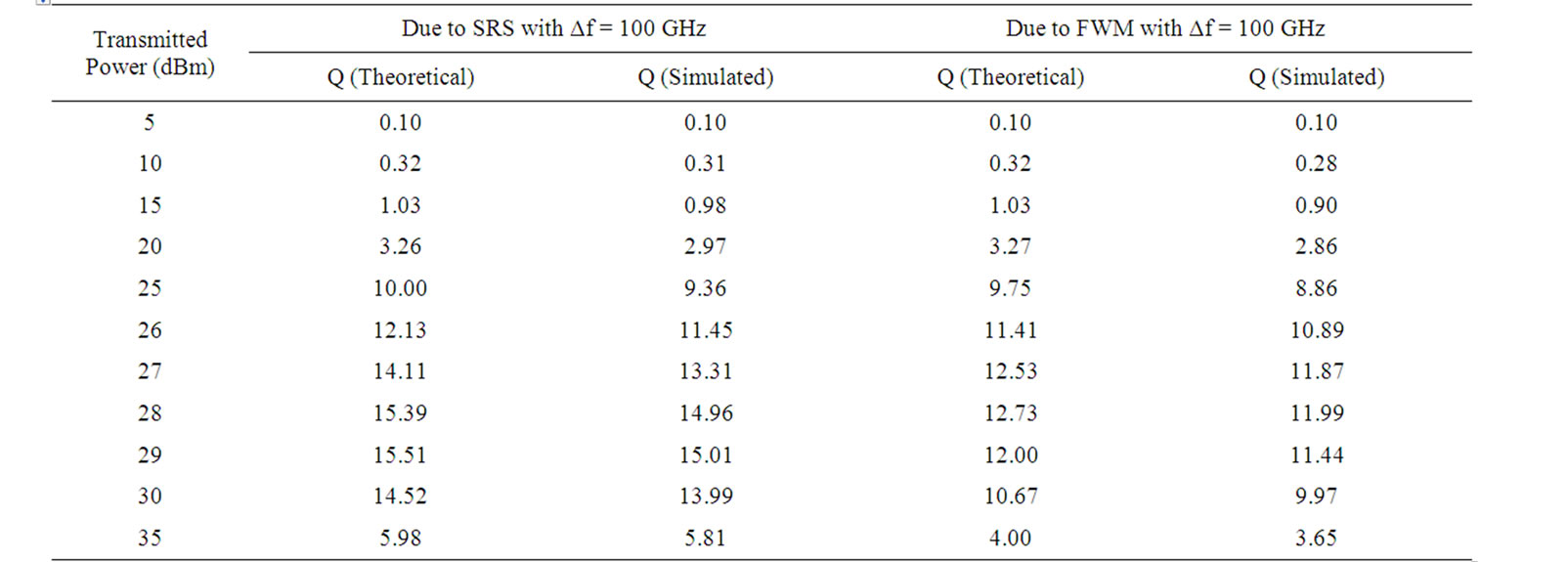
Table 4. Comparison of theoretical and simulated values for worst affected channel due to SRS and FWM for N = 16.
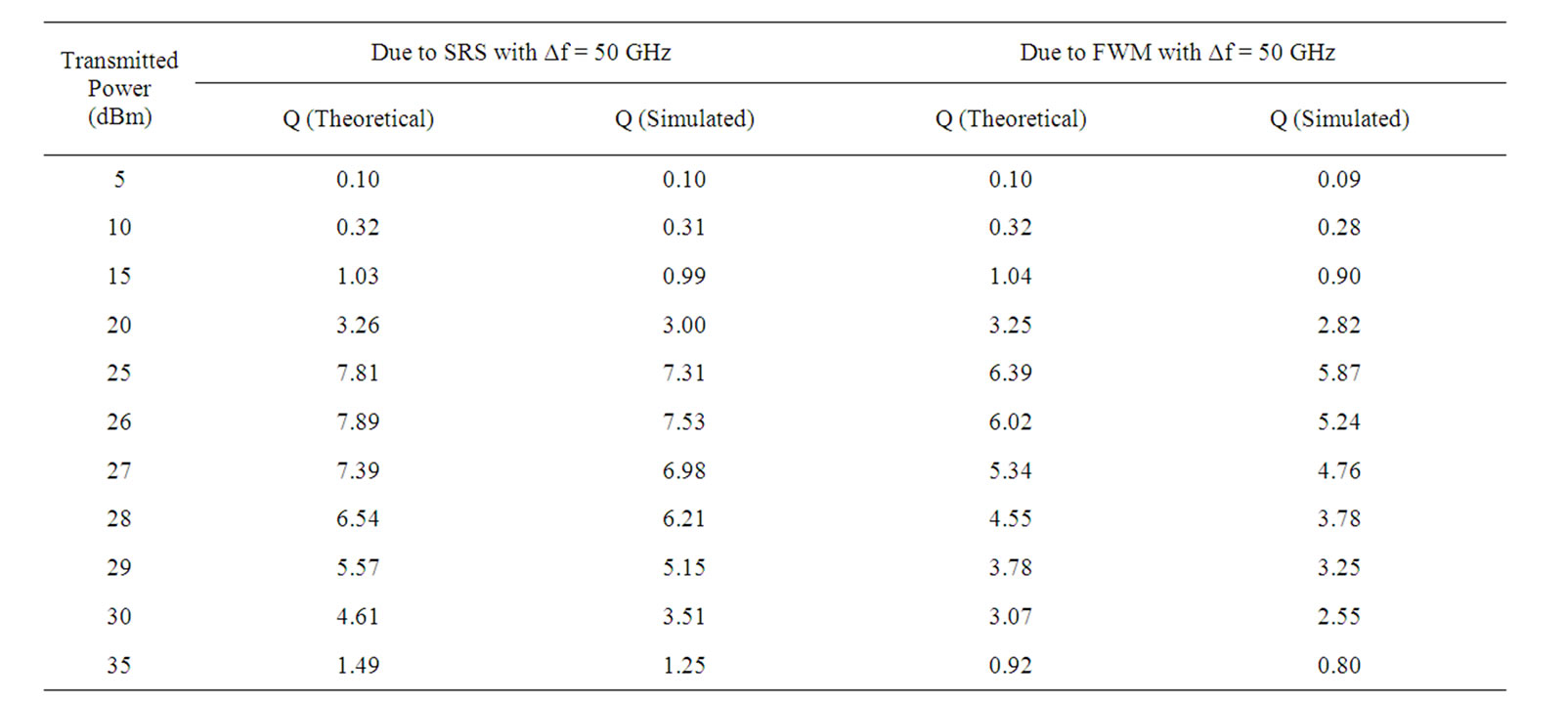
Table 5. Comparison of theoretical and simulated values for worst affected channel due to SRS and FWM for N = 16.
for transmission over the center channel (i.e., jth channel). The results obtained based on this investigation are applicable to all optical WDM networks of any length since FWM dominates over SRS with increase or decrease in the length of the fiber. Hence, performance of the worst affected channel due to FWM will always be inferior in comparison to the worst affected channel due to SRS.
7. Acknowledgements
The authors would like to thank the AICTE for funding this work under research promotion scheme (RPS-11/ 2008-09). Authors are also thankful to Prof. Subrat Kar, Department of Electrical Engineering, IIT Delhi and Ms. Sujata Sengar, Division of Electronics and Communication Engineering, NSIT, New Delhi for giving valuable suggestions and comments.
[1] B. Mukherjee, “WDM-Based Local Lightwave Networks Part-1: Single-Hop Systems,” IEEE Network, Vol. 6, No. 3, 1992, pp. 12-27. doi:10.1109/65.139139
[2] D. Marcuse, A. R. Chraplyvy and R. Tkach, “Effect of Fiber Nonlinearity on Long-Distance Transmission,” Journal of Lightwave Technology, Vol. 9, No. 1, 1991, pp. 121-128. doi:10.1109/50.64931
[3] G. P. Agrawal, “Fiber-Optic Communication Systems,” 3rd Edition, John Wiley & Sons, Hoboken, 2002. doi:10.1002/0471221147
[4] F. Forghieri, R. W. Tkach and A. R. Chraplyvy, “Optical Fiber Telecommunications (IIIA)―Fiber Nonlinearities and Their Impact on Transmission Systems,” Academic Press, San Diego, 1997, pp. 196-264.
[5] J. Villarroel and A. G. Grandpierre, “On Statistical Effects on Stimulated Raman Cross-Talk,” Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 38, 2005, pp. 2601-2612. doi:10.1088/0953-4075/38/15/002
[6] I. B. Djordjevic and A. Stavdas, “Analytical Modeling of Stimulated Raman Scattering in WDM Systems with Dispersion Compensated Links,” Journal of Optical Communication, Vol. 24, No. 2, 2003, pp. 54-60.
[7] S. Norimatsu and T. Yamamoto, “Waveform Distortion Due to Stimulated Raman Scattering in Wide-Band WDM Transmission Systems,” Journal of Lightwave Technology, Vol. 21, No. 2, 2001, pp. 2172-2181. doi:10.1109/50.917870
[8] K. P. Ho, “Statistical Properties of Stimulated Raman Crosstalk in WDM Systems,” Journal of Lightwave Technology, Vol. 18, No. 7, 2000, pp. 915-921. doi:10.1109/50.850735
[9] A. V. T. Cartaxo, “XPM in IM/DD WDM System with Multiple Optical Amplifiers and Dispersion Compensators,” Journal of Lightwave Technology, Vol. 17, No. 2, 1999, pp. 178-190. doi:10.1109/50.744218
[10] F. Zhang, “XPM Statistics in 100% Precompensated WDM Transmission for OOK and DPSK Formats,” IEEE Photonics Technology Letters, Vol. 21, No. 22, 2009, pp. 1707-1709. doi:10.1109/LPT.2009.2032069
[11] M. Eiselt, “Limits on WDM Systems Due to Four-Wave Mixing: A Statistical Approach,” Journal of Lightwave Technology, Vol. 17, No. 11, 1999, pp. 2261-2267. doi:10.1109/50.803018
[12] V. Mikhailov, C. R. Doerr, S. Appathurai, R. I. Killey and P. Bayvel, “Fiber Nonlinearity and Dispersion Mitigation in 40-Gb/s NRZ WDM Transmission Using a Multichannel Optical Equalize,” IEEE Photonics Technology Letters, Vol. 18, No. 2, 2006, pp. 376-378. doi:10.1109/LPT.2005.861965
[13] I. B. Djordjevic, “Transmission Limitations of WDM Transmission Systems with Dispersion Compensated Links in the Presence of Fiber Nonlinearities,” Proceeding of 5th International Conference on Telecommunications in Modern Satellite, Cable and Broadcasting Service, TELSIKS, IEEE, Nis, Yugoslavia, Vol. 2, September 2001, pp. 496-499. doi:10.1109/TELSKS.2001.955826
[14] A. Yu and M. J. O’Mahony, “Optimization of Wavelength Spacing in a WDM Transmission System in the Presence of Fiber Nonlinearities,” IEE Proceedings of Optoelectronics, Vol. 142, No. 4, 1995, pp. 190-196. doi:10.1049/ip-opt:19952070
[15] S. Tariq and M. K. Dhodhi, “Limits of DWDM Communication Networks Due to Stimulated Raman Scattering and Optical Amplifier Noise,” The Eleventh International Conference on Microelectronics (ICM 1999), November 1999, pp. 189-191. doi:10.1109/ICM.2000.884837
[16] S. P. Singh, S. Kar and V. K. Jain, “Effect of Four Wave Mixing on Optimal Placement of Optical Amplifier in WDM Star Networks,” Fiber & Integrated Optics, Vol. 25, 2006, pp. 111-140. doi:10.1080/01468030500466289
[17] S. P. Singh, S. Kar and V. K. Jain, “Performance of AllOptical WDM Network in Presence of Four-Wave Mixing, Optical Amplifier Noise, and Wavelength Converter Noise,” Fiber & Integrated Optics, Vol. 26, No. 2, 2007, pp. 79-97. doi:10.1080/01468030601131477
[18] S. P. Singh and Sridhar Iyer, “Impact of SRS and FWM on Performance of Optical Star WDM Networks,” Symposium on Photonics and Optoelectronics (SOPO 2011), May 2011, pp. 1-4. doi:10.1109/SOPO.2011.5780620
[19] ITU-T Recommendation G.692, “Optical Interfaces for Multichannel Systems with Optical Amplifiers,” 1997.
[20] ITU-T Recommendation G.653, “Characteristics of a Non-Zero Dispersion Shifted Single-Mode Optical Fiber Cable,” 1996.
[21] G. P. Agrawal, “Nonlinear Fiber Optics,” 3rd Edition, Academic Press, New York, 2001.