An Integrated Optimal Approach for Solar Powered Rural Water Distribution Systems in the Gambia ()
1. Introduction
Rural water supply in sub-Saharan Africa is largely ineffectual. Sustainable Development Goal 6.1 aims to “by 2030, achieve universal and equitable access to safe and affordable drinking water for all”. However, only 58% of the region’s population uses at least a basic drinking water service, defined by the WHO/UNICEF Joint Monitoring Programme as no more than a 30 minute round trip to collect water from an improved source [1] . Access to water is essential for meaningful and holistic development, and influences health, education, gender equality, livelihoods and environment, among other areas. Lack of progress towards this in rural sub-Saharan Africa is compounded by broader trends such as population growth, urbanisation, economic inequality and poverty, along with increasing environmental pressures on water resources such as climate change and pollution [2] [3] [4] [5] . Even in communities that benefit from piped water to communal standpipes from a central borehole and storage tank, water distribution systems often fail or perform sub-optimally. It is suggested that rural water supply should provide 50 litres of water per capita per day [6] .
Part of this challenge is sufficient provision of electricity supply required for pumping water from the aquifer. This is a particular problem in rural sub-Saharan Africa where grid supply is limited. Here, sources of off-grid sustainable electricity were reviewed and solar was concluded to be most reliable and appropriate. Variation in available power can be negated by using an elevated water storage tank that distributes water with gravity and re-fills when solar power is available. This research brings together work done on modelling and optimisation of water distribution networks and modelling of energy yielded through solar power.
2. Methodology, Scenarios and Modelling
A water distribution network model utilising groundwater and solar photovoltaics (PV), which is capable of supplying 50 litres of water per capita to standpipes within 100 m of residences, will be investigated. The village of Jarreng in the Gambia (13˚37'24"N 15˚11'28"W; population 2800) was selected as a basis for the study as shown in Figure 1(a) and Figure 1(b).
Extracted water is stored in an elevated tank, providing a pressure head for distribution through a pipe network to standpipes. The challenges of this type of system, and methods for mitigating them, will be investigated using a combination
![]()
Figure 1. (a) Jarreng Village satellite image, and (b) Jarreng Village with contour lines of 10 m elevation. Source: Google Earth.
of techniques for modelling solar energy and water distribution networks. Currently, a solar powered water distribution system has been installed to supply 28 standpipes from a central borehole. Figure 2(a) and Figure 2(b) outline the system’s predicted daily and hourly water yields based on solar power capacity. The system consists of:
・ Water source: 90 m deep, 6 inch diameter borehole with static water level (SWL) of 13 m;
・ Pump: submersible centrifugal pump;
・ Energy Source: 3.9 kilowatt peak solar array, containing 26 solar photovoltaic modules of 150 Wp each;
・ Storage Tank: 60 m3 capacity, 3.4 m depth, 6.3 m above ground level;
・ Pipe Network: Polyvinyl Chloride (PVC) piping: 90 mm, 63 mm, 50 mm, and 40 mm diameters.
In order to meet the requirement for 50 litres of water per capita per day [6] , each day a total of 140 m3 is required for the population of 2800. As shown in Figure 2(a), currently the quantities of water being pumped range between 104 m3 and 140 m3. Figure 2(a) shows that March is the only month with enough power from the solar array to pump water sufficient to supply 50 litres of water per capita per day to the population.
![]()
![]()
Figure 2. (a) Predicted daily water yields per month, and (b) hourly water yields. Source: GAM-Solar Energy Banjul.
2.1. EPANET System Modelling
EPANET was used to model the water distribution system.
Node location: A series of aerial images of Jarreng were extracted from Google Earth at a consistent scale and stitched together in image editing software (GIMP) [7] . This high-definition aerial image was then imported into EPANET and the network model scale was set to coincide with the image scale. A series of 100 m diameter circles were overlaid on the image, the centre of each indicating a standpipe model node, and ensuring that every property is within 100 m of a node, as shown in Figure 3.
Pipe Network Configuration: Looped networks (shown in Figure 4) are preferable to dentritic (branched) networks (shown in Figure 5) because, with appropriate use of valves, they allow for isolation and maintenance on pipes without disrupted service. Looped networks, however, require more pipework and therefore cost [8] .
Diameters and roughness factors were assigned to pipes in the two configurations. Pipework default diameter of 150 mm was chosen, and for the PVC material
![]()
Figure 3. Node locations on aerial map image of Jarreng.
![]()
Figure 4. Looped network layout configuration.
the Hazen-Williams pipe head-loss equation was selected, thus giving a head-loss factor of 150 applied to each pipe [9] .
2.2. Solar Modelling
Factors that influence power output of solar photovoltaic arrays are: geographical position; direction and slope; area and efficiency of PV panels; time of day; and seasonal solar variation. The power output of the array influences volumes of pumped water based on: pump efficiency, hydraulic head that needs to be overcome to the storage tank and power loss in electrical components. Here, the solar array is taken to be facing towards the equator and to have a tilt angle that equals the latitude, for the consistency of calculations. Maps of solar irradiation based on aggregated local measurements and statistical analyses are used. Efficiency of the solar array is a function of irradiation, cell temperature and the relative air mass. Air mass and irradiance can both be estimated from the latitude of a location and the day of the year, but an estimated average annual temperature was used as the parameter, meaning values for summer and winter yields could be overestimated and underestimated.
2.3. Scenarios
A series of scenarios was created with which to test the network and fulfil demands upon it. Cost implications of the looped and dendritic networks that were mapped in Figure 4 and Figure 5 were investigated to understand the cost of building in the redundancy potential that looped networks provide.
Demand scenarios: Assuming a population of 2800 and that the requirement of 50 litres per person per day is fulfiled, four different demand curves were created in EPANET to simulate peaks in water demand occurring for different points in the day (7 am, 12 pm, 5 pm and a dual peak of 7 am with 5 pm) as shown in Figure 6. Baseline demand rate for Jarreng is calculated as below:
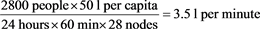
![]()
Figure 6. Simulated demand curves for the four demand scenarios.
Supply scenarios: Water supply from pumping is dependent on available solar energy. This depends on PV panel area and efficiency. Available power via the solar array also varies seasonally with day length and solar incidence angle variation. Rate of flow into the storage tank is dependent on available solar power, pressure head and flow rate of the pump. To calculate an estimate of available supply, indicative days for solar radiation in Jarreng were calculated for each month [10] . Latitude and annual average solar radiation were combined to estimate the relationship between time of day and available solar irradiance. Theoretical hourly solar irradiation values for the months of January and July are reported in Figure 7 as the months at either end of this range. July and January were chosen as examples to demonstrate changing solar irradiance throughout the year. The total theoretical annual yield for a site at latitude 13.623 (13˚37'24") is calculated to be 2677 kWh/m2 [10] . Actual average solar radiation for the Gambia is reported to be 2100 kWh/m2 (https://solargis.com/). This lower value is unsurprising due to atmospheric particulate matter and other irradiance inhibition. The modified figure for irradiance is therefore 784 W/m2.
Using the calculated solar irradiance values, the efficiency of solar energy converted to electrical power per m2 of PV array at an average temperature in Jarreng of 28˚C was calculated, and reported in Table 1.
These electrical power values indicate the potential volume of water that could potentially be pumped, which allows the minimum solar panel area required. The minimum area is the area that would be sufficient to power the pump in December so that it delivers enough water to the water storage tank, December being the month with the lowest output (Table 1). This required using the reported pump curves for the pump mentioned above for eight different heights from aquifer to tank (10 m to 45 m). Pump curves calculated from these theoretical electric power values were plotted against the reported pump curves for the pump system, and conformed closely with the reported pump curves with high R2 values (0.983 - 0.999). Higher and lower kW values tend to marginally overestimate and underestimate respectively, however, and were treated with caution.
![]()
Figure 7. Variation in theoretical hourly solar irradiance on a surface sloped at the angle of latitude for Jarreng on indicative days in January and July.
![]()
Table 1. Average photovoltaic output per month.
As discussed, because December has the minimum theoretical solar output (Table 1), output of the solar array on the indicative day for December (the 10th) should be the basis for sizing. 140 m3 is the minimum volume required, as discussed above. The pressure head that must be overcome by the pump was assessed to calculate the sizing of a sufficient solar array. Pump output figures at the eight different pump heads (elevations) of 10 m to 45 m over a day for a 15 m2 array in December were calculated and reported in Table 2. This array area of 15 m3 is found to be sufficient to satisfy the water supply of 140 m3 required per day if the head is 10 m (it provides a volume of 153.1 m3), but drops to 121.4 m3 at 15 m. Therefore, elevations higher than 10 m require a larger solar array area.
![]()
Table 2. Pump rates on the indicative day for December (10th) supplied by a 15 m2 solar array.
2.4. Storage Tank Sizing
Volume and elevation of the storage tank are investigated. Volume must be adequate to meet demand at times when pumped supply is insufficient. Elevation will need to provide enough head to ensure flow to every standpipe. The elevation of the tank will have an impact on the size of the solar array due to the pump requiring more power to overcome the difference in head between the static water line of the ground water and the top of the water storage tank. The higher the tank, the greater the hydrostatic pressure head generated (as a product of density of water, gravitational acceleration and height difference between tank and node). The static water level of the borehole in Jarreng is 13 m below ground level therefore the pump will need to overcome a pressure head of the tank height plus 13 m; another 2 m was also subtracted from the pumps pressure head to allow for frictional losses between the pump and the tank.
A safety factor is applied to the minimum daily volume of 140 m3 required, to encompass inaccuracies. 180 m3 was chosen as a safe volume to use. The area of the photovoltaic panel for eight different pressure heads that is required to supply >180 m3 of water were calculated, along with hourly flow rates these array sizes would provide. They are reported in Table 3. Tank heights of 5 m, 10 m and 15 m were selected as tank heights to be modelled in EPANET, as below.
The required tank volumes were calculated by comparing the outgoing demands on the water storage volume with the incoming pumped supply. When demand exceeds supply the shortfall is met by remaining storage. When supply exceeds demand the storage is replenished. This is illustrated using the morning
![]()
Table 3. Required solar array sizes to deliver >180 m3 at different pressure heads.
peak demand profile (as discussed) in Figure 8.
The required storage volumes for each demand profile on December 10th were therefore calculated as follows: Dual Peak 70 m3; Morning Peak 52 m3; Noon Peak 20 m3; Afternoon Peak 73 m3. The location of the storage tank was taken as the average of the x- and y-coordinates of all the nodes. The supply multipliers were renamed Water Input (5 m), Water Input (10 m), and Water Input (15 m) to coincide with the flow rates calculated for each storage tank height, and concomitant array size. Storage volumes were entered into EPANET as a diameter, maximum level, minimum level, elevation and initial level. For each EPANET model the maximum level was set to 3 m and the minimum level to 0 m, the diameter was then set to provide the requisite volume. Once the models were loaded into EPANET, the initial level was adjusted down until it coincided with the level after a 24 hour period to ensure that the volume was functional.
2.5. Model Output
The model was successfully run using December’s indicative day (10th) pump output and a tank elevation of 5 m, in conjunction with each of the four demand scenarios and their calculated tank volumes. Figure 9 reports the modelled tank level with these parameters for the looped network with the duel peak demand.
3. Genetic Algorithm Optimisation
The models were then optimised in terms of the lowest cost network system that would fulfil the requirements of: 1) meeting the demands for water at each node, and 2) maintaining a pressure head at each node that is greater than a set minimum throughout a 24 hour period. Objectives chosen were to: 1) maximise average pressure head across all nodes, and 2) minimise overall cost.
Genetic algorithms were chosen for the optimization because the number of possible permutations is impractically large for conventional optimisation. Genetic algorithms are a type of stochastic optimisation technique that runs
![]()
Figure 8. The relationship between supply, demand and required storage volume for morning peak demand profile.
![]()
Figure 9. Tank level for the looped network running on the dual peak demand scenario from EPANET.
through a series of randomly generated iterations, each time selecting the solutions with the “best fit” to “survive” into the next iteration [11] .
The parameter used for the optimisation was the internal diameter of commercially available pipes. A cost relationship between installation of 1 m of pipe and pipe diameter was established using:
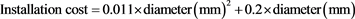 .
.
Calculated pipe costs per diameter are reported in Table 4.
The tool GANET [12] was chosen to run a multi-objective optimisation that uses a non-dominated sorting genetic algorithm with: population size 100, generations 300, simple one point crossover type at a rate of 0.85, a crowded tournament selector, and simple mutator with a mutation rate of 0.03. An infeasibility that multiplied total nodes with a pressure head below 2 m by 106 was included so the algorithm would dispense with solutions that failed to meet minimum pressure requirements. Twelve optimisations were run (beginning with a tank elevation of 5 m) in eight combinations of the four demand profiles and two network configurations. Optimal solutions for one example scenario are plotted in Figure 10. Here, a Pareto curve is demonstrated where there are a number of possible optimal solutions. Higher average nodal heads are possible at higher cost.
Eight scenarios were run using varying combinations of dendritic and looped
![]()
Figure 10. Genetic algorithm optimisation of dendritic network with 5 m elevation water tank and afternoon peak profile.
systems and morning, noon, afternoon and duel peak demand profiles, all for a tank height of 5 m, as outlined in Table 5. Cost and average nodal heads are reported.
Dendritic morning peak scenario and looped noon peak scenario were tested with tank elevations of 10 m and 15 m, reported in Table 6.
4. Discussion and Further Work
Table 5 and Table 6 show that, as expected, the looped network is more expensive than the dendritic network. The cost ratio for using a looped network over a dendritic network ranges between 156% for the morning peak demand profile, and 227% for the dual peak demand scenario, excluding additional valve and control appliance costs. By raising the tank elevation from 5 m to 10 m the cost
![]()
Table 5. Optimised cost and average nodal heads for the eight scenarios.
![]()
Table 6. Optimised cost and average nodal heads for four additional scenarios with greater tank heights.
of the dendritic network with morning peak demand profile can be reduced by 23,382 GBP. For a looped network with noon peak demand this reduction is 38,975 GBP. If the cost of higher tank elevation and larger solar are cheaper than these costs then overall cost can be reduced. If tank height for these two scenarios is raised by a further 5 m from 10 m, up to 15 m, then cost reduces by 3721 GBP and 3319 GBP respectively.
Demand profile variation has a large effect on network cost. The difference between a dendritic network configuration meeting the more costly morning peak demand and the cheaper dual peak demand is 18,403 GBP or 49.5% of the cheaper network (Table 5).
A cost benefit analysis that includes public health gains, lifespan of the system against likelihood of failure, maintenance speed and population is required for a conclusive preference. Better understanding of demand profiles across the day for specific locations would significantly enhance optimisation. This could be conducted by direct surveying of usage, or estimated using generalised proxies from secondary water consumption data. Supplying power and therefore pumping water throughout the night using battery power storage could allow for a reduced tank volume. Additionally, maintaining a full tank throughout the day using battery power would maintain a maximum pressure head during peak demand, however this must be reconciled with regular flushing of the tank for water quality concerns.
Here, solar radiation calculations did not include diffused irradiance from atmospheric scattering and reflected irradiance. Modelling methods for these require locally observed coefficients [13] . Likewise, solar cell temperatures exceed ambient temperature because solar energy conversion to thermal energy is not included [12] .
5. Conclusions
The potential of certain optimisations to rural water distribution systems in the Gambia is outlined and quantified here by using the case study of Jarreng. Lessons from here will be generally applicable to other systems in the Gambia and across sub-Saharan Africa. Looped networks are more expensive but offer enhanced resilience. Elevating a tank can significantly reduce network costs so long as the additional expenditure of raising the tank and providing the larger solar arrays required to pump water to the higher level do not exceed this. With this in mind, an elevation from 5 m to 10 m is likely to be more cost-beneficial than an elevation of 10 m to 15 m. Quantifiable benefits must be balanced with other potential cost implications and challenges of building tanks at higher elevations. Such costs will vary between settings, and this highlights the importance of considering rural water distribution systems within the complex operating system of rural water supply in sub-Saharan Africa.
A system designed for morning-peak demands can be 50% more expensive than for a dual-peak demand. This emphasizes the need for understanding demand profiles of communities when designing such water distribution systems. Engineering solutions alone are not sufficient. These conclusions have direct relevance to decision makers and planners who are aiming to reduce cost of rural water supply service delivery.
Acknowledgements
Thanks to eWATERpay (www.ewaterpay.com) and Rob Hygate.