Depolarization Effects of Incoherently Scattered Electromagnetic Waves by Inhomogeneous Magnetized Plasma Slab ()
1. Introduction
At the present time the features of light propagation in random media have been very well studied [1]. Atmospheric turbulence has a significant influence on radio wave propagation in the atmosphere causing fluctuations of the key parameters of the wave. Analysis of the statistical moments of small-amplitude electromagnetic waves scattered by turbulent anisotropic plasma slab is very important in many practical applications associated with both natural and laboratory plasmas. Angular power spectrum, scintillation effects and the angle-of-arrival of scattered electromagnetic waves by turbulent anisotropic magnetized ionospheric plasma slab for both power-law and anisotropic Gaussian correlation functions of electron density fluctuations were investigated analytically and numerically in [2-4]. Statistical characteristics of the amplitude and phase of scattered radiation by turbulent magnetized plasma slab with electron density and magnetic field fluctuations via the perturbation method were analyzed in [5]; phase portraits of the amplitude and phase correlation functions have been also constructed.
Electric field components of the scattered electromagnetic waves by magnetized plasma slab and second order statistical moments for arbitrary correlation function of electron density fluctuations are obtained. The results are valid for near and far zones with respect to plasma slab boundaries. Depolarization of the ordinary and extraordinary waves scattered by turbulent magnetized plasma slab and normalized variance of the Faraday angle 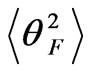 are investigated in this paper analytically by the perturbation method and numerically using the anisotropic Gaussian fluctuation spectrum.
are investigated in this paper analytically by the perturbation method and numerically using the anisotropic Gaussian fluctuation spectrum.
2. Formulation of the Problem
Let us consider electromagnetic waves scattering by plasma slab having finite thickness L. If the frequency of an incident wave satisfies the condition  , the ions can be considered immovable and only motion of electrons can be taken into account;
, the ions can be considered immovable and only motion of electrons can be taken into account; 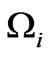 is the ion gyrofrequency, e is the electron charge,
is the ion gyrofrequency, e is the electron charge,  is the strength of the external magnetic field, M is the mass of an ion and c is the speed of light in vacuum. If
is the strength of the external magnetic field, M is the mass of an ion and c is the speed of light in vacuum. If ,
,  is the effective electron collision frequency with the ions and molecules, conduction current can be neglected and the total current in the medium equals to the displacement current
is the effective electron collision frequency with the ions and molecules, conduction current can be neglected and the total current in the medium equals to the displacement current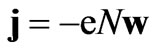 , where w is the velocity of electrons, N is the electron density in magnetized plasma. If the fields have timeharmonic dependence
, where w is the velocity of electrons, N is the electron density in magnetized plasma. If the fields have timeharmonic dependence , wave equation for electric field strength E can be written as [5]:
, wave equation for electric field strength E can be written as [5]:
 . (1)
. (1)
Taken into account that , (1) can be written as:
, (1) can be written as:
 (2)
(2)
where: ,
, 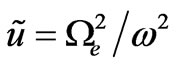 ,
,  ,
,  being the electron plasma frequency,
being the electron plasma frequency,
 is the electron gyrofrequency. For homogeneous gyrotropic medium without fluctuating plasma parameters (2) takes the tensor form:
is the electron gyrofrequency. For homogeneous gyrotropic medium without fluctuating plasma parameters (2) takes the tensor form:
 (3)
(3)
Second rank permittivity tensor is expressed as:
 (4)
(4)
where  is the asymmetric tensor of the third rank. If the wave is propagating along the z axis and
is the asymmetric tensor of the third rank. If the wave is propagating along the z axis and  from (3) we obtain the set of homogeneous algebraic equations:
from (3) we obtain the set of homogeneous algebraic equations:
 (5)
(5)
components of  second rank tensor are:
second rank tensor are:

 ,
, 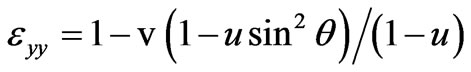 ,
, 
 ,
, 
 ,
, 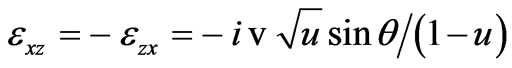 ,
, 
 ,
,
 is the angle between wave vector k and the external magnetic field
is the angle between wave vector k and the external magnetic field . If
. If  is non-dimensional parameter, we obtain the following dispersion relation:
is non-dimensional parameter, we obtain the following dispersion relation:
 , (6)
, (6)
the roots of which are:
 ,
,
 (7)
(7)
Two types of waves exist in homogeneous magnetized plasma under consideration. If 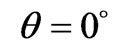 (longitudinal propagation of wave along the imposed magnetic field), taking into account
(longitudinal propagation of wave along the imposed magnetic field), taking into account ,
,  and
and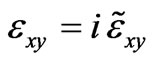 , (6) reduces to:
, (6) reduces to:  and has the roots:
and has the roots:
 and
and . Wave in hogeneous plasma propagates if
. Wave in hogeneous plasma propagates if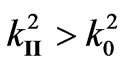 , i.e. the condition is fulfilled:
, i.e. the condition is fulfilled:

 . From these equations it follows that for the root
. From these equations it follows that for the root 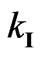 we have
we have 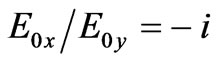 (corresponds to a right-handed circularly polarized wave) and for the second root
(corresponds to a right-handed circularly polarized wave) and for the second root  we have
we have  (corresponds to a left-handed circularly polarized wave). Since
(corresponds to a left-handed circularly polarized wave). Since 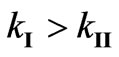 the rotation is clockwise. Faraday rotation angle is equal to
the rotation is clockwise. Faraday rotation angle is equal to  (z is the distance traveling by wave in the homogeneous plasma). We have estimated the angle using the following plasma parameters:
(z is the distance traveling by wave in the homogeneous plasma). We have estimated the angle using the following plasma parameters: ,
,  , which correspond to the mean values of the parameters in F region of the Earth’s ionosphere. The wavelength was chosen to be 100 m and the plasma parameters are equal to
, which correspond to the mean values of the parameters in F region of the Earth’s ionosphere. The wavelength was chosen to be 100 m and the plasma parameters are equal to ,
, Angle of Faraday rotation is
Angle of Faraday rotation is
 , which means that vector rotates anticlockwise. This conclusion is valid if the angle between the wave propagation and the external magnetic field is sharp.
, which means that vector rotates anticlockwise. This conclusion is valid if the angle between the wave propagation and the external magnetic field is sharp.
3. Statistical Characteristics of Electromagnetic Waves scattered by Turbulent Magnetized Plasma Slab
Let us calculate the second-order statistical moments of scattered radiation by turbulent magnetized plasma slab with electron density and magnetic field fluctuations. Each of the terms in (2) can be presented as the sum of the mean value and small fluctuating terms, which are random functions of the spatial coordinates: ,
,  ,
,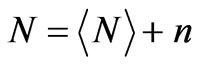 . The angular brackets indicate the statistical average. If the fluctuations are small, we can use perturbation method and fluctuating electric field satisfies the following differential equation [5]:
. The angular brackets indicate the statistical average. If the fluctuations are small, we can use perturbation method and fluctuating electric field satisfies the following differential equation [5]:
 , (8)
, (8)
where

is a current density,  ,
,
 ,
, 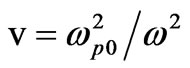 ,
,  ,
,
 ,
,  ,
,  are components of the second-rank tensor of collisionless magnetized plasma. At quasi-longitudinal propagation the determinant reduces to the biquadrate equation:
are components of the second-rank tensor of collisionless magnetized plasma. At quasi-longitudinal propagation the determinant reduces to the biquadrate equation:
 , (9)
, (9)
where the components of the dielectric permittivity are: ,
,  ,
,  ,
, 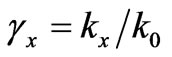 ,
,  ,
,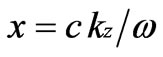 . Neglecting a small parameter
. Neglecting a small parameter , (9) can be rewritten as:
, (9) can be rewritten as:
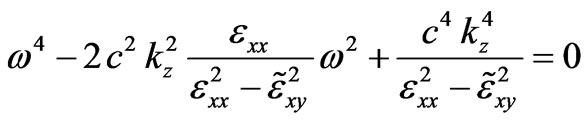 . (10)
. (10)
In the absence of an external magnetic field, from (10) we obtain the well-known dispersion equation:
 . If
. If  we have:
we have:
 , (11)
, (11)
where: ,
, . Expressions for the wave group velocity and dispersion are:
. Expressions for the wave group velocity and dispersion are:
 ,
,
 . (12)
. (12)
Using the perturbation method, the solutions of the stochastic differential Equation (8) satisfying the boundary conditions have the following form:
 , (13)
, (13)
 , (14)
, (14)
where  the transversal wave number,
the transversal wave number,
 ,
, 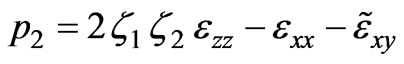 ,
,
 ,
,
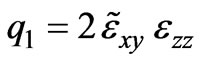 ,
,  ,
,
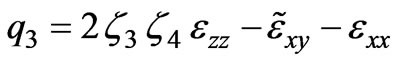 ,
, ,
,
 ,
,  ,
,
 ,
, 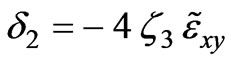 ,
,
 ,
,
 ,
, ,
,
 ,
, 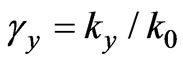 ,
,
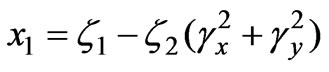 ,
, .
.
The mean field components
 are slowly varying function of z due to the attenuation of the mean field caused by transition of the mean field energy to the fluctuating one. We assume that the thickness of plasma slab is much smaller than the attenuation length and
are slowly varying function of z due to the attenuation of the mean field caused by transition of the mean field energy to the fluctuating one. We assume that the thickness of plasma slab is much smaller than the attenuation length and  is constant [5]. Square of the refractive index corresponding to the two normal waves propagating in the homogeneous magnetized plasma is determined with the well-known formula [6]:
is constant [5]. Square of the refractive index corresponding to the two normal waves propagating in the homogeneous magnetized plasma is determined with the well-known formula [6]:
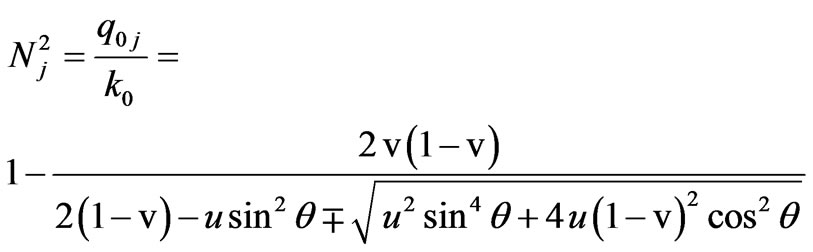 “
“ ” sign and index
” sign and index  correspond to the extra-ordinary wave, “+” sign and index
correspond to the extra-ordinary wave, “+” sign and index  correspond to the ordinary wave. If the scattered electromagnetic waves have quasi-longitudinal propagation
correspond to the ordinary wave. If the scattered electromagnetic waves have quasi-longitudinal propagation we have
we have . Second-order statis-ticcal moment of scattered electric field along the x axis and cross correlation function of scattered radiation in the
. Second-order statis-ticcal moment of scattered electric field along the x axis and cross correlation function of scattered radiation in the  plane has the following form:
plane has the following form:
 (15)
(15)
where  is the arbitrary two-dimensional wave number power spectrum of the electron density irregularities,
is the arbitrary two-dimensional wave number power spectrum of the electron density irregularities,  ,
, . This expression is valid for the near
. This expression is valid for the near  and far
and far  zones,
zones,  is the wavy parameter. Angular brackets indicate the statistical average.
is the wavy parameter. Angular brackets indicate the statistical average.
Spatial spectrum of the scattered field, which is of great practical importance, is the Fourier transformed correlation function of the scattered field. This statistical characteristic of the scattered radiation is equivalent to the ray intensity (brightness), which enters in the radiation transport equation. Phase fluctuations are determined by imaginary part of scattered electric field allowing to calculate structure function  and hence the angle-of-arrival of scattered radiation in the principle and perpendicular planes [1,4]:
and hence the angle-of-arrival of scattered radiation in the principle and perpendicular planes [1,4]:
 ,
,  (16)
(16)
In various measuring equipments (for example, in the systems measuring velocity of aircrafts) registering parameter is the frequency. In this case, frequency fluctuations caused by electromagnetic waves scattering on turbulence irregularities put the natural restrictions on the accuracy of measurements. Using the frozen-in turbulence hypothesis taking into account the velocity  of irregularities motion, the variance of the frequency fluctuation can be written in the following form:
of irregularities motion, the variance of the frequency fluctuation can be written in the following form:
 .
.
The index indicates a plane in which the broadening of the spectrum occurs. Introducing the frequency  and the carrier frequency
and the carrier frequency , the normalized intensity of frequency fluctuations will have the following form:
, the normalized intensity of frequency fluctuations will have the following form:
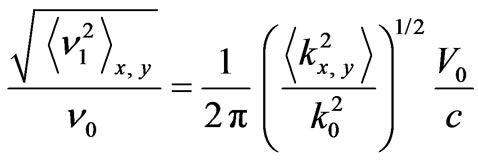 . (17)
. (17)
If  is the angle between the direction of drift velocity of irregularities and an observation line, correlation function of frequency can be written as:
is the angle between the direction of drift velocity of irregularities and an observation line, correlation function of frequency can be written as:
 . (18)
. (18)
Correlation function of frequency fluctuations is anisotropic due to the presence of the wind direction even at isotropic correlation function of phase fluctuations. From this expression it is possible to calculate and measure the horizontal drift velocity of plasma motion if other parameters are known.
Second order statistical moments allow to calculate the Stokes parameters [7]:
 ,
,


In general, the set of these parameters describe ellipticcally polarized wave. Degree of depolarization is the ratio of the unpolarized energy to the polarized energy:
 . (19)
. (19)
Note that depolarization effect and fluctuations of the angle-of-arrival are of the same order.
The Faraday Angle
It is well known that the radio waves propagating in the F region of the ionosphere at the frequencies satisfying the condition  can be registered on the Earth due to transformation of the ordinary wave into extraordinary one where relative concentration
can be registered on the Earth due to transformation of the ordinary wave into extraordinary one where relative concentration . The direction of the wave propagation should be close to the direction of the external magnetic field. According to the observations, direct estimation of a solid angle, under which radio waves arrive to the Earth, is of the order of 10–3 radian at the frequency of 0.5 MHz [8]. Linearly polarized wave in the Earth’s ionosphere generates the ordinary and extraordinary waves with slightly different phase velocities. The orthogonal linearly polarized waves determine the degree of Faraday rotation. Two-dimensional spectral electric fields for the ordinary and extraordinary electromagnetic waves scattered by plasma slab with random electron density pulsations propagating along the external magnetic field have the following form:
. The direction of the wave propagation should be close to the direction of the external magnetic field. According to the observations, direct estimation of a solid angle, under which radio waves arrive to the Earth, is of the order of 10–3 radian at the frequency of 0.5 MHz [8]. Linearly polarized wave in the Earth’s ionosphere generates the ordinary and extraordinary waves with slightly different phase velocities. The orthogonal linearly polarized waves determine the degree of Faraday rotation. Two-dimensional spectral electric fields for the ordinary and extraordinary electromagnetic waves scattered by plasma slab with random electron density pulsations propagating along the external magnetic field have the following form:
 (20)
(20)
where ,
, .
.
We assume that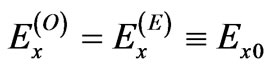 ,
, 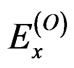 and
and 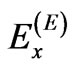 are the amplitudes of the linearly polarized ordinary and extraordinary waves,
are the amplitudes of the linearly polarized ordinary and extraordinary waves,  is the intensity of an incident wave;
is the intensity of an incident wave;  is connected with the finite width of this wave. Plane wave corresponds to the source remote at infinity, which is a good approximation at calculation of the statistical characteristics of fluctuating radio signals radiated from the geostationary satellites. Correlation function of scattered ordinary and extraordinary waves propagating along the external magnetic field for an arbitrary correlation function of electron density fluctuations could be written as:
is connected with the finite width of this wave. Plane wave corresponds to the source remote at infinity, which is a good approximation at calculation of the statistical characteristics of fluctuating radio signals radiated from the geostationary satellites. Correlation function of scattered ordinary and extraordinary waves propagating along the external magnetic field for an arbitrary correlation function of electron density fluctuations could be written as:
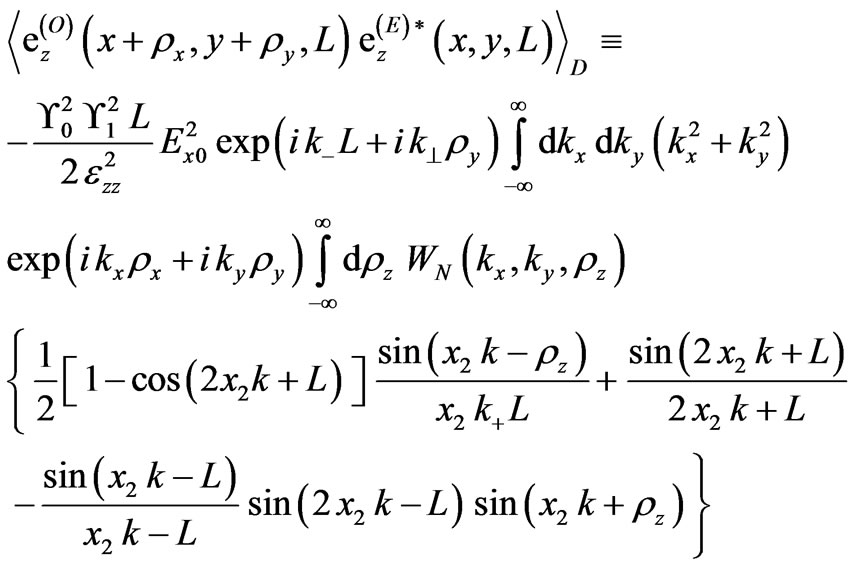 , (21)
, (21)
where . In isotropic case
. In isotropic case at
at , in the absence of an external magnetic field, the variance of the phase coincides with the well-known expression
, in the absence of an external magnetic field, the variance of the phase coincides with the well-known expression [8]. Rootmean-square deviation of the Faraday angle
[8]. Rootmean-square deviation of the Faraday angle  is determined by the expression:
is determined by the expression:
 . (22)
. (22)
Here  and
and 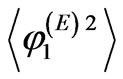 are the phase variances of the ordinary and extraordinary waves which can be obtained from the Equation (21).
are the phase variances of the ordinary and extraordinary waves which can be obtained from the Equation (21).
4. Numerical Results and Discussions
Experiments registering the phase difference of coherent signals radiating by the Earth satellite show that besides the regular phase difference in time, there are also irregular phase variations caused by the electron density irregularities. Information about the shape and dimensions of the ionospheric irregularities is obtained from the spatial-temporal measurements of scattered field on three spaced antennas. The measurements have shown a significant extension of the ionospheric irregularities along the geomagnetic field. Fluctuations may be caused by the irregularities of electron density of sizes  km and by the relative dispersion of the electron density
km and by the relative dispersion of the electron density
 .
.
Small-scale irregularities with Gaussian spectrum are responsible for polarization fluctuations at frequencies of 20 - 50 MHz. In case of forward scattering 
 , when the single scattering condition is fulfilled
, when the single scattering condition is fulfilled , the medium is characterized by the Gaussian irregularity spectrum. Therefore, in the analytical calculations we use anisotropic Gaussian correlation function of electron density fluctuation [10]:
, the medium is characterized by the Gaussian irregularity spectrum. Therefore, in the analytical calculations we use anisotropic Gaussian correlation function of electron density fluctuation [10]:
 , (23)
, (23)
where: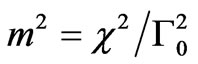 ,
, 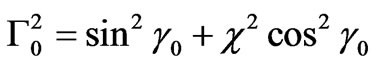 ,
,
 ,
,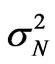 —variance of the electron density fluctuations. The average shape of electron density irregularities has the form of elongate ellipsoid of rotation. The ellipsoid is characterized with two parameters: the anisotropy factor
—variance of the electron density fluctuations. The average shape of electron density irregularities has the form of elongate ellipsoid of rotation. The ellipsoid is characterized with two parameters: the anisotropy factor  (ratio of longitudinal and transverse linear scales of plasma irregularities with respect to the external magnetic field) and the inclination angle
(ratio of longitudinal and transverse linear scales of plasma irregularities with respect to the external magnetic field) and the inclination angle  of prolate irregular-rities with respect to the magnetic field. Anisotropy of the shape of irregularities is connected with difference of the diffusion coefficients in the field align and field perpendicular directions.
of prolate irregular-rities with respect to the magnetic field. Anisotropy of the shape of irregularities is connected with difference of the diffusion coefficients in the field align and field perpendicular directions.
Statistical characteristics of scattered radiation are calculated at  using stationary phase method. Thickness of turbulent plasma slab is of the order of 200 km. Frequency of a linearly-polarized incident electromagnetic wave is 0.1 MHz
using stationary phase method. Thickness of turbulent plasma slab is of the order of 200 km. Frequency of a linearly-polarized incident electromagnetic wave is 0.1 MHz . The mean ionospheric height is taken to be 300 km with plasma parameters
. The mean ionospheric height is taken to be 300 km with plasma parameters  and
and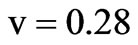 . If
. If ,
,
 from (17) we obtain
from (17) we obtain

which is in agreement with [8]. On the other hand, according to the frozen-in hypothesis, which disregards fluctuations of the drift velocity direction and evolution time (own lifetime) of inhomogeneities, at transversal motion of inhomogeneities, the width of the spectrum
 is of the order of
is of the order of  Hz (where
Hz (where
 is the transversal component of the drift velocity, L0—path length,
is the transversal component of the drift velocity, L0—path length, —wavelength).
—wavelength).
Spatial variations of the signal intensity accompanied by the angle-of-arrival fluctuations are measured by three receiving spaced antennas at the distances from a few hundred meters up to 1 - 2 km locating on the tops of a rectangular triangle. Numerical calculations show that the angles-of-arrivals approximately are the same in the principle and perpendicular planes; they decrease with increasing thickness of a turbulent plasma slab and the anisotropy factor. Particularly for the ionospheric F layer on the altitude 300 km, at the carrier frequency 0, 1 MHz , parameters of the ionospheric plasma slab:
, parameters of the ionospheric plasma slab: ,
, 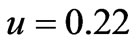 ,
,  km, if L = 100 km we obtain
km, if L = 100 km we obtain  at
at ;
;
 at
at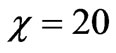 ; if
; if  km, we have
km, we have
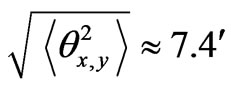 at
at , and
, and  at
at
 . At the frequency 6 MHz
. At the frequency 6 MHz , plasma slab parameters
, plasma slab parameters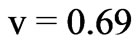 ,
,  ,
,  m;
m;
at 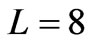 km, we obtain
km, we obtain , at
, at  km we have
km we have , which is agreement with the experimental data [8]. Calculating the Stokes parameters depolarization coefficient
, which is agreement with the experimental data [8]. Calculating the Stokes parameters depolarization coefficient  at
at  is equal to 0.2 at 0.1 MHz, and 0.7 at 40 MHz.
is equal to 0.2 at 0.1 MHz, and 0.7 at 40 MHz.
Figures 1 and 2 depict the dependence of the normalized second order statistical moments of scattered ordinary and extraordinary waves versus a distance between receiving antennas at the frequency of an incident wave 0.1 MHz and 40 MHz, respectively. Parameters of the ionospheric turbulent plasma slab are ,
, ;
; ,
,  (for 0.1 MHz) and
(for 0.1 MHz) and ,
,  (for 40 MHz),
(for 40 MHz),

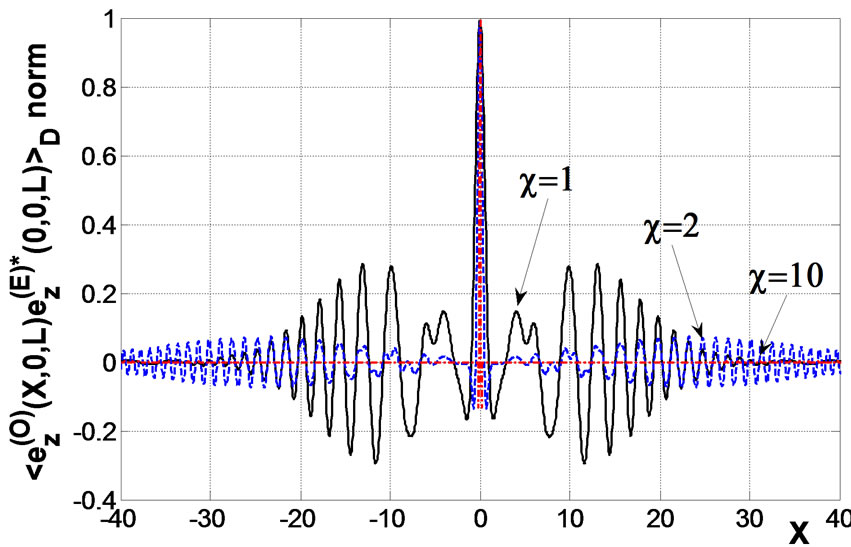
Figure 1. Normalized correlation function of scattered ordinary and extraordinary waves in the xoz and yoz planes, respectively, if the frequency of an incident wave is 0.1 MHz; at k0L = 120, L = 100 km,  km.
km.

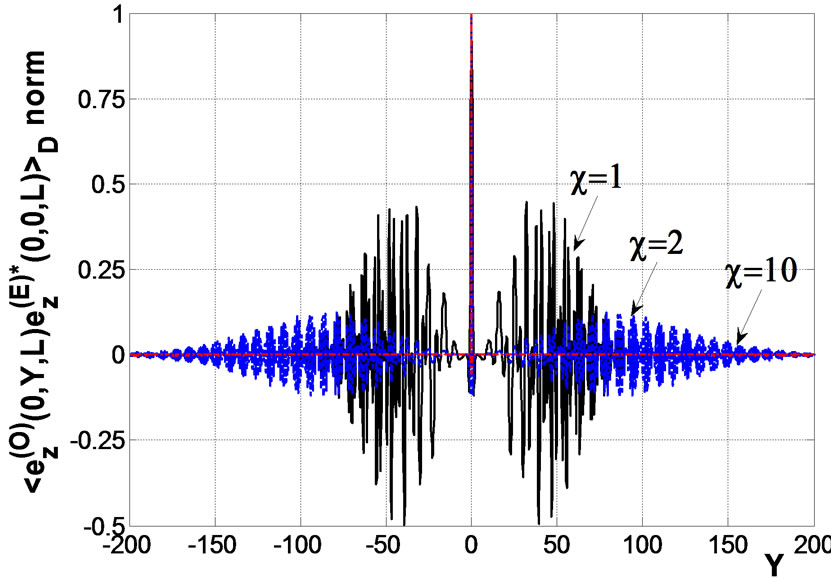
Figure 2. Normalized correlation function of scattered ordinary and extraordinary waves in the xoz and yoz planes, respectively, if the frequency of an incident wave is 40 MHz; at, k0L = 1.68 × 105, L = 200 km,  km.
km.
 . Thickness of the slab is equal 100 km (at 0.1 MHz) and 200 km (at 40 MHz), irregularities have field line direction
. Thickness of the slab is equal 100 km (at 0.1 MHz) and 200 km (at 40 MHz), irregularities have field line direction ;
; 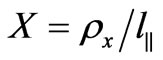 and
and  are normalized distances between the observation points.
are normalized distances between the observation points.
Analysis show that correlation between ordinary and extraordinary waves decreases in proportion to the anisotropic factor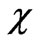 . Fluctuations of the Faraday angle
. Fluctuations of the Faraday angle  in the ionosphere are caused by scattering of an incident linearly-polarized wave on random inhomogeneities of electron density fluctuations. Pronounced fluctuations
in the ionosphere are caused by scattering of an incident linearly-polarized wave on random inhomogeneities of electron density fluctuations. Pronounced fluctuations  of polarization twist were registered at receiving signals from radio beacons of low-altitude satellites at the frequencies of 20 - 50 MHz. At the frequencies exceeding electron gyrofrequency the main effect related with the magnetic field is the Faraday rotation of linearly polarized wave. The rotation is caused by a continuous variation of the phase difference of two circularly polarized waves having opposite rotation directions [6-8].
of polarization twist were registered at receiving signals from radio beacons of low-altitude satellites at the frequencies of 20 - 50 MHz. At the frequencies exceeding electron gyrofrequency the main effect related with the magnetic field is the Faraday rotation of linearly polarized wave. The rotation is caused by a continuous variation of the phase difference of two circularly polarized waves having opposite rotation directions [6-8].
Two receiving antennas are located in orthogonal planes. Faraday angle increases in proportion of the frequency of an incident wave in the interval of 50˚ - 400˚, while for metric electromagnetic waves it was equal to . Isolines of the normalized root-mean-square deviation of the Faraday angle nonlinearly depend on the angle of inclination of prolate irregularities and increase in proportion to the anisotropy factor. Isolines of the variance of the Faraday angle
. Isolines of the normalized root-mean-square deviation of the Faraday angle nonlinearly depend on the angle of inclination of prolate irregularities and increase in proportion to the anisotropy factor. Isolines of the variance of the Faraday angle  normalized on the variance of electron density fluctuations
normalized on the variance of electron density fluctuations  are shown in Figure 3.
are shown in Figure 3.
5. Conclusions
Second order statistical moments of the electric field scattered by a magnetized inhomogeneous plasma slab perpendicular to the external magnetic field are derived using the perturbation method. The obtained results are valid for near and far zones with respect to plasma slab boundaries. Analytical and numerical studies are carried out for the anisotropic Gaussian correlation function of electron density fluctuations taking into account the anisotropy factor and the angle of inclination of prolate irregularities with respect to the external magnetic field. Analytical expression of the mutual correlation function of the scattered ordinary and extraordinary waves having quasi-longitudinal propagation along the external magnetic field is derived for arbitrary second-order moments of electron density fluctuations. It is shown that the correlation between these waves fast decreases with in proportion of the anisotropy factor. The normalized variance of the Faraday angle nonlinearly depends on the angle of inclination of prolate irregularities. The isolines are constructed when the receiving antennas are located in the perpendicular planes.