Evaluation of Excitation Functions of Reactions Used in Production of Some Medical Radioisotopes

Idris Ahmad^*, Yahya Ibrahim Yola, Fatima Salman Koki

Department of Physics, Bayero University Kano, Kano, Nigeria.

DOI: 10.4236/ijmpcero.2017.63026                

Abstract

In this work, reaction cross-sections were calculated and Excitation Functions were evaluated for productions of ²⁰⁸Bi, ^212,211,210At, ^211,210Po isotopes using EXIFON code in the energy range from 0 MeV to 30 MeV. The code is based on an analytical model for statistical multistep direct and multistep compound reactions (SMD/SMC model). This work also investigates the shell structure effect on the reaction cross-section, the results obtained show that the cross-sections of (a, na) reaction for both with shell correction and without shell correction are zeros at energies range considered, this shows that the energy of the incident particle is below the threshold of this reaction due to the present of coulomb repulsive force between the projectile and target nucleus.

Keywords

Nuclear Reaction, Cross-Section, Excitation Function, Radioisotope, Nuclear Model

1. Introduction

Studies of excitation functions of particle-induced reactions are of considerable significance for testing nuclear models as well as for practical applications, especially in cyclotron production of radioisotopes [1] . Nuclear reaction in the intermediate-energy region is a matter of interest in some fields of technology and science such as reactor technology, radiation therapy in nuclear medicine, medical radionuclide production, diagnostic and therapeutic studies, Accelerator Driven Systems , fusion and fission reactor. The artificially produced radioactive isotopes are important for many different applications [2] [3] [4] [5] . Radioactive isotopes play an important role in the field of medical science in terms of beneficial applications in both diagnosis and therapy purposes [6] . In radioisotope production programmers, nuclear reactions data are mainly needed for optimization of production routes [7] [8] [9] . The cross section data for different nuclide was intensively investigated and up to now, the nuclear databases are accessible online [10] - [22] .

A nuclear reaction is a process that occurs when a nuclear particle (nucleon or nucleus) gets into close contact with another [23] . In the general case, an arbitrary number of particles may emerge. The probability of the reaction processes as a function of the energy of the incident particle, in the energy and the direction of the outgoing particles is usually interested in the whole set of reactions.

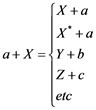(1.1)

The first two reactions (1.1) are distinguished by the fact that the projectile re-emerges after the reaction. The first of these represents elastic scattering. The second reaction represents inelastic scattering.

To calculate the reaction cross section, it is necessary to compute the number of particles that disappear from the elastic channel, what is measured by the flux of the current of probability vector through a spherical surface of large radius centered at the target [24]

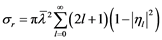(1.2)

A radial wave function inside the nucleus should connect to the external function with a continuous function and its derivative at.

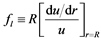(1.3)

The function must have identical values if calculated with the internal or the external function and this condition creates a relationship between and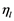. Hence, the knowledge of 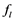leads to the knowledge of the cross sections [24] .

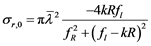(1.4)

We have an equation that is useful when we study the presence of resonances in the excitation function (cross section as a function of the energy).

Statistical multistep model

Statistical multistep models are very successful in describing nuclear reactions at energies up to about 100 MeV [25] . These models enable the description of direct, pre-equilibrium, and equilibrium processes in a consistent way for a wide mass number range and various reaction channels, e.g. neutrons, protons, alpha-particles, and gamma-particles.

In the statistical multistep model, the total emission spectrum of the process is divided into three main parts [14] [26] ,

(1.5)

The first term on the right hand side of Equation (1.5) represents the statistical multistep direct (SMD) part which contains from single-step up to five-step contributions. The second term represents the statistical multistep compound (SMC) emission which is based on a master equation. Both terms together (SMD + SMC) represents the first-chance emission process [27] [28] . The last term of Equation (1.5) represents the multiple particle emission (MPE) reaction which includes the second-chance, third-chance emissions, etc. These terms are summarized below:

(1.6)

The following relations between the optical model (OM) reaction cross section and the energy-integrated partial cross sections should be satisfied (at each incident energy)

(1.7)

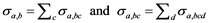(1.8)

With

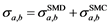the total first-chance emission. In this context, activation cross sections are given by

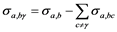(1.9)

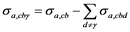(1.10)

where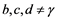

For example, the (n,p)-activation cross sections have the form

(1.11)

The SMD cross section is a sum over s-step direct processes given by: [29]

(1.12)

The SMD cross section has the form

(1.13)

where satisfies the time-integrated master equation

(1.14)

and

(1.15)

The multiple particle emission is expressed as:

(1.16)

To keep the model tractable, a simple two-body interaction is assumed: [27]

(1.17)

taken from nuclear structure considerations.

The factor contains the wave function at the nuclear radius

The single-particle state density of particles with mass is given by

(1.18)

Where is equal to the nuclear volume [26] .

The single-particle state density of bound particles (at Fermi energy) is then defined by

(1.19)

Where the factor 4 considers the spin and isospin degeneracy

2. Procedure

EXIFON code was used which is computer program package for computational nuclear Data physics which is based on an analytical model for statistical multistep direct and multistep compound reactions (SMD/SMC model). It predicts emission spectra, angular distributions, and activation cross sections for neutrons, protons, alpha particles, and photons. Multiple particle emissions are considered for up to three decays of the compound system. EXIFON is a fast, easy-to-handle code which predicts cross sections from one global parameter set. The only adjustable quantity is the pairing shift. The INPEXI code creates input files for EXIFON2.0 from mass and shell-correction tables. The MAKE6 code transforms EXIFON output into an ENDF-6 format file [26] . It is tested and recommended code by international atomic energy agency (IAEA).

The model is based on random matrix physics with the use of the Green’s function formalism [29] [30] . All calculations are performed without any free parameters. Results were presented for bombarding energies below 30 MeV [31] [32] .

2.1. Cross section Calculations

The program was run and the input and output directory was defined, and then the target nucleus is specified. The neutron was chooses as incident particle followed by selecting the target nucleus and excitation function in the general option section for this calculation.

The number of incident energy was specified followed by the first incident energy, and then the incident energy step is also specified. The cross section correspond to each particular energy was obtained.

2.2. Shell Structure Effects

The shell structure effects are considered in SMC processes. Under such a situation, the single-particle state density g, in Equation (1.19) is multiplied by the factors

(2.1)

With and as the shell correction energy taken from tables [33] where the quantity which denotes the excitation energy of the composite or residual systems respectively.

The calculations in this study were performed with and without shell corrections. The procedures in 2.1 and 2.2 were repeated several times and the results of cross sections were obtained.

3. Results and Discursions

The cross section obtained was tabulated in hot-pot Figures 1-3 and the excita-

Figure 1. Cross sections at different incident energies for (a, a), (a, na), (a, ag), (a, an) reactions.

Figure 2. Excitation function ²⁰⁸Bi(a,a) ²⁰⁸Bi reaction.

Figure 3. Excitation function ²⁰⁸Bi(a,ag) ²⁰⁸Bi reaction.

tion function was showed in Figures 1-10. The calculations in which the shell correction was taken into consideration are denoted by “With shell correction” on the graph’s legend, while those without the shell correction effects are denoted by “Without shell correction”.

In hot-pot Figure 1, One can observe that the cross sections for ²⁰⁸Bi(a, na)²⁰⁷Bi and ²⁰⁸Bi(a, an)²⁰⁷Bi reactions are zeros. This shows that these two reactions would not occur at the incident energy of (0 - 30) MeV.

Figure 2 and Figure 3 are graphs of cross section against incident energy of the alpha particle,

The two reactions are distinguished by the fact that the projectile re-emerges after the reaction. The first of these represents elastic scattering. The second reaction represents inelastic scattering in Equation (2.3).

Figure 4. Cross sections at different incident energies for (a, g), (a, ng), (a, pg), (a, 2ng) reactions.

Figure 5. Excitation function ²⁰⁸Bi(a, g)²¹²At reaction.

Figure 6. Excitation function ²⁰⁸Bi(a, ng)²¹¹At reaction.

Figure 7. Excitation function ²⁰⁸Bi(a, pg)²¹¹Po reaction.

Figure 8. Excitation function ²⁰⁸Bi(a, 2ng)²¹⁰At reaction.

Figure 9. Cross sections at different incident energies for (a, n), (a, 2n), (a ,pn), (a, 3n) reactions.

Figure 10. Excitation function ²⁰⁸Bi(a, n)²¹¹At reaction.

Figures 5-8 are graphs of cross section against incident energy of the alpha particle, ²⁰⁸Bi(a, g)²¹²At is a compound nucleus formation of Astatine(212) followed by gamma emission. ²⁰⁸Bi(a, ng)²¹¹At is a knock out reaction for the nucleus formation of Astatine (211) followed by gamma emission. ²⁰⁸Bi(a, pg)²¹¹Po is also a knock out reaction for the nucleus formation of Polonium (211) followed by gamma emission. ²⁰⁸Bi(a, 2ng)²¹⁰At is also a knock out reaction for the nucleus formation of Astatine(210) followed by gamma emission. All the results shows that shell structure correction does not much changes at the range of energies from (0 - 30) MeV.

Figures 10-13 are graphs of cross section against incident energy of the alpha particle, ²⁰⁸Bi(a, n)²¹¹At is a knock out reaction for the nucleus formation of Astatine (211). ²⁰⁸Bi(a ,2n) ²¹⁰At is also a knock out reaction for the nucleus formation of Astatine (210) ²⁰⁸Bi(a, pn)²¹⁰Po is also a knock out reaction for the nucleus formation of Polonium (210). ²⁰⁸Bi(a, 3n)²¹¹At is a knock out reaction for the nucleus formation of Astatine (209) All the results shows that shell structure correction does not much changes at the range of energies from (0 - 30) MeV except for ²⁰⁸Bi(a, 3n) ²¹²At reaction although the cross section value is very small.

4. Conclusion

Nuclear reaction in the intermediate-energy region is a matter of interest in some fields of technology and science such as reactor technology, radiation therapy in nuclear medicine, medical radionuclide production, diagnostic and therapeutic studies, Accelerator Driven Systems (ADS), fusion and fission reactor. Radioactive isotopes play an important role in the field of medical

Figure 11. Excitation function ²⁰⁸Bi(a, 2n)²¹⁰At reaction.

Figure 12. Excitation function ²⁰⁸Bi(a, pn)²¹⁰Po reaction.

Figure 13. Excitation function ²⁰⁸Bi(a, 3n) ²¹²At reaction.

science in terms of beneficial applications in both diagnosis and therapy purposes. The reaction cross-sections were calculated and Excitation Functions were evaluated for productions of ²⁰⁸Bi, ^212,211,210At, ^211,210Po isotopes in the energy range from 0 MeV to 30 MeV. We also investigate the shell structure effect on the reaction cross-section, the results obtained show that the cross-section of (a, na) reaction for both with shell correction and without shell correction are zeros at energies range considered, this shows that the energy of the incident particle is below the threshold of this reaction due to the present of coulomb repulsive force between the projectile and target nucleus. The application in precise evaluation of the Excitation Functions as well as the production of isotopes is necessary to embrace the current and future needs for medical radionuclide.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Al-Abyad, M., Comsan, M.N.H. and Qaim, S.M. (2009) Excitation Functions of Proton-Induced Reactions on Nature Fe and Enriched 57Fe with Particular Reference to the Production of 57Co. Applied Radiation and Isotopes, 67, 122-128.
[2]	Srivastava, S.C. (1996) Therapeutic Radionuclides: Making the Right Choice. Kluwer Academic Publishers, Dordrecht, 63-79.
[3]	Srivastava, S. and Mausner, L.F. (1971) Concepts of Nuclear Physics. McGraw-Hill Book Co., New York, Vol 25, 1971.
[4]	Sadeghi, M. and Enferadi, M. (2011) Nuclear Model Calculations on the Production of 119. Sb via Various Nuclear Reactions. Annals of Nuclear Energy, 38, 825-834.
[5]	Al-saleh, F.S., Al Mugren, K.S. and Azzam, A. (2007) Zn (p, x) Reactions at Low Energies. Applied Radiation and Isotopes, 65, 1101-1107. https://doi.org/10.1016/j.apradiso.2007.05.004
[6]	Kettern, K., Coenen, H.H. and Qaim, S.M.Ã. (2009) Quantification of Radiation Dose from Short-Lived Positron Emitters Formed in Human Tissue Under Proton Therapy Conditions. Radiation Physics and Chemistry, 78, 380-385. https://doi.org/10.1016/j.radphyschem.2008.12.006
[7]	Abusaleem, K. (2014) Nuclear Data Sheets for A = 228. Nuclear Data Sheets, 116, 163-262.
[8]	Akovali, Y.A. (2004) Nuclear Data Sheets for A = 243. Nuclear Data Sheets, 103, 515-564.
[9]	Nichols, A.L. (2002) Nuclear Data Requirements for Decay Heat Calculations. Lectures Given at the Workshop on Nuclear Reaction Data and Nuclear Reactors: Physics, Design and Safety. Trieste, 25 February - 28 March 2002, 67-195.
[10]	Basu, S.K. and Sonzogni, A.A. (2013) Nuclear Data Sheets for A = 95. Nuclear Data Sheets, 114, 435-660. https://doi.org/10.1016/j.nds.2013.04.001
[11]	Filatenkov, A.A and Chuvaev, S.V. (2000) Measurement of Cross Section for Reaction 241Am(n, 2n) and 241Am(n, 3n). Physics of Atomic Nuclei, 63, 1504-1510. https://doi.org/10.1134/1.1312883
[12]	Klopries, B.R.M., Sudärs, S.R.D.S.S. and Qaim, S.M. (1997) Excitation Functions of Some Neutron Threshold Reactions on 89Y. Radiochimica Acta, 9, 3-9.
[13]	Probst, H.J. and Qaim, S.M. (1976) Excitation Functions of High-Energy α-Particle Induced Nuclear Reactions on Aluminium and Magnesium: Production of 28 Mg. International Journal of Applied Radiation & Isotopes, 27, 431-441. https://doi.org/10.1016/0020-708X(76)90062-4
[14]	Nesaraja, B.C., Linse, K., Spellerberg, S., Sudar, S., Suhaimi, A. and Qaim, S.M. (1999) Excitation Functions of Neutron Induced Reactions on Some Isotopes of Zinc, Gallium and Germanium in the Energy Range of 6.2 to 12.4 MeV. Radio-chimica Acta, 9, 1-9. https://doi.org/10.1524/ract.1999.86.12.1
[15]	Uddin, M.S., Scholten, B., Hermanne, A., Sudár, S., Coenen, H.H. and Qaim, S.M. (2010) Radiochemical Determination of Cross Sections of α-Particle Induced Reactions on 192Os for the Production of the Therapeutic Radionuclide 193MPt. Applied Radiation and Isotopes, 68, 2001-2006. https://doi.org/10.1016/j.apradiso.2010.05.002
[16]	Hussain, M., Sudar, S., Aslam, M.N., Shah, H.A., Ahmad, R., Malik, A.A. and Qaim, S.M. (2009) A Comprehensive Evaluation of Charged-Particle Data for Production of the Therapeutic Radionuclide 103 Pd. Applied Radiation and Isotopes, 67, 1842-1854. https://doi.org/10.1016/j.apradiso.2009.06.010
[17]	Kastleiner, S., Qaim, S.M., Nortier, F.M., Blessing, G., Van, T.N.W. and Coenen, H.H. (2002) Excitation Functions of 85Rb (P, Xn) (85M, G, 83, 82, 81) Sr Reactions up to 100 MeV: Integral Tests of Cross Section Data, Comparison of Production Routes of 83 Sr and Thick Target Yield of 82 Sr. Applied Radiation and Isotopes, 56, 685-695. https://doi.org/10.1016/S0969-8043(01)00267-6
[18]	Qaim S.M. and Weinreich, R. (1977) Excitation Functions for the Formation of Neutron Deficient Isotopes of Bromine and Krypton via High-Energy Deuteron Induced Reactions on Bromine: Production of 77 Br, 76 Br and 79 Kr. International Journal of Applied Radiation & Isotopes, 28, 947-953. https://doi.org/10.1016/0020-708X(77)90059-X
[19]	Qaim, S.M., Sudár, S., Scholten, B., Koning, A.J. and Coenen, H.H. (2014) Evaluation of Excitation Functions of 100Mo (P, D + Pn) 99Mo and 100Mo (P, 2N) 99MTc Reactions: Estimation of Long-Lived Tc-Impurity and Its Implication on the Specific Activity of Cyclotron-Produced 99mTc. Applied Radiation and Isotopes, 85, 101-113. https://doi.org/10.1016/j.apradiso.2013.10.004
[20]	Uddin, B.M.S., Baba, M., Hagiwara, M., Latif, S.K.A. and Qaim, S.M. (2008) Excitation Functions for the Formation of Some Short-Lived Products in Proton-Induced Reactions on Silver. Radiochimica Acta, 72, 67-72.
[21]	Hilgers, K., Coenen, H.H. and Qaim, S.M. (2008) Production of the Therapeutic Radionuclides 193MPt and 195MPt with High Specific Activity via α-Particle-Induced Reactions on 192Os. Applied Radiation and Isotopes, 66, 545-551. https://doi.org/10.1016/j.apradiso.2007.10.009
[22]	Menapace, E., Birattari, C., Bonardi, M.L., Groppi, F., Morzenti, S. and Zona, C. (2005) Comparison between Theoretical Calculation and Experimental Results of Excitation Functions for Production of Relevant Biomedical Radionuclides. Proceedings of American Institute of Physics International Conference on Nuclear Data for Science and Technology, Santa Fe, NM, USA, 26 september - 1 October , 2005, 1638. https://doi.org/10.1063/1.1945321
[23]	Al-Saleh, A.A.F.S. and Al-Mugren, K.S. (2007) Exitation Functions of (P, X) Reactions on Natural Nickle between Proton Energies of 2.7 and 27.5 MeV. Applied Radiation and Isotopes, 65, 104-113. https://doi.org/10.1016/j.apradiso.2006.06.013
[24]	Bertulani, C.A. (2009) Nuclear Reactions. Physics, 1, 1-26. https://doi.org/10.1002/3527600434.eap277.pub2
[25]	Polster, D. and Kalka, H. (1991) Short Note Fission within a Statistical Multistep Model. Zeitschrift für Physik a Hadrons & Nuclei, 424, 423-424. https://doi.org/10.1007/BF01560648
[26]	Ebiwonjumi, Y.E.C.B.F. (2014) Determination of Nuclear Reaction Cross-Sections for Neutron-Induced Reactions in Some Odd—A Nuclides. Advances in Physics Theories & Applications, 32, 55-69.
[27]	Kalka, H. (1992) Hadrons and Nuclei Statistical Multistep Reactions from 1 to 100 MeV. Zeitschrift für Physik a Hadrons & Nuclei, 299, 289-299. https://doi.org/10.1007/BF01283537
[28]	Qaim, S.M. (1986) Recent Developments in the Production of 18F, 75,76,77Br and I-123. International Journal of Radiation Applications and Instrumentation. Part A. Applied Radiation and Isotopes, 37, 803-810.
[29]	Muhammed, K., Onimisi, M.Y. and Jonah, S.A. (2011) Investigation of the Shell Effect on Neutron Induced Cross Section of Actinides. Journal of Nuclear & Particle Physics, 1, 6-9. https://doi.org/10.5923/j.jnpp.20110101.02
[30]	Watanabe, Y., Fukahori, T., Kosako, K., Shigyo, N., Murata, T., Yamano, N., Hino, T., Maki, K., Nakashima, H., Odano, N. and Chiba, S. (2005) Nuclear Data Evaluations for JENDL High-Energy File. International Conference on Nuclear Data for Science and Technology, 769, 326-331.
[31]	Ford, H. (2012) Radiation Safety Information Computational Center Changes to the RSICC Code and Data Collection. Lawrence Livermore National Laboratory, Livermore, 1-13.
[32]	White, J.E., Manneschmidt, J.B., Finch, S.Y. and Dickens, J.K. (1997) Abstracts of Computer Programs and Data Libraries Pertaining to Photon Production Data. Office of Scientific & Technical Information Technical Reports, 32, 101-103.
[33]	Yamoah, S. and Asamoah, M. (2013) Calculations of Excitation Functions of (N, P), (N, A) and (N, 2N) Reaction Cross-Sections for Stable Isotopes of from Reaction Threshold to 20 MeV. Optics Communications, 3, 100-107.