A Direct Algorithm for the Vertical Generalized Complementarity Problem Associated with P-Matrices

Aniekan Ebiefung¹, George Habetler², Michael Kostreva³, Bohdan Szanc⁴

¹Department of Mathematics, University of Tennessee, Chattanooga, USA.
²Department of Mathematical Sciences Rensselaer Polytechnic Institute, Troy, USA.
³Department of Mathematical Sciences Clemson University, Clemson, USA.
⁴Department of Mathematics Maryville University, St. Louis, USA.

DOI: 10.4236/ojop.2017.63008                

Abstract

We present a direct algorithm for solving the vertical generalized linear complementarity problem, first considered by Cottle and Dantzig, when the associated matrix is a vertical block P-matrix. The algorithm converges to a unique solution in a finite number of steps, without an assumption of nondegeneracy on the given problem. The algorithm is simple, efficient, and easy to implement.

Keywords

Complementarity Problems, P-Matrix, Direct Algorithms, Linear Programming, Bi-Matrix Game

1. Introduction

The linear complementarity problem for any 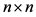matrix M is defined as follows:

For any given, find such that

(1)

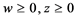
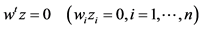
The study of linear complementarity problems (LCPs) began in the 1960s. Linear programming, quadratic programming, bi-matrix games, as well as cer- tain problems in economics and engineering, can be represented as LCPs.

Murty [1] presented an algorithm that finds a unique solution to (1) in a finite number of steps, if the matrix M associated with the problem is an 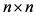P- matrix.

The vertical generalized linear complementarity problem for an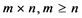, vertical block matrix N of type 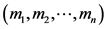is:

For any given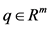, find 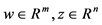such that

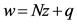
(2)

We will denote this problem by VGLCP(q, N). For a horizontal generalization of the LCP, see the paper by Chakraborty and Ebiefung [2] .

In 1970 Cottle and Dantzig published the first paper to describe the VGLCP [3] . They showed that if N is a strictly positive (or copositive plus) vertical block matrix or a P-matrix, the VGLCP(q, N) has a solution, and also introduced a technique for solving the VGLCP(q, N), when N is a copositive plus vertical block matrix. Their technique could be considered as an extension of Lemke’s algorithm for the LCP (with covering vector e) [4] .

The fact that the VGLCP(q, N) has a unique solution when N is a vertical block P-matrix was established by Habetler and Szanc [5] , while existence of solutions in terms of representative submatrices was developed by Ebiefung [6] . The set of Q-matrices for the VGLCP(q, N) was characterized by Ebiefung [7] , and by Ebiefung and Kostreva [8] . In [8] , an algorithm for solving the GLCP for any vector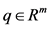, irrespective of the matrix class, is also provided. As expected, the method they provided is complicated and expensive to implement. For this reason, specialized algorithms are needed when properties of the associated matrices can be exploited to have simpler algorithms. One of these specialized algorithms for the VGLCP is given in Ebiefung, Kostreva, and Ramanujam [9] , where the associated matrix is a vertical block Z-matrix.

Applications of Vertical Complementarity Problems are becoming more prevalent. One engineering application is that of Mixed Lubrication which was discussed in the paper of Oh [10] . Calculations were made on a journal bearing with elastic support to illustrate the method of solution over a wide range of conditions. Regions of solid-to-solid contact, hydrodynamic lubrication, and cavitation were observed. The solutions were obtained using a version of the direct algorithm presented here. No proof of convergence was given, and the solution of the generalized complementarity problem is contained in one short paragraph.

In the area of economics, the VGLCP has been applied to the generalization of Leontief’s production model and the choice of technology by Ebiefung and Kostreva [11] ; and to the determination of equilibrium points in multi-unit manufacturing systems, Ebiefung and Kostreva [12] . Other economic applica- tions can be found in Ebiefung, Kostreva, and Majumdar [13] , Ebiefung and Isaac [14] , Ebiefung [15] , and in the references at the end of this paper.

In this paper, we modify Murty’s direct algorithm to solve the LCP when the associated matrix N is a vertical block P-matrix of type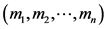. We will show that the new algorithm finds a non-negative solution to problem VGLCP(q, N) in a finite number of steps, where 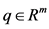and N is a vertical block P-matrix of type.

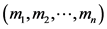The theory needed to prove finite convergence of the direct algorithm is given in detail in [5] , and will be covered briefly here. Finite convergence of the algorithm is essential. As we pointed out before, Cottle and Dantzig’s algorithm is an extension of Lemke’s algorithm which could cycle (or loop) as pointed out by Kostreva [16] . In fact, the example given by Kostreva can be easily modified to show that their algorithm can cycle. Such behavior in a computation would cause a failure in any implementation. Thus, another approach is motivated. It should be noted that the computer routine of Ravindran [17] does cycle when applied to the example of a P-matrix given in [16] .

The rest of the paper is organized as follows. In Section 2, we give notation and definitions that are needed for the rest of the paper. Section 3 is devoted to the description of the new algorithm and proof of convergence. We summarize our results in Section 4.

2. Notation and Definitions

The following notation and definitions are needed for the development of the algorithm.

Definition 1. Let N be an rectangular matrix with. We call N a vertical block matrix of type if N can be partioned row-wise as

where the jth block, , is of dimension and. The

vectors and are also partitioned to conform to the entries in the block, of:

where and are column vectors.

Associated with problem (2) is the related problem: given, find such that

(3)

Definition 2. By a horizontal matrix A of type, we shall mean a matrix

where the jth block of, is a matrix and.

The linear system in (3) can be re-written in the form

where I is the identity matrix. We shall represent I as a horizontal block matrix by

where is the jth block of columns associated with the variable. Thus is an matrix and. The column vector is associated with the variable and the column vector is associated with the variable.

Definition 3. Let N be an, vertical block matrix of type. Let I be an horizontal block identity matrix of type. Define B as the horizontal block matrix of type given by

such that the ith column of the jth block of columns, , is either or, and if for any, we have

then for that specific j

for all. We call B a basic matrix. The vertical block matrix N of type is said to be nondegenerate if and only if for each such basic matrix B, taking all possible combinations, B is nonsingular.

Definition 4. The vector in system (2) is nondegenerate with respect to N if for each at most n of the variables are zero.

Definition 5. For each j, , the variables

constitute the jth ordered related -tuple. The set of columns will be known as the jth ordered related set of column vectors in system (2).

Definition 6. A related basic matrix associated with system (3) is the horizontal block matrix B of type defined in Definition 3. The set of variables corresponding to the jth block of columns of, are called the jth related set of basic variables. The variables that are excluded from the jth set

of basic variables are called nonbasic. There are possible related basic matrices associated with system (3) and we shall denote these basic related matrices by

will always denote the horizontal block identity matrix. This is equivalent to requiring that be the nonbasic variable for

We now consider the solutions corresponding to the related

basic matrices associated with the system (3).

If a solution exists to the following system

we will call the solution a basic related point, and denote it by. The vector is subdivided in accordance with, i.e. and.

Definition 7. A basic related point is called degenerate if at least one of its components is zero.

Consider the related problem (3). To satisfy the related condition,

at least one component of the jth ordered related -tuple, , must be assigned the value zero.

We call this component the related nonbasic variable associated with, and we will denote it by. If each is an ordered related vector, i.e. satisfies the related condition for each, we must have for each and some

or

We denote the related nonbasic vector associated with by

The components of that are left if we eliminate are called the related basic variable of and denoted by. The jth ordered block of related columns associated with is denoted by:

For each and each, we denote the columns associated with by. If we eliminate the columns of from the columns of, we are left with the column that is considered nonbasic. We will denote this column by, and this column will be associated with the nonbasic variable.

Using this notation, we can rewrite Equations (2) as follows:

For any given, find such that

(4)

If is nonsingular, we can find an explicit expression for and a solution to Equation (4) would have to satisfy

3. The Algorithm

The algorithm that we prepose is described as follows:

Step 1: If, then is the related solution to Equations (2). Terminate.

Step 2: Suppose. Start the scheme by picking w as the initial related basic vector,. Then. Go to Step 3.

Step 3: All the matrices obtained during the scheme will be basic related

matrices,. In a general stage of the scheme, suppose

that is the present basic related matrix. If, we are done. The basic related vector represents the basic related variables and represents the nonbasic related variables of the solution of Equations (2). Terminate.

Step 4: If or, find

Interchange the related basic variable represented by and the related nonbasic variable represented by. This is equivalent to interchanging the columns and. After rearranging the columns of the result matrix, if necessary, to conform with Definition 3, denote the resulting related basic matrix by, that is, increase by 1. Continue the scheme as above until there exits a related basic matrix, such that

Definition 8. If N is a vertical block matrix of type, then H is defined to be the submatrix of type if H is the matrix that results from eliminating the nth block and the nth column of N.

Definition 9. Let

The generalized vertical linear complementarity problem for the leading submatrix H is:

Given, find such that

(5)

Problem (5) is called the leading subproblem of Equations (2).

The related basic matrices associated with (5) are the matrices given by Definition 2. The associated related basic and nonbasic vectors are denoted by and, respectively.

Lemma 1 Suppose is a solution of Equations (2) and that. Let

Then is a solution of problem (5).

Proof: Since, we have that

The positivity and satisfied related condition for follows from the definition of.

Lemma 2 If is a solution to problem (5), let. Suppose

Then is a solution to Equations (2), where.

Lemma 3 If N is a vertical block matrix of type, then is vertical block P-matrix of type and the leading subproblem has a unique solution.

Proof: Any representative submatrix of H is a leading submatrix of a representative submatrix of N. Every leading submatrix of N is an P-matrix.

Therefore, H is a vertical block P-matrix of type and therefore, a unique solution exists for Equations (5).

Lemma 4 Let be a vertical block P-matrix of type and let be the unique solution of Equation (2). Suppose. For some

, let

be the related nonbasic and basic vectors associated with the unique solution to Equations (5). Then

are the related basic and nonbasic vectors associated with the solution.

Proof: Let be the unique solution to Equations (5), then and represent the related nonbasic and basic vectors, respectively of.

Since is the unique solution to Equations (2) and, we have and Lemma 2 implies that

Since the first blocks of and are the same and the first components of and are the same, we must have

Theorem 5 Suppose that the algorithm is applied to the problem in Equations (2), when is a vertical block P-matrix of type and there exists a

such that

(6)

and there exists an such that.

Then in any succeeding stage of the scheme, the nonbasic related variable represented by will always be a basic related variable.

Proof: Without loss of generality, let. Then

and suppose.

The next step in the scheme would be to interchange with. Suppose in some succeeding stage of the scheme, we have for some

Suppose. Consider the ordered related -tuples associated with.

We will construct a representative submatrix of according to the following criteria:

Case 1: If, then let,

Case 2: For, if, find such that and.

Let. For, we have, and, for some, where is the minimum defined above.

If, this implies that. If, then. In either case, fix, where. Let

Since the components of and are chosen to correspond with the rows of, we have

Therefore,

or

and

We conclude that cannot be a P-matrix by Gale and Nakaido [18] . Therefore, does not equal the minimum subscript such that, for some. Therefore, the basic variable is not a candidate to be interchanged with in any succeeding step of the scheme for

such that the conditions of Equations (6) are met.

Theorem 6. If is a vertical block P-matrix of type, the algorithm when applied to Equations (2) will terminate with a solution in a finite number of steps. A related basic matrix that appears once in the scheme will not reappear in any succeeding steps.

Proof: If, then is a vertical block P-matrix of type, and by Theorem 5, we see that a solution will be found in at most steps. Also once a nonbasic variable becomes basic, it cannot become nonbasic in subsequent steps. Hence, a related basic matrix can appear at most one time in the course of the scheme.

Suppose and the theorem holds for all generalized linear complementarity problems such that is an vertical block P-matrix of type. Let be the unique solution of Equations (2).

Case 1: If, then by Lemma 1, is the unique solution to Equations (5). Since is a vertical block P-matrix of type, Theorem 5 applies and the scheme terminates in a finite number of steps with a solution. Any related basic matrix that appears once in the scheme will nor re-appear again. Let the sequence of related basic vectors that appear when the system is applied to be to, where

and and represent the basic and nonbasic variables of the unique solution to (5),.

When the scheme is applied to (2), is a related variable. The question of interchanging for some will not be considered in the scheme until we come upon such that

The first related basic and nonbasic vectors must be

for to. Lemma 4 and the fact that imply that are the basic and nonbasic variables. Therefore, the theorem applies to the algorithm if.

Case 2: If and for some, then every related basic vector cannot be a solution to (2) since.

Apply the scheme to (5). By the induction process, we have a sequence of related basic vectors to, and if a basic matrix appears once in the scheme it does not reappear, is some finite number and are the related basic and nonbasic vectors associated with the unique solution to (5).

When we apply the scheme to (2), the first related basic and nonbasic vectors must be

for to. The hypothesis that leads to

and there exists an such that

The next related basic vector to appear in the scheme would be

where the basic variables associated with are the same basic variables associated with for, and represents the variable. The related nonbasic variables would be

Let. Let B be the associated related basic matrix and let. Let D be the associated related nonbasic matrix.

That is, those columns associated with the components of t. Then

Multiplying both sides of the above equation on the left by, we have

is a vertical block P-matrix of type, since it is the result of a sequence of principal pivots on N. The generalized linear complementarity problem with respect to is:

For, find such that

(7)

By our assumptions, (7) has a unique solution in which. If, then the unique solution to (7) is and. The subsequent related basic vectors for solving (2) are exactly those related basic vectors which will be obtained by applying the scheme to (7) with as the initial related basic vector.

We showed in Case 1 that a generalized linear complementarity problem like (7) with unique solution and is solved by applying the scheme to (7) and a solution will be obtained in a finite number of steps without a related basic matrix appearing more than once. All these basic matrices will have as a basic variable of the nth block of basic variables and will be nonbasic.

If, we apply the scheme to (7). When applying the scheme to (7), we can argue just as we did when we first applied the scheme to (2). If our transformed system (7) has the unique solution such that, then after steps in the scheme, we arrive at a related basic and nonbasic vector and, respectively, where

and there exists an

By the way the scheme continues, we must eventually reach a transformed system

that will have as its unique solution and. Theorem 5 assures us that a related basic matrix that appears once in the scheme will not re-appear in the scheme. This proves that the theorem must hold if the scheme is applied to (2). Since the theorem is true for, it holds for all n.

4. Discussion and Conclusions

The vertical generalized linear complementarity Problem is very general and useful; and it can be applied to many problems in engineering, science, and economics. As such, it may be compared with systems of linear equations, the eigenvalue problem, and linear programming. Thus, it is desirable to have reliable and fail-safe algorithms to obtain a solution. Under the assumption of vertical block P-matrix, such a solution exists and is unique. Thus the algorithm takes the input data and returns, the unique solution. When this occurs, a mapping is defined and this mapping can be used to explore the nature of the VGLP and gain many insights which the researcher desires. An example of this is illustrated in the paper by Oh [10] .

Further research might involve investigating the performance of the algorithm under random input data, measuring the number of iterations taken on average, etc., and the number of arithmetic operations necessary to obtain a solution. These investigations are in lieu of knowledge of a fixed number of iterations and arithmetic operations.

An alternative approach might be to examine a limited set of solutions (say 10 - 50) using a restricted set of points in order to answer some specific questions. This may represent a set of “what if” questions and may satisfy the requirement of this type of study. It is easy to see the appeal of this type of analysis.

Finally, one may envision the algorithm in use as an embedded system, in a vehicle, an industrial machine or a video game. It is quite likely that the model mentioned in Oh [10] would be used in such applications with models of motion, contact (or collision), fluid flow, cooling, etc. In all these cases, the use of direct algorithm will provide efficient, reliable solutions which are necessary for the application of the system in which it is embedded.

The direction of future research will be motivated by all of the above instances of the applications of the vertical generalized linear complementarity problem, and by the discovery of new application areas, which seems to be increasing, as the understanding of this problem continues to develop.

The direct algorithm presented in this paper has certain features not present in other algorithms. It converges in a finite number of steps, and each step consists of only a unique principal pivot. No anti-cycling device is necessary, even if there is degeneracy in the defining equations. Since the choice of pivot rule is discrete, rather than continuous (such as in the minimum ratio test), no ties are possible. If desired, the use of pre-existing linear algebra software enables the solution of the linear equations, which is required for each iteration of the algorithm.

Acknowledgements

The authors thank Professor James Brannan of Clemson University for his assistance with obtaining some of the resources used in this research.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Murty, K.G. (1974) Note on a Bard-Type Scheme for Solving the Linear Complementarity Problem. Opsearch, 11, 121-130.
[2]	Chakraborty, B. and Ebiefung, A.A. (2013) The Generalized Horizontal Linear Complementarity Problem. Journal of Mathematical Research, 5, 1-6.
[3]	Cottle, R.W. and Dantzig, G.B. (1970) A Generalization of the Linear Complementarity Problem. Journal of Combinatorial Theory, 8, 79-90. https://doi.org/10.1016/S0021-9800(70)80010-2
[4]	Lemke, C.E. (1968) On Complementary Pivot Theory. In: Dantzig, G.B. and Pinott, A.F., Eds., Mathematics of the Decision Sciences, America Mathematical Society, Providence, 1, 97-115.
[5]	Habetler, G.J. and Szanc, B.P. (1995) Existence and Uniqueness of Solutions for the Generalized Linear Complementarity Problem. Journal of Optimization Theory and Applications, 14, 103-116. https://doi.org/10.1007/BF02191738
[6]	Ebiefung, A.A. (1994) A Support Submatrix for the Generalized Linear Complementarity Problem. Applied Mathematics Letters, 7, 35-38. https://doi.org/10.1016/0893-9659(94)90090-6
[7]	Ebiefung, A.A. (2007) Existence Theory and Q-matrix Characterization for the Generalized Linear Complementarity Problem: Revisited. Journal of Mathematical Analysis and Applications, 329, 1421-1429. https://doi.org/10.1016/j.jmaa.2006.07.036
[8]	Ebiefung, A.A. and Kostreva, M.M. (1992) Global Solvability of Generalized Complementarity Problems and a Related Class of Polynomial Complementarity Problems. In: Floudas, C. and Pardalos, P., Eds., Recent Advances in Global Optimization, Princeton University Press, New Jersey, 102-124.
[9]	Ebiefung, A.A., Kostreva, M.M. and Ramanujam, V. (1997) An Algorithm to Solve the Generalized Linear Complementarity Problem with a Vertical Block Z-Matrix. Optimization Methods and Software, 7, 123-138. https://doi.org/10.1080/10556789708805648
[10]	Oh, K.P. (1987) The Formulation of the Mixed Lubrication Problem as a Generalized Nonlinear Complementarity Problem, Transactions of the ASME 85. Journal of Tribology, 47, 598-603.
[11]	Ebiefung, A.A. and Kostreva, M.M. (1993) The Generalized Leontief Input-Output Model and Its Application to the Choice of New Technology. Annals of Operations Research, 44, 161-172. https://doi.org/10.1007/BF02061065
[12]	Ebiefung, A.A. and Kostreva, M.M. (2003) Production Equilibrium Point in Multi-Unit Manufacturing Systems and the Vertical Linear Complementarity Problem. Annals of Operations Research, 124, 183-192. https://doi.org/10.1023/B:ANOR.0000004768.22040.55
[13]	Ebiefung, A.A., Kostreva, M.M. and Majumdar I. (2008) Disjunctive Programming and the Generalized Leontief Input-Output Model. Applied Mathematics and Computation, 198, 551-558. https://doi.org/10.1016/j.amc.2007.08.055
[14]	Ebiefung, A.A. and Isaac, I. (2012) An Input-Output Pollution Control Model and Product Selection. Journal of Mathematical Research, 4, 1-7. https://doi.org/10.5539/jmr.v4n5p1
[15]	Ebiefung, A.A. (2010) Choice of Technology, Industrial Pollution, and the Vertical Linear Complementarity Problem. Global Journal of Mathematical Sciences, 9, 113-120.
[16]	Kostreva, M.M. (1979) Cycling in Linear Complementarity Problems. Mathematical Programming, 16, 127-130. https://doi.org/10.1007/BF01582098
[17]	Ravindran, A. (1972) Algorithm 431: A Computer Routine for Linear and Quadratic Programming. Communications of ACM, 15, 818-820.
[18]	Gale, D. and Nikaido, H. (1965) The Jacobian Matrix and Global Univalence of Mappings. Mathematische Annalen, 159, 81-93. https://doi.org/10.1007/BF01360282