Hermite Solution of Bagley-Torvik Equation of Fractional Order

Tamour Zubair^1,2*, Marriam Sajjad³, Rehmatullah Madni², Amna Shabir²

¹Department of Applied Mathematics and Statics, Institute of Space and Technology, Islamabad, Pakistan.
²Department of Mathematics, University of Sargodah, Lyallpur Campus, Faisalabad, Pakistan.
³Department of Mathematics, University of Lahore, Lahore, Pakistan.

DOI: 10.4236/ijmnta.2017.63010                

Abstract

In this paper, a new methodology of fractional derivatives based upon Hermite polynomial is projected. The fractional derivatives are demonstrated according to Caputo sense. Hermite collocation technique is introduced to express the definite results of Bagley-Torvik Equations. The appropriateness and straightforwardness of numerical plan is presented by graphs and error tables.

Keywords

MAPLE 13, Bagley-Torvik Equations, Hermite Polynomials, Fractional Calculus

1. Introduction

Numerical analysis is the study of set of rules that use numerical estimation for the problems of mathematical analysis as distinguished from discrete mathematics. Fractional differential equations are operational and most effective tool to describe different physical phenomena such as rheology, diffusion processes, damping laws, and so on. Many technics have been delegated to solve differential equation of fractional order. Different structures are used to resolve the issues of nonlinear physical models of fractional orders like Finite element method [1] , Finite difference method [2] , differential transformation method [3] [4] , Adomian’s decomposition method [5] [6] [7] , variational iteration method [8] [9] [10] , Homotopy perturbation technique [11] , Zubair decomposition method (ZDM) [12] , (G’/G)-expansion method [13] , (U’/U)-expansion method [14] , U- expansion method [15] , Fractional sub numerical announcement method [16] [17] , Legendre wavelets technique [18] , Chebyshev wavelets framework [19] [20] [21] , Haar wavelets schema [22] , Legendre Method [23] , Chebyshev strategy [24] , Jacobi polynomial scheme [25] and collocation scheme [26] [27] [28] [29] . All the mentioned approaches have certain limitations like excessive computational work, less efficiency to tackle nonlinearity and divergent solution due to which many issues arise. All these disputes can be fixed with the help of orthogonal polynomials, which is a vital thought in close estimation and structures. These orthogonal polynomials are the reason of powerful strategies of spectral methods [30] [31] [32] . Starting late, Khader [33] displayed a capable numerical procedure for enlightening the fractional order physical problems using the Chebyshev polynomials. In the [34] two Chebyshev spectral frameworks for measuring multi-term fractional problems are displayed. The author (Tamour Zubair) devolve a new wavelets algorithm to construct the numerical solution of nonlinear Bagley-Torvik equation of fractional order which will have less computational works, straight forward and better accuracy as compare to the existing technique. It is to be emphasized that proposed algorithm is tremendously simple but highly effective Moreover, this new pattern is proficient for reducing the computational work to a tangible level while still retaining a very high level of accuracy.

2. Basic Definitions

Fractional Calculus [35] - [40]

We give some basic definitions and properties of the fractional calculus theory which are used further in this paper.

Definition 1. A real function 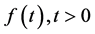is said to be in the space 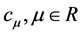if there exists a real number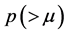, such that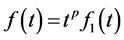, where 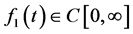, and it is said to be in the space iff.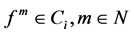

Definition 2. The Riemann-Liouville fractional integral operator of order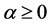, of a function 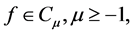is defined as

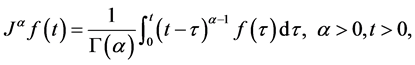
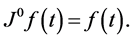
Properties of the operator 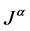can be found in literature, we mention only the following: For and: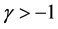

1)

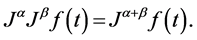
2)

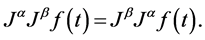
3)

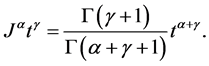
The Riemann-Liouville derivative has certain drawbacks when trying to model real-world processes with fractional differential equations. Therefore, we shall introduce a improved fractional differential operator 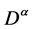proposed by.

Definition 3. The fractional derivative of in the Caputo sense is defined as

for. For the Caputo’s derivative we have is a constant,

We use the ceiling function to denote the smallest integer greater than or equal to, and. Recall that for, the Caputo differential operator coincides with the usual differential operator of integer order.

3. Bagley-Torvik Equations

Bagley-Torvik equation assumes an extremely vital part to study the performance of different material by application of fractional calculus [40] [41] . It has increased its significance in many fields of industrial and applied sciences. Precisely, the equation with 1/2 order derivative or 3/2 order derivative can be model the frequency dependent damping materials. The summed up form of Bagley-Torvik equation is given

(1)

with initial condition

with boundary condition at, for, is given by

where is the nonlinear operator of the equation, is unknown function. and are the constant coefficients, T is the constant representing the span of input in close interval [0,T], and are contents. When we have

where is mass of the rigid plate, is stiffness of the spring, S is the area of plate immersed in Newtonian fluid, is the velocity, and is the fluid density then equation (1) represents the motion of large thin plate in a Newtonian fluid [39] . Similarly, linearly damped fractional oscillator with the damping term

has the fraction derivative.

Further, we will discuss mathematical modeling of BT equation with feed-for- ward artificial neural network. The solution of the fractional differential equa-

tion along with its arbitrary order derivative can be approximated by the following continuous mapping as a neural network methodology [41] [42] [43] [44] :

where and are bounded real valued adaptive parameters, h is the number of neurons and is the active function taken as exponential function.Fractional differential equation neural networks (FDN-NNs) can be approximate as

for, we getUsing Definition 4, for, we get

Figure 1. FDE-NN architecture of Bagley-Torvik equation.

The mathematical model can be the linear combinations of the networks represented above. The FDE-NN architecture formulated for Bagley-Torvik equation can be seen in Figure 1. It is clear that the solution can be approximated with subject to finding appropriate unknown weights.

4. Hermite Polynomials [45]

It is classical orthogonal polynomials play very important role in probability. It has wide applications in numerical analysis as finite element methods as shape functions for beams. They are also applicable in physical quantum theory. Hermite polynomials are categorized into two kinds

The Probabilists Hermite polynomials are the solutions of

where and is a constant, with the boundary conditions that

should be polynomially bounded at infinity. The above equation can be written in the form of eigen value problem

solutions are the Eigen functions of the differential operator. This equation is called Hermite equation, although the term is also used for the closely related equation

whose solutions are the Physicists Hermites Polynomials, which is the second kind of Hermite polynomials.

The Hermite polynomials is given by

where

and also.

and the two branches of Hermite polynomial of degree, which are orthogonal with respect to weigh function.

Here we have.

Further we have orthogonality is given by

A function can be express in term of Hermite polynomials

where coefficients is given by

where.

5. Fractional Form of Hermite Polynomials [35] - [40]

The explicit formula of Hermites polynomials is

(1*)

where is given by

Further we have

(2)

where is given by

A function can be express in term of Hermite polynomials

(3)

where are Hermites polynomials. Using (1*)-(3) and definition of fractional derivative, we get the following

(4)

where and is given by and .

Note that only for, we have following

a) Methodology

Consider the multi order fractional differential equation (1) as

(5)

where is the unknown function, to be determined. The proposed technique for solving Equation (5) proceeds in the following three steps:

Step 1: According to the proposed algorithm we assume the following trial solution

(6)

where and.

where are Hermite polynomials of degree defined in Equation (6) and are unknown parameters, to be determined.

Step 2: Substituting Equation (6) into Equation (5), we get

Using (4) we have

(7)

Step 3: Further we Assume suitable collocation point for Equation (7). There- fore, we obtained system has equations and unknowns. Solving this system gives the unknown coefficients using Conjugate Gradient Method. Putting these constant into trial solution, we can obtained the approximate/exact solutions of linear/nonlinear fractional differential Equation (5).

b) Approximation by Hermite Polynomials [45]

Let us define and. The -orthogonal projection be the mapping and we have

Due to the orthogonality property, we can write it as

where are the constants in the following form

6. Numerical Simulation

In this section, we apply new algorithm to construct approximate/exact solutions fractional differential equation. Numerical results are very encouraging.

Case 1 In Equation (1), we take, , , , , ,. The close form solution is.

Consider the trial solutions for as

Using the trail solution into Equation (1) and proceed it according to Step 1 and Step 2, then we collocate it further to generate the system of equations. Solve the system of equations along with initial conditions, we get the values of constants

Finally, we get the approximate solution

which is exact solution.

Case 2 In Equation (1), we take, , , , , ,. The close form solution is.

Consider the trial solutions for as

Using the trail solution into Equation (1) and proceed it according to Step 1 and Step 2, then we collocate it further to generate the system of equations. Solve the system of equations along with initial conditions, we get the values of constants

Finally, we get the approximate solution

which is exact solution.

Case 3 In Equation (1), we take, , , ,. The close form solution is.

This equation can be simplify by using

Consider the trial solutions for as

Using the trail solution into Equation (1) and proceed it according to Step 1 and Step 2, then we collocate it further to generate the system of equations. Solve the system of equations along with initial conditions, we get the values of constants

Finally, we get the approximate solution

which is exact solution.

Case 4 In Equation (1), we take, , , , , , ,. The close form solution is.

Using the trail solution into Equation (1) and proceed it according to Step 1 and Step 2, then we collocate it further to generate the system of equations. Solve the system of equations along with initial conditions, we get the values of constants

Finally, we get the approximate solution

which is exact solution.

Case 5. In Equation (1), we take, , , , , , ,. The close form solution is.

The numerical solution is represented in Table 1 in case of and, while the error for various values of and are repre- sented in Table 2. There is a graphical comparison between exact and approximate solution represented in Figure 2.

Table 1. Numerical comparison between exact and approximate solution for deferent values of

Table 2. Numerical comparison between exact approximate solutions for different values of

Figure 2. Graphysical comparision between exact and approximted solution.

7. Conclusions

All the facts and findings of the paper are summarized as follow:

・ This paper provides novel study of Bagley-Torvik equations of fractional order in different situations by using newly suggested Hermite Polynomial scheme.

・ Implementation of this methodology is moderately relaxed and with the help of this suggested algorithm, complicated problems can be tackled.

・ It is to be highlighted that the suggested comparison gives attentive respond regarding some particular issues for values of M, which demonstrates viability of the proposed framework. Likewise, the reliability of the application provided this technique a more comprehensive suitability.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Deng, W. (2008) Finite Element Method for the Space and Time Fractional Fokker-Planck Equation. SIAM Journal on Numerical Analysis, 47, 204-226. http://epubs.siam.org/doi/abs/10.1137/080714130 https://doi.org/10.1137/080714130
[2]	Gao, G.H., Sun, Z.Z. and Zhang, Y.N. (2012) A Finite Difference Scheme for Fractional Sub-Diffusion Equations on an Unbounded Domain Using Artificial Boundary Conditions. Journal of Computational Physics, 231, 2865-2879. https://www.hindawi.com/journals/mpe/2012/924956/ https://doi.org/10.1016/j.jcp.2011.12.028
[3]	Momani, S., Odibat, Z. and Erturk, V.S. (2007) Generalized Differential Transform Method for Solving a Space- and Time-Fractional Diffusion-Wave Equation. Physics Letters A, 370, 379-387. https://www.mutah.edu.jo/userhomepages/shmomani/public.htm https://doi.org/10.1016/j.physleta.2007.05.083
[4]	Odibat, Z. and Momani, S. (2008) A Generalized Differential Transform Method for Linear Partial Differential Equations of Fractional Order. Applied Mathematics Letters, 21, 194-199. https://pdfs.semanticscholar.org/7250/38695674846cdbb7c5f5d2d9cbcb5f4e0fc9.pdf https://doi.org/10.1016/j.aml.2007.02.022
[5]	Hu, Y., Luo, Y. and Lu, Z. (2008) Analytical Solution of the Linear Fractional Differential Equation by Adomian Decomposition Method. Journal of Computational and Applied Mathematics, 215, 220-229. https://pdfs.semanticscholar.org/58a6/966afe30ccc2f7bbc6b 17319d6a3d1a663ba.pdf https://doi.org/10.1016/j.cam.2007.04.005
[6]	El-Sayed, A.M.A. and Gaber, M. (2006) The Adomian Decomposition Method for Solving Partial Differential Equations of Fractal Order in Finite Domains. Physics Letters A, 359, 175-182. https://www.researchgate.net/publication/223114291_The_A domian_decomposition_method_for_solving_partial_differential _equations_of_fractal_order_in_finite_domains https://doi.org/10.1016/j.physleta.2006.06.024
[7]	El-Sayed, A.M.A., Behiry, S.H. and Raslan, W.E. (2010) Adomian’s Decomposition Method for Solving an Intermediate Fractional Advection-Dispersion Equation. Computers & Mathematics with Applications, 59, 1759-1765. http://www.sciencedirect.com/science/article/pii/S0898122109005537 https://doi.org/10.1016/j.camwa.2009.08.065
[8]	Inc, M. (2008) The Approximate and Exact Solutions of the Space- and Time-Fractional Burgers Equations with Initial Conditions by Variational Iteration Method. Journal of Mathematical Analysis and Applications, 345, 476-484. http://www.sciencedirect.com/science/article/pii/S0022247X08003739 https://doi.org/10.1016/j.jmaa.2008.04.007
[9]	Odibat, Z. and Momani, S. (2009) The Variational Iteration Method: An Efficient Scheme for Handling Fractional Partial Differential Equations in Fluid Mechanics. Computers & Mathematics with Applications, 58, 2199-2208. http://www.sciencedirect.com/science/article/pii/S0898122109001436 https://doi.org/10.1016/j.camwa.2009.03.009
[10]	Wu, G.C. and Lee, E.W.M. (2010) Fractional Variational Iteration Method and Its Application. Physics Letters A, 374, 2506-2509. https://zulfahmed.files.wordpress.com/2015/06/2010-physic s-letters-section-a-general-atomic-and-solid-state-physics-37425.pdf https://doi.org/10.1016/j.physleta.2010.04.034
[11]	He, J.H. (2003) Homotopy Perturbation Method: A New Nonlinear Analytical Technique. Applied Mathematics and Computation, 135, 73-79. https://www.researchgate.net/publication/242791050_Homo topy_perturbation_method_A_new_nonlinear_analytical_technique https://doi.org/10.1016/S0096-3003(01)00312-5
[12]	Zubair, T., Hamid, M., Saleem, M. and Mohyud-Din, S.T. (2015) Numerical Solution of Infinite Boundary Integral Equations. International Journal of Modern Applied Physics, 5, 18-25. https://www.researchgate.net/publication/311202189_Nume rical_Solution_of_Infinite_Boundary_Integral_Equations
[13]	Bin, Z. (2012) (G’/G)-Expansion Method for Solving Fractional Partial Differential Equations in the Theory of Mathematical Physics. Communications in Theoretical Physics, 58, 623-630. http://ctp.itp.ac.cn/EN/article/downloadArticleFile.do?attachType=PDF&id=15873 https://doi.org/10.1088/0253-6102/58/5/02
[14]	Usman, M. and Mohyud-Din, S.T. (2013) Traveling Wave Solutions of 7th Order Kaup Kuperschmidt and Lax Equations of Fractional-Order. International Journal of Advances in Applied Mathematics and Mechanics, 1, 17-34. http://www.ijaamm.com/uploads/2/1/4/8/21481830/paper_2_sayed.pdf
[15]	Usman, M. and Mohyud-Din, S.T. (2014) U-Expansion Method for 5th Order Kaup Kuperschmidt and Lax Equation of Fractional Order. International Journal of Modern Mathematical Sciences, 9, 63-81. http://www.modernscientificpress.com/journals/ViewArticle. aspx?XBq7Uu+HD/8eRjFUGMqlRUFMGJSojFCd8JeYyjsMmViT RlEyTDVgYMCmavqTokhF
[16]	Alzaidy, J.F. (2013) Fractional Sub-Equation Method and Its Applications to the Space-Time Fractional Differential Equations in Mathematical Physics. British Journal of Mathematics & Computer Science, 3, 153-163. https://www.researchgate.net/publication/271263179_Fracti onal_Sub-Equation_Method_and_its_Applications_to_the_Space- Time_Fractional_Differential_Equations_in_Mathematical_Physics https://doi.org/10.9734/BJMCS/2013/2908
[17]	Alzaidy, J.F. (2013) The Fractional Sub-Equation Method and Exact Analytical Solutions for Some Nonlinear Fractional PDEs. American Journal of Mathematical Analysis, 1, 14-19. http://pubs.sciepub.com/ajma/1/1/3/
[18]	Jafari, H., Yousefi, S.A., Firoozjaee, M.A., Momani, S. and Khalique, C.M. (2011) Application of Legendre Wavelets for Solving Fractional Differential Equations. Computers & Mathematics with Applications, 62, 1038-1045. http://www.sciencedirect.com/science/article/pii/S0898122111003257 https://doi.org/10.1016/j.camwa.2011.04.024
[19]	Khader, M.M., El Danaf, T.S. and Hendy, A.S. (2013) A Computational Matrix Method for Solving Systems of High Order Fractional Differential Equations. Applied Mathematical Modelling, 37, 4035-4050. https://www.researchgate.net/publication/235916821_A_com putational_matrix_method_for_solving_systems_of_high_order_f ractional_differential_equations https://doi.org/10.1016/j.apm.2012.08.009
[20]	Zhu, L. and Fan, Q.B. (2012) Solving Fractional Nonlinear Fredholm Integro-Differential Equations by the Second Kind Chebyshev Wavelet. Communications in Nonlinear Science and Numerical Simulation, 17, 2333-2341. https://advancesindifferenceequations.springeropen.com.preview live.oscarjournals.springer.com/track/pdf/10.1186/s13662-017- 10856?site=advancesindifferenceequations.springeropen.com.pre viewlive.oscarjournals.springer.com https://doi.org/10.1016/j.cnsns.2011.10.014
[21]	Agarwal, N. (1953) A Propos d’unc Note de H4. Pierre Humbert, C. R. Se’ances Acad. Sci., 236, 2031-2032. http://jnus.org/pdf/1/2014/1/1038.pdf
[22]	Li, Y. and Zhao, W. (2010) Haar Wavelets Operational Matrix of Fractional Order Integration and Its Applications in Solving the Fractional Order Differential Equations. Applied Mathematics and Computation, 216, 2276-2285. http://dl.acm.org/citation.cfm?id=2641414 https://doi.org/10.1016/j.amc.2010.03.063
[23]	Khader, M.M. and Hendy, A.S. (2012) The Approximate and Exact Solutions of the Fractional-Order Delay Differential Equations Using Legendre Pseudo Spectral Method. International Journal of Pure and Applied Mathematics, 74, 287-297. http://www.ijpam.eu/contents/2012-74-3/1/1.pdf
[24]	Sweilam, N.H. and Khader, M.M. (2010) A Chebyshev Pseudo-Spectral Method for Solving Fractional Integro-Differential Equations. The ANZIAM Journal, 51, 464-475. https://www.cambridge.org/core/journals/anziam-journal/arti cle/div-classtitlea-chebyshev-pseudo-spectral-method-for-solvin g-fractional-order-integro-differential-equationsdiv/D54540C52 DE837C74F79EDB24A32FE71 https://doi.org/10.1017/S1446181110000830
[25]	Beheshti, S., Khosravian-Arab, H. and Zare, I. (2012) Numerical Solution of Fractional Differential Equations by Using the Jacobi Polynomials. Bulletin of the Iran Mathematical Society, 39, 6461-6470. http://bims.iranjournals.ir/article_947_b3ed3a5b2e22cf9386624a6699f3ff0d.pdf
[26]	Xu, C.-L. and Guo, B.-Y. (2002) Laguerre Pseudospectral Method for Non-Linear Partial Differential Equations. Journal of Computational Mathematics-International Edition, 20, 413-428. http://dergi.cumhuriyet.edu.tr/cumuscij/article/view/5000118841
[27]	Razzaghi, M. and Yousefi, S. (2001) Legendre Wavelets Method for the Solution of Nonlinear Problems in the Calculus of Variations. Mathematical and Computing Modelling, 34, 45-54. http://www.sciencedirect.com/science/article/pii/S0895717701000486
[28]	Khader, M.M. (2012) Introducing an Efficient Modification of the Homotopy Perturbation Method by Using Chebyshev Polynomials. Arab Journal of Mathematical Sciences, 18, 61-71. http://www.sciencedirect.com/science/article/pii/S131951661100051X https://doi.org/10.1016/j.ajmsc.2011.09.001
[29]	Khader, M.M., Sweilam, N.H. and Mahdy, A.M.S. (2011) An Efficient Numerical Method for Solving the Fractional Diffusion Equation. Journal of Applied Mathematics and Bioinformatics, 1, 1-12. http://www.scienpress.com/upload/JAMB/Vol%201_2_1.pdf
[30]	Hussaini, M.Y. and Zang, T.A. (1987) Spectral Methods in Fluid Dynamics. Annual Review of Fluid Mechanics, 19, 339-367. http://www.annualreviews.org/doi/abs/10.1146/annurev.fl.19.010187.002011 https://doi.org/10.1146/annurev.fl.19.010187.002011
[31]	Funaro, D. (1992) Polynomial Approximation of Differential Equations. Springer Verlag, New York, 8. http://www.springer.com/gb/book/9783662138786
[32]	Khader, M.M., El Danaf, T.S. and Hendy, A.S. (2012) Efficient Spectral Collocation Method for Solving Multi-Term Fractional Differential Equations Based on the Generalized Laguerre Polynomials. Fractional Calculus Application, 3, 1-14. http://naturalspublishing.net/files/published/vk2130l11wp11o.pdf
[33]	Khader, M.M. (2011) On the Numerical Solutions for the Fractional Diffusion Equation. Communications in Nonlinear Science and Numerical Simulations, 16, 2535-2542. http://www.ijpam.eu/contents/2013-84-4/1/1.pdf
[34]	Doha, E.H., Bahrawy, A.H. and Ezz-Eldien, S.S. (2011) Efficient Chebyshev Spectral Methods for Solving Multi-Term Fractional Orders Differential Equations. Applied Mathematical Modelling, 35, 5662-5672. http://naturalspublishing.net/files/published/vk2130l11wp11o.pdf https://doi.org/10.1016/j.apm.2011.05.011
[35]	Dalir, M. and Bashour, M. (2010) Applications of Fractional Calculus. Applied Mathematical Sciences, 4, 1021-1032. https://pdfs.semanticscholar.org/b9f3/cebf62c66c7bc06eab0 09aa1d60d70a19312.pdf
[36]	Schneider, K., Kevlahan, N.K.R. and Farge, M. (1997) Comparison of an Adaptive Wavelet Method and Nonlinearly Filtered Pseudospectral Methods for Two-Dimensional Turbulence. Theoretical and Computational Fluid Dynamics, 9, 919-206. https://link.springer.com/article/10.1007/s001620050040
[37]	Erdelyi, A. (1955) Higher Transcendental Functions, McGrawHill, New York. http://apps.nrbook.com/bateman/Vol3.pdf
[38]	Bagley, R.L. and Torvik, P.J. (1983) Fractional Calculus—A Different Approach to the Analysis of Viscoelastically Damped Structures. AIAA Journal, 21, 741-748. https://arc.aiaa.org/doi/abs/10.2514/3.8142 https://doi.org/10.2514/3.8142
[39]	Podlubny, I. (1999) Fractional Differential Equations, vol. 198 of Mathematics in Science and Engineering, Academic Press, San Diego. http://www.sciepub.com/reference/3051
[40]	Bagley, R.L. and Torvik, P.J. (1984) On the Appearance of the Fractional Derivative in the Behavior of Real Materials. Journal of Applied Mechanics, 51, 294-298. http://appliedmechanics.asmedigitalcollection.asme.org/article.aspx?articleid=1407517 https://doi.org/10.1115/1.3167615
[41]	Zahoor, M.A., Khan Raja, J.A. and Qureshi, I.M. (2010) Heuristic Computational Approach Using Swarm Intelligence in Solving Fractional Differential Equations. Proceedings of the 12th Annual Genetic and Evolutionary Computation Conference, Portland, 2023-2026. https://www.hindawi.com/journals/cin/2012/721867/ref/
[42]	Ray, S.S. and Bera, R.K. (2005) Analytical Solution of the Bagley Torvik Equation by Adomian Decomposition Method. Applied Mathematics and Computation, 168, 398-410. http://www.ijpam.eu/contents/2016-110-2/3/
[43]	Zahoor, R.M.A., Khan, J.A. and Qureshi, I.M. (2009) Evolutionary Computation Technique for Solving Riccati Differential Equation of Arbitrary Order. World Academy of Science, Engineering and Technology, 58, 531-536. https://scholar.google.com.pk/citations?view_op=view_citatio n&hl=en&user=z9xwIcMAAAAJ&citation_for_view=z9xwIcMA AAAJ:WF5omc3nYNoC
[44]	Raja, M.A.Z., Khan, J.A. and Qureshi, I.M. (2010) Evolutionary Computational Intelligence in Solving the Fractional Differential Equations. Proceedings of the Asian Conference on Intelligent Information and Database Systems, Hue City, 24-26 March 2010, 231-240. https://link.springer.com/chapter/10.1007/978-3-642-12145-6_24 https://doi.org/10.1007/978-3-642-12145-6_24
[45]	Bojdi, Z.K., Ahmadi-Asland, S. and Aminataei, A. (2013) Operational Matrices with Respect to Hermite Polynomials and Their Applications in Solving Linear Differential Equations with Variable Coefficients. Journal of Linear and Topological Algebra, 2, 91-103. https://doaj.org/toc/2345-5934