Limit Treatment of Space-Time Foam Calculations If Non Pathological Big Bang Singularity Is Accessible to Modified Einstein Equations ()
1. Introduction
This article is to investigate what happens physically if there is a non pathological singularity.
At the start of space-time, i.e. no reason to have a minimum nonzero length, the reasons for such a proposal come from [1] by Stoica who may have removed the reason for the development of Planck’s length as a minimum safety net to remove what appears to be unavoidable pathologies at the start of applying the Einstein equations at a space-time singularity. What shows is unavoidable collapse of the usual assumptions of the inter relationships of the number of operations in space-time, of the number of bits, and also of the average energy per bit
of space time. We will work on the assumption of 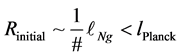 and
and
only invoke the  value to make an extreme point as to back up assertions made earlier, without calculations in a prior paper. Certain physics effects
value to make an extreme point as to back up assertions made earlier, without calculations in a prior paper. Certain physics effects
make themselves apparent well before 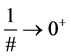 limit, and are commented upon
limit, and are commented upon
in this article.  in particular is remarked upon. This is a counterpart to Fjortoft theorem in Appendix I.
in particular is remarked upon. This is a counterpart to Fjortoft theorem in Appendix I.
2. Mach’s Principle as Initially Stated, in EW to Present Day Era. Preserving Planck’s Constant
We first of all review an earlier proposed Mach’s principle for the Gravitinos in the electro weak era, and then the 2nd modern day Mach’s principle, as organized by the author are as seen in [2] . This construction was used in an earlier article to argue in favor of a constant value of h bar, i.e. Planck’s constant. For the sake of review, we will state that the values in
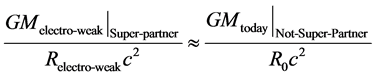 (1)
(1)
are really a statement of information conservation. i.e. the amount of information stored in the left hand side of (1) is the same as information as in the right hand side of (1) above. Here, M as in the electro weak era refers to M = N times m, where M is the total “mass” of the gravitinos, N the number of Gravitinos, and R for the electro weak as an infinitely small spatial radius. Whereas the Right hand side is for M for gravitons (not super partner objects) = N as the (number of gravitons) and m (the ultra-low mass of the graviton) in the right hand side of (1). This formula (1) should be compared with a change in entropy formula given by Lee [3] about the inter relationship between energy, entropy and temperature as given by
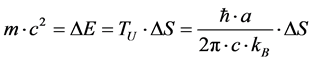 (2)
(2)
Lee’s formula is crucial for what we will bring up in the latter part of this document. Namely that changes in initial energy could effectively vanish if [1] is right, i.e. Stoica removing the non-pathological nature of a big bang singularity.
If the mass m, i.e. for gravitons is set by acceleration (of the net universe) and a change in entropy ![]() between the electroweak regime and the final
between the electroweak regime and the final
entropy value of, if ![]() for acceleration is used, so then we obtain
for acceleration is used, so then we obtain
![]() (3)
(3)
Then we are really forced to look at (1) as a paring between gravitons (today) and gravitons (electro weak) in the sense of preservation of information.
Having said this, we state that (3) above is based upon certain assumptions usually congruent with the quantum foam model [4] , and that what happens, especially to (3) is profoundly affected as we enter a regime for which
![]() . We follow Ng’s derivation [4] to make a cautionary point,
. We follow Ng’s derivation [4] to make a cautionary point,
while removing his worry about black holes, to state something about not only energy E, but also ![]() and by extension
and by extension![]() . As ρ changes
. As ρ changes
due to ![]() and
and![]() , then
, then![]() is also altered.
is also altered.
The point we make, is to go to the case of having ![]() means there would be no net expansion at all. If the universe were 4 dimensional and closed. We do not take the case of having no initial energy at the beginning of a closed universe as feasible or even realistic to refer to. The information theory implications though of what Stoica implies [1] as to bits and also holography need to be studied.
means there would be no net expansion at all. If the universe were 4 dimensional and closed. We do not take the case of having no initial energy at the beginning of a closed universe as feasible or even realistic to refer to. The information theory implications though of what Stoica implies [1] as to bits and also holography need to be studied.
What will determine the answer to this question is if ![]() goes to zero if
goes to zero if ![]() which happens if there is no minimum distance mandated to avoid the pathology of singularity behavior at the heart of the Einstein equations. In doing this, we avoid using the
which happens if there is no minimum distance mandated to avoid the pathology of singularity behavior at the heart of the Einstein equations. In doing this, we avoid using the ![]() situation, and instead refer to a nonzero energy, with
situation, and instead refer to a nonzero energy, with ![]() instead vanishing.
instead vanishing.
3. Review of Ng, [4] with Comments
First of all, Ng refers to the Margolus-Levitin theorem with the rate of operations
![]()
![]() . Ng wishes to avoid black-hole for- mation
. Ng wishes to avoid black-hole for- mation![]() . This last step is not important to our view point, but we
. This last step is not important to our view point, but we
refer to it to keep fidelity to what Ng brought up in his presentation. Later on, Ng refers to the ![]() with RH the Hubble radius. Next Ng refers to the
with RH the Hubble radius. Next Ng refers to the![]() . Each bit energy is
. Each bit energy is ![]() with
with ![]()
The key point as seen by Ng [4] and the author is in
![]() (4)
(4)
Assuming that E of the universe is not set equal to zero, which the author views as impossible, the above equation says that the number of available bits
goes down dramatically if one sets ![]() Also Ng writesentropy
Also Ng writesentropy
S as proportional to a particle count via N.
![]() (5)
(5)
We rescale ![]() to be
to be
![]() (6)
(6)
The upshot is that the entropy, in terms of the number of available particles drops dramatically if ![]() becomes larger.
becomes larger.
So, as ![]() grows smaller, as
grows smaller, as ![]() becomes larger
becomes larger
1) The initial entropy drops;
2) The number of bits initially available also drops.
The limiting case of (4) and (5) in a closed universe, with no higher dimensional embedding is that both would vanish, i.e. appear to go to zero if ![]() becomes very much larger.
becomes very much larger.
4. Examination of Mitra’s [5] Formation of Mass, Energy and Its Possible Effects on the Cosmological “Constant” Vacuum Energy
The prior result was to state that Avession’s [6] time varying ![]() in fact is a constant value, with no variation as due to alleged behavior represented by Mach’s principle as represented by (1) above. What will be done next will be to look at the role of energy of the universe, and what it says about quintessence. The construction comes from Mitra [5] and is adapted to what Beckwith did with the Machian universe relations [1] as given in (1) to (3) above. Mitra [5] in lieu of working with a FRLW universe, wrote
in fact is a constant value, with no variation as due to alleged behavior represented by Mach’s principle as represented by (1) above. What will be done next will be to look at the role of energy of the universe, and what it says about quintessence. The construction comes from Mitra [5] and is adapted to what Beckwith did with the Machian universe relations [1] as given in (1) to (3) above. Mitra [5] in lieu of working with a FRLW universe, wrote
![]() (7)
(7)
The density factor so parlayed in this treatment in the 1st equation in (7) was cited to have the relationship [5] by Mitra
![]() (8)
(8)
And the author put in, subsequently the following scaling factors
![]() (9)
(9)
In addition is the ![]() associated with the Hubble parameter and all that.
associated with the Hubble parameter and all that.
This leads to the energy value of the last equation of (7) to be written as
![]() (10)
(10)
Using a typical cubic solution for real valued roots, this comes out to be:
If we say that E = M, in the sense of the speed of light being set = 1, then
![]() (11)
(11)
This M though is for the total mass of the universe. But still we have
![]() (12)
(12)
In so many words, the parameter for quintessence goes to almost zero today, i.e.
![]() (13)
(13)
Question to ask is as follows. i.e. look at what the author derived
![]() (14)
(14)
This equation breaks down if![]() . What would replace it?
. What would replace it?
5. Does It Make Sense to Talk of Vacuum Energy If ![]() Is Changed to
Is Changed to![]() ? Only Answerable Straightforwardly If an Embedding Superstructure Is Assigned. Otherwise Difficult
? Only Answerable Straightforwardly If an Embedding Superstructure Is Assigned. Otherwise Difficult
The adaptation of the Mitra [5] relation for mass as given by (7) presupposes that there is a well-defined nonzero initial radius for cosmological evolution. We summarize what may be the high lights of this inquiry leading to the present paper as follows.
1) One could have the situation if ![]() of an infinite point mass, if there is an initial nonzero energy in the case of just four dimensions and no higher dimensional embedding even if [1] goes through verbatim. The author sees this as unlikely, but is prepared to be wrong. The infinite point mass construction is verbatim if one assumes a closed universe, with no embedding superstructure. Note this appears to nullify the parallel brane world construction author, in lieu of the manuscript sees no reason as to what would perturb this infinite point structure, so as to be able to enter in a big bang era. In such a situation, one would not have vacuum energy.
of an infinite point mass, if there is an initial nonzero energy in the case of just four dimensions and no higher dimensional embedding even if [1] goes through verbatim. The author sees this as unlikely, but is prepared to be wrong. The infinite point mass construction is verbatim if one assumes a closed universe, with no embedding superstructure. Note this appears to nullify the parallel brane world construction author, in lieu of the manuscript sees no reason as to what would perturb this infinite point structure, so as to be able to enter in a big bang era. In such a situation, one would not have vacuum energy.
2) The most problematic scenario. ![]() And no initial cosmological energy, i.e. this in a 4 dimensional closed universe. Then there would be no vacuum energy at all. Initially, a literal completely empties initial state, which is not held to be viable by Volovik [6] .
And no initial cosmological energy, i.e. this in a 4 dimensional closed universe. Then there would be no vacuum energy at all. Initially, a literal completely empties initial state, which is not held to be viable by Volovik [6] .
3) Finding that additional dimensions are involved, than just 4 dimensions may give credence to the authors speculation as to initial degrees of freedom reaching up to 1000, and the nature of a phase transition from essentially very low degrees of freedom, to over 1000 maybe in fact a chaotic mapping as speculated by the author in 2010 [7] .
The relevant template for examining such questions is given in Table 1 as printed below.
5) The meaning of Octonionic geometry prior to the introduction of quantum physics presupposes a form of embedding geometry and in many ways is similar to Penrose’s cyclic conformal cosmology speculation Note the following argument, as:
6) We are stuck with how a semi classical argument can be used to construct Table 1 below. In particular, we look at how Planck’s constant is derived, as in the electroweak regime of space-time, for a total derivative [9] [10]
![]() (15)
(15)
Similarly [9] [10]
![]() (16)
(16)
The A field so given would be part of the Maxwell’s equations given by [9] as, when ![]() represents a D’Albertain operator, that in a vacuum, one would have for an A field [9] [10]
represents a D’Albertain operator, that in a vacuum, one would have for an A field [9] [10]
![]() (17)
(17)
And for a scalar field ![]()
![]() (18)
(18)
![]()
Table 1. Time interval dynamical consequences do QM/WdW apply.
Following this line of thought we then would have an energy density given by, if ![]() is the early universe permeability [9]
is the early universe permeability [9]
![]() (19)
(19)
We integrate (19) over a specified E and M boundary, so that, then we can write the following condition namely [9] [10] .
![]() (20)
(20)
(20) would be integrated over the boundary regime from the transition from the Octonionic regime of space time, to the non Octonionic regime, assuming an abrupt transition occurs, and we can write, the volume integral as representing [9] [10]
![]() (21)
(21)
Our contention for the rest of this paper, is that Mach’s principle will be necessary as an information storage container so as to keep the following, i.e. having no variation in the Planck’s parameter after its formation from electrodynamics considerations as in (20) and (21). Then by applying [9] [10] we get ![]() formed by semi classical reasons and need to have Machs principle (1) to have the same value up to the present era.
formed by semi classical reasons and need to have Machs principle (1) to have the same value up to the present era.
![]() (Constant value) (22)
(Constant value) (22)
The question we can ask, is that can we have a prequantum regime com-
mencing for (20) and (21) for ![]() if
if![]() ? And a closed 4 di-
? And a closed 4 di-
mensional universe? If so, then what is the necessary geometrical regime of space-time so that the integration performed in (20) can commence properly? Also, what can we say about the formation of (21) above, as a number, ![]() gets
gets
larger and larger, effectively leading to![]() ? We need to know seriously
? We need to know seriously
how much space-time is needed to form (21) above? Do infinitesimal amounts of space-time suffice in order to fill in the following table as given below? If the
answer is no, then when ![]() leading to
leading to![]() ,
,
the semi classical derivation of (20) leading to (21) may not work. This is the ta-
ble to consider if ![]() and not zero. Also,
and not zero. Also,
with an Octonionic geometry regime which is a pre quantum state [11] .
In so many words, the formation period for ![]() is our pre-quantum regime. Table 1 could even hold if
is our pre-quantum regime. Table 1 could even hold if ![]() but that the 4 dimensional space-time exhibiting such behavior is embedded in a higher dimensional template.
but that the 4 dimensional space-time exhibiting such behavior is embedded in a higher dimensional template.
6. Having Not![]() , But
, But ![]() Growing Smaller, as
Growing Smaller, as ![]() Becomes Larger
Becomes Larger
If there is only an isolated 4 dimensional universe a situation for which:
1) The initial entropy drops;
2) The number of bits initially available also drops.
Then, we argue that dramatically cutting the initial entropy and also the bits would lead to real trouble as far as preserving the formation of ![]() as given in [9] [10] and may lead to difficulties in application of (1) especially if bits for a computation for expansion cannot be formed in a general way at the start of inflation. This uses the ideas in [11] and [12] precisely.
as given in [9] [10] and may lead to difficulties in application of (1) especially if bits for a computation for expansion cannot be formed in a general way at the start of inflation. This uses the ideas in [11] and [12] precisely.
7. If ![]() then If There Is an Isolated, Closed Universe, There Is a Messy Situation
then If There Is an Isolated, Closed Universe, There Is a Messy Situation
One does not have initial entropy, and the number of bits initially disappears.
Abandoning the idea of a completely empty universe, this unperturbed point of matter-energy appears to be a recipe for a static point with no perturbation, as may be the end result of applying Fjortoft theorem [13] to the thermodynamic potential as given in [13] , i.e. the non-definitive answer for fulfillment of criteria of instability by applying Fjortoft’s theorem [13] to the potential [11] leading to no instability as given by the potential given in [11] may lead to a point of space-time with no change, i.e. a singular point with “infinite” mass which does not change at all.
8. Can an Alternative to a Minimum Length Be Put in? Consider the Example of Planck Time as the Minimal Component, Not PLANCK Length
From J. Dickau, the following was given to the author, as a counter part as to how to view thresholds as to how a Mandelbrot set may pre select for critical behavior different from what is being pre supposed in this manuscript [14] .
Dickau writes:
“If we examine the Mandelbrot Set along the Real axis, it informs us about behaviors that also pertain in the Quaternion and Octonic case-because the real axis is invariant over the number types. If numbers larger than 0.25 are squared and summed recursively (i.e. ?z = z2 + c) the result will blow up, but numbers below this threshold never get to infinity, no matter how many times they are iterated. But once space-like dimensions are added i.e. an imaginary component- the equation blows up exponentially, faster than when iterated”.
Dickau concludes:
“Anyhow there may be a minimum (space-time length) involved but it is probably in the time direction”.
This is a counter pose to the idea of minimum length, i.e. the idea being a replacement for what the author put in here: looking at a beginning situation with a crucial parameter ![]() even if the initial time step is “put in by hand”. First of all, look at [4] , if E is M, due to setting c = 1, then
even if the initial time step is “put in by hand”. First of all, look at [4] , if E is M, due to setting c = 1, then
![]() (23)
(23)
Everything depends upon the parameter ![]() which can go to zero. The choice as to
which can go to zero. The choice as to ![]() going to zero, or not going to zero will be conclusion of our article.
going to zero, or not going to zero will be conclusion of our article.
We have to look at what (23) tells us, even if we have an initial time step for which time is initially indeterminate, as given by a redoing of Mitra’s g00 formula [4] which we put in to establish the indeterminacy of the initial time step if quantum processes hold.
![]() (24)
(24)
What Dickau is promoting is, that the Mandelbrot set, if applicable to early universe geometry, that what the author wrote, with
![]() potentially going to zero, is less im-
potentially going to zero, is less im-
portant than a minimum time length. To which the author states, if Dickau is correct as to applicability of the Mandelbrot set, that he, the author is happily corrected, but he also thinks that the Mandelbrot set is a beautiful example of the fungability of space-time metrics used. i.e. how one sets the initial space-time potential is to determine the correctness of the Mandelbrot set. i.e. the [13] reference, as given, by Padmanabhan appears not to have a Mandelbrot set, in its thermodynamic potential. The instability issue is reviewed in Appendix II. For those who are interested in the author’s views as to lack proof of instability. It uses [13] which the author views as THE reference as far as thermodynamic potentials and the early universe.
9. We Need to Reconsider the Role of Quantum Gravity Models at the Onset of Inflation
We are stuck in all Quantum gravity models as of putting in an initial time step “by hand” so to speak which raises fundamental issues of what would form an initial time step in Quantum gravity. How the transition from the left to the right hand side of (22) occurs is crucial and it comes about because of a transition from Octonionic geometry to quantum accessible and analyzable flat space geometry.
1) Having not![]() , but
, but ![]() grows smaller, as
grows smaller, as ![]()
becomes larger leads to, if there is only an isolated 4 dimensional universe a situation for which:
The initial entropy drops;
And the number of bits initially available also drops.
We argue that dramatically cutting the initial entropy and also the bits would lead to real trouble as far as preserving the invariance of ![]() [15] .
[15] .
2) If ![]() then if there is an isolated, closed universe, one does not have initialentropy, and the number of bits initially disappears. i.e. in lieu of [11] and [13] there may be no perturbation from an infinite point of space-time which remains invariant.
then if there is an isolated, closed universe, one does not have initialentropy, and the number of bits initially disappears. i.e. in lieu of [11] and [13] there may be no perturbation from an infinite point of space-time which remains invariant.
10. Conclusions
1) The universe if ![]() [1] and if it is an isolated system, i.e. not as embedded in higher dimensions as referred to in [16] may have no bits, or computations as thought of by Ng [4] . This would be in tandem with the author’s conclusion that one would have an initial infinite point mass and no evolution, and no generation of entropy.
[1] and if it is an isolated system, i.e. not as embedded in higher dimensions as referred to in [16] may have no bits, or computations as thought of by Ng [4] . This would be in tandem with the author’s conclusion that one would have an initial infinite point mass and no evolution, and no generation of entropy.
2) If ![]() [1] but the universe is embedded in a higher dimensional system, as given by [16] , then there is no reason to say there are no bits, or computations, and the universe will continue to evolve with entropy as a byproduct of that evolution.
[1] but the universe is embedded in a higher dimensional system, as given by [16] , then there is no reason to say there are no bits, or computations, and the universe will continue to evolve with entropy as a byproduct of that evolution.
3) The universe if one does not have![]() , i.e. if [1] does not hold, then there will be bits, entropy being generated, and also loop quantum gravity and quantum measures [17] so long as the minimum
, i.e. if [1] does not hold, then there will be bits, entropy being generated, and also loop quantum gravity and quantum measures [17] so long as the minimum ![]() Planck length grid exists. The reacceleration of the universe commences as given in [18] due to DE being the same as vacuum energy. The author in Appendix III gives a derivation as to how the DE will be put in, via branes, which holds for both 8b and 8c , as a to be proven sideline.
Planck length grid exists. The reacceleration of the universe commences as given in [18] due to DE being the same as vacuum energy. The author in Appendix III gives a derivation as to how the DE will be put in, via branes, which holds for both 8b and 8c , as a to be proven sideline.
Acknowledgements
This work is supported in part by National Nature Science Foundation of China Grant No. 11375279.
Appendix I. Fjortoft Theorem
A necessary condition for instability is that if ![]() is a point in space-time for
is a point in space-time for
which ![]() for any given potential
for any given potential![]() , then there must be some value
, then there must be some value ![]()
in the range ![]() such that
such that
![]() (1)
(1)
For the proof, see [12] and also consider that the main discussion is to find instability in a physical system which will be described by a given potential![]() . Next, we will construct in the boundary of the EW era, a way to come up with an optimal description for
. Next, we will construct in the boundary of the EW era, a way to come up with an optimal description for ![]()
Appendix II. Constructing an Appropriate Potential for Using Fjortoft Theorem in Cosmology for the Early Universe Cannot Be Done. We Show Why
To do this, we will look at Padamanabhan [12] and his construction of (in Dice 2010) of thermodynamic potentials he used to have another construction of the Einstein GR equations. To start, Padamanabhan [5] wrote
If ![]() is a so called Lovelock entropy tensor, and
is a so called Lovelock entropy tensor, and ![]() a stress energy tensor
a stress energy tensor
![]() (1)
(1)
We now will look at
![]() (2)
(2)
So happens that in terms of looking at the partial derivative of the top (1) equation, we are looking at
![]() (3)
(3)
Thus, we then will be looking at if there is a specified ![]() for which the following holds.
for which the following holds.
![]() (4)
(4)
What this is saying is that there is no unique point, using this ![]() for which (4) holds. Therefore, we say there is no official point of instability of
for which (4) holds. Therefore, we say there is no official point of instability of ![]() due to (3). The Lagrangian structure of what can be built up by the potentials given in (3) with respect to
due to (3). The Lagrangian structure of what can be built up by the potentials given in (3) with respect to ![]() mean that we cannot expect an inflection point with respect to a 2nd derivative of a potential system. Such an inflection point designating a speed up of acceleration due to DE exists a billion years ago [19] . Also note that the reason for the failure for (4) to be congruent to Fjoroft’s theorem is due to
mean that we cannot expect an inflection point with respect to a 2nd derivative of a potential system. Such an inflection point designating a speed up of acceleration due to DE exists a billion years ago [19] . Also note that the reason for the failure for (4) to be congruent to Fjoroft’s theorem is due to
![]() (5)
(5)
Appendix III. Modifying a Parallel Brane-Anti Brane Argument to Obtain Massive Gravitons
Part I, of Appendix III. We come into this situation if, as in applying Fjorofts theorem, that we find Appendix II, Equation (5), holds, and then if so, we have to find another way to induce vacuum energy.
What (5), appendix II tells us is that there is an embedding structure for early universe geometry, some of which may take the form of the following diagram.
Part II of Appendix III. Working with a way to achieve energy injection into the universe, without appealing to Fjortoft theorem for alleged instabilities starting from Padmanabhan thermodynamic potential terms
Padmanabhan [13] introduced the following discussion as to entropy, namely starting with energy, we have
![]() (1)
(1)
And the n value as in (7) is given by
![]() (2)
(2)
where ![]() is a so called Lovelock entropy tensor, and
is a so called Lovelock entropy tensor, and ![]() a bi normal on the codimension −2 cross section, and then entropy is stated to be
a bi normal on the codimension −2 cross section, and then entropy is stated to be
![]() (3)
(3)
The end result, is that energy is induced via the temperature![]() , while [13]
, while [13]
![]() (4)
(4)
Also, the change in n can be given by, if ![]() is the Planck’s length value [5]
is the Planck’s length value [5]
![]() (5)
(5)
Looking at (9) and (11) we state that the change in number count given in (4) is really a holographic surface phenomena, with N defined [13]
![]() (6)
(6)
The upshot is that we can, as implied by Ng [4] easily reference a change in entropy via [4]
![]() (7)
(7)
While having a change in n as due to a change in the spatial surface of space-time as given in (6), we have to realistically infer that the local acceleration temperature (4) is from another pre universe construction and that local instability is ruled out by Appendix II, Equation (5). This leads us to ask as to what would be an acceptable way to form the formation of mass, i.e. say the mass of a graviton, via external factors introduced into our universe prior to the electroweak era, in cosmology. To do that, look at if there are two branes on the ![]() space-time so that with one moving and one stationary, we can look at Figure 1 as background as to introduce such external factors in our present space-time universe during its initial expansion phase
space-time so that with one moving and one stationary, we can look at Figure 1 as background as to introduce such external factors in our present space-time universe during its initial expansion phase
Part III, of Appendix III: Fall out from adopting Figure 1 and that due to no instability in the Padamanabhan supplied potentials. i.e. a way to obtain graviton mass via a root finding method.
Using [16] what we find is that there are two branes on the ![]() space-time so that with one moving and one stationary, we can look at Figure 1 which is part of the geometry used in the spatial decomposition of the differential operator acting upon the
space-time so that with one moving and one stationary, we can look at Figure 1 which is part of the geometry used in the spatial decomposition of the differential operator acting upon the ![]() Fourier modes of the
Fourier modes of the ![]() operator [16] . As given by [16] , we have that
operator [16] . As given by [16] , we have that
![]() (8)
(8)
Using [16] the solution to (14) above takes the form of having
![]() (9)
(9)
![]() is a polarization tensor, and the function
is a polarization tensor, and the function ![]() is a 2nd order Bessel function [20] . A generalization offered by Durrer et al. [16] leads to
is a 2nd order Bessel function [20] . A generalization offered by Durrer et al. [16] leads to
![]() (10)
(10)
With the factor of ![]() coming in due to a boundary condition
coming in due to a boundary condition
upon the wall of a brane put in, i.e. looking at [16] . With the right hand side of (10) due to a domain wall tension of a brane.
![]() (11)
(11)
This will be in our example set as not equal to zero, in the right hand side, but equal to an extremely small parameter, namely
![]() (12)
(12)
With this turned into
![]() (13)
(13)
The right hand side of (13) represents very small brane tension, which is understandable. Then using [16] [20] , i.e.
![]() (14)
(14)
And
![]() (15)
(15)
The upshot is, that afterwards,
![]() (16)
(16)
Should the term
![]() (17)
(17)
Then, (17) is acting much as in [16] , whereas, one is recovering a simple numerical exercise as to obtain a suitable solution as given by (18), and (19) due to [3] where the domain tension of the brane vanishes. The novelty as to this approach given in (17) is to obtain a time dependent behavior of the mass of the graviton,
![]() (18)
(18)
Needless to say, (16) can only be solved for, numerically, i.e. fourth order polynomial solutions for quartic equations still give over simplified dynamics, especially if (18) holds, and makes things more complicated. This is all being done to keep fidelity with respect to [16] , as a possible feature of brane world dynamics as reflected in [16] , as well as certain issues brought up in [8] as to what is a semi classical argument can obtain a usually quantum result. If this semi classical result is true, it has profound implications for [21] , and [22] which are held to be M theory results with no classical analogues.
First of which is [19] . In it, important to the idea of R squared gravity having the consequence of a removal of early space-time singularities. The main result is in the quote that
“A non-singular early cosmology is proposed, where, adding a nonlinear electrodynamics Lagrangian to the high-order action, a bouncing is present and a power-law inflation is obtained. In the model the Ricci scalar R works like an inflaton field.”
We will search for a similar identification in our future followups as to the importants of the Ricci scalar.
Secondly is [23] and [24] . [23] outlines the program of identifying electromagnetic contributions to a non singular dense state of initial space-time matter-energy, and [24] by Corda et al. specifically uses in its quote that:
“Such analysis will be improved by applying the Oppenheimer-Volkoff equation to the black hole case. At the end, fixed the radius of the star, the final density depends only on the introduced quintessential density term ργ and on the mass.”
NLED identifies inputs for aquintessential density term ργ and we will be examining if our agument given in the text has any commonality with the Oppenheimer-Volkoff equation in a future update to our research endeavor.
![]()
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact jhepgc@scirp.org