1. Introduction
In the design of foundations and geotechnical structures it is essential to predict soil behavior under different loading conditions. In the last decade finite element analysis (FEA) has become a widely spread tool for predicting soil behavior. Much research has been carried out to improve the ability of simulating the behavior of different soils and a number of new constitutive models have been developed. Another important aspect when modeling geotechnical problems is the interaction between soil and structure, which can have a large influence on the structural design [1] .
Since first introduced by Hughes et al. in [2] , isogeometric analysis (IGA) has been used for a broad number of engineering problems, ranging from analysis of fluid-structure interaction [3] to analysis of shells [4] . Some of the areas where isogeometric analysis has shown to be advantageous compared to the standard finite element analysis are also of interest in geotechnics. One example is the simulation of fluid flow through porous media, where the higher-order basis functions of IGA lead to continuous pressure gradients over element boundaries ensuring local mass conservation, [5] and [6] . The basic idea behind isogeometric analysis is to use splines as basis functions for computational analysis [2] . Originally the purpose was to use the geometry from the Computer Aided Geometric Design (CAGD) software’s also for analysis and consequently reduce the time required to recreate models for analysis. However, the use of spline basis functions proved to have numerical benefits compared to the standard Lagrangian basis-functions used in FEA [7] [8] . Initially the IGA framework suffered from the lack of a method for local refinement, frequently sought during analysis. To overcome this initial drawback, a number of methods have been developed to introduce local refinements within the IGA framework, where T-splines [9] or Hierarchical NURBS [7] [10] are the most widely used methods. The higher- order smoothness of the basis functions in IGA also opens up the possibilities of using quadrature rules evaluated on element boundaries reducing the total number of quadrature points [2] [7] . Another interesting possibility within the IGA framework is the use of isogeometric collocation methods, a one-point quadrature rule that reduces the computational cost of analysis [11] . Since collocation methods are based on the discretization of the strong form of the partial differential equations, it would be suitable for the isogeometric concept. The use of isogeometric collocation has shown potential to increase the computational efficiency of the isogeometric framework, outperforming both the standard Galerkin form of isogeometric analysis and standard C0 finite element analysis with regard to computational costs [7] . As pointed out by Nguyen et al. [12] for non- linear analysis the numerical error strongly depends on the integration scheme and the order of the Non-Uniform Rational B-splines (NURBS) basis functions. To evaluate the isogeometric framework for geotechnical applications, it is interesting to assess how the isogeometric framework performs for soil plasticity. For simplicity and for setting up the numerical framework we restrict our self to quadratic NURBS basis functions in this work. As soil typically show strong plastic flow under hydrostatic pressure, special B-bar methods are not necessary in our work, see [13] for a discussion of these methods in the case of nearly incompressible material behavior.
In this work we have evaluated how isogeometric analysis performs compared to the conventional finite element method for soil plasticity in two and three dimensions. The focus of the work is to evaluate the convergence behavior and mesh size dependencies for isogeometric analysis and to compare them with results from conventional FEA. To provide a background, we start with outlining the basic concepts of isogeometric analysis, introducing the definitions of B- splines and NURBS that are used as basis or shape functions in this work. We later continue with the basic governing equations for elasto-plasticity followed by a brief recapitulation of the Drucker-Prager constitutive equations. The paper is concluded with two- and three-dimensional numerical examples, comparing the results to conventional finite element analysis.
2. Isogeometric Analysis
The fundamental idea behind IGA is to employ the same basis functions for both geometrical discretization and analysis. Herein lays also the most profound difference between IGA and standard FEA, where isogeometric analysis utilizes the basis functions from CAGD, capable of representing the exact geometry also for analysis. Whereas, in conventional finite element analysis, the piecewise polynomials chosen to approximate the solution fields are also used to approximate the geometry [2] . The original reason to use the isogeometric analysis was to decrease the overall computational cost by removing the need to recreate the geometry and constructing a mesh for analysis. In this work we have analyzed the performance of IGA for soil plasticity using a NURBS-based isogeometric formulation. To give a brief introduction to the concept of IGA and to elucidate some of the differences between conventional FEA and IGA this section will review the basic concepts of isogeometric analysis. For a more extensive description the reader is referred to [2] .
2.1. Basic Concept of B-Splines
To get an overview of the concept of NURBS-based isogeometric framework used in this work we start by defining a B-spline curve. A B-spline curve is a linear combination of B-spline basis functions,  and a set of corresponding control points
and a set of corresponding control points .
.
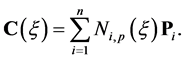 (1)
(1)
The B-spline basis functions Ni,p are constructed from a non-decreasing set of coordinates in the parameter space, written as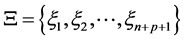 , where
, where  denotes the ith knot of the knot vector
denotes the ith knot of the knot vector , p indicates the order of the polynomial function and n represents the number of basis functions needed to construct a specific B-spline curve. With a given knot vector,
, p indicates the order of the polynomial function and n represents the number of basis functions needed to construct a specific B-spline curve. With a given knot vector,  , and a known polynomial order, p, it is possible to construct a B-spline basis function. For the case of (p = 0), the basis function take a piecewise constant shape given from
, and a known polynomial order, p, it is possible to construct a B-spline basis function. For the case of (p = 0), the basis function take a piecewise constant shape given from
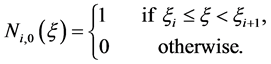 (2)
(2)
For 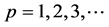 the B-spline basis function can be constructed by using the expression,
the B-spline basis function can be constructed by using the expression,
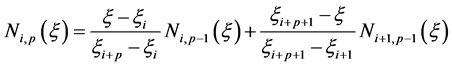 (3)
(3)
which is referred to as the Cox-de Boor formula, first presented in [14] and [15] . One example of a second order B-spline with three control points is illustrated in Figure 1. For polynomial degrees p < 2 the basis functions of IGA and conventional FEA take the same shape, however for p ≥ 2 they deviate in shape and support. By plotting the B-spline basis functions and Lagrangian basis functions over the parameter space some of the differences between IGA and conventional FEA are made visible, see Figure 2 and Figure 3. Figure 3 shows that for p ≥ 2, Lagrangian basis functions, the continuity varies between internal and corner- or end-nodes, whereas B-spline basis functions show a continuous and homogeneous pattern only shifted relative to each other and with Ni,p(ξ) ≥ 0. Another important aspect of spline basis functions, that distinguishes them from conventional FEA basis functions, is that each pth order function has p − 1 continuous derivatives across element boundaries.
![]()
Figure 1. A second order B-spline curve, C(ξ).
![]()
Figure 2. Representation of quadratic B-spline basis function with knot vector Ξ = {0, 0, 0, 1, 2, 3, 4, 5, 5, 5}.
![]()
Figure 3. Representation of quadratic Lagrangian basis function.
2.2. NURBS Representation
One issue that arises when using B-spline, is that not all types of geometries can be represented exactly using polynomial functions. To overcome this problem rational B-splines were introduced by Versprille in [16] . This generalization of B- splines is constructed by introducing a non-negative weight, wi, to each control point and making use of the definition of rational functions as the ratio of two polynomials [17] . A NURBS body in Rd can be obtained by projective transformation of a B-spline body in Rd + 1, where the weights, wi, are the d + 1 components of projective control points. Non-Uniform Rational B-splines (NURBS) are today standard in many CAGD software’s and the fast and stable algorithms make them a good choice also for analysis. To construct NURBS basis functions one can make use of the basis functions for B-splines,
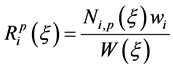 (4)
(4)
where W(ξ) is called a weighting function, defined as
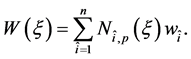 (5)
(5)
If wi = 1 for all i, then 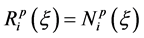 for all i. In fact, if the value of wi = a for all i then
for all i. In fact, if the value of wi = a for all i then 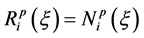 i.e., the
i.e., the 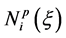 are special cases of
are special cases of ![]() where all the weights take the same value. Using the NURBS basis functions
where all the weights take the same value. Using the NURBS basis functions ![]() and their corresponding control points Pi, a piecewise NURBS curve, is constructed from
and their corresponding control points Pi, a piecewise NURBS curve, is constructed from
![]() (6)
(6)
To be able to perform two- and three-dimensional analysis, NURBS surfaces and bodies needs to be defined. This is done in a similar manner. A NURBS body is given by
![]() (7)
(7)
where the NURBS basis function, ![]() , is constructed from three sets of knot vectors, and their respective weighting functions
, is constructed from three sets of knot vectors, and their respective weighting functions![]() .
.
![]() (8)
(8)
where
![]() (9)
(9)
In the isogeometric framework the concept of elements is represented by the non-zero valued knot spans. This is illustrated in Figure 4, where a two dimensional plate is constructed from two knot vectors, a set of control points Pi,j and their corresponding weights wi,j. The geometry is constructed of one knot vector, Ξ = {0, 0, 0, 0.5, 1, 1, 1} in the direction of the arc of the hole and one knot vector, ![]() = {0, 0, 0, 1, 1, 1}, in the radial direction, thus creating a plate consisting of two elements. The element specific basis functions are constructed from the non- zero valued basis functions in the active knot span.
= {0, 0, 0, 1, 1, 1}, in the radial direction, thus creating a plate consisting of two elements. The element specific basis functions are constructed from the non- zero valued basis functions in the active knot span.
The number of active functions in a knot span is determined as![]() . For analysis the basis functions are evaluated at the chosen integration points of the parent element, see Figure 4(d). These element specific NURBS basis functions will be denoted
. For analysis the basis functions are evaluated at the chosen integration points of the parent element, see Figure 4(d). These element specific NURBS basis functions will be denoted ![]() in the reminder of this work.
in the reminder of this work.
![]()
Figure 4. A NURBS surface of the symmetric part of a plate with a circular hole constructed from two knot vectors, Ξ and![]() , a set of control points, Pi,j and their corresponding weights, wi,j. (a) shows the element mesh (b) the control net (c) the parameter space and basis functions (d) the parent element.
, a set of control points, Pi,j and their corresponding weights, wi,j. (a) shows the element mesh (b) the control net (c) the parameter space and basis functions (d) the parent element.
3. Equilibrium Conditions (Heading 3)
3.1. Strong and Weak Form
In this section we give a brief recapitulation of the strong and weak form of the equilibrium equations of the quasi-static balance of linear momentum. Let ui denote the displacement vector, then the infinitesimal strain tensor, εij, is defined as the symmetric part of the displacement gradient
![]() (10)
(10)
The governing strong form of the equilibrium equation is given as
![]() (11)
(11)
where fi is the body force. The strong form of the equilibrium equation is complemented by the essential and natural boundary conditions.
![]() (12)
(12)
![]() (13)
(13)
where gi and hi are known quantities on ∂Ωg and ∂Ωh. The variational or weak form of Equation (11) is formed by multiplying the governing equation with a test function vi and performing an integration by parts over the domain Ω
![]() (14)
(14)
The weak form of the problem is complemented by a constitutive relation
![]() (15)
(15)
with ![]() being a set of internal variables to describe the plastic behavior of the material. For a more detailed derivation of the weak form, the reader is tentatively referred to any of [18] or [19] .
being a set of internal variables to describe the plastic behavior of the material. For a more detailed derivation of the weak form, the reader is tentatively referred to any of [18] or [19] .
3.2. Discretization with Isogeometric Analysis
The main difference between conventional FEA and IGA are the basis functions used for discretization. In isogeometric analysis the same basis functions that are used to discretize the geometry are also used to solve for the approximate displacement field u. The only difference to conventional FEA is that the basis functions in IGA are element-specific. After solving the element-specific basis functions and their derivatives the procedure of establishing the stiffness matrix and internal force vector is identical to conventional FEA. The element specific basis function for each element is determined as the non-zero functions in the knot span. The displacement field for any given element can be solved using the element specific basis function![]() ,
,
![]() (16)
(16)
with ![]() the element displacements. The spatial derivatives of the displacement field can be approximated by taking the derivative of the element-spe- cific basis functions with respect to the physical coordinates x
the element displacements. The spatial derivatives of the displacement field can be approximated by taking the derivative of the element-spe- cific basis functions with respect to the physical coordinates x
![]() (17)
(17)
To obtain the derivatives of the basis functions with respect to the physical coordinates one must use the chain rule,
![]() (18)
(18)
with![]() . For a more straightforward implementation we rewrite the displacement field using a vector-matrix notation, i.e.,
. For a more straightforward implementation we rewrite the displacement field using a vector-matrix notation, i.e.,![]() . Where the matrix Ne contains the basis functions
. Where the matrix Ne contains the basis functions ![]() for each control point in support of an element
for each control point in support of an element
![]() (19)
(19)
In a similar manner we rewrite Equation (17) in matrix form,
![]() (20)
(20)
where the matrix Be is an operator mapping the element discrete displacements to the local strains.
![]() (21)
(21)
The test function vi can be discretized in the same manner as the displacement field. Introducing the relations above it is possible to rewrite Equation (14) in a residual format as
![]() (22)
(22)
with a the global unknown displacement vector. In this work we use a Newton-Raphson method to solve this system of nonlinear equations. The Jacobian matrix for the Newton-Raphson method reads
![]() (23)
(23)
with Dats the Voigt representation of the algorithmic tangent stiffness. In each Newton iteration we compute a displacement increment ∆a by solving the linear equation![]() . Afterwards, we update the displacement vector by a ← a + ∆a and stop the iteration if the residual r(a) < TOL with TOL a user given tolerance, e.g. TOL = 10−6.
. Afterwards, we update the displacement vector by a ← a + ∆a and stop the iteration if the residual r(a) < TOL with TOL a user given tolerance, e.g. TOL = 10−6.
4. Constitutive Model (Heading 4)
In this section we will give a brief recapitulation of the Drucker-Prager criterion and the theory of plasticity used to evaluate the influence of the NURBS-basis functions on the plastic strains for granular materials in this work.
4.1. Drucker-Prager Criterion
The Drucker-Prager criterion can be seen as a smooth approximation to the Mohr-Coulomb law and states that plastic yielding begins when the J2 and I1 invariants reach a critical combination. Although the Drucker-Prager formulation is a rather crude approximation of real soil behavior it has the benefit of being straightforward to implement and also lacks the singularities that exist in the yield function of the Mohr-Coulomb criterion. The yield function of the Drucker-Prager can be expressed using the first invariant of the stress tensor, I1, and the second invariant of the deviatoric stress, J2,
![]() (24)
(24)
which forms a circular cone in the principal stress space. The material parameters k and
, can be expressed in terms of the materials cohesion, ![]() and internal friction,
and internal friction, ![]() , by matching the Drucker-Prager criterion to the Mohr- Coulomb criterion,
, by matching the Drucker-Prager criterion to the Mohr- Coulomb criterion,
![]() (25)
(25)
where θ in represents the Lode angle. A positive sign in Equation (25) matches the Drucker-Prager cone to the inner edges of the Mohr-Coulomb surface. The matching to the Mohr-Coulomb criterion is illustrated in Figure 5.
4.2. Elasto-Plastic Constitutive Model
We assume a small strain setting and thus additively split the strain tensor ![]() into an elastic part
into an elastic part ![]() and a plastic part
and a plastic part ![]() as
as
![]() (26)
(26)
For geo-materials in general, associative flow rules for the plastic strain ![]() displays an excessive dilatant behavior. This can be avoided by using a non-
displays an excessive dilatant behavior. This can be avoided by using a non-
![]()
Figure 5. Projection of the Drucker-Prager criterion matched to the Mohr-Coulomb criterion on the deviator plane.
associative flow rule, that is, the potential function ![]() is not equal to the yield function
is not equal to the yield function![]() . In this work the potential function
. In this work the potential function ![]() is defined by replacing the angle of internal friction,
is defined by replacing the angle of internal friction, ![]() , with the angle of dilation, ψ, in Equation (25) forming
, with the angle of dilation, ψ, in Equation (25) forming
![]() (27)
(27)
The potential function is then written as
![]() (28)
(28)
At the surface of the Drucker-Prager yield function the evolution of the plastic strain is determined as,
![]() (29)
(29)
with ![]() the plastic multiplier and the derivative of the potential function is given from
the plastic multiplier and the derivative of the potential function is given from
![]() (30)
(30)
with Sij the deviatoric part of the stress tensor. Furthermore we assume a bi-li- near hardening model for the material cohesion ![]() and the angle of internal friction
and the angle of internal friction![]() , as depicted in Figure 6. Both hardening parameters are driven by the accumulated deviatoric plastic strain
, as depicted in Figure 6. Both hardening parameters are driven by the accumulated deviatoric plastic strain ![]() given by
given by
![]() (31)
(31)
The presented model is complemented by the loading/unloading conditions![]() and
and![]() . With the evolution equation for the plastic strain and the just described hardening model at hand we get the set of internal variables
. With the evolution equation for the plastic strain and the just described hardening model at hand we get the set of internal variables
![]()
Figure 6. Bi-linear strain dependent hardening.
for our plasticity model as![]() , see also Equation (15). For the numerical integration of the constitutive evolution equations we use a standard Euler backward scheme. The reader is referred to ( [20] , Sec. 7.2) which gives a detailed description of the numerical implementation procedure and also the format of the algorithmic tangent stiffness Dats. We like to mention that at the apex of the yield surface cone, the return vector is contained by a complementary cone, illustrated in Figure 7, see [20] for further details. The IGA and FEA as well as the elasto-plastic Drucker-Prager model discussed above have been implemented in our in-house Fortran code.
, see also Equation (15). For the numerical integration of the constitutive evolution equations we use a standard Euler backward scheme. The reader is referred to ( [20] , Sec. 7.2) which gives a detailed description of the numerical implementation procedure and also the format of the algorithmic tangent stiffness Dats. We like to mention that at the apex of the yield surface cone, the return vector is contained by a complementary cone, illustrated in Figure 7, see [20] for further details. The IGA and FEA as well as the elasto-plastic Drucker-Prager model discussed above have been implemented in our in-house Fortran code.
5. Numerical Studies
To validate the performance of isogeometric analysis for soil-plasticity, three numerical benchmark models have been established. The models have all been simulated for soils in saturated conditions using the Drucker-Prager criterion. The models evaluated consist of one two-dimensional model of a strip footing and two three-dimensional cylindrical soil profiles subjected to a prescribed force and prescribed displacement respectively.
5.1. Two-Dimensional Study
A two-dimensional model of a strip footing on sandy silt has been analyzed. Due to the symmetric properties of the problem the analysis contains only half of the footing. The geometry and boundary conditions are shown in Figure 8. To model the load from a flexible footing a vertical pressure of 180 kPa is applied in 50 equal steps.
The problem is solved for plane strain conditions using quadratic NURBS- based IGA and conventional FEA with 5 different meshes. In order to compare the two methods the element meshes have been constructed using quadratic isoparametric elements for both IGA and conventional FEA. The element size ranges from a coarse mesh with elements of 2 × 2 meters down to a mesh with elements of 0.25 × 0.25 meters. The mesh data and degrees of freedom for each mesh are shown in Table 1. The material parameters of the soil in the two dimensional model are shown in Table 2.
Figure 9 shows the ground surface displacements under the flexible footing. To make the comparison clearer, we compare the results at two points along the ground surface. The first point, A, is placed at the center of the footing and the second point, B, is placed at the edge of the footing, see also Figure 8. It can be seen that the displacements are in good agreement at center of the footing but
![]()
Figure 7. Illustration of return to the apex of the yield surface for the Drucker-Prager criterion.
![]()
Figure 8. Geometry and boundary conditions for the flexible footing model.
![]()
Table 1. Mesh data for the two-dimensional simulations.
![]()
Table 2. Material parameters for the soil.
![]()
Figure 9. Ground surface displacements underneath along the loading surface.
that there is a minor difference between the displacements from the isogeometric- and conventional finite element analysis at the edge of the footing (x = 2).
Figure 10 displays the load/displacement response in point A and B for the finest mesh. By studying the load/displacement response in Figure 10, the differences between the IGA and FEA results in point B become more apparent. The results for point B showed in Figure 10 are of special interest. The NURBS basis functions used in the isogeometric analysis provides continuous stress fields at the edge of the footing, where discontinuous stresses can be expected. The continuous stress will in turn affect the development of plastic strains at the edge of the footing.
The effects of the continuous stress fields that result from the NURBS basis functions can be seen in Figure 11, where the evolution of the plastic zone under the footing is displayed. From load steps 20 - 22 in Figure 11 it can be seen that the initial plastic strains are slightly different at the edge of the footing in the conventional finite element analysis compared to the isogeometric analysis. The difference in plastic strains at the edge of the footing corresponds to the diverging displacements seen in Figure 9 and Figure 10. For the isogeometric analysis the plastic strains originate under the center of the footing and reaches the edge of the footing during increased loading. In the finite element analysis, however, the plastic strain originates both under the center of the footing and at the edge of the footing simultaneously. Studying the displacements in point A and B for each element mesh, we compare the mesh size dependencies in Figure 12. The figure show the deviation of the displacement for each mesh compared to the
![]()
Figure 10. Load/displacement response at point A and B for the finest mesh (4800 elements).
![]()
Figure 11. Evolution of the effective plastic strains. The effective plastic strains from the inite element analysis and isogeometric analysis at six different load steps.
![]()
Figure 12. Comparison of the convergence of the displacement between FEA and IGA, for point A (a) and for point B (b).
results from the finest mesh used. The graphs show that the convergence for the isogeometric analysis and the conventional finite element analysis are comparable.
5.2. Three-Dimensional Studies
The two three-dimensional studies in this work are composed of a cylindrical soil profile with a 2:1 height/diameter proportion. In the first example, the cylindrical soil profile is subjected to a prescribed displacement at the top of the cylinder, in the second study the soil profile is subjected to a confining pressure and an increased vertical load at the top of the cylinder. The geometry and boundary conditions of the three-dimensional examples are presented in Figure 13. In both examples, a perfect elasto-plastic Drucker-Prager criterion, matched to the compressive meridian of the Mohr-Coulomb criterion has been used to model soil plasticity. The material properties for the soil in both studies are given in Table 3. For both IGA and conventional FEA 27 node isoparametric elements have been used to model the cylinder. The mesh data used are presented in Figure 14. Using NURBS parameterization an exact cylinder can be modeled. Whereas, for conventional FEA the geometry depends on the density of the mesh.
![]()
Table 3. Material parameters for the soil in three-dimensional studies.
![]()
Figure 13. Boundary conditions for the three-dimensional models. The displacement-con- trolled analysis is fixed in the bottom of the cylinder and has no horizontal constraints at the top (a). In the load controlled analysis the bottom of the cylinder is assumed to be fixed (b).
![]()
Figure 14. The left hand side shows a horizontal view of the finite element mesh and on the right hand side shows the conventional FEA (top) and IGA (bottom) meshes viewed from the top. The figure also includes mesh data used in the simulations.
5.2.1. Displacement Controlled Analysis
In the displacement controlled analysis a total strain of 7% is applied over 100 equal time by prescribing a displacement at the top surface. To compare the results from the isogeometric analysis with the finite element analysis, Figure 15 shows the applied pressure normalized to the cohesion against the axial strains.
To study the effects of the mesh density, Figure 16 shows the average vertical
![]()
Figure 15. Load/displacement response for the displacement controlled analysis of the cylindrical soil profile.
![]()
Figure 16. Deviation of the average displacements on the top surface of the sample.
stress components over the top surface of the soil profile for each mesh normalized to the vertical stress from the finest mesh. From Figure 16 it is clear that the deviation of the vertical stresses is slightly less pronounced in the results from the isogeometric analysis compared to the conventional finite element method. Comparing the results from the two dimensional example, the authors judge that the difference arises from the beneficial geometrical parameterization using NURBS in the isogeometric analysis.
5.2.2. Force Controlled Analysis
In the force-controlled example the soil profile is subjected to a confining pressure, σc, and an axial load, σv, acting on the top surface as illustrated in Figure 13(b). The analysis is run over 100 load steps. The load is applied by first increasing the confinement pressure to 3 kPa after which the vertical load is increased to 14 kPa. To compare the results from the isogeometric analysis to the results from the conventional finite element analysis, the applied force, normalized to the cohesion, is plotted against the axial strains in Figure 17. The results show that the solutions are in good agreement but that there is a difference between the displacements from the isogeometric analysis compared to the finite element results. Comparing the deviation of the displacement at the top surface for the load controlled example, the influence of using the exact geometry in the isogeometric analysis becomes more evident than for the displacement-controlled analysis, see Figure 18 and Figure 16. This would be expected as the confining pressure σc will be more accurate using a soil profile made out of a perfect cylinder, than one discretized with Lagrangian polynomials. This can be seen in Figure 18 where the results from the coarser meshes clearly are in error.
6. Summary and Conclusion
The aim of this work is to evaluate the isogeometric framework for numerical
![]()
Figure 17. Deviation of the average displacements on the top surface of the sample.
![]()
Figure 18. Deviation of the average displacements of the top surface of the cylinder.
analysis of soil behavior. To compare IGA to conventional FEA, the Drucker- Prager criterion has been implemented together with a NURBS-based isogeometric framework. A numerical study has been conducted using NURBS-based isogeometric analysis comparing the results with results from analysis performed using the finite element method. The numerical examples presented show, that for drained soils; the results from isogeometric analysis are overall in good agreement with the conventional finite element method in two- and three-dimensions. However, the results from the two-dimensional example presented illustrate that the higher continuity of the basis functions used in IGA can have an effect on the plastic strains where abrupt stress changes can be expected. For the three- dimensional examples presented in this paper the isogeometric analysis has performed as good as or better than the finite element method, comparing the load/displacement response. To compare the computational efficiency of IGA and conventional FEA is not within the scope of this study. Further, geotechnical applications like retaining walls in weak soil or installations of friction piles often involve complicated contact problems and fluid flow, hence could benefit from using the isogeometric framework.
Acknowledgements
The Development Fund of the Swedish Construction Industry, SBUF, supported this work. The support is gratefully acknowledged.