Effect of Parameters on Potential Induced Degradation of Solar Cell ()
1. Introduction
Nowadays, solar cells are widely used to generate electricity without any environmental disturbance such as thermal or atomic power generation of electricity [1] [2] . It is one of the ultimate solutions for the sustainable energy generation in order to save the earth from the global warming problem. Solar cells have been spreading rapidly in these days. Solar cells are used in a space craft where any energy is not provided other than sun light as well as on roofs of ordinary houses. Anyway the solar cells are installed in rigorous circumstances of outside, depending on the climate of the place to be installed.
Recently, it was recognized that solar cells are degraded slowly for years. This degradation attracted much attention after Swanson et al. reported that the degradation reached 30%. This is a big problem for the practical use. The degradation is now known as a potential induced degradation (PID) [3] [4] [5] . This physical principle of the degradation is not yet clarified well. So it is quite important to study PID for practical applications.
Our group assumes that PID is induced by a thunderstroke. In Japan, there are several thunderstrokes in a year. Since usually solar cells are exposed in the air, thunderstroke directly affects the solar cell system. In our previous paper, we reported the effect of lightning current on a solar cell by means of simulation [6] . It was clarified that the PID derived from the dielectric breakdown in the glass covered over the solar cell. And the existence of water on the glass plays a critical role to enhance the induced electric field in the glass to a great extent.
In this paper, we study the effects of four kinds of parameters on the induced electric field in the glass. They are the waveform, peak value, the front duration and the position of the lightning current because they are the basic parameters.
2. Theory
The well-known Maxwell’s electromagnetic equations are shown here.
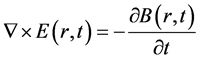
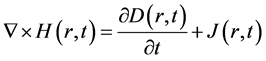
with the help of B = μH, D = εE and J = σE,
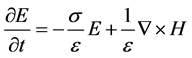
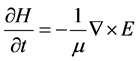
are obtained. These equations were transformed to difference equations. We applied the well-known Yee algorithm [7] in order to perform the numerical calculation. Actual calculation steps are shown in the literature. We used the differential-based absorbing boundary condition proposed by Mur [8] .
All the spatial finite differences Δx, Δy and Δz should be under the tenth of the wave length. As for the time finite difference Δt, it should be consistent with the Courant condition that is
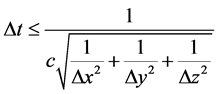
The readers should refer to the literature [3] for more information.
3. Modelling
The solar cell panel treated here is described. Figure 1 shows the top and bottom view of the panel in (a) and a sectional view in (b). The panel consists of three layers of a glass plate, a solar cell and EVA for encapsulation, and back-sheet (PET) from the surface to the bottom. The panel was fixed by an aluminum frame around it. The solar cell itself was treated as a perfect conductor here. It is assumed that water exists on the glass to simulate a rainy weather. The water plays a critical role for dielectric breakdown [3] .
The analytical model of the solar cell panel is shown in Figure 2. The aluminum frame was earthed through 10 Ω at the four corners. The two output terminals were shunted and then earthed through 500 kΩ. The earth is expressed as a perfect conductor with the thickness of 0.01 m. The electromagnetic parameters such as relative dielectric constant, relative permeability, and electric conductivity for each material are shown in Table 1.
We describe here the model of lightning current where only the indirect thunder stroke was considered. The lightning current was located at the point P in Figure 2 and flowed along the z axis. The parameter LX and LY was taken to be the same. The waveform of the lightning current was chosen from the two kinds: impulse or step waveforms. The current was uniform along the z axis.
![]()
Figure 1. The schematic diagram of the top and bottom view (a) and the sectional view (b) of the solar cell panel. The unit in the figure is mm.
![]()
Figure 2. The analytical model of the solar cell panel. The I at P in the left side indicates the thunderstroke current to flow along the z axis.
![]()
Table 1. The parameters set used in our simulation
![]()
Figure 3. The voltages of V1, V2, and V3 is defined in the figure.
![]()
Figure 4. The lightning current of the two types are shown. I1 and I2 have the step like and impulse waveform, respectively. The form of front duration is the same that endures 0.1 μs.
![]()
Figure 5. The induced voltage V1 in the vicinity of an aluminum frame. The wave form of the lightning current was taken to be two types.
Analytical space was in the area of 1.6 m × 1.6 m × 0.4 m. The differences of Δx, Δy and Δz are 10 mm, 10 mm, and 1 mm, respectively. In order to satisfy the Courant condition, the time difference was set to 1 ps. We took the 300,000 time steps that are far larger than the head voltage width.
We assume the voltages V1, V2, and V3 as shown in Figure 3. Among the three voltages, V1 is the most critical one [3] and only this voltage is calculated in this paper. And the V1 was calculated in the vicinity of an aluminum frame [3] .
4. Results and Discussion
We first consider the waveform of lightning current. Figure 4 shows the two kinds of them. I1 has a step waveform while I2 has an impulse one. The maximum value was 20 kA in common. For the impulse waveform, the front duration of the current was was 0.1 μs and the time to half value of the current was 1 μs. Both of LX and LY were 0.3 m.
Figure 5 shows the induced voltage of V1 in the vicinity of an aluminum frame. The blue and the sky blue lines represent the step like and the impulse current responses, respectively. The maximum spikes in both cases are very similar that surpass 20 kV. From this fact, the height of the spike should be determined by the very head part of the lightning current within 0.1 μs. So the difference between I1 and I2 do not affect the induced voltage. It suggests that the step like current is valid for the numerical simulation for this kind of analysis.
Next we discuss the dependence of the height of the lightning current with a step like form. Both of LX and LY were 0.3 m, and the front duration of the current was 0.1 μs. The peak heights of the current were chosen to be 20, 50, 70, and 100 kA. The simulation results are shown in Figure 6. The voltage was also V1 in the vicinity of an aluminum frame. The maximum spike was respectively about 21, 50, 60, and 85 kV. The maximum spike rises monotonically with the current, almost linearly.
The difference in the front duration is discussed here. The results for the four front durations of 0.1, 0.3, 1, and 8 μs are shown in Figure 7 where both of LX and LY were 0.3 m, and the height of the current was 20 kA. The induced voltage
![]()
Figure 6. The induced voltage V1 in the vicinity of an aluminum frame. The height of the lightning current was varied.
![]()
Figure 7. The induced voltage V1 in the vicinity of an aluminum frame. The length of the front duration of the step like lightning current was varied.
![]()
Figure 8. The induced voltage V1 in the vicinity of an aluminum frame. The position (LX and LY) of the lightning current was varied.
V1 was calculated in the vicinity of the aluminum frame. As the front duration becomes the longer, the peak maximum of the spike in the induced voltage reduces. Also it is recognized that the high frequency component is less dominant when the duration is large. But the lightning current is a natural phenomenon, and then it may be quite difficult to control the current anyway. If possible, the current should be varied slowly to protect from the dielectric breakdown.
Finally we see the dependence of the position of the lightning current. The step like current was characterized with the maximum value of 20 kA and the front duration of 0.1 μs. The position of LX and LY were simultaneously varied 0.2, 0.3, 0.4, and 0.5 m. The induced voltage V1 was also calculated in the vicinity of the aluminum frame. The results are shown in Figure 8. As the distance becomes large, the maximum peak of the spike voltage is gradually lowered. The dimension of the panel was 0.5 m, the effect of the variation of position is not so formidable.
LX and LY ranges from 0.2 to 0.5 m where the dimension of solar cell was 0.5 m. These are the same order of magnitude. In this range, no significant difference in the effect was observed. But the peak maximum of the induced voltage was slightly greater when the position of the lightning current was nearer to the solar cell.
5. Conclusion
We performed the numerical calculation of the induced voltage across the glass covering the solar cell unit in the case that thunderstroke hit near the solar cell panel. The calculation was based on the fundamental Maxwell’s electromagnetic equations. The parameters of the wave form, the peak value, the front duration and the position of the lightning current were varied and the peak maximum of the induced voltage was examined. Our results showed that the prominent difference was not seen if the lightning current had an impulse or a step like form. The peak maximum of the voltage depended mainly on the front duration of the current. The current magnitude linearly affected the peak maximum of the voltage. The position that ranged in the same order of the dimension of the solar cell panel, the triggered effect was not so noticeable.