1. Introduction
MIMO technology has been attractive in wireless communications [1] [2], compared with conventional communication systems, which are called Single-Input Single-Output (SISO) systems, the use of multiple antennas provides means for simultaneous transmissions and spatial redundancy to the transmitted signals that helps to improve the throughput performance of MIMO over SISO [3].
2. Decomposition of CPM
The transmitted baseband CPM signal is expressed as
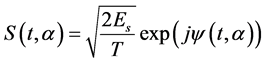(1)
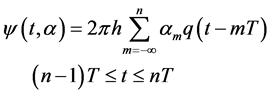(2)
where 
denotes the symbol period,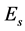 
is the transmitted energy per symbol and 
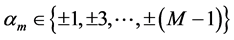denotes actually the transmitted symbol at the mth signal period, 
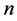is data length, 
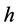is the modulation index, 
, 
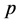and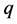 
are relatively prime. 
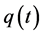is
(3)
where we assumed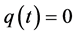 
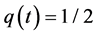for
, 
for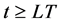 
and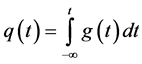
. Then (2) can be written as
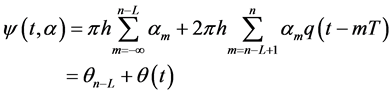(4)
The CPM modulation is said to be full- response if ![]()
and of partial response if![]()
. Given as![]()
, ![]()
after simplifying and modulus ![]()
operation,
![]()
(5)
where![]()
, ![]()
is irrelevant item. Then (1) can be written
![]()
(6)
It can be seen that CPM signals can be determined by the current input ![]()
and previous ![]()
input ![]()
as well as their accumulation
![]()
completely, so any CPM scheme can be divided into a
continuous phase encoder (CPE) and a memoryless modulator (MM) [11].
3. System Model
We consider a generic transmitter block diagram of MIMO system is shown in Figure 1 with two transmitting antennas. The space-time coding process multiplexes the coded data stream into two parallel sub-streams. And then each stream coded using LDPC code, the interleaving is next step. Finally, the space-time bits are mapped into CPM symbols. It should be note that the modulated signal cannot be interleaved because interleaving destroys the continuous phase property of the modulated signal. The symbols transmitted per frame can be represented by a matrix ![]()
and the element ![]()
is the transmitting symbol on the antenna ![]()
during the symbol period![]()
.
The channel is assumed to be invariant within a frame and change independently from frame to frame, and ideal power control is considered here result in the received signal power is equal for all antennas. Thus the received symbols during a frame can be written as
![]()
(7)
where channel matrix ![]()
is composed by independent and identically distributed Rayleigh fading coefficients, its elements ![]()
denote the fading factors of the sub-channels, ![]()
is the zero-mean complex Gaussian noise.
4. Iterative Detection and Decoding
The joint iterative CPM decoding and LDPC decoding algorithm can improve
the BER performance through exchange the soft information. We apply this algorithm to the MIMO system and get a scheme which is shown in Figure 2. It can be seen that the receiver includes two iterative processes: the inner loop is responsible for the demodulation and decoding, outer loop provides a better estimation of transmitted signal for the interference canceller in each a iteration.
MIMO detector uses a Minimum Mean Square Error (MMSE) detection technique, so the problem is to determine weighting matrix ![]()
in order to minimize![]()
, we have
![]()
(8)
In other words, the function of the ![]()
is to reverse channel, assume that ![]()
is the estimation of ![]()
and write
![]()
(9)
where![]()
. Based on singular value decomposition (SVD) of the type, the noise power through detector written as
![]()
(10)
According to the
![]()
and times a unitary matrix will not change vector norm![]()
, after a series of transformation, the expectations of Equation (10) is![]()
(11)At this point, the output of MMSE detector can be equivalent to each CPM signals from transmitting antennas through the white Gaussian noise channel
which have increased the noise gain than before. We use the matched filter group to obtain the code word information probabilities ![]()
for inner loop which is shown in Figure 3.
Contain LDPC code, interweaver and CPE as this inner loop, which CPM- SISO makes use of Log-MAP algorithm and LDPC-SISO adopts Log-FFT-BP iterative decoding algorithm. ![]()
and ![]()
respectively denote code word and the information probability sequence of input for CPM-SISO, ![]()
and ![]()
as output probability sequence. In the same way, ![]()
and ![]()
denote code word and the information probability sequence of input for LDPC-SISO, ![]()
and ![]()
as output probability sequence. The probability of the sequence ![]()
from sub-system CPM-SISO, after de-interweaving, is fed to the LDPC-SISO decoder as input information probability![]()
, then ![]()
from sub-system LDPC-SISO after de-interweaving, obtain information probability to input CPM-SISO. After some iteration of inner make loop hard decision according to the last iteration of![]()
.
For the last iteration ![]()
of CPM-SISO, make a hard decision and no de-interweaving to secondary modulation, feedback secondary modulation signal to the interference canceller. In the next iteration of the outer loop, interference canceller provides the better input for inner loop.
5. Simulation Results
According to the previous sections, we have established a MMO system model at Rayleigh flat fading channel and assumed that perfectly known at the receiver. The length of each unencoded substream is equal to LDPC information bits, interweavers are chosen randomly. The other parameters are illustrated in figures below.
Figure 4 show that the system channel capacity increase with the number of antenna linearly, this paper takes the scenario which sending antenna is equal to receiving. In Figure 5 we compare the performance of the system for different numbers of receiving and transmitting antennas number. Where LDPC code length is 1536 bits, rate 1/2, CPM Signal form is OM2RC. We see that the performance of the system improved by increasing the number of transmitting and receiving antennas in the background of low SNR. From the two figures, we can give attention to both high-speed transmission and reliable transmission.
Figure 6 shows the BER trend along with the change of LDPC length when
![]()
Figure 3. Block diagram of the iterative decoder.
![]()
Figure 4. The channel capacity with different number of antenna.
![]()
Figure 5. BER with different number of antenna.
2 * 2 MIMO system easy to extend to more antennas. LDPC rate are employed 1/2. Modulation method is same as above OM2RC. As it may be seen, with the increase of code length, BER performance of the system is gradually improved. Therefore, the longer the LDPC code length, the better the performance of the system.
With the method of iterative decoding to optimize system performance, the performance impact of iteration times and must be considered. Figure 7 for the number of iteration affect the performance of the system. In simulation, 2*2 MIMO system with LDPC information bits is 512 bits, rate 1/2, the interior of
![]()
Figure 6. Performance of system with different LDPC length when 2*2.
![]()
Figure 7. Performance of the system at different iteration times.
the LDPC code iteration for 5 times. The same goes for CPM. It can be seen that with the increase of the number of iterations, and decrease of the system BER curve tends to convergence, and with the increase of signal-to-noise ratio, number of iterations the impact on the BER is more and more obvious.
6. Conclusion
In this paper, we analyze and derive the decomposition of CPM modulation signal, and applied a joint coded modulation with LDPC to MIMO architecture. Through simple MMSE-based detection and low-complexity iterative decoding with cancellation, both BER and channel capacity of improvements are achieved. We compared the effect of the number of antenna, code length and iteration times on the combined code modulation in the 2 * 2 MIMO system emphatically. The result shows that: The system has better performance for different code length and iteration times than SISO, which meets the requirements for real- time communication channel. At last, this algorithm is complete by software, so it costs lower equipment, and can be simple and practical.
Acknowledgements
This paper is funded by the International Exchange Program of Harbin Engineering University for Innovation-oriented Talents Cultivation, the Open Research Fund of State Key Laboratory of Tianjin Key Laboratory of Intelligent Information Processing in Remote Sensing (Grant No. 2016-ZW-KFJJ-01), the National Natural Science Foundation of China (Grant No. 61403093), the Assisted Project by Heilongjiang Province of China Postdoctoral Funds for Scientific Research Initiation (Grant No. LBH-Q14048), and the Fundamental Research Funds for the Central Universities (Grant No. HEUCF160813).