1. Introduction
Adaptive frequency hopping is the core technology in modern military ultra- short electric wave communication. Channel quality evaluation is the core of adaptive frequency hopping system. According to the signal received from hopping channels, we can use the real-time channel quality judgment rules to analyze the quality of the channel, then we can determine whether the jump frequency is interfering the normal communication [1]. At last, we can provide evidence for control of hopping adaptive to conduct normal communication. The communication channel quality assessment is generally based on the bit error rate (BER), frame error rate (FER), received signal strength (RSS), signal to noise ratio (SNR) or other parameters of each channel to achieve the estimation. Frequency hopping communication systems generally use two kinds of method: one is based on BER and the other is based on SNR. The channel quality assessment method based on BER calculation estimates error rate by comparing the estimated value of the detection with the threshold after detecting and satisfying error coding, the channel which is greater than the threshold is determined to be a bad channel, which is less than the threshold determined to be a good channel. However, with the hopping rate is greater than the information rate in military field in general, the calculation of the error rate of a channel is extremely difficult, so we can’t use the channel quality evaluation method based on BER. SNR is also an important indicator to measure the quality of communication, so it can be used as a valid basis for adaptive control.
CPM is a constant envelope modulation since the phase changes continuously, and it overcomes the phase mutation occurred when symbols convert mutually. At the same time, the waveform has good roll-off characteristics. Because of its characteristics of continuous phase, we can use the similar characteristics of CPM carrier phase with MPSK at the final value 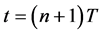 which is based on the phase obtained after sampling time [2]. On this basis, we come up with a channel estimation processing method which simplifies the algorithm computation of traditional SNR estimation and gets good performance. Meanwhile, to improve error performance and bandwidth efficiency, we use LDPC coded CPM scheme. The rest of the paper is organized as follows. Section 2 introduces the traditional methods of SNR estimation. Section 3 introduces the SNR estimation method for CPM. Simulations are discussed in Section 4. Finally, we conclude the paper in Section 5.
which is based on the phase obtained after sampling time [2]. On this basis, we come up with a channel estimation processing method which simplifies the algorithm computation of traditional SNR estimation and gets good performance. Meanwhile, to improve error performance and bandwidth efficiency, we use LDPC coded CPM scheme. The rest of the paper is organized as follows. Section 2 introduces the traditional methods of SNR estimation. Section 3 introduces the SNR estimation method for CPM. Simulations are discussed in Section 4. Finally, we conclude the paper in Section 5.
2. The Traditional Methods of SNR Estimation
Now there are many ways of achieving wireless communication in signal to noise ratio estimation. Generally hopping systems adopt the following three classical algorithms to estimate SNR depending on their conditions: high-order cumulates estimator, data fitting estimator and eigenvalue decomposition of signal auto-correlation matrix estimator [3]. Ref. [4] analyses and compares several classic SNR estimation algorithms in the additive white Gaussian noise (AWGN) channel. In all the methods of SNR estimation algorithms, second and fourth moment estimation (M2M4) and maximum likelihood estimation (ML) method must keep being synchronized both in the carrier and clock; the Ref. [5] uses the training sequence configured to receive a signal from the correlation matrix to estimate the signal to interference ratio of time division multiple access (TDMA) system which is based on the signal space projection method; the Ref. [6] uses a signal fourth moment to estimate the constant envelope SNR; the Ref. [7] estimates the binding characteristics of the signal envelope of the non-con- stant envelope signals (MPSK, MQAM) by analysing the spectrum.
3. SNR Estimation Method for CPM
CPM is a constant envelope modulation, defined as
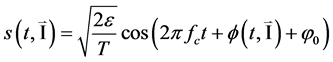 (1)
(1)
where 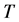 is symbol interval,
is symbol interval,  is symbol energy,
is symbol energy, 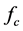 is the carrier frequency,
is the carrier frequency, 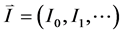 is M-array data sequence transmitted.
is M-array data sequence transmitted. 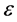 is the energy per channel symbol and
is the energy per channel symbol and 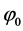 is the initial carrier phase.
is the initial carrier phase.
The carrier phase of continuous phase modulation is
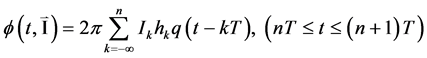 (2)
(2)
where  is the M-array information symbol sequence selected from
is the M-array information symbol sequence selected from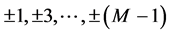 ,
, 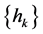 is the modulation index series. The modulation index is limited to take the same situation as discussed in this paper.
is the modulation index series. The modulation index is limited to take the same situation as discussed in this paper. 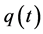 is a continuous and monotonically increasing function.
is a continuous and monotonically increasing function.
The trajectory of the CPM phase can be represented as a tree phase. Using a tree to represent the phase trajectories can truly reflect from one state to another when the phase changes. The phase of CPM can also be used as a simple method of representation. For example, only considered to getting phase within the symbol duration time, the phase of CPM is changed. It can’t reflect the phase change between adjacent states truly, but we can simplify the analysis phase. Now we can derive the carrier phase in the case of the final value of time when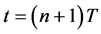 . For all-response
. For all-response 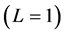 and partial response
and partial response 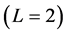 LRC pulse, the integration waveform
LRC pulse, the integration waveform  in the final value
in the final value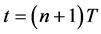 . Substituting
. Substituting ![]() into the Equation (3) as
into the Equation (3) as
![]() (3)
(3)
If we use REC pulse for CPM, the integration waveform ![]() of the final value of the corresponding phase time
of the final value of the corresponding phase time ![]() is
is
![]() (4)
(4)
For complete response LRC pulse C PM signal satisfy the above derivation of integral waveform ![]() not only in the time of
not only in the time of ![]() but also in a
but also in a
non-final value time![]() .
.
The following discussion is limited to take the same modulation index h. The carrier phase of the CPM in final time is selected as![]() .
.
![]() (5)
(5)
So we can see that in the final phase time![]() , the CPM signal changes from one state to another, and then the carrier phase changes by
, the CPM signal changes from one state to another, and then the carrier phase changes by![]() . When L = 1,
. When L = 1, ![]() , on the signal vector, carrier phase of CPM is 0,
, on the signal vector, carrier phase of CPM is 0, ![]() ,
, ![]() ,
, ![]() (or
(or ![]()
![]()
![]() ,
,![]() ), it is same with the carrier phase of 4PSK. When
), it is same with the carrier phase of 4PSK. When ![]()
![]() ,
, ![]() , on the signal vector, the carrier phase of CPM is same with the carrier phase of 8PSK. We assume that the system in line with the conditions of additive white Gaussian noise, the CPM signal in the value of phase final
, on the signal vector, the carrier phase of CPM is same with the carrier phase of 8PSK. We assume that the system in line with the conditions of additive white Gaussian noise, the CPM signal in the value of phase final ![]() after sampling time is
after sampling time is
![]() (6)
(6)
where ![]() is the real signals;
is the real signals; ![]() is the amplitude value;
is the amplitude value; ![]() is the coordinates of the points on constellation;
is the coordinates of the points on constellation; ![]() is zero mean of complex Gaussian white noise, the variance is
is zero mean of complex Gaussian white noise, the variance is![]() .
.
Hypothesis ![]()
![]() (7)
(7)
We generally assumed that the transmission signal of each sequence is identically distributed and mutually independent, then we can get
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
Fourth-order copulation of complex Gaussian noise is identically zero, and it is independent of each other between signal and noise. So we can get the following formulas from above formulas and assumptions as
![]() (12)
(12)
where![]() ,
, ![]() ,
, ![]() represent received signal, the transmission signal and noise respectively. The variance of representative received signal, the transmission signal and noise are
represent received signal, the transmission signal and noise respectively. The variance of representative received signal, the transmission signal and noise are![]() ,
, ![]() ,
,![]() .
.
This SNR estimation algorithm flow is as follows:
1) Use the received signal sample sequence![]() ,
, ![]() to calculate the cumulative estimated value
to calculate the cumulative estimated value ![]() and the variance estimates
and the variance estimates![]() ;
;
2) Calculated variance estimates of noise component![]() ;
;
3) Estimated energy of the transmitted signals![]() ;
;
4) According to the formulas above to calculate the estimated value of SNR:
![]() (13)
(13)
We judge the channel quality by the results of SNR estimation, and detect the frequency which is interfered and use a better quality of different frequencies to replace interfered frequency points respectively to achieve adaptive frequency hopping [8]. It is an adaptive algorithm based on analysis of higher moments estimation method, as it is based on the second order and fourth order to estimate the received signal, so it is no need to recovery phase. As a cumulative amount algorithm, it does not require a receiver judgment. And it is also a Non-Data- Aided estimate [9].
4. Simulations and Analysis
4.1. The Affection of Signal Length
When M = 8 in CPM signal, the information block length N uses the value as 80, 160, 320 respectively, to get the mean and NMSE values of SNR estimate between 0 - 20 dB. We can see from Figure 1 and Figure 2, with the N increasing, the estimated value of the NMSE decreasing, the relations between the length of the symbol and the estimation error is inversely proportional. In practice, we need to select the appropriate length of N under the requirements of the observed data based on the estimated error. On the other hand, when N is given, the estimated variance is of low SNR, noise ratio estimation bias and variance is larger; With the N increasing in SNR, it estimates closer to the true value, and it has a smaller estimate of standard deviation. In practice, our algorithm can achieve very good estimation performance when the communication signal to noise ratio is generally in the range of 4 - 20 dB.
4.2. The Universality for Different M
When information block length N is 320 for CPM signal, M uses the value as 2, 4, 8 respectively, h = 1/4, to get the mean and standard deviation values of SNR estimate between 0 - 20 dB. Figure 3 and Figure 4 show that different estimates
![]()
Figure 1. The mean of SNR estimate with different N.
![]()
Figure 2. The NMSE of SNR estimate with different N.
of the modulation are almost consistent. Description of the algorithm for different decimal M for CPM modulation is insensitive, therefore, the algorithm is apply for different M.
4.3. Reduce Complexity of Operation
Higher order statistical moments algorithm uses the relationship between the higher-order statistical moments to estimate the SNR. It uses the second moment and fourth moment in computation. The classic blind channel estimation methods are based on the data received from the correlation matrix (or cross- correlation matrix), such as subspace method (SS), Minimum Noise Subspace (MNS), using Singular Value Decomposition (SVD) or Eigenvaue Decomposition
![]()
Figure 3. The mean of SNR estimate with different M.
![]()
Figure 4. The NMSE of SNR estimate with different M.
(EVD) to achieve blind channel estimation method. The calculation complexity of SVD is![]() , where
, where ![]() is the rank of autocorrelation matrix. The calculation complexity of higher order statistical moments algorithm is
is the rank of autocorrelation matrix. The calculation complexity of higher order statistical moments algorithm is![]() , whose complexity is reduced greatly.
, whose complexity is reduced greatly.
5. Conclusion
By analyze and derive the phase of CPM modulation signal, we find that the phase of CPM signal after sampling in the final time ![]() has the similar characteristic with MPSK signal, so we use an effective method to estimate the channel and simulation. The result shows that the algorithm has better estimation accuracy and stability for different M of CPM signal. Meanwhile, with the N increasing in SNR, it estimates closer to the true value, and it has a smaller estimate of standard deviation. So the algorithm can meet the requirements for the real-time communication channel. At the same time, LDPC coded CPM can improve power efficiency and attain high error correcting capacity [10]. At last, this algorithm is realized by software completely. Therefore it can reduce the hardware costs and complexity largely.
has the similar characteristic with MPSK signal, so we use an effective method to estimate the channel and simulation. The result shows that the algorithm has better estimation accuracy and stability for different M of CPM signal. Meanwhile, with the N increasing in SNR, it estimates closer to the true value, and it has a smaller estimate of standard deviation. So the algorithm can meet the requirements for the real-time communication channel. At the same time, LDPC coded CPM can improve power efficiency and attain high error correcting capacity [10]. At last, this algorithm is realized by software completely. Therefore it can reduce the hardware costs and complexity largely.
Acknowledgements
This paper is funded by the International Exchange Program of Harbin Engineering University for Innovation-oriented Talents Cultivation, the Open Research Fund of State Key Laboratory of Tianjin Key Laboratory of Intelligent Information Processing in Remote Sensing (Grant No. 2016-ZW-KFJJ-01), the National Natural Science Foundation of China (Grant No. 61403093), the Assisted Project by Heilongjiang Province of China Postdoctoral Funds for Scientific Research Initiation (Grant No. LBH-Q14048), and the Fundamental Research Funds for the Central Universities (Grant No. HEUCF160813).