Understanding the Competitive and Cooperative Interactions between Probiotics and Autochthonous Intestinal Bacteria

Tyler Brown¹, Majid Bani-Yaghoub², Jose F. García-Mazcorro³

¹Department of Biological Engineering, University of Missouri-Columbia, Columbia, Missouri, USA.
²Department of Mathematics and Statistics, University of Missouri-Kansas City, Kansas City, Missouri, USA.
³Facultad de Medicina Veterinaria y Zootecnia, Universidad Autónoma de Nuevo León, General Escobedo, Nuevo León, México.

DOI: 10.4236/jbm.2017.54007                

Abstract

The present study combines the theory and the experimental data to predict the changes on intestinal bacterial populations during ingestion of beneficial probiotic bacteria. Our proposed model is a modified version of the Lotka-Volterra model, which takes the probiotic administration into account. Using the linear stability analysis of the model, the conditions for coexistence of the probiotics with other bacteria are established. Using the model fitted to the data of C. coccoides species and Bifidobacterium species, the effects of oral probiotics on autochthonous bacterial cultures is investigated. The estimated parameter values suggest that C. coccoides and Bifidobacterium facilitate each other during the probiotics administration, whereas they compete in the absence of the probiotics administration. This may suggest the beneficial effect of probiotic administration as it promotes the growth of C. coccoides species. The results also confirm prior studies showing that once probiotic supplementation is discontinued, the probiotic population and the promoting effect within the digestive tract will diminish.

Keywords

Bifidobacterium, C. coccoides, Lotka-Volterra Model, Probiotics, Stability Analysis

1. Introduction

Probiotics are live microorganisms which are thought to confer a health benefit on the host, when administered in adequate amounts [1] . For several decades, probiotic bacteria have been studied for their potential beneficial effects upon their host organism [2] [3] [4] . Probiotics are believed to affect the abundance of autochthonous intestinal bacteria by competing with pathogenic bacteria for host binding sites [5] . By reducing the permeability of the intestinal wall, probiotics may protect against the invasion of other bacteria [5] . Other studies have shown that probiotics can reduce the frequency of respiratory infections [6] , prevent a high number of antibiotic-associated diarrhea cases [7] , help maintain remission of inflammatory bowel diseases [5] , may reduce the occurrence of diarrhea and yeast infections in AIDS patients [8] , and significantly reduces high cholesterol levels [9] . Other benefits of probiotics include fewer infections, fewer antibiotics prescribed, and shorter hospital stay [10] .

Given the benefits and harms of probiotics, there is a strong need to unpack the underlying mechanisms governing the interactions between probiotics and intestinal bacteria. Using a mathematical modeling approach, the main objective of the present work is to investigate the effects of probiotics administration on the microbial ecology of the intestine. To achieve this goal, we focus on a group of probiotics with the genus Bifidobacterium. Previous studies suggest that certain dosage of Bifidobacterium may positively influence human health [14] [15] . In particular, while researchers found that a dose of 10⁸ live Bifidobacterium cells helped alleviate many symptoms associated with Irritable Bowel Syndrome, the same team found that 10⁶ live cells and 10¹⁰ live cells actually exacerbated the same symptoms [15] . Additionally, a study on severe acute pancreatitis patients found that adding 10¹⁰ probiotics (the mixture included but was not limited to Bifidobacterium) to the diet of these patients actually increased their mortality rate [11] . Thus, the effect of supplemental Bifidobacterium upon the host is potentially determined by dose size, but currently there is no clear explanation of why this is.

Patients with Irritable Bowel Syndrome and patients with Infectious Colitis exhibit very similar deviations from gut bacteria homeostasis when compared with healthy patients. Both Clostridium coccoides and Bifidobacterium populations are suppressed in the afflicted patients when compared with healthy subjects [16] [17] . Moreover, the balance between C. coccoides and members of the order Bacteroidales has been observed to be quite different in obese animals when compared with average healthy animals [18] . With this in mind, there seems to be a need to understand the relationship between Bifidobacterium and C. coccoides populations. For, if they compete against one another strongly, then perhaps the ingested Bifidobacterium can overpower the C. coccoides and produce some sort of deleterious effect. Conversely, if they facilitate one another’s populations, then Bifidobacterium supplementation can be seen as likely positive for the maintenance of the C. coccoides intestinal population.

Using a mathematical modeling approach and the collected data, this paper investigates the potential interactions between the Bifidobacterium and C. coccoides species, and we posit that such interactions exist because several studies suggest that bacteria populations within the intestines interact with each other [19] [20] . The goal of probiotic therapy should be to bring bacteria populations back to a homeostatic level [21] , so it is important to know how Bifidobacterium effects C. coccoides. Therefore the practical significance of this study is that mathematical models may ultimately reveal and quantify the possible interrelationships between the intestinal bacterial groups.

In the present work, C. coccoides species was selected because several studies have also used the Erec482, C. coccoides group, in human and animal studies [22] [23] [24] [25] . Also, this group is related to health in dogs [26] and showed high abundance and stability among individual healthy dogs in a paper from our research group [27] , thus making this group a good candidate to be found and quantified.

The rest of this paper is organized as follows. Section 2 provides details of data collection, model construction, model fitting, and analysis of the model. Section 3 provides the main finding of the present work including the possible outcomes of the model and prediction of the interactions between the species both in the presence and absence of probiotics administration. Section 4 provides a discussion of the results and delivers the main conclusions of this study.

2. Method

2.1. Overview

The present study combines the theory and the experimental data to predict the changes on intestinal bacterial populations during ingestion of beneficial probiotic bacteria. The temporal data of C. coccoides and Bifidobacterium species are collected before, during, and after probiotic (i.e., Bifidobacterium species) administration. Using a Lotka-Volterra Modeling approach, a mathematical model of probiotics and intestinal bacteria is constructed. The model is analyzed to determine the conditions for existence and stability of equilibria. The model is also fitted to data to determine the interaction between the species and to provide quantitative estimates of intestinal bacteria in response to probiotic administration.

2.2. Data Collection

A healthy Schnauzer adult dog received 2 tablets (2 times 10⁸ cfu (numbers of bacteria) of Bifidobacterium species) of Prostora® daily for a total of 4 days. During the 10 days of this study, the dog defecated approximately 30 grams of feces per day (~15 grams in the morning and ~15 grams at night). Fecal samples were collected before probiotic administration (Days 0, 1, and 2), during probiotic administration (Days 3, 4, 5, and 6) and after probiotic administration (Days 7, 8, and 9). Total fecal bacteria and two different fecal bacterial groups (i.e., the C. coccoides group and the probiotic group) were quantified in feces using fluorescent in situ hybridization. This technique relies on the bounding of fluorescently-labeled oligonucleotides probes to specific RNA sequences of the bacterial ribosomal RNA. This bounding allows the visualization and quantification of microorganisms by means of fluorescent detection. Figure 1 shows the estimated total number of C. coccoides group, the Bifidobacterium species and all other species. Moreover, Figure 2 shows the average amount of fecal Bifidobacterium and C. coccoides before, during, and after probiotic administration. Note that, high-throughput sequencing is another widely used method to determine the majority of all microbial groups but this technique relies on PCR amplification of genes (i.e. 16SrRNA gene) that have different copy numbers within each genome [28] and possess considerable intra-genomic variation [29] . Therefore, not even high-throughput sequencing can detect all bacteria. In fact, FISH is superior compared to sequencing in terms of true quantification of bacteria.

2.3. The Mathematical Model

Previous mathematical models for probiotic (in this case, Bifidobacterium and Lactobacillus) intervention have found it necessary to include parameters which

Figure 1. Estimated number of fecal bacteria before (days 0 - 2), during (days 3 - 6), and after (days 7 - 9) probiotic administration.

Figure 2. Average amount of fecal Probiotics (i.e., Bifidobacterium) and C. coccoides before, during, and after probiotic administration.

express the potential negative effects of probiotics upon the host organism by a degradation of the integrity of the intestinal wall [5] [30] [31] [32] [33] . Consequently, our model followed a similar approach using a Lotka-Volterra modeling approach. Specifically, the mathematical model (a set of ordinary differential equations) allows for cooperative or competitive interactions between the species, and it was employed to simulate the temporal variations of microbial flora due to administration of probiotics. The Lotka-Volterra models have proven to be useful when attempting to unpack the interactions within and between species in various ecological systems (see for example, [34] ). When we assume that dynamics of intestinal bacteria can be expressed by a Lotka-Volterra model of three bacterial groups, then the set of ordinary differential equations is given by:

Before and after During

probiotic administration probiotic administration

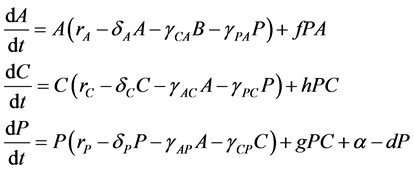(1)

where the population growth of species i, carrying capacity of species i and interactions between the species i and j are denoted by 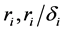and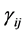, respectively. Parameters f, h and g relate to the possible interactions between the species during the probiotics administrations. Parameters 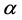and 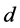are the entry and consumption rates of the probiotics during the administration, respectively. Figure 3 is a compartmental diagram representing the mathematical model. Moreover, Table 1 provides a summary of the model variables and the parameters.

2.4. Model Fitting and Stability Analysis

Using direct calculations and a geometric argument, the equilibrium solutions of model (1) were determined both in the presence and absence of probiotics administration. By linearizing model (1) about each equilibrium, the conditions for stability of each equilibrium were determined. The stability of the coexistence equilibrium was numerically verified for different sets of parameter values. Finally, using the Matlab optimization toolbox (the function fminsearch. m), mo- del (1) was fitted to the data and the specific parameter values were determined.

3. Results

3.1. Existence and Stability of Equilibria

Since variables A(t), C(t), and P(t) are bacterial population, we have

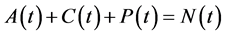, for all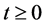, where N(t) >0 is total bacterial population at time t. By focusing on the last two equations of model (1) and substituting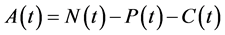. The model can be rewritten as:

Figure 3. A compartmental diagram representing the model of oral probiotic and intes- tinal bacterial groups A, C and P.

Table 1. Summary of the variables and parameters of the mathematical model.

Note: The parameters indicated in the last two rows are experimental parameters, which are set to zero before and after administration

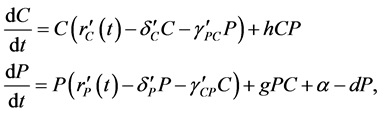(2)

where

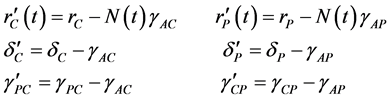(3)

Suppose that can be rewritten

(4)

where 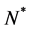is a positive constant and.

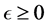In an unrealistic case, we may consider. Then, as shown in Appendix A, model (2) has up to four equilibria for the cases of before and after probiotics administration (i.e. when). These equilibria are the Extinc-

tion, Probiotics-free, C. coccoides-free

, and the Coexistence equilibrium. Details of the li-

near stability analysis of these equilibria is given in Appendix A. Table 2 is a summary of the model outcomes and the conditions for stability and existence of the equilibria.

As shown in Appendix B, for, model (2) has up to three equilibria for the case of probiotics administration (i.e. when and g are nonzero). These equilibria are the C. coccoides-free equilibrium and the Co- existence equilibria and. Details of the linear stability analysis of these equilibria is given in Appendix B. Table 3 is a summary of model outcomes and the conditions for stability and existence of the equilibria.

When, the number of equilibria is increased and the local stability of the above-mentioned equilibria may change. For small values of, the local stability of the above-mentioned equilibria (i.e.,) remains the same. This can be verified using perturbation methods. Also the following theorems are used to further investigate the stability of equilibria.

Theorem 1. Consider the system, continuous for

Table 2. Possible outcomes of Model (2) for and in the absence of probiotic administration.

Notes: ⁽¹⁾the symbol ~ indicates that one of the following conditions must be violated; ⁽²⁾depending on the initial conditions, the solution may converge to either equilibrium

Table 3. Possible outcomes of Model (2) for and in the presence of probiotic administration.

Note: There can be up to two coexistence equilibria, and.

with the properties that

1) the eigenvalues λ_k of A, have, the eigenvalues corresponding with are distinct;

2) is bounded

then the solutions of the system are bounded and is stable in the sense of Lyapunov stability.

Proof: See ( [35] , pages 71-72).

Theorem 2. Consider the system, continuous for with

1) A is a constant matrix with eigenvalues and;

2)

then for all solutions of the system, we have as and Model (2) can be rewritten as

(5)

where, is the vector function of the right hand

side of model (2) with and.

In system (5), by substituting the linearization about the equilibrium, , and using the linear transformation

we get to

where

The general solution of system (6) is of the form, where is the solution of, and is a particular solution of the system. Assume that as. Then, under the conditions of theorem 1 (or similarly theorem 2), the equilibrium remains locally asymptotically stable. Further investigations on the case are left for another study and in the next two subsections we numerically study the model for the case.

3.2. Numerical Verifications

Figure 4(a) shows a numerical verification of model (2) for before and after pro- biotic administration when parameters are set to values which allow for coexistence. The graph was generated by using Matlab’s ODE45 function to verify that the model allows for coexistence at these parameter values. The specific values used are, , , , , , and. All the experimental parameters are set to zero because they are associated with the supplemented probiotics and therefore not involved in the model during times of no probiotic ingestion. Similarly, the coexistence during probiotic administration was verified. As shown in Figure 4(b), a stable spiral was found when, , ,

, , , , ,.

(a) (b)

Figure 4. (a) We used MatlabODE45 to numerically verify the presence of coexistence equilibrium before and after intervention when using the given parameters. The specific parameter values are, , , , , and. All experimental parameters are set to 0. (b) Similarly, the coexistence during probiotic administration is possible. A stable spiral was found when, , , , , , , ,.

Table 4. Summary of the estimated parameter values for before and after probiotics administration and during the administration.

Notes: The Sum of the Squared Error (SSE) was 27.6153 for before and after probiotics administration and 88.6003 during the administration. The negative value of is meaningful due to the fact that.

3.3. Model Fitting

After running MATLAB’s ODE45 and fminsearch. m, the parameter estimations yielding the lowest error were calculated for two cases of presence and absence of probiotics administration. Figure 5 shows the data and the solution curves of the fitted model. Also, the estimated values are shown in Table 4. The values of g and h are both positive during the probiotics administration, which indicate that Bifidobacterium and C. coccoides are cooperative. On the other hand, from and we get that the provided

. Also since and. There- fore, the estimated parameter values suggest that the Bifidobacterium and C. coccoides can be competitive before and after probiotics administration provided. Otherwise (i.e., when), the Bifidobacterium may reduce the growth rate of C. coccoides while it benefits from the presence of C. coccoides. Additionally, adding probiotics promotes the growth of both probiotics and C. coccoides, and their population growth curves are synchronized and oscillatory (see Figure 5 for days 3 - 6).

(a)(b)(c)

Figure 5. Using the Matlab optimization toolbox, the model was fitted to the data, solid and dashed curves represent the model solutions for days 0 - 9. (a) The model solutions represent three spikes, where the spike during the probiotics administration (days 3 - 6) is the highest; (b) the spikes of C. coccoides are synchronized with those of probiotics. The proportions of C. coccoides and probiotics bacteria indicate that they have a cooperative relationship both during and in the absence of probiotics administration; (c) the proportion of all other bacteria is inversely related to those of probiotics and C. coccoides, which suggests a competitive relationship between all other bacteria and the latter two bacterial groups.

4. Discussion

The main objective of this study was to compare the changes in the parameter values before, after, and during the experiment. The primary parameters of interest are, , , and because they are best for showing the interactions between Bifidobacterium and C. coccoides. The computations indicate that when probiotic is not administered (i.e. during normal homeostasis), Bifidobacterium compete against C. coccoides species and inhibit its population growth because. Alternatively, the interactive factor, and therefore indicates that C. coccoides actually helps promote the Bifidobacterium population somewhat albeit with a very small magnitude.

Additionally, this relationship appears to be amplified in the presence of Bifidobacterium supplementation. The parameter g which denotes C. coccoides’ beneficial effect upon Bifidobacterium is significantly greater than h which signifies Bifidobacterium’s beneficial effect upon C. coccoides. Thus, it seems that C. coccoides overall assists Bifidobacterium’s population growth while Bifidobacterium is essentially ambivalent about C. coccoides.

Further of note is that the solution curves of the model indicate that C. coccoides and Bifidobacterium populations move in tandem. Their highs and lows coordinate very well, so they seem to be responding to the same stimulus for growth and decay. However, this study is unable to go into causal factors for why this correlation relationship exists.

Also, despite the fact that our parameter estimations seem to indicate that C. coccoides and Bifidobacterium have beneficial effects upon each other, it should be noted that in the raw data, C. coccoides actually decreases throughout the observation period. This could be due to the residual effects of the supraphysiological levels of Bifidobacterium given during administration and the high value. Next, since canine and human intestinal tracts are largely similar [36] , and their intestinal microbiota are also comparable [37] , it was more convenient to study the effects upon dogs when given probiotics.

In conclusion, the present study suggests that Bifidobacterium and C. coccoides populations move nearly simultaneously and with similar magnitudes. Also, the parameter estimations imply that C. coccoides assist Bifidobacterium populations much more so than Bifidobacterium assist the C. coccoides population. However, further studies are likely needed in order to examine the after supplementation effects of Bifidobacterium administration and how the two population groups interact once supplementation has ceased.

Appendix A

Stability Analysis of Model (2) for the Cases of before and after Probiotics Administration (Case )

The Model is given by:

(1)

(2)

There are four equilibria:

Extinction

Probiotics-free

C. Coccoides-free

Coexistence, where

The Jacobian matrix is given by:

Evaluating the Jacobian matrix at the first equilibrium,

,

which gives the eigenvalues and.

Hence, is stable when:

(C1)

Similarly, for the probiotics-free equilibrium, we have

So, we need to have:

(C2)

Additionally, for the C. coccoides-free equilibrium, we have

which gives the eigenvalues and.

So, we need to have:

(C3)

To determine the stability conditions for the coexistence equilibrium

, first we shift the model to origin by setting and

. We get that:

which has the corresponding Jacobian matrix:

(3)

If, then is unstable.

If, then we need to consider different cases.

We have

(4)

Also, we require that and, where

There are two cases:

If, then only if

(5)

and

(6)

But (2) and (3) imply that, which makes unstable.

If, then only if

(7)

and

(8)

which implies, and therefore is stable.

In summary, (i) is unstable if either

(a) (C4)

Or

(b) (C5)

Moreover,

(C6)

2) is stable only if

, and (C7)

, and (C8)

(C9)

Appendix B

Stability Analysis of the Model for the Case of Probiotics Administration

The model is given by:

(9)

(10)

There are only two possible equilibria:

1) C. coccoides-free equilibrium, where is the root of

. Since we need to have, we must have

and. Since, we get that results in a positive root.

2) Coexistence equilibrium. By setting the right-hand side of (11) equal to zero, we get that:

(11)

Substitute (13) into (12) and set equal to zero.

We get that must satisfy

, where (12)

, and

We need to have to have a real root.

There are four possibilities.

1). Since, there will be a positive root.

2) and. Since, there will be no real roots or two negative roots.

3) and and will produce two positive roots.

Suppose that (14) has a real positive root. Then, we must make sure that in equation (13), i.e..

Stability of:

If we compare model (11), (12) with model (1), (2) on page 1, we get that the Jacobian matrix of model (11), (12) is the same as that of model (1), (2) except for the following changes:

becomes, and

becomes, and

becomes

Hence, following the same procedure, we get that is stable when:

, and

(C10)

We also get that is stable when

, and (C11)

, and (C12)

(C13)

eq(12):, where

Submit or recommend next manuscript to SCIRP and we will provide best service for you:

Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.

A wide selection of journals (inclusive of 9 subjects, more than 200 journals)

Providing 24-hour high-quality service

User-friendly online submission system

Fair and swift peer-review system

Efficient typesetting and proofreading procedure

Display of the result of downloads and visits, as well as the number of cited articles

Maximum dissemination of your research work

Submit your manuscript at: http://papersubmission.scirp.org/

Or contact [e-mail]

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Food and Agriculture Organization/World Health Organization (2002) Guidelines for the Evaluation of Probiotics in Food. Working Group Report on Drafting Guidelines for the Evaluation of Probiotics in Food, London.
[2]	Kleerebezem, M. and Vaughan, E. (2009) Probiotic and Gut Lactobacilli and Bifidobacteria: Molecular Approaches to Study Diversity and Activity. Annual Review of Microbiology, 63, 269-290. https://doi.org/10.1146/annurev.micro.091208.073341
[3]	Backhed, F., Ley, R., Sonnenburg, J., Peterson, D. and Gordon, J. (2005) Host-Bacterial Mutualism in the Human Intestine. Science, 307, 1915-1920. https://doi.org/10.1126/science.1104816
[4]	Hyman, M. (2005) The Real Alternative Medicine: Reconsidering Conventional Medicine. Alternative Therapies, 11, 10-20.
[5]	Arciero, J., Ermentrout, G., Upperman, J., Vodovotz, Y. and Rubin, J. (2010) Using a Mathematical Model to Analyze the Role of Probiotics and Inflammation in Necrotizing Enterocolitis. PLoS ONE, 5, e10066.
[6]	Verna, Elizabeth C. and Lucak, S. (2010) Use of Probiotics in Gastrointestinal Disorders: What to Recommend? Therapeutic Advances in Gastroenterology, 3, 307-319.
[7]	McFarland, L.V. (2006) Meta-Analysis of Probiotics for the Prevention of Antibiotic Associated Diarrhea and the Treatment of Clostridium Difficile Disease. The American Journal of Gastroenterology, 101, 812-822. https://doi.org/10.1111/j.1572-0241.2006.00465.x
[8]	Anukam, K.C. and Reid, G. (2007) Probiotics: 100 Years (1907-2007) after Elie Metchnikoff’s Observation. Communicating Current Research and Educational Topics and Trends in Applied Microbiology, 2, 466-474.
[9]	Simons, L.A., Amansec, S.G. and Conway, P. (2006) Effect of Lactobacillus Fermentum on Serum Lipids in Subjects with Elevated Serum Cholesterol. Nutrition Metabolism and Cardiovascular Diseases, 16, 531-535. https://doi.org/10.1016/j.numecd.2005.10.009
[10]	Reid, G., Jass, J., Subelsky, M.T. and McCormick, J.K. (2003) Potential Uses of Probiotics in Clinical Practice. Clinical Microbiology Reviews, 16, 658-672. https://doi.org/10.1128/CMR.16.4.658-672.2003
[11]	Besselink, M., Santvoort, H., Buskens, E., Boermeester, M., Goor, H., Timmerman, H., et al. (2008) Probiotic Prophylaxis in Predicted Severe Acute Pancreatitis: A Randomized, Double-Blind, Placebo-Controlled Trial. The Lancet, 371, 651-659. https://doi.org/10.1016/S0140-6736(08)60207-X
[12]	Hojsak, I., Pavic, A., Kos, T., Dumancic, J. and Kolacek, S. (2015) Bifidobacterium Animalis Subspecies. Lactis in Prevention of Common Infections in Healthy Children Attending Day Care Centers—Randomized, Double Blind, Placebo-Controlled Study. Clinical Nutrition, 35, 587-591. https://doi.org/10.1016/j.clnu.2015.05.004
[13]	Boswell-Ruys, C.L., Toh, S.L., Lee, B.S.B., Simpson, J.M. and Clezy, K.R. (2013) Probiotics for Preventing Urinary Tract Infection in People with Neuropathic Bladder (Protocol). Cochrane Database of Systematic Reviews, Issue 9, CD010723.
[14]	Rastall, R.A. (2004) Bacteria in the Gut: Friends and Foes and How to Alter the Balance. Journal of Nutrition, 134, 2022-2026.
[15]	Whorwell, P.J., Altringer, L., Morel, J., Bond, Y., Charbonneau, D., O’Mahony, L., Kiely, B., Shanahan, F. and Quigley, E.M.M. (2006) Efficacy of an Encapsulated Probiotic Bifidobacterium Infantis 35624 in Women with Irritable Bowel Syndrome. The American Journal of Gastroenterology, 101, 1581-1590. https://doi.org/10.1111/j.1572-0241.2006.00734.x
[16]	Sokol, H., Seksik, P., Furet, J.P., Firmesse, O., Nion-Larmurier, I., Beaugerie, L., Cosnes, J., Corthier, G., Marteau, P. and Doré, J. (2009) Low Counts of Faecalibacterium Prausnitzii in Colitis Microbiota. Inflammatory Bowel Diseases, 15, 1183-1189. https://doi.org/10.1002/ibd.20903
[17]	Kerckhoffs, A., Samsom, M., Rest, M., Vogel, J., Knol, J., Ben-Amor, K. and Akkermans, L. (2009) Lower Bifidobacteria Counts in Both Duodenal Mucosa-Associated and Fecal Microbiota in Irritable Bowel Syndrome Patients. World Journal of Gastroenterology, 15, 2887-2892.
[18]	Henig, R.M. (2006) Fat Factors. The New York Times, 28-33.
[19]	Shoaie, S., Fredrik, K., Mardinoglu, A., Nookaew, I., Bordel, S. and Nielsen, J. (2013) Understanding the Interactions between Bacteria in the Human Gut through Metabolic Modeling. Scientific Reports, 3, 2532. https://doi.org/10.1038/srep02532
[20]	Clemente, J.C., Ursell, L.K., Parfrey, L.W. and Knight, R. (2012) The Impact of the Gut Microbiota on Human Health: An Integrative View. Cell, 148, 1258-1270.
[21]	Yoshimatsu, Y., Yamada, A., Furukawa, R., Sono, K., Osamura, A., Nakamura, K., et al. (2015) Effectiveness of Probiotic Therapy for the Prevention of Relapse in Patients with Inactive Ulcerative Colitis. World Journal of Gastroenterology, 21, 5985-5994.
[22]	Jia, J., Frantz, N., Khoo, C., Gibson, G.R., Rastall, R.A. and McCartney, A.L. (2010) Investigation of the Faecal Microbiota Associated with Canine Chronic Diarrhoea. FEMS Microbiology Ecology Journal, 71, 304-312. https://doi.org/10.1111/j.1574-6941.2009.00812.x
[23]	Marteau, P., Pochart, P., Dore, J., Bera-Maillet, C., Bernalier, A. and Corthier, G. (2001) Comparative Study of Bacterial Groups within the Human Cecal and Fecal Microbiota. Applied and Environmental Microbiology, 67, 4939-4942. https://doi.org/10.1128/AEM.67.10.4939-4942.2001
[24]	Matsuki, T., Watanabe, K., Fujimoto, J., Takada, T. and Tanaka, R. (2004) Use of 16S Ribosomal Ribose Nucleic Acid (16SrRNA) Gene-Targeted Group Specific Primers for Real-Time Polymerase Chain Reaction Analysis of Predominant Bacteria in Human Feces. Applied and Environmental Microbiology, 70, 7220-7228. https://doi.org/10.1128/AEM.70.12.7220-7228.2004
[25]	Sokol, H., Seksik, P., Rigottier-Gois, L., Lay, C., Lepage, P., Podglajen, I., et al. (2006) Specificities of the Fecal Microbiota in Inflammatory Bowel Disease. Inflammatory Bowel Diseases, 12, 106-111. https://doi.org/10.1097/01.MIB.0000200323.38139.c6
[26]	Honneffer, J., Minamoto, Y. and Suchodolski, J. (2014) Microbiota Alterations in Acute and Chronic Gastrointestinal Inflammation of Cats and Dogs. World Journal of Gastroenterology, 28, 16489-16497. https://doi.org/10.3748/wjg.v20.i44.16489
[27]	Garcia-Mazcorro, J.F., Dowd, S.E., Poulsen, J., Steiner, J. and Suchodolski, J. (2012) Abundance and Short-Term Temporal Variability of Fecal Microbiota in Healthy Dogs. Microbiology Open, 1, 340-347. https://doi.org/10.1002/mbo3.36
[28]	Klappenbach, J.A., Dunbar, J.M. and Schmidt, T.M. (2000) Ribosomal Ribose Nucleic Acid (rRNA) Operon Copy Number Reflects Ecological Strategies of Bacteria. Applied and Environmental Microbiology, 66, 1328-1333. https://doi.org/10.1128/AEM.66.4.1328-1333.2000
[29]	Sun, D.L., Jiang, X., Wu, Q.L. and Zhou, N.Y. (2013) Intragenomic Heterogeneity of 16S Ribosomal Ribose Nucleic Acid (16SrRNA) Genes Causes Overestimation of Prokaryotic Diversity. Applied and Environmental Microbiology, 79, 5962-5969. https://doi.org/10.1128/AEM.01282-13
[30]	Eberl, H.J., Khassehkhan, H. and Demaret, L. (2010) A Mixed-Culture Model of a Probiotic Biofilm Control System. Computational and Mathematical Methods in Medicine, 11, 99-118. https://doi.org/10.1080/17486700902789355
[31]	Kamerman, D.J. and Wilkinson, M.H.F. (2002) In Silico Modelling of the Human Intestinal Microflora. In: Sloot P.M.A., Hoekstra A.G., Tan C.J.K. and Dongarra J.J., Eds., Computational Science—ICCS 2002, Lecture Notes in Computer Science, Vol. 2329, Springer, Berlin, Heidelberg, 117-126. https://doi.org/10.1007/3-540-46043-8_11
[32]	Reynolds, A., Rubin, J., Clermont, G., Day, J., Vodovotz, Y. and Ermentrout, G.B. (2006) A Reduced Mathematical Model of the Acute Inflammatory Response: I. Derivation of Model and Analysis of Anti-Inflammation. Journal of Theoretical Biology, 242, 220-236. https://doi.org/10.1016/j.jtbi.2006.02.016
[33]	Wilkinson, M.H.F. (2002) Model Intestinal Microflora in Computer Simulation: A Simulation and Modeling Package for Host-Microflora Interactions. IEEE Transactions on Biomedical Engineering, 49, 1077-1085. https://doi.org/10.1109/TBME.2002.803548
[34]	Geijzendorffer, I.R., Werf, W.V.D., Bianchi, F.J.J.A. and Schulte, R.P.O. (2011) Sustained Dynamic Transience in a Lotka-Volterra Competition Model System for Grassland Species. Ecological Modelling, 222, 2817-2824.
[35]	Verhulst, F., (2006) Nonlinear Differential Equations and Dynamical Systems. 3rd Edition, Springer-Verlag, New York.
[36]	Dressman, J. (1986) Comparison of Canine and Human Gastrointestinal Physiology. Pharmaceutical Research, 3, 123-131. https://doi.org/10.1023/A:1016353705970
[37]	Clapper, W.E. and Meade, G.H. (1963) Normal Flora of the Nose, Throat, and Lower Intestine of Dogs. Journal of Bacteriology, 85, 643-648.