Study and Optimization of a Photovoltaic Mill System Functioning on the Course of the Sun ()
1. Introduction
Currently, solar photovoltaic is no longer limited to lighting or powering domestic appliances; but it also supplies income generating activities, particularly solar grain mill [1] . Unfortunately, the solar panels offered by manufacturers are still expensive, despite many efforts do by researchers to improve the efficiency and reduce the cost of photovoltaic cells [2] . That’s why the use of a solar mill running in remote areas is the subject of our study which has a purpose of optimizing the system.
The use of a photovoltaic generator (PVG) must be subjected to some requirements:
The system should be as simple as possible;
The photovoltaic generator must be optimized with a correct efficiency;
The system must operate automatically and reliably.
The simplest system we can have in this case is to directly couple the PV generator to a DC load (DC motor-mill group for example). But generally, the operating point of the DC load does not match the optimum operating point of the PVG [3] [4] [5] . This means that all the energy produced by the PVG is not transmitted to the load.
That’s why we are interested to sizing of a solar system operating mill running over the sun. In order to optimize the system performance, we use a matching circuit consisting of a boost converter controlled by MPPT (Maximum Power Point Tracking) control.
In our work, we proposed a modeling study under MATLAB/Simulink for the various components of the PV system and we presented the simulation results which are discussed.
2. Modelization of Photovoltaic System
The system studied is composed of a PV generator, a boost converter, a PWM controller with MPPT technology and a DC motor-mill group. The following Figure 1 shows the block diagram of the overall system:
The matching circuit is a boost converter inserted between the PV field and the DC load and which maximizes the power supplied to the load for any level of illumination and temperature thanks to the digital MPPT control.
2.1. Modelization of PV Generator
The power delivered by a photovoltaic cell is not enough to supply a DC load like motor-mill group. It is necessary to associate multiple solar cells in series
![]()
Figure 1. Block diagram of a PV system with boost converter controlled MPPT on a DC load.
and in parallel to have a solar panel and attain the desired power. Similarly, the interconnection of several solar panels in series and in parallel enables to obtain a power higher than that of the solar panel; that is why the notion of PV generator is created [6] .
If we set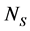 , the number of solar panels in series in a branch and
, the number of solar panels in series in a branch and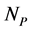 ,the number of parallel branch, then the electrical diagram of the PV generator can be represented in Figure 2.
,the number of parallel branch, then the electrical diagram of the PV generator can be represented in Figure 2.
The relationship between the current Ipv (A) and the voltage Vpv (V) at the output of the PVG constituted by several panels connected in series and in parallel is modeled in the literature by [7] :
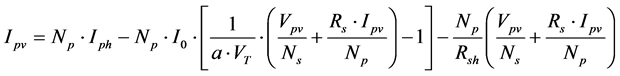 (1)
(1)
where:
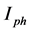 : The photocurrent produced by the cell;
: The photocurrent produced by the cell;
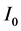 : The saturation current of the diode;
: The saturation current of the diode;
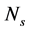 : Number of solar panels connected in series;
: Number of solar panels connected in series;
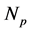 : Number of solar panels connected in parallel;
: Number of solar panels connected in parallel;
 : The thermal potential;
: The thermal potential;
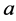 : The ideality factor (we set
: The ideality factor (we set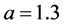 ).
).
The equation of the photocurrent (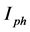 ) is given by:
) is given by:
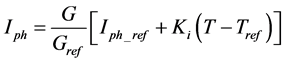 (2)
(2)
where,
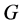 : Solar irradiation (W/m²);
: Solar irradiation (W/m²);
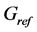 : Solar irradiation of reference (1000 W/m2);
: Solar irradiation of reference (1000 W/m2);
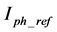 : The photocurrent in the STC (25˚C, 1000 W/m2);
: The photocurrent in the STC (25˚C, 1000 W/m2);
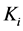 : Coefficient of variation of current (A/˚C);
: Coefficient of variation of current (A/˚C);
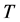 : The absolute temperature in kelvin (K);
: The absolute temperature in kelvin (K);
![]() : The reference temperature (25˚C).
: The reference temperature (25˚C).
The saturation current of the diode is given by the following equation:
![]()
Figure 2. Synoptic electrical diagram of the PV generator.
![]() (3)
(3)
![]() : Open circuit voltage of the solar cell in the STC (25˚C; 1000 W/m²);
: Open circuit voltage of the solar cell in the STC (25˚C; 1000 W/m²);
![]() : Coefficient of variation of voltage (V/˚C).
: Coefficient of variation of voltage (V/˚C).
From these equations, the model of PV generator is made using Simulink software.
2.2. Modelization of Boost Converter
The boost converter is an elevator DC-DC converter inserted between the PVG and the DC load. Its typical application is to convert the input voltage to a higher output voltage [4] [8] . The basic components of a boost converter are: a diode D, a MOSFET transistor Tr which takes two states (closed (u = 1) and open (u = 0)), an inductor L and an output capacitor Cs. The basic scheme of the boost converter is shown in Figure 3.
When the transistor Tr is closed (on mode), the photovoltaic source charges the inductance L, meanwhile, the capacitor Cs maintains the output voltage of the converter using the energy previously stored. When the position of the transistor Tr change (off mode), the DC source and the energy stored in the inductance go together supply the load, resulting in an increase of the output voltage [4] .
The modeling of the boost converter can be obtained by applying the fundamental laws governing its operation [8] :
![]() (4)
(4)
and
![]() (5)
(5)
During the hash period, the transformation ratio is, by calling α duty cyclic (i.e. ratio of the time during which the transistor is closed [5] [8] ):
![]() (6)
(6)
With α taking values comprised between 0 and 1.
![]()
Figure 3. Electrical diagram of the boost converter.
For a given incident power, the optimum power transferred to the load is maximum only for a well-defined duty cyclic.
2.3. Modelization of Digital MPPT Control: “P & O” Method
In this study, we used the Perturbation and Observation (P & O) method. This choice is due to the fact that this is a widespread approach in seeking the MPP (Maximum Power Point); in addition it is simple to use and requires only measurements of current and voltage of the PV generator (![]() and
and![]() ). It is based on the periodic disturbance of the system by increasing or decreasing the reference voltage (
). It is based on the periodic disturbance of the system by increasing or decreasing the reference voltage (![]() ) or by directly acting on the duty cyclic α of the converter, and then observing the effect on the output power in order to a possible correction of the duty cyclic [4] and [7] . Figure 4 shows the flow chart of the control algorithm “Perturbation and Observation” as it should be implemented in the microprocessor control.
) or by directly acting on the duty cyclic α of the converter, and then observing the effect on the output power in order to a possible correction of the duty cyclic [4] and [7] . Figure 4 shows the flow chart of the control algorithm “Perturbation and Observation” as it should be implemented in the microprocessor control.
2.4. Modelization of PWM Control
The reference voltage thus generated by the MPPT control is then compared with a triangular (or sawtooth) signal in order to provide an adequate duty cyclic. This principle is called PWM (Pulse Width Modulation) controller [4] . (Figure 4)
A comparator makes it possible to generate at its output a rectangular voltage modulated in impulsion width. (Figure 5)
![]()
Figure 4. The structure of the MPPT algorithm “Perturbation and Observation”.
![]()
Figure 5. Generation of a square signal at the output of the comparator.
When the voltage Vref increases (decreases), the duty cyclic increases (decreases). The variations of the voltage, Vref, induce, for a given sunshine and temperature, a move of the operating point on the Ppv/Vpv characteristic curve.
2.5. Modelization of the DC Motor-Mill Group
DC Motors are used for the training of electrical machines. In our study it is a grain mill. The motor shaft is connected to the hammers of mill via a polished- belt system. The block diagram of such DC load is presented in Figure 6.
The DC machine can be modeled through electrical, electromagnetic and mechanical equation. These three groups of equations describe the real operation of the DC motor:
Ø Electrical equation [9] :
![]() (7)
(7)
where:
![]() (V) is the supply voltage of the motor armature;
(V) is the supply voltage of the motor armature;
![]() (A) is the current drawn by the armature;
(A) is the current drawn by the armature;
![]() (Ω) is the resistance of the armature;
(Ω) is the resistance of the armature;
![]() (H) is the inductance of the armature;
(H) is the inductance of the armature;
![]() (V) is the electromotive force.
(V) is the electromotive force.
The electromotive force (E) is related by the rotational speed of the motor by the relation:
![]() (8)
(8)
where:
![]() : is a specific constant of the motor;
: is a specific constant of the motor;
![]() (Weber) is the magnetic flux;
(Weber) is the magnetic flux;
![]() (V/rad/s) is constant of electromagnetic force;
(V/rad/s) is constant of electromagnetic force;
![]() (rad/s) is the rotation velocity of the motor.
(rad/s) is the rotation velocity of the motor.
Ø Electromagnetic equation [9] :
![]()
Figure 6. Schematic diagram of the DC motor.
When a current Ia circulates in the armature of the motor, there appears an electromagnetic torque Tem (N·m) created by the Laplace forces which are exerted on the conductors of the armature. This torque is related to the inductor flux ![]() and the current in the armature by the relation [9] :
and the current in the armature by the relation [9] :
![]() (9)
(9)
If the armature presents an electromotive force E, while it is traversed by a current of intensity![]() , then the motor receives an electromagnetic power Pem:
, then the motor receives an electromagnetic power Pem:
![]() (10)
(10)
The rotor turns at the angular velocity Ω. Hence the power Pem can also be written as:
![]() (12)
(12)
Ø Mechanical equation :
The mechanical equation of the electric motor described the ratio between the moment of inertia J (kg·m2), the rotational speed Ω (rad/s) and the torque T (N·m). By equating the motor torque to the electromagnetic torque (true to a constant: friction torque), this equation is given in [9] by:
![]() (13)
(13)
![]() : is the load torque;
: is the load torque;
![]() : is the inertia moment (Motor + training load);
: is the inertia moment (Motor + training load);
![]() : is the coefficient of friction proportional to the rotational velocity.
: is the coefficient of friction proportional to the rotational velocity.
3. Simulation Results and Discussions
3.1. Simulation Results of PVG
The results obtained after simulation of the PV generator are shown in Figure 7, it represents the current?voltage (I-V) and power-voltage (P-V) characteristics curves of the PV generator under standard test conditions (![]() ,
,![]() ):
):
![]()
![]()
Figure 7. Simulation results of the I-V and P-V characteristic curves of PV generator for G = 1000 W/m2 and T = 25˚C.
These results show the nonlinearity characteristics of the PV generator. Indeed, on the characteristic curve I-V (or P-V), there is a point where the power delivered by the PV generator is maximum (![]() ,
,![]() and
and![]() )
)
In order to know the effect of the temperature on the performance of the PV system, we presented in the Figure 8 the I-V and P-V characteristics curves for a constant sunshine level (![]() ) and for different temperatures.
) and for different temperatures.
We can see that the increase of temperature causes a small drop in the power available at the terminals of the PV generator.
For to know the effect of solar radiation on the I-V and P-V characteristics curves of the PV generator, we set the temperature at![]() and vary the amount of sunlight from 400 to 1000 W/m2. We get the following results: (Figure 9).
and vary the amount of sunlight from 400 to 1000 W/m2. We get the following results: (Figure 9).
These results show that the current produced by the PV generator is highly
![]()
![]()
Figure 8. Simulation results of the influence of temperature on the I-V and P-V characteristics curves of the PV generator to Gref = 1000 W/m2.
dependent on solar radiation, but the voltage varies slightly. Then the maximum power point (MPP) of PV generator varies with decreasing sunlight.
3.2. Simulation Results of the Boost Converter
The simulation using the MATLAB/Simulink software made it possible to have the
![]()
![]()
Figure 9. Simulation results of the influence of sunlight on the I-V and P-V characteristics curves of the PV generator to Tref = 25˚C.
results presented in Figure 10. These figure shows the signal applied to the gate of the transistor which corresponds to a switching frequency set at 50%.
In Figure 11, we show the input and output voltage of the boost converter after simulation.
These results show that the output voltage of the converter is higher than that the input. So the DC-DC converter performs its role properly.
3.3. Simulation Results of Direct Coupling PVG-DC Load
The simulation results for the direct connection between the PVG and the DC load are shown in Figure 12 which gives the I-V characteristic curve of the PVG superimposed on the I-V characteristic curve of the load. These results show that the operating point in direct coupling does not match the maximum power point of the PV generator.
![]()
Figure 10. Simulation result of the converter control signal.
![]()
Figure 11. Simulation results of the input and output voltage of the boost converter.
![]()
Figure 12. Simulation results of I-V characteristics curves in direct coupling.
We can observe that the PV generator is poorly operated and does not provide the maximum potential power. The difference being wasted as heat dissipated in the PVG. This can be explained by the fact that the nominal operating voltage of the load is different from the optimum voltage Vopt of PVG.
With the measured values of the PVG characteristics (![]() and
and![]() ), we have:
), we have:![]() ,
, ![]() and
and![]() .
.
Direct connection was simulated output power and gives as results:![]() ,
, ![]() and
and![]() .
.
In this case, there is an efficiency of:
![]()
3.4. Simulation Results of System Optimized by the MPPT Technology (P & O)
The obtained results are represented in Figure 13 which gives the I-V characteristic curve of the PVG superimposed on the I-V characteristic one of the load.
These results show that the operating point of the system converges to the maximum power point of the PV generator.
The optimized system gives as results:
![]()
Hence the efficiency of the system is: ![]()
4. Conclusions
In this paper, we modeled and simulated all the components of a solar mill system: PV generator, boost converter, MPPT control “Perturbation and Observation” and the load (DC motor-mill group). The simulation results and discussions for direct connection PVG-load and indirect connection controlled by a DC/DC converter are presented. From these results, we noted that:
![]()
Figure 13. Simulation results of the I-V characteristic curves of the system optimized by MPPT.
The performances of PVG degrade with fluctuations of weather conditions (temperature and illumination);
The boost converter and the MPPT control (P & O) properly perform their role. The boost converter provides an output voltage higher than the input voltage; and the MPPT control adjusts the PV generator to the load: There’s a maximum transfer of the available power to the terminals of the PV generator.