Effects of Inflow Conditions on Wind Turbine Performance and near Wake Structure ()
1. Introduction
The turbulent wake behind a horizontal axis wind turbine is mainly charac- terized by a helical system of tip vortices, a mean velocity deficit and a tur- bulence distribution. The low velocity and high turbulence levels in the wake cause a reduced power output and increased loadings for the downwind turbines in wind power farms. Hence, knowledge about the development of wind turbine wakes is important for optimization of wind power farms, both in terms of power output and lifetime of the farm. The wake behind a turbine is often divided into the near wake (up to approximately 1 - 2 downstream diameters) and the far wake (from 1 - 2 downstream diameters) [1] . In wind power farms, the average distance between the turbines is usually more than 3 - 4 diameters. Most of the research is therefore focused on the far wakes, where the subsequent turbines are placed. This is also a simpler region to construct a general model for, since it is less dependent on the specific blade aerodynamics of the turbine. The near wake constitutes however the boundary conditions for the far wake, and the specific structure and dynamics of the near wake is therefore also important in the strive for increased knowledge of turbine wakes.
There are a number of models used to describe the development of wind turbine wakes. In the simplest models, a linear spreading of the wake is assumed and the mean velocity deficit in the wake is often considered to have a power- law decay [1] . A standard bluff-body wake is also often used, with a spreading proportional to the square root of the downstream distance. In many analytical models and numerical simulations, the wake is also assumed to be axisymmetric. This is in reality not the case, since the turbine tower and also the ground is affecting the wake.
Full-scale experiments and measurements in the field is expensive and often suffer from fluctuating or unknown boundary conditions. Experimental research on small-scale models placed in wind tunnels or water channels therefore cons- titute a significant part of the ongoing research within this field. Both types of experiments is also needed for validation studies of numerical models.
For experiments and simulations, it is tempting to assume a uniform inflow for simplicity. However, since full-scale operating turbines are placed inside the atmospheric boundary layer, the influence and effects of a boundary layer inflow are important research topics. [2] studied the near wake structure of a wind turbine placed in a neutral boundary layer flow. The model was placed in the lowest one-third of the boundary layer, and both Particle Image Velocimetry (PIV) and hot-wire measurements were performed up to 5 downstream dia- meters (using PIV) and 20 downstream diameters (using hot-wire). The near wake results revealed a high three-dimensionality of the flow, with a strong flow rotation. Immediately behind the turbine, a strong decrease of the streamwise velocity was present, while the other two velocity components increased. With an increasing downstream distance, the streamwise velocity then recovered, while the other components decreased again. [3] also performed a comparative wind tunnel study between a neutral and convective boundary layer. An enhanced turbulence intensity and a smaller velocity deficit was found in the latter case, where the enhanced radial momentum transport caused a more rapid wake re- covery. This shows the potential importance of taking thermal stability into account in the wind farm design process, since it might effect both power output and fatigue loads. [4] compared turbulence statistics in the wake of a model turbine, with a neutral boundary layer inflow and stably stratified conditions. In the neutral case, a maximum of the turbulent intensity was found above the rotor, approximately at tip height, between 4 - 5.5 rotor downstream diame- ters. In the stable case, the stronger shear led to a slightly larger turbulence intensity above hub height, as well as an enlarged region of enhanced turbulence intensity.
The near wake structures behind a model turbine were characterized in a wind tunnel study by [5] , where velocity measurements using PIV, and direct force measurements using a high-sensitive force-moment sensor were performed. The results showed highly unsteady loads, which instantaneously could be as high as 2 - 3 times the time-averaged values. [6] made a comparison between boundary layer inflows developed over rough and smooth surfaces, respectively. In res- ponse to the non-uniform inflow, a non-axisymmetric behaviour of the wake was found. However, the velocity deficit was found to be nearly axisymmetric with respect to the incoming boundary layer profile. The wind turbine model also caused increased turbulence levels in the upper part of the wake, while both the mean shear and the turbulence intensity in the lower part were reduced with respect to the incoming flow. The latter effect was more prominent in the rough surface case.
One of the major problems with wind tunnel studies on small scale turbines is the significantly lower Reynolds number as compared to full scale. Most studies have models with diameter in the order of 100 - 300 mm, even though there are some exceptions with markedly larger turbines (see e.g. the MEXICO project with a rotor diameter of 4.5 m [7] ). It has however been suggested by [8] that the vortex and turbulent flow structures are almost independent of the chord Reynolds number, making these features suitable for wind tunnel studies. A previous study with the same type of model as the one used in the present study did not show any Reynolds number dependence in the streamwise mean velocity and turbulence intensity profiles in the wake. However, a clear Reynolds number effect on the power output in the studied Reynolds number range has been reported [9] . The model in these studies did however have different airfoil blades than the one used in the present study. [10] performed a study where the Reynolds number based on model diameter and hub velocity was varied in the range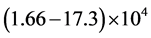 . The mean velocity and turbulence intensity became independent of the Reynolds number starting from
. The mean velocity and turbulence intensity became independent of the Reynolds number starting from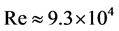 . Stronger Reynolds number dependence was in general found in the near wake region, where the wake is still affected by the blade aerodynamics.
. Stronger Reynolds number dependence was in general found in the near wake region, where the wake is still affected by the blade aerodynamics.
The turbulence inside wind farms is a complex interaction between the atmos- pheric boundary layer turbulence and the turbulence generated inside the farm. The momentum transfer between the boundary layer and the flow within arrays of wind turbines is not yet fully understood and the flow statistics are affected a long distance behind a wind turbine. In the wind tunnel study by [4] , effects were measured 20 rotor diameters downstream of the model turbine. Based on wind tunnel data, [11] showed that a turbine produces high turbulent kinetic energy into the wake, and acts like a turbulence generator. The large scales were however found to be dampened in the wake. It was suggested that the turbine acts like a filter, amplifying some frequencies and dampening others. Also [12] studied the turbulence kinetic energy budget (turbulence kinetic energy and dissipation rate) in wind turbine wakes, using both experimental data and numerical results. Simple analytical expressions were proposed, which gave a reasonable agreement with the numerical and experimental results.
In the study of wake interaction effects, it is obviously important to consider multiple models. Such a study was performed by [13] , where the effects by varying the distance between two turbines was studied. Furthermore, the operating conditions (power extraction and yaw angle) of the upstream turbine were varied to investigate the influence on the downstream one. The power loss in the downstream turbine varied between 29% - 46% as compared to an un- disturbed turbine, when the distance between them was varied from 9 to 3 rotor diameters. [14] studied the vertical transport of momentum and kinetic energy in a 3 × 3 array of model turbines. The aim was to better understand the interaction between the atmospheric boundary layer and arrays of wind turbines. The mean velocity and turbulence properties were studied on hori- zontally averaged planes, and it was found that the fluxes of kinetic energy asso- ciated with the Reynolds shear stresses were of the same order of magnitude as the power extracted by the wind turbines.
Many experiments have been performed with small scale model turbines. In summary, it can be concluded that small scale turbine model experiments are heavily model dependent, both in terms of mean velocity deficit and turbulence levels. This is especially true in the near wake, where the flow is inherently coupled to the blade aerodynamics. The structure of the wake is therefore depen- dent on the specific airfoil used. The upscaling from wind tunnel scale is not straight forward, and there is a need for several experiments with different air- foils and at different Reynolds numbers to be able to draw conclusions regarding possible upscaling effects. Even though each experiment can be used separately, for CFD (Computational Fluid Dynamics) validation or parameter studies, there is a need for several experiments in order to be able to draw general conclusions regarding wind turbine wakes. The purpose of the present study is to provide detailed experimental data in the near wake of a wind turbine model. To this purpose, we have performed PIV measurements, between 0.4 and 3.0 rotor radius, behind a model wind turbine. Two cases with different inlet conditions were compared. The first case had an inflow consisting of a freely developing boundary layer, which caused an almost uniform inflow across the rotor disc. For the second case, roughness elements and triangular spires were inserted at the beginning of the test section, in order to simulate an atmospheric boundary layer inflow. This resulted in a power-law profile across the rotor disc as well as significantly higher turbulence levels at the inlet. Results are presented for both power and thrust coefficients, as well as detailed PIV data in the wake. For validation, also a comparison with hot-film measurements is presented.
2. Experimental Setup
2.1. Wind Tunnel
The measurements were performed in the atmospheric wind tunnel at the University of Gävle. The wind tunnel facility is a closed loop tunnel with a total length of 28 m and a maximum velocity in the test section of 22 m/s. The contraction ratio is 3:1 and the tunnel is driven by a 45 kW fan placed in the return circuit. The tunnel is equipped with guiding vanes and honeycombs to improve the flow quality. The size of the measurement section is 11 × 3 × 1.5 m3 (length × width × height).
A right-handed coordinate system for the setup is used, which has its origin at the centre of the model at hub height, with  as the streamwise coordinate (positive downstream),
as the streamwise coordinate (positive downstream), 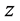 as the vertical coordinate (positive upwards) and
as the vertical coordinate (positive upwards) and  as the spanwise coordinate. The mean streamwise velocity is denoted by
as the spanwise coordinate. The mean streamwise velocity is denoted by 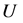 and its root-mean-square value of the fluctuations with
and its root-mean-square value of the fluctuations with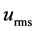 . The corresponding notation for the vertical component is
. The corresponding notation for the vertical component is  and
and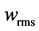 . The velocity is scaled with the velocity at hub height,
. The velocity is scaled with the velocity at hub height, 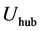 , which is here taken as the mean value over the whole rotor disc. In order to comply with standard boundary layer theory, the inlet profiles are shown with a different vertical coordinate
, which is here taken as the mean value over the whole rotor disc. In order to comply with standard boundary layer theory, the inlet profiles are shown with a different vertical coordinate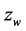 , where the origin is set at the wind tunnel floor. The free-stream velocity is denoted by
, where the origin is set at the wind tunnel floor. The free-stream velocity is denoted by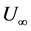 .
.
2.2. Turbine Model
A three bladed turbine model with a hub height of  and a sweep area diameter of
and a sweep area diameter of  was used. The turbine blades were designed using an in-house blade element momentum (BEM) code, using the Glauert optimization [15] [16] . The airfoil profile was an SD7003 and the design opti- mization was made for a tip speed ratio
was used. The turbine blades were designed using an in-house blade element momentum (BEM) code, using the Glauert optimization [15] [16] . The airfoil profile was an SD7003 and the design opti- mization was made for a tip speed ratio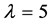 . The tip speed ratio is defined as the speed of the blade tip divided by the hub velocity
. The tip speed ratio is defined as the speed of the blade tip divided by the hub velocity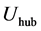 :
:
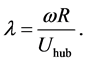 (1)
(1)
Here, 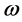 is the angular velocity, making
is the angular velocity, making ![]() the speed of the blade tip. The blades were manufactured of aluminium which was then painted black to mini- mize reflections from the PIV laser. The total twist was 31˚ and the chord length varied from 31 mm close to the hub to 15 mm close to the blade tip. The pitch angle at the tip was set to 3.3˚. The chord Reynolds number (based on chord length and relative velocity) varied from 15,000 close to the hub to 26,000 close to the tip, with an average of 22,000. The blockage ratio (swept area of the rotor divided by the cross-sectional area of the wind tunnel) was 0.9%, which is far below the suggested upper limit of 10% to avoid effects on the wake expansion due to tunnel wall interference [17] . Therefore, no blockage correction methods were applied to compensate for the presence of the wind tunnel walls.
the speed of the blade tip. The blades were manufactured of aluminium which was then painted black to mini- mize reflections from the PIV laser. The total twist was 31˚ and the chord length varied from 31 mm close to the hub to 15 mm close to the blade tip. The pitch angle at the tip was set to 3.3˚. The chord Reynolds number (based on chord length and relative velocity) varied from 15,000 close to the hub to 26,000 close to the tip, with an average of 22,000. The blockage ratio (swept area of the rotor divided by the cross-sectional area of the wind tunnel) was 0.9%, which is far below the suggested upper limit of 10% to avoid effects on the wake expansion due to tunnel wall interference [17] . Therefore, no blockage correction methods were applied to compensate for the presence of the wind tunnel walls.
The nacelle consisted of a small electricity generator, which was connected to a known resistance and a variable number of diodes through a Wheatstone bridge. The current through the circuit was calculated by measuring the voltage over the resistance. By applying different loads (i.e. different number of diodes in the electrical circuit), the rotational frequency of the model could be varied from 800 to 4200 rpm, corresponding to a change in tip speed ratio from 1.6 to 8.3, with a fixed free-stream velocity. To avoid taking the electrical losses in the generator into account, the power output, ![]() , was calculated as the rotational torque,
, was calculated as the rotational torque, ![]() , multiplied by the angular velocity,
, multiplied by the angular velocity,![]() . The generator had a torque,
. The generator had a torque, ![]() , versus current,
, versus current, ![]() , relationship of the form
, relationship of the form![]() , where
, where ![]() and
and ![]() are calibration constants. The rotational frequency was measured with a laser emitter and receiver. The laser was aligned so that each passage of a blade blocked the laser, thus causing a pulse signal from the receiver. The thrust force
are calibration constants. The rotational frequency was measured with a laser emitter and receiver. The laser was aligned so that each passage of a blade blocked the laser, thus causing a pulse signal from the receiver. The thrust force ![]() was measured by placing the model on a VETEK load cell.
was measured by placing the model on a VETEK load cell.
2.3. Velocity Measurement Techniques
Hot-film measurements were performed with a single component probe of ![]() wire diameter. It was calibrated against a known differential pressure by measuring 15 points and then fitting the points to a polynomial curve. A standard temperature correction was applied, since the tunnel did not have any temperature control at the time.
wire diameter. It was calibrated against a known differential pressure by measuring 15 points and then fitting the points to a polynomial curve. A standard temperature correction was applied, since the tunnel did not have any temperature control at the time.
A Particle Image Velocimetry (PIV) system consisting of a HI Sense Mk II camera (1344 × 1024 pixels) and a laser was used. The physical size of each image was 100 × 77 mm2. For the evaluation, an adaptive correlation scheme was used, with 50% overlap and an interrogation area of 32 × 32 pixels. The sampling frequency was 6.1 Hz. Measurements were made in the region ![]() and
and ![]() at three different spanwise positions:
at three different spanwise positions: ![]() and
and![]() , corresponding to the centreline, middle of the wake and edge of the wake. Here,
, corresponding to the centreline, middle of the wake and edge of the wake. Here, ![]() corresponds to the radius of the rotor sweep area. A sketch of the setup, coordinate system and the measured planes are shown in Figure 1.
corresponds to the radius of the rotor sweep area. A sketch of the setup, coordinate system and the measured planes are shown in Figure 1.
2.4. Inlet Boundary Conditions
Two cases with different inlet boundary conditions were compared. The first case had a naturally developing boundary layer along the test section. In this case, both the mean velocity and the turbulence intensity had an almost uniform
![]()
Figure 1. A sketch of the setup, coordinate system and the measured planes.
distribution across the rotor disc (except for the lowest part). This case is here denoted “naturally developing boundary layer (NBL) inflow”, and will be abbreviated the “NBL case”. For the second case, a thicker boundary layer was created by adding triangular spires in the beginning of the test section, followed by several meters of roughness elements. This was done in order to mimic the atmospheric boundary layer (ABL), and this case will therefore be denoted the “atmospheric boundary layer inflow”, abbreviated as the “ABL case”. In this case, the rotor was subjected to an inflow with strong shear and higher turbulence levels as compared to the NBL case. A picture of the wind tunnel test section with the spires and roughness elements can be seen in Figure 2. For the NBL case, the test section was empty (except for the turbine model), giving rise to a significantly thinner boundary layer compared to the ABL case. The velocity at hub height ![]() was 6.0 m/s in the NBL case and 4.2 m/s in the ABL case. The corresponding streamwise turbulence intensities (
was 6.0 m/s in the NBL case and 4.2 m/s in the ABL case. The corresponding streamwise turbulence intensities (![]() ) were 1.3% and 15%, respectively. Both the hub velocities and the turbulence intensities are taken as the mean values over the whole rotor disc.
) were 1.3% and 15%, respectively. Both the hub velocities and the turbulence intensities are taken as the mean values over the whole rotor disc.
Figure 3 shows the inlet profiles, measured with hot-film and PIV. The profiles are measured at the position of the turbine, but in absence of the turbine itself. The PIV data have been high-pass filtered using a cut-off frequency based on the longest length scale, which locally can affect the boundary layer, i.e. the sum of the height and width of the cross section of the tunnel (1.5 + 3.0 = 4.5 m) and the velocity at![]() , which was
, which was![]() . This gave a cut-off fre- quency of
. This gave a cut-off fre- quency of![]() . For the ABL case, a power law fit has been added over the rotor disc location, according to the following equation:
. For the ABL case, a power law fit has been added over the rotor disc location, according to the following equation:
![]() (2)
(2)
![]()
Figure 2. Picture of the wind tunnel looking upstream with the turbine model and the roughness elements and spires used to create the atmospheric boundary layer.
where ![]() is the mean streamwise velocity at height
is the mean streamwise velocity at height ![]() above the tunnel floor and
above the tunnel floor and ![]() is the velocity at hub height,
is the velocity at hub height,![]() . In atmospheric boundary layer theory,
. In atmospheric boundary layer theory, ![]() is normally considered to be around
is normally considered to be around![]() , and in cases of extreme shear up to
, and in cases of extreme shear up to![]() . For the current data, the fit gave
. For the current data, the fit gave![]() , making this a fairly sheared profile across the rotor disc. For both cases, a log law fit was made closest to the floor according to:
, making this a fairly sheared profile across the rotor disc. For both cases, a log law fit was made closest to the floor according to:
![]() (3)
(3)
where ![]() is the friction velocity,
is the friction velocity, ![]() is the von Kármán constant and
is the von Kármán constant and ![]() is the surface roughness length. The friction velocity is defined as
is the surface roughness length. The friction velocity is defined as![]() , where
, where ![]() is the skin friction and
is the skin friction and ![]() is the air density. A least squares log law fit gave
is the air density. A least squares log law fit gave ![]() and
and ![]() (NBL case) and
(NBL case) and ![]() and
and ![]() (ABL case). For comparison, the friction velocity was found to be between 0.06 and 0.11 m/s in a field experiment with
(ABL case). For comparison, the friction velocity was found to be between 0.06 and 0.11 m/s in a field experiment with ![]() [18] .
[18] . ![]() for the present experiment was
for the present experiment was ![]() and
and![]() , for the NBL and ABL cases, respectively. For a very smooth surface (ice or mud),
, for the NBL and ABL cases, respectively. For a very smooth surface (ice or mud), ![]() is generally set to 0.01 mm [19] . The free-stream velocity, the hub velocity, the displacement thickness
is generally set to 0.01 mm [19] . The free-stream velocity, the hub velocity, the displacement thickness![]() , the momentum thickness
, the momentum thickness ![]() and the shape factor
and the shape factor ![]() for both cases are summarized in Table 1. Included is also an estimation of the shear across the rotor disc,
for both cases are summarized in Table 1. Included is also an estimation of the shear across the rotor disc, ![]() , i.e. the change in mean velocity over the turbine disc location.
, i.e. the change in mean velocity over the turbine disc location.
The inlet streamwise turbulence intensities for the two cases are shown in
![]()
![]()
Figure 3. Inflow conditions: mean streamwise velocity for (a) the NBL case and (b) the ABL case. The power law and log law in (b) are calculated according to Equation (2) and (3), respectively.
![]()
Table 1. Description of the inflow boundary layer for the two cases NBL and ABL.
Figure 4. Note that Figure 3 and Figure 4 are shown with the origin at the wind tunnel floor (the vertical coordinate is therefore denoted![]() ) and that
) and that ![]() is scaled by the hub height
is scaled by the hub height![]() . In the rest of the paper, the results are shown with the origin at hub height of the model and the vertical coordinate scaled with the rotor radius.
. In the rest of the paper, the results are shown with the origin at hub height of the model and the vertical coordinate scaled with the rotor radius.
3. Wind Turbine Model Measurements
3.1. Power and Thrust Measurements
The power and thrust coefficients are defined as:
![]() (4)
(4)
where ![]() is the power output from the turbine,
is the power output from the turbine, ![]() is the total thrust force and
is the total thrust force and ![]() is the sweep area of the rotor,
is the sweep area of the rotor,![]() . The measured power and thrust coefficients are plotted in Figure 5. All the following velocity measurements were performed at a tip speed ratio of 5, corresponding to the tip speed ratio the blades were optimized for. This gave
. The measured power and thrust coefficients are plotted in Figure 5. All the following velocity measurements were performed at a tip speed ratio of 5, corresponding to the tip speed ratio the blades were optimized for. This gave ![]() and
and ![]() for the NBL case and
for the NBL case and ![]() and
and ![]() for the ABL case. These values were expected, since small-scale model turbines usually perform somewhat worse than full scale ones, with a lower maximum power output and a higher thrust. Due to the small-scale in the wind tunnel, the optimal tip speed ratio is also often lower than for full scale turbines. It can be seen in Figure 5 that the power output in the NBL case is slightly higher than in the case with ABL inflow, while the thrust coefficients remains approximately the same. It is not clear whether the difference is due to the shear layer and/or increased turbulence or if it is a Reynolds number effect. The Reynolds numbers based on hub velocity and rotor diameter were
for the ABL case. These values were expected, since small-scale model turbines usually perform somewhat worse than full scale ones, with a lower maximum power output and a higher thrust. Due to the small-scale in the wind tunnel, the optimal tip speed ratio is also often lower than for full scale turbines. It can be seen in Figure 5 that the power output in the NBL case is slightly higher than in the case with ABL inflow, while the thrust coefficients remains approximately the same. It is not clear whether the difference is due to the shear layer and/or increased turbulence or if it is a Reynolds number effect. The Reynolds numbers based on hub velocity and rotor diameter were ![]() for the NBL case and
for the NBL case and ![]() for the ABL case. A previous study by [9] showed a clear Reynolds number dependence in a similar range: an increase in Reynolds number from
for the ABL case. A previous study by [9] showed a clear Reynolds number dependence in a similar range: an increase in Reynolds number from ![]() to
to ![]() resulted in
resulted in
![]()
![]()
Figure 4. Inflow conditions: streamwise turbulence intensity for (a) the NBL case and (b) the ABL case.
an increase in ![]() with 12%. Included in Figure 5 is also computations using the BEM method. By looking at the BEM results for the NBL and ABL cases, it can be seen that this method predicts an increasing
with 12%. Included in Figure 5 is also computations using the BEM method. By looking at the BEM results for the NBL and ABL cases, it can be seen that this method predicts an increasing![]() , but an almost constant
, but an almost constant![]() , when increasing the Reynolds number, suggesting that the differences between the NBL and ABL cases are a Reynolds number effect. For both cases, the BEM computations predict a higher power output and a lower thrust as compared to the measurements. The discrepancies is due to the lack of measured airfoil data (lift and drag) for these low Reynolds numbers. The BEM computa- tions do however show the same trend as the measurements, for both
, when increasing the Reynolds number, suggesting that the differences between the NBL and ABL cases are a Reynolds number effect. For both cases, the BEM computations predict a higher power output and a lower thrust as compared to the measurements. The discrepancies is due to the lack of measured airfoil data (lift and drag) for these low Reynolds numbers. The BEM computa- tions do however show the same trend as the measurements, for both ![]() and
and![]() .
.
3.2. Wake Velocity Comparison between Hot-Film and PIV
In order to validate the PIV measurements, a few profiles were also measured with hot-film. An overall good agreement was found. In Figure 6, a comparison between hot-film measurements and PIV measurements is shown for the ABL case. The left column is the mean streamwise velocity and the right column is the corresponding turbulence intensity. The positions are ![]() downstream at three spanwise positions:
downstream at three spanwise positions:![]() ,
, ![]() and
and![]() . The reason for the larger discrepancy between hot-film and PIV in the mean velocity profiles at
. The reason for the larger discrepancy between hot-film and PIV in the mean velocity profiles at ![]() is most likely due to the fact that the wake deficit has a very sharp peak at
is most likely due to the fact that the wake deficit has a very sharp peak at![]() , due to the wake from the nacelle, which was already known from previous measurements [9] . A very small spanwise shift from the location of the maximum velocity deficit would therefore result in a larger velocity. From [9] , the sharp peak in velocity deficit can be estimated to
, due to the wake from the nacelle, which was already known from previous measurements [9] . A very small spanwise shift from the location of the maximum velocity deficit would therefore result in a larger velocity. From [9] , the sharp peak in velocity deficit can be estimated to ![]() over a spanwise distance
over a spanwise distance![]() . By only looking at the hot-film measurements, it can be seen that the peak in
. By only looking at the hot-film measurements, it can be seen that the peak in ![]() is moving towards the centreline as we move further out in the spanwise direction. It suggests that the turbine is producing a
is moving towards the centreline as we move further out in the spanwise direction. It suggests that the turbine is producing a
lot of turbulence on the edge of the rotor disc on the upper half side, but not on the lower half, which has also been seen in previous studies [4] [6] .
3.3. Wake Flow Comparison between NBL and ABL Inflow
Vertical profiles of mean streamwise (![]() ) and vertical (
) and vertical (![]() ) velocity in the wake are shown in Figures 7-9. The profiles correspond to the wake centerline
) velocity in the wake are shown in Figures 7-9. The profiles correspond to the wake centerline
location ![]() (Figure 7),
(Figure 7), ![]() (Figure 8) and
(Figure 8) and ![]() (Figure 9), res- pectively. Each figure shows a comparison between the NBL and the ABL cases for three different downstream positions:
(Figure 9), res- pectively. Each figure shows a comparison between the NBL and the ABL cases for three different downstream positions:![]() ,
, ![]() and
and![]() . Already
. Already
this close to the turbine, the ABL case shows a faster recovery of the wake with smoother profiles. This result is not surprising and is due to the higher inlet turbulence levels in the ABL case, which enhances the mixing and transport of momentum. For the vertical component, it can be seen that at ![]() and
and![]() , the NBL and ABL cases are similar, while a larger difference can be seen at
, the NBL and ABL cases are similar, while a larger difference can be seen at![]() . The largest values of
. The largest values of ![]() are seen at
are seen at![]() , where it reaches above 10% of the hub velocity. The measurements are taken at the negative spanwise side where a positive vertical component can be expected, assuming that the wake is rotating in the opposite direction as the rotor. Note, the rotor is rotating clockwise when looking in the streamwise direction.
, where it reaches above 10% of the hub velocity. The measurements are taken at the negative spanwise side where a positive vertical component can be expected, assuming that the wake is rotating in the opposite direction as the rotor. Note, the rotor is rotating clockwise when looking in the streamwise direction.
The corresponding profiles of streamwise (![]() ) and vertical (
) and vertical (![]() ) turbulence intensity are shown in Figures 10-12. In the streamwise component (left co- lumns of the figures), it can be seen that the turbine in general produces kinetic energy in the NBL case: the values of
) turbulence intensity are shown in Figures 10-12. In the streamwise component (left co- lumns of the figures), it can be seen that the turbine in general produces kinetic energy in the NBL case: the values of ![]() are in general higher after the tur- bine than at the inlet. In the ABL case on the other hand, the turbulence levels in the wake are of the same order as at the inlet, about 15% of
are in general higher after the tur- bine than at the inlet. In the ABL case on the other hand, the turbulence levels in the wake are of the same order as at the inlet, about 15% of![]() . Apparently, the turbine does not generate additional turbulence in this case. The tip vortices can clearly be seen as a peak in the turbulence levels in some of the positions for the NBL case, but not in the ABL case. This is particularly clear around
. Apparently, the turbine does not generate additional turbulence in this case. The tip vortices can clearly be seen as a peak in the turbulence levels in some of the positions for the NBL case, but not in the ABL case. This is particularly clear around
![]() at
at ![]() (Figure 11) and around
(Figure 11) and around ![]() at
at ![]() (Figure 12(a)). It is possible that the higher inlet turbulence levels in the ABL case make the tip vortices break down faster, which would explain why they are not detectable in these images.
(Figure 12(a)). It is possible that the higher inlet turbulence levels in the ABL case make the tip vortices break down faster, which would explain why they are not detectable in these images.
Large differences between the two cases can be seen in the vertical component of the turbulence intensity (right columns of Figures 10-12). The increased turbulence and shear of the ABL case changes the ![]() completely in the NBL case. The tip vortices are visible as sharp peaks in
completely in the NBL case. The tip vortices are visible as sharp peaks in ![]() at
at ![]() and
and![]() , but not in the ABL case. The mean vertical component
, but not in the ABL case. The mean vertical component ![]() at the inlet was below 0.5% of the streamwise velocity, in both the NBL and the ABL cases. The vertical component of the turbulence intensity
at the inlet was below 0.5% of the streamwise velocity, in both the NBL and the ABL cases. The vertical component of the turbulence intensity ![]() was 3% and 12% at the inlet, in the NBL and ABL cases, respectively. In the NBL case, the values of
was 3% and 12% at the inlet, in the NBL and ABL cases, respectively. In the NBL case, the values of ![]() in the wake is around 5% in average, meaning that the turbine increases
in the wake is around 5% in average, meaning that the turbine increases ![]() as compared to the inlet. For the ABL case,
as compared to the inlet. For the ABL case, ![]() remains in average about the same as at the inlet, about 12% in average, even though the distribution is changing.
remains in average about the same as at the inlet, about 12% in average, even though the distribution is changing. ![]() is here varying between 8% - 17%.
is here varying between 8% - 17%.
3.4. Visualization of the Tip Vortices
The clear peaks in turbulence intensity displayed in Figure 11(a) and Figure 11(b) correspond to the tip vortices. Instantaneous velocity images of streamwise and vertical velocity are shown at this location in Figure 13(a) and Figure 13(b), respectively. The tip vortices can be seen as adjacent regions of high and low speed. The result, based on both images, is a counter-clockwise rotation of the vortices. This is shown more clearly in Figure 14, where the local mean velocity ![]() has been subtracted from each point in Figure 13(a), in order to suppress the influence of the boundary layer. The arrows correspond to the vector sum of
has been subtracted from each point in Figure 13(a), in order to suppress the influence of the boundary layer. The arrows correspond to the vector sum of ![]() and
and![]() , which shows the actual additional rota- tion caused by the vortices.
, which shows the actual additional rota- tion caused by the vortices.
3.5. Vortex Statistics
In order to study the vortex statistics of this flow case, an in-house developed vortex detection program was used, which is described in [20] [21] . Vortices are
here detected by using the approach suggested by [22] , which is based on iden- tifying closed or spiral streamline patterns by looking at the complex eigenvalues of the 2D velocity gradient tensor:
![]() (5)
(5)
A vortex is then defined as a region where the imaginary eigenvalues ![]() are positive and greater than a predefined threshold value. The vortex strength is here defined as the maximum imaginary eigenvalue (
are positive and greater than a predefined threshold value. The vortex strength is here defined as the maximum imaginary eigenvalue (![]() ) within the identified region, and the position of
) within the identified region, and the position of ![]() is defined as the vortex centre. The circulation
is defined as the vortex centre. The circulation ![]() is calculated according to:
is calculated according to:
![]() (6)
(6)
where ![]() is a circle with origin at the vortex centre. By performing this inte- gration, stepping outwards from the vortex centre until the maximum circula- tion is reached, each vortex can be identified and approximated by a circle. The diameter of this circle
is a circle with origin at the vortex centre. By performing this inte- gration, stepping outwards from the vortex centre until the maximum circula- tion is reached, each vortex can be identified and approximated by a circle. The diameter of this circle ![]() will in the following be used as a measure of the vortex size.
will in the following be used as a measure of the vortex size.
Figure 15 shows the 5% strongest vortices for each ![]() -position. The (+)-signs denote vortices which have positive circulation and counter-clockwise rotation, while the (
-position. The (+)-signs denote vortices which have positive circulation and counter-clockwise rotation, while the (![]() ’)-signs show vortices with negative circulation and clock- wise rotation. The spanwise position is at
’)-signs show vortices with negative circulation and clock- wise rotation. The spanwise position is at![]() , where the tip vortices could be seen clearly (see Figure 13 and Figure 14). For the NBL case, the strongest vortices are located in a smaller vertical region and most of them are in the same (counter-clockwise) direction. These are apparently the tip vortices, which are not as visible in the ABL case, where the vortices show a larger spread in
, where the tip vortices could be seen clearly (see Figure 13 and Figure 14). For the NBL case, the strongest vortices are located in a smaller vertical region and most of them are in the same (counter-clockwise) direction. These are apparently the tip vortices, which are not as visible in the ABL case, where the vortices show a larger spread in ![]() -direction and also a more even distribution of rotational direction. This is in accordance with the results from the turbulence intensity profiles shown in Figure 11, which showed signs of the tip vortices for the NBL case, but not for the ABL case. It should also be noted that the 5% strongest vortices shown here are much stronger in the NBL case; the strongest 5% corresponds to
-direction and also a more even distribution of rotational direction. This is in accordance with the results from the turbulence intensity profiles shown in Figure 11, which showed signs of the tip vortices for the NBL case, but not for the ABL case. It should also be noted that the 5% strongest vortices shown here are much stronger in the NBL case; the strongest 5% corresponds to ![]() for the most upstream position (
for the most upstream position (![]() ). For the ABL case, the 5%-threshold is
). For the ABL case, the 5%-threshold is![]() . Figure 15 is assembled from three different PIV images (i.e. three different downstream positions), which is the explanation for the gaps without vortices seen most clearly for the NBL case at
. Figure 15 is assembled from three different PIV images (i.e. three different downstream positions), which is the explanation for the gaps without vortices seen most clearly for the NBL case at ![]() and 2.1.
and 2.1.
Figure 16 shows the 5% largest vortices for the NBL (upper figure) and ABL (lower figure) cases. It can again be seen that the vortices in the NBL case are spread over a smaller vertical distance and are to a larger extent in the same direction. The probability density function (PDF) of the vortex size for all
![]()
Figure 15. The 5% strongest vortices identified by the vortex detection program, for the NBL case (upper figure) and ABL case (lower figure). (+) denotes positive circulation and counter-clockwise rotation, while (![]() ) denotes negative circulation and clockwise rotation.
) denotes negative circulation and clockwise rotation.
detected vortices is shown in Figure 17(a) and Figure 17(b), for the NBL and ABL cases, respectively. The figure shows one function for every downstream image (three different downstream regions, corresponding to the three different PIV images that were taken).
For the NBL case, the vortices are decreasing in size with downstream dis- tance. In contrary, for the ABL case, the vortices have about the same size for all positions. The vortex diameter corresponding to the highest peak in the PDF for the NBL case is decreasing from about 0.10 to approximately 0.077, while it remains around 0.083 for all three positions in the ABL case. A possible ex- plaination is that different types of vortices are detected in the two cases. For the NBL case, mainly large, strong tip vortices are detected, which apparently de- crease in size as they are convected downstream. In the ABL case, the vortices are smaller (at least far upstream), weaker, appear in both directions and are spread over a larger vertical distance. These vortices do not decrease in size in the same way as the tip vortices.
![]()
Figure 16. The 5% largest vortices identified by the vortex detection program, for the NBL case (upper figure) and ABL case (lower figure). (+) denotes positive circulation and counter-clockwise rotation, while (![]() ) denotes negative circulation and clockwise rotation.
) denotes negative circulation and clockwise rotation.
![]()
![]()
Figure 17. Probability density function of the vortex diameter ![]() for three different down- stream regions. (a) NBL and (b) ABL.
for three different down- stream regions. (a) NBL and (b) ABL.
4. Summary and Conclusions
Velocity measurements were performed in the wake behind a small-scale model wind turbine placed in a wind tunnel. For validation purposes, both PIV and hot-film measurements were conducted, and an overall good agreement between the two techniques was found. Two flow cases were then compared, one with an inflow corresponding to a naturally developing boundary layer (NBL) and one to an atmospheric boundary layer (ABL) inflow, generated with triangular spires and roughness elements along the beginning of the test section. The NBL profile had an inlet turbulence level of 1.3% in the streamwise component while the ABL had 15%. Furthermore, the ABL profile had a strong shear across the rotor disc.
The power output was found to be slightly lower in the ABL case, due to either the increased shear and turbulence, or the lower Reynolds number, since this case had a somewhat lower hub velocity. The thrust coefficient remained about the same for both cases. Further studies are needed in order to fully explain the difference in the power output between the cases, it can however be concluded that the model behaves as expected, with a smooth power curve (power coefficient as a function of tip speed ratio), where the optimum power output was found at a tip speed ratio of 5, for which the blades were designed according to the blade element momentum method.
The focus of the study was the velocity and turbulence distributions in the near wake and the differences between the cases with different inlet conditions. It was seen that already before![]() , the larger turbulence level in the ABL case caused a more pronounced mixing and transport of momentum, which caused a faster recovery of the wake. For the same reason, the ABL velocity profiles were overall smoother compared to the NBL case. This was observed for both the streamwise and the vertical mean velocities, as well as the corresponding turbulence intensities. Larger differences between the cases were found for the streamwise velocity than for the vertical one. As expected, a rotation of the wake in the direction opposite to the rotational direction of the turbine rotor was found.
, the larger turbulence level in the ABL case caused a more pronounced mixing and transport of momentum, which caused a faster recovery of the wake. For the same reason, the ABL velocity profiles were overall smoother compared to the NBL case. This was observed for both the streamwise and the vertical mean velocities, as well as the corresponding turbulence intensities. Larger differences between the cases were found for the streamwise velocity than for the vertical one. As expected, a rotation of the wake in the direction opposite to the rotational direction of the turbine rotor was found.
By comparing the turbulence levels before and after the turbine (i.e. inlet and wake), one may conclude that both ![]() and
and ![]() in average had the same levels upstream and downstream of the turbine for the ABL case. The dis- tributions were however modified, even though the average levels remained similar. For the NBL case on the other hand, there was a significant increase of both
in average had the same levels upstream and downstream of the turbine for the ABL case. The dis- tributions were however modified, even though the average levels remained similar. For the NBL case on the other hand, there was a significant increase of both ![]() and
and ![]() in the wake, showing that the turbine acts more like a turbulence generator in this case, instead of only redistributing energy. For the NBL case, clear peaks could be seen in both
in the wake, showing that the turbine acts more like a turbulence generator in this case, instead of only redistributing energy. For the NBL case, clear peaks could be seen in both ![]() and
and ![]() where the tip vortices are expected to be found. No peaks were however visible in the ABL case, suggesting that the vortices likely break down earlier in this case, due to the higher turbulence at the inlet. These results were supported by an analysis performed with an in-house developed vortex detection program. This analysis showed clear signs of tip vortices for the NBL case, but not for the ABL case. The majority of the detected vortices for the NBL case were in the counter-clockwise direction, corresponding to the direction of the tip vortices. The vortices in the NBL case were also found to be stronger and spread over a smaller vertical distance as compared to the ABL case.
where the tip vortices are expected to be found. No peaks were however visible in the ABL case, suggesting that the vortices likely break down earlier in this case, due to the higher turbulence at the inlet. These results were supported by an analysis performed with an in-house developed vortex detection program. This analysis showed clear signs of tip vortices for the NBL case, but not for the ABL case. The majority of the detected vortices for the NBL case were in the counter-clockwise direction, corresponding to the direction of the tip vortices. The vortices in the NBL case were also found to be stronger and spread over a smaller vertical distance as compared to the ABL case.
Comparing the present distribution of ![]() in the wake with the turbulent kinetic energy distribution (based on streamwise and vertical components) measured in another, but similar study [5] , shows large discrepancies. Even though the latter study was conducted at another tip speed ratio and with another boundary layer inflow, the main reason for the discrepancies is that the flow in the near wake is heavily determined by the blade aerodynamics. The present study used a SD7003 airfoil, while [5] used a reversely mounted propeller blade (MA0530TE). The choice of airfoil will have a large effect on the near wake, both in terms of mean flow and turbulence levels, which complicates comparisons between different cases. This constitutes a major reason for performing more near wake measurements on different types of turbine models, in order to be able to draw general conclusions regarding the flow in the near wake.
in the wake with the turbulent kinetic energy distribution (based on streamwise and vertical components) measured in another, but similar study [5] , shows large discrepancies. Even though the latter study was conducted at another tip speed ratio and with another boundary layer inflow, the main reason for the discrepancies is that the flow in the near wake is heavily determined by the blade aerodynamics. The present study used a SD7003 airfoil, while [5] used a reversely mounted propeller blade (MA0530TE). The choice of airfoil will have a large effect on the near wake, both in terms of mean flow and turbulence levels, which complicates comparisons between different cases. This constitutes a major reason for performing more near wake measurements on different types of turbine models, in order to be able to draw general conclusions regarding the flow in the near wake.
The present paper presents velocity data from the near wake region behind a model wind turbine. Due to high turbulence and possible reflections from the model, it is a hard region to measure and study accurately. It is nevertheless an important region, since it will set the boundary conditions for the far wake, where additional turbines might be placed when building wind power farms. For a real wind power farm, the inlet conditions usually vary and it is therefore important to know how the inlet conditions affect the wake behaviour. Increased knowledge can be gained by comparing different cases in a wind tunnel, even though the extrapolation to larger scales is not trivial. There is a need for more experimental data in this area to be able to draw general conclusions, in par- ticular with respect to possible upscaling effects. The data in this study can in the future also be used for validation of numerical models.
Acknowledgements
The head of the laboratory at University of Gävle, Leif Claesson, is gratefully acknowledged for assistance with the wind tunnel, the hot-film anemometry and the setup of the atmospheric boundary layer. Dr. Bengt Fallenius is gratefully acknowledged for assistance with the vortex detection program.