1. Introduction
Given a positive matrix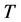 , in 1968 Gustafson proved
, in 1968 Gustafson proved
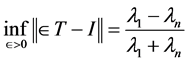 (1)
(1)
where
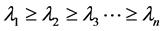 (2)
(2)
are eigenvalues of 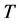 such that
such that 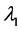 and
and 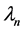 are the largest and the smallest eigenvalues of
are the largest and the smallest eigenvalues of 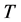 respectively. Please see [1] [2] [3] .
respectively. Please see [1] [2] [3] .
The equality (1) played an important role in establishing what Gustafson calls “operator trigonometry”. In fact, for a positive matrix 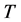 he defined
he defined 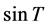 to be
to be
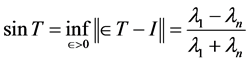 (3)
(3)
He proved (1) by using the convexity of the Hilbert space norm and other Hilbert space properties.
Later, in his investigation on problems of antieigenvalue theory, this author discovered a useful lemma which he calls the Two Nonzero Component Lemma or TNCL, for short (see [4] [5] [6] ). The antieigenvalue of an accretive operator 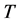 acting on a complex Hilbert space is defined to be
acting on a complex Hilbert space is defined to be
 (4)
(4)
For positive matrices, there is a relationship between the antieigenvalue of 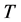 and
and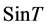 . In a series of papers this author applied his TNCL to compute antieigenvalues of different types of operators, including normal operators. He also applied TNCL to compute other types of antieigenvalue quantities such as total antieigenvalues, higher order antieigenvalues,and joint antieigenvalues. Furthermore, he applied TNCL to solve some optimization problems in statistics, econometrics, and resource allocations. Please see [5] - [11] . Although this Lemma is implicitly used in all of the author's earlier papers up to 2008, it was not until 2008 that he stated a formal description of the Lemma in his paper titled, “Antieigenvalue Techniques in Statistics.” Below is the statement of the lemma. For an early proof of the lemma please see the author’s work in [5] .
. In a series of papers this author applied his TNCL to compute antieigenvalues of different types of operators, including normal operators. He also applied TNCL to compute other types of antieigenvalue quantities such as total antieigenvalues, higher order antieigenvalues,and joint antieigenvalues. Furthermore, he applied TNCL to solve some optimization problems in statistics, econometrics, and resource allocations. Please see [5] - [11] . Although this Lemma is implicitly used in all of the author's earlier papers up to 2008, it was not until 2008 that he stated a formal description of the Lemma in his paper titled, “Antieigenvalue Techniques in Statistics.” Below is the statement of the lemma. For an early proof of the lemma please see the author’s work in [5] .
Lemma 1 (The Two Nonzero Component Lemma) Let 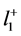 be the set of all sequences with nonnegative terms in the Banach Space
be the set of all sequences with nonnegative terms in the Banach Space . That is, let
. That is, let
 (5)
(5)
Let
 (6)
(6)
be a function from ![]() to
to![]() . Assume
. Assume ![]() for
for![]() ,
, ![]() , and
, and![]() . Then the minimizing vectors for the function
. Then the minimizing vectors for the function
![]() (7)
(7)
on the convex set ![]() have at most two nonzero components.
have at most two nonzero components.
What make the proof of the Lemma possible are the following two facts: First, the convexity of the set
![]() (8)
(8)
Second, a special property that the functions
![]() (9)
(9)
involved possess. If we set
![]() (10)
(10)
then all restrictions of the form
![]() (11)
(11)
of
![]() (12)
(12)
have the same algebraic form as ![]() itself. For example if
itself. For example if
![]() (13)
(13)
then we have
![]() (14)
(14)
which has the same algebraic form as
![]() (15)
(15)
Indeed, for any![]() ,
,![]() ; all restrictions of the function
; all restrictions of the function
![]() (16)
(16)
obtained by setting an arbitrary set of ![]() components of
components of ![]() equal to zeros have the same algebraic form as
equal to zeros have the same algebraic form as![]() . Obviously, not all functions have this property. For instance, for the function
. Obviously, not all functions have this property. For instance, for the function![]() ,
, ![]() , which does not have the same algebraic form as
, which does not have the same algebraic form as![]() .
.
In the next section we prove that Gustafson’s identity (1) can be obtained using this author’s the Two Nonzero Component Lemma or TNCL. Our proof is elementary (comparing to Gustafson’s proof) in the sense that we use only TNCL and techniques of calculus.
2. A Proof of (1) Based on TNCL
Theorem 2 Let ![]() be a positive matrix where
be a positive matrix where
![]()
are eigenvalues of ![]() such that
such that ![]() and
and ![]() are the largest and the smallest eigenvalues of
are the largest and the smallest eigenvalues of![]() , then
, then
![]() (17)
(17)
Proof. Note that if we square the left hand side of (17) we get
![]() (18)
(18)
Thus, we need to show
![]() (19)
(19)
Now to follow notations usually used in differential calculus, let’s substitute ![]() with
with ![]() and consider
and consider
![]() (20)
(20)
instead. With this change of notation. now we apply spectral theorem to the positive matrix ![]() and assume
and assume
![]()
are components of ![]() with respect to an orthogonal basis corresponding to
with respect to an orthogonal basis corresponding to
![]()
Therefore, we can rewrite (20) as
![]() (21)
(21)
Applying TNCL we can assume any optimizing vector
![]()
is so that only two of its components, say ![]() and
and ![]() are nonzero and the rest of them are zero. Keeping that in mind, for such optimizing vectors
are nonzero and the rest of them are zero. Keeping that in mind, for such optimizing vectors ![]() (21) will be reduced to
(21) will be reduced to
![]() (22)
(22)
To compute (22), let’s do some change of variables first. Substitute ![]() for
for![]() ,
, ![]() for
for![]() , and
, and ![]() for
for![]() . (22) then becomes
. (22) then becomes
![]() (23)
(23)
For a fixed ![]() we compute the
we compute the ![]() in (23) with respect to
in (23) with respect to ![]() first. Consider the expression
first. Consider the expression
![]() (24)
(24)
We next find the derivative of (24) with respect to ![]() and set it equal to zero
and set it equal to zero
![]() (25)
(25)
and then solve it for![]() . The solution is
. The solution is
![]() (26)
(26)
Assume ![]() and note that the second derivative of (24) is
and note that the second derivative of (24) is
![]() (27)
(27)
which is positive. This shows
![]() (28)
(28)
is indeed a minimizing value. If we substitute ![]() from (26) in 24) and simplify we get
from (26) in 24) and simplify we get
![]() (29)
(29)
The derivative of (29) with respect to ![]() is
is
![]() (30)
(30)
To find the optimizing value![]() , we solve the following equation with respect to
, we solve the following equation with respect to![]() .
.
![]() (31)
(31)
The solution of (31) is
![]() (32)
(32)
If we substitute the value of ![]() from (32) in (29) and simplify we get
from (32) in (29) and simplify we get
![]() (33)
(33)
The second derivative of (29) is
![]() (34)
(34)
which is negative, under our assumption that![]() . This indicates that
. This indicates that ![]() given by (32) is indeed a maximizing vector. Thus we have proved
given by (32) is indeed a maximizing vector. Thus we have proved
![]() (35)
(35)
Finally, we show that ![]() and
and![]() . To show this note that
. To show this note that
![]() (36)
(36)
Now define
![]() (37)
(37)
and notice that
![]() (38)
(38)
Hence ![]() is decreasing and
is decreasing and ![]() has the largest value when
has the largest value when ![]() takes the smallest value. That is when
takes the smallest value. That is when ![]() and
and![]() .
.
Remark 3 The equality (35) is valid even if ![]() is an infinite dimensional positive operator acting on a separable Hilbert space. The reason is that TNCL is valid both when
is an infinite dimensional positive operator acting on a separable Hilbert space. The reason is that TNCL is valid both when ![]() has a finite or infinite number of components. However, in the case of an infinite dimensional positive operator, we do not know for what pair of
has a finite or infinite number of components. However, in the case of an infinite dimensional positive operator, we do not know for what pair of ![]() and
and ![]() (35) holds.
(35) holds.
3. Conclusion
We showed that TNCL can be used to prove an identity which was proved by Karl Gustafson in 1968. This identity was part of his min-max theorem. The identity was the basis of operator trigonometry. The original proof was based on Hilbert space techniques and convexity of operator norm. Using TNCM we reduced the problem to a very simple problem in elementary calculus. This indeed shows the power of this dimension reducing optimization lemma which is used by this author in many of his previous work. The lemma not only proved equality (1) but, as we noted in the remark above, it extended it to the case of positive operators on an infinite dimensional Hilbert space.
Acknowledgement
The author wishes to thank the referee of this paper for his helpful suggestions.