Generation and Detection of a Directed Monoenergetic Neutrino Beam with Hydrogen-Like Ions

Lorcan Michael Folan, Vladimir I. Tsifrinovich

Department of Applied Physics, NYU Tandon School of Engineering, Brooklyn, NY, USA.

DOI: 10.4236/wjnst.2017.71005                

Abstract

We consider two possible schemes for generation and detection of a monoenergetic directed beam of neutrinos which may have application to neutrino communication. First, we consider generation of a directed neutrino beam using electron capture beta decay in hydrogen-like ions. Next, we suggest detection of a directed neutrino beam using resonant absorption of a neutrino by a bare nucleus with the generation of a bound electron. This reaction is inverse to electron capture beta decay, and we call it “Bound State Inverse Beta Decay (BSIBD)”. We show that the recoil effect can be eliminated by an appropriate choice of velocities for the ions and bare nuclei. Finally, we consider a combination of a solid state source of a directed mono-energetic neutrino beam and its detection using BSIBD.

Keywords

Neutrino Communication, Directed Neutrino Beam, Electron Capture Beta Decay, Hydrogen-Like Ions

1. Introduction

Reliable generation and detection of neutrinos could open the way for direct communication between any two points in space and on the Earth, including underground and underwater locations. Recently, communication with a modulated neutrino beam was demonstrated using the NuMI beam line and the MINERvA detector at Fermilab [1] . An important task is the development of alternative schemes of neutrino communication which could be more practical and economical for applications. In this paper, we consider two schemes exploiting directed monoenergetic neutrino beams and hydrogen-like ions.

It was shown recently that using a Gamow-Teller transition in electron capture beta-decay one can generate a directed monoenergetic neutrino beam if the temperature of a radioactive source is small compared to the energy separation between the lowest Zeeman energy levels for a sample in a strong magnetic field [2] [3] . The most favorable solid state source is a ferromagnet with a strong hyperfine interaction between the electron and nuclear spins. The temperature required for the generation of the directed beam is rather low: in the most favorable case of antimony ¹¹⁹Sn, reported in [2] , the separation between the lowest energy levels is about 36 mK (the corresponding hyperfine field on the antimony nuclei is 70.6 T). The directed neutrino beam can be switched and modulated by manipulation of the magnitude and direction of the magnetic field. It was also shown that electron capture beta-decay in hydrogen-like ions is extremely sensitive to the hyperfine interaction [4] [5] [6] [7] [8] . In fact, the decay from one of the hyperfine states can be completely forbidden. This feature can also be used for switching and modulation of radioactive decay and neutrino radiation.

Directed neutrino beams derived from radioactive sources rather than accelerators also have potential applications in other neutrino experiments. Unconventional detection schemes have been suggested for direct detection of cosmic neutrino background using neutrino capture by beta-decaying nuclei, e.g. tritium. This proposal utilizes the change in the maximum kinetic energy of electrons generated by neutrino capture compared those from a beta-decay [9] [10] . Another proposal is to use cold Rydberg atoms to measure the electron neutrino mass [11] . In [11] , the authors consider beta decay of cold atomic tritium. They suggest measurement of the momenta of the daughter helium ions and the electrons. The electrons pass through an optical lattice of cold rubidium atoms which are prepared in a high Rydberg state, e.g. the 53 S state. Passing electrons drive the rubidium atoms into the 53 P state. The atoms in the 53 P state are then ionized, and the detected rubidium ions reveal the momentum of the passing electrons. Monoenergetic, directional neutrino sources and novel detection schemes thus have potentially wide application.

In Section 2 of this paper, we consider the generation of a directed monoen- ergetic neutrino beam using hydrogen-like ions. We show the opportunity to relax the requirement for the very low temperature in the generation of the directed neutrino beam. In Section 3, we suggest the resonant detection of the neutrino beam using BSIBD and show that effects of recoil can be eliminated. Finally, in Section 4 we discuss the combination of a solid state source of a directed neutrino beam and its detection with BSIBD.

2. Generation of a Directed Neutrino Beam

For definiteness, we will consider a hydrogen-like ion with a nuclear spin.

(Generalization to an arbitrary spin will be obvious). Let the nucleus of a hydrogen-like ion with atomic number capture the K (1 S) electron and decay into

a nucleus with atomic number 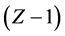and nuclear spin radiating an

electron neutrino (see Figure 1). We will assume that the ion is placed in a

Figure 1. Illustration of K electron capture beta-decay in a hydrogen-like ion, with a decrease of nuclear spin by one unit.

uniform magnetic field, which points in the positive z-direction, and the hyperfine splitting is much greater than the Zeeman splitting.

With no magnetic field we have two hyperfine levels corresponding to the two

values of the total angular momentum. Typically, the hyperfine con-

stant and the nuclear magnetic moment are positive. In this case the lower “−” sign corresponds to the lower hyperfine level, and the upper “+” sign corresponds to the upper level. An accurate expression for the hyperfine splitting in a hydrogen-like ion can be found in [12] . For an estimate, one can use the approximate formula

(1)

Here, and are the electron and proton masses, is the fine

structure constant, is the nuclear magnetic moment, and is the nuclear magneton. As an example, for a hydrogen-like ion of the isotope, which decays through electron capture to the stable isotope, the hyperfine splitting. The splitting is large due to the Z³ dependence.

An external magnetic field splits a hyperfine level with total angular momentum F into levels. The energy splitting in a magnetic field B can be estimated using the Breit-Rabi formula [13] .

(2)

Here, energy is measured from the midpoint between the hyperfine levels at

,. A typical scheme of the energy levels for

is shown in Figure 2. Note that the electron capture beta decay from the levels is forbidden by the conservation of the z-component of the total angular

momentum, which for a nucleus of spin and a neutrino cannot be greater

than 2. (The levels can be used to switch the nuclear decay on and off).

If the hydrogen-like ion is initially in the lowest level, then after the

decay, the neutrino must have spin “up” in order to conserve the

z-component of the total angular momentum. Due to the helicity requirement the neutrino must propagate in the negative z-direction as a directed beam (see Figure 3(a)).

The first term in parentheses in Equation (2) is small compared to the second one as. Thus, the energy separation between the lowest two energy

levels for can be estimated as

(3)

It follows that the energy separation between the lowest energy levels in a hydrogen-like ion can be much greater than that in a ferromagnetic sample. As an

Figure 2. Hyperfine and Zeeman energy levels of a hydrogen-like ion with nuclear spin 5/2 in an external magnetic field. The hyperfine interaction produces the large splitting between the F = 2 and F = 3 states while the Zeeman splitting due to the external magnetic field breaks the degeneracy of the F_z levels.

(a)(b)

Figure 3. (a) Directional neutrino radiation from the lowest energy level. To conserve the z-component of the total angular momentum of the atomic system, the neutrino must be emitted in negative z direction. (b) Resonant detection of directed neutrino radiation using BSIBD, the reaction inverse to electron capture beta decay. For the neutrino to be captured and a bound K shell electron generated in the daughter atom, the electron must be produced resonantly in the state.

example, for in a field, the energy splitting, which is much greater than the value found in [2] .

3. Detection of Neutrinos Using BSIBD

In this section we describe BSIBD, a process which is inverse to electron capture beta decay and can be used for detection of neutrinos. Consider the reaction between a bare nucleus of atomic number and a neutrino as shown in Figure 3(b):

(4)

With a directed monoenergetic neutrino beam and an external magnetic field this process becomes a resonant one: the neutrino energy can be “tuned” to the energy difference between the corresponding states of the initially bare nucleus and the final hydrogen-like ion. Assume that the external magnetic field points in the positive z-direction, and the neutrino propagates in the negative z-direction as shown in Figure 3(b). In the lowest energy level the spin of the bare nucleus points “up”. A nucleus with atomic number and spin

captures a neutrino and transforms into a nucleus with the atomic number and spin, generating a K electron with spin component. The z-component of the total angular momentum does not change. Note that the state with and (i.e. in

Figure 2) also satisfies conservation of the z-component of the angular momentum but its energy is much higher. A newborn hydrogen-like ion can be detected by separation of the nucleus and the electron or using spectroscopic methods.

So far we ignored the effects of recoil, which could ruin our proposal for resonant BSIBD. Below we will show that the recoil effect can be eliminated. Consider again an electron capture beta decay. Let the hydrogen-like ions move in the negative z-direction with a uniform speed, where index “1” will refer to the hydrogen-like ions, and index “2” to the bare nuclei (see Figure 4(a), where “up” corresponds to the positive z-direction). After the decay the bare daughter nuclei move with the speed. Let be the rest energy of a hydrogen- like ion and be the rest energy of a bare daughter nucleus.

The basic idea is the following. We suggest choosing the speed of the hydrogen-like ions such that after the decay the bare nucleus will move in the opposite direction with kinetic energy equal to the kinetic energy of the hydrogen-like ion (see Figure 4(a)). In this case from energy conservation

(5)

(a)(b)

Figure 4. To enable resonant detection of a neutrino, the momenta of the constituents should be matched. (a) In an electron capture beta decay the kinetic energy of the bare daughter nucleus equals the kinetic energy of the hydrogen-like ion. (b) In BSIBD the kinetic energy of the hydrogen-like ion equals the kinetic energy of the bare nucleus which absorbed the neutrino.

Here, is the neutrino energy, is the neutrino momentum. Thus, the neutrino energy is

(6)

and the recoil effect is eliminated. Equating the kinetic energies of the hydrogen-like ion and the bare nucleus, and using the conservation of momentum

(7)

we obtain the formula for the speed of the hydrogen-like ions before the decay

(8)

(The “−” sign in Equation (7) corresponds to motion in the negative z-direction).

A similar analysis can be performed for BSIBD (see Figure 4(b)). We assume that a bare nucleus with atomic number moves in the positive z-dire- ction (upward in Figure 4(b)) with kinetic energy. After the absorption of a neutrino, which moved in the negative z-direction, the bare nucleus transforms to the hydrogen-like ion, which moves in the negative z- direction with kinetic energy. In this case we have the equations

(9)

Solving these equations we see that the speed of the bare nucleus before the absorption of a neutrino is given by the right hand side of Equation (8).

As an example, consider the electron capture beta decay of a cesium hydrogen-like ion to a stable xenon isotope

(10)

and the inverse process BSIBD

(11)

For these reactions, using Equation (8) we obtain an estimate of 390 m/s for the speed of the cesium hydrogen-like ion before generation of the neutrino and of the bare xenon nucleus before absorption of the neutrino.

Finally, we will estimate the detection rate in BSIBD. Assume that a nucleus in a hydrogen-like ion (the source) with the half-life capture its electron and emits a neutrino. The corresponding bare nucleus (the target) may capture the emitted neutrino and generate an electron in the K shell. The Bohr radius of

a hydrogen-like ion is. The simple argument given below helps one

to estimate the probability of neutrino capture. The electron in the hydrogen-like ion resides at a distance from the nucleus. During the time interval the electron is captured with probability close to one. We expect that in the inverse process BSIBD the neutrino residing near the bare nucleus during the time interval would also be captured with the probability close to 1. However, the neutrino propagates with the speed of light and passes through the region in the much smaller time interval. Thus, the probability of neutrino capture can be estimated as

. (12)

Now consider, for simplicity, a source in the shape of a rectangular prism, with square base of side. The source contains hydrogen-like ions. The ions are placed along linear chains and radiate neutrinos along those chains perpendicular to the base of the prism. The number of chains is, so that the number of ions in each chain is. During the time interval the number of emitted neutrinos is about. The neutrino flux can be estimated as

(13)

Next, consider a target, also in the shape of a rectangular prism with the same square base of side. The target contains bare nuclei which may capture neutrinos in BSIBD. Assume, for simplicity, that the bare nuclei are placed along the lines of propagation of neutrinos emitted by the source (the number of chains in the target is the same as in the source). During the time interval, the number of neutrinos captured by the bare nuclei is about. Thus, the expected detection rate can be estimated as

(14)

As an example, we will put, , and find how many hydrogen-like ions with the isotope and bare xenon nuclei are required for the unit detection rate 1/s. Using the methods developed in [2] and [4] , we estimate the half-life of a cesium hydrogen-like ion in the ground state to be about 26 days. Using this value we obtain, and

(15)

The corresponding mass of the target and the source is about 87 mg. Taking, for example, we obtain from Equation (13) the estimation for the corresponding neutrino flux:.

4. Solid State Source of Neutrino Radiation and BSIBD Detection

Finally, we will briefly discuss the combination of a solid state source of a directed monoenergetic neutrino beam and its detection using BSIBD. As an example, let us consider a ferromagnetic sample enriched with. (The hyperfine field on the cesium nuclei can be as large as 27.3 T [14] ). At millikelvin temperatures the isotope captures a K electron and radiates a directed beam of 320 keV neutrinos. If the neutrinos propagate in the negative z-direction (down-

ward in Figure 3(a)), the neutrino spin. Again, the neutrino beam can

be detected with bare nuclei. In a magnetic field pointing in the positive

z-direction, the lowest Zeeman state of this isotope has the nuclear spin.

The xenon nuclei absorb neutrinos and transmute into nuclei generating

an electron in the K shell as shown in Figure 3(b). In order

for detection to be possible the energy of neutrinos must be “tuned” to the energy difference between the corresponding states of the bare nucleus and the hydrogen-like ion. This can be done by adjusting the velocity of the bare nuclei.

5. Conclusion

We have suggested two neutrino emission and detection schemes, which could be used for neutrino communication. In both schemes a directed neutrino beam is detected by the bare nuclei using a resonant process, BSIBD, which is inverse to the electron capture beta decay. In the first scheme, the directed neutrino beam is generated by hydrogen-like ions. We have shown that the velocity of the hydrogen-like ions, which generate the neutrinos, can be chosen in such a way that the kinetic energy of the hydrogen-like ions before the emission of the neutrinos equals the kinetic energy of the bare nuclei after the emission. A similar result is obtained for bare nuclei which absorb neutrinos. In this case, the recoil effect does not affect the neutrino energy and does not prevent the absorption of the neutrino. The other scheme involves a solid state source of a directed neutrino beam.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Stancil D.D., et al. (2012) Demonstration of Communication Using Neutrinos. Modern Physics Letters A, 27, 1250077, 10 p. https://doi.org/10.1142/S0217732312500770
[2]	DeAngelis, C., Folan, L.M. and Tsifrinovich, V.I. (2012) Generation and Monitoring of Directed Neutrino Beams Using Electron-Capture Beta-Decay Sources. Physical Review C, 86, 034615, 4 p.
[3]	Folan, L.M. and Tsifrinovich, V.I. (2014) Generation of a Directed Mono-Energetic Neutrino Beam and Measurement of the Neutrino Mass. Modern Physics Letters A, 29, 1430042, 17 p.
[4]	Folan, L.M. and Tsifrinovich, V.I. (1995) Effects of the Hyperfine Interaction on Orbital Electron Capture. Physical Review Letters, 74, 499-501. https://doi.org/10.1103/PhysRevLett.74.499
[5]	Litvinov, Yu.A., et al. (2007) Measurement of the β+ and Orbital Electron-Capture Decay Rates in Fully Ionized, Hydrogenlike, and Heliumlike 140Pr Ions. Physical Review Letters, 97, 262501, 4 p.
[6]	Ivanov, A.N., Faber, M., Reda, R. and Kienle, P. (2008) Weak Decays of H-Like 140Pr58+ and He-Like 140Pr57+ Ions. Physical Review C, 78, 025503, 4 p.
[7]	Goni, M.A. (2010) Hyperfine Effects in Ionic Orbital Electron Capture. arXiv:1003.0583v1, 1-9.
[8]	Barabanov, A.L. and Titov, O.A. (2015) Electromagnetic Modulation of Monochromatic Neutrino Beams. European Physics Journal A, 51, 96-102.
[9]	Weinberg, S. (1962) Universal Neutrino Degeneracy. Physical Review, 128, 1457-1473. https://doi.org/10.1103/PhysRev.128.1457
[10]	Yanagisawa, C. (2014) Looking for Cosmic Neutrino Background. Frontiers in Physics, 2, 30-35.
[11]	Jerkins, M., et al. (2010) Using Cold Atoms to Measure Neutrino Mass. New Journal of Physics, 12, 043022, 9 p.
[12]	Shabaev, V.M., Shabaeva, M.B. and Tupitsyn, I.I. (1995) Hyperfine Structure of Hydrogenlike and Lithiumlike Atoms. Physical Review A, 52, 3686-3690. https://doi.org/10.1103/PhysRevA.52.3686
[13]	Bethe, H.A. and Salpeter, E.E. (1957) Quantum Mechanics of One and Two Electron Atoms. Springer, Berlin. https://doi.org/10.1007/978-3-662-12869-5
[14]	de Waard, H. and Reintsema, S.R. (1969) The Magnetic Hyperfine Field of Cesium in Iron Is Positive. Physics Letters A, 29, 290-291. https://doi.org/10.1016/0375-9601(69)90128-5