Padé Approximant for the Equation of Motion of a Supernova Remnant ()
1. Introduction
The equation of motion for a supernova remnant (SNR) can be modeled by a single law of motion or multiple laws of motion when the appropriate boundary conditions are provided. Examples of a single law of motion are: The Sedov expansion in the presence of a circumstellar medium (CSM) with constant density where the radius, r, scales as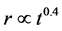 , see [1] , and the momentum conservation in the framework of the thin layer approximation with CSM at constant density where
, see [1] , and the momentum conservation in the framework of the thin layer approximation with CSM at constant density where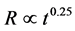 , see [2] . Examples of piece-wise solutions for an SNR can be found in [3] : A first energy conserving phase,
, see [2] . Examples of piece-wise solutions for an SNR can be found in [3] : A first energy conserving phase, 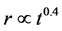 followed by a second adiabatic phase where
followed by a second adiabatic phase where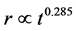 . At the same time it has been shown that in the first ten years of SN 1993J 1993j
. At the same time it has been shown that in the first ten years of SN 1993J 1993j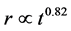 , which means an observed exponent larger than the previously suggested exponents, see [4] . The previ- ous analysis allows posing a basic question: “Is it possible to find an analytical solution for SNRs given the three observable astronomical parameters, age, radius and velocity ?”. In order to answer the above question, Section 2 introduces three profiles for the CSM, Section 3 derives three Padé approximated laws of motion for SNRs, and Section 4 closes the derived equations of motion for four SNRs.
, which means an observed exponent larger than the previously suggested exponents, see [4] . The previ- ous analysis allows posing a basic question: “Is it possible to find an analytical solution for SNRs given the three observable astronomical parameters, age, radius and velocity ?”. In order to answer the above question, Section 2 introduces three profiles for the CSM, Section 3 derives three Padé approximated laws of motion for SNRs, and Section 4 closes the derived equations of motion for four SNRs.
2. Profiles of Density
This section introduces three density profiles for the CSM: An exponential profile, a Gaussian profile, and a self-gravitating profile of Lane-Emden type.
2.1. The Exponential Profile
This density is assumed to have the following exponential dependence on r in spherical coordinates:
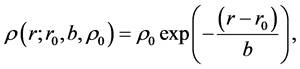 (1)
(1)
where b represents the scale. The piece-wise density is
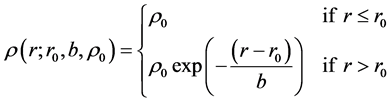 (2)
(2)
The total mass swept,  , in the interval
, in the interval 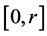 is
is
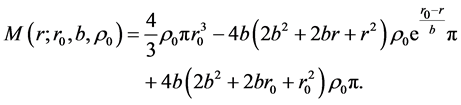 (3)
(3)
2.2. The Gaussian Profile
This density has the Gaussian dependence
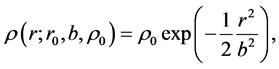 (4)
(4)
and the piece-wise density is
 (5)
(5)
The total mass swept,  , in the interval
, in the interval 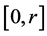 is
is
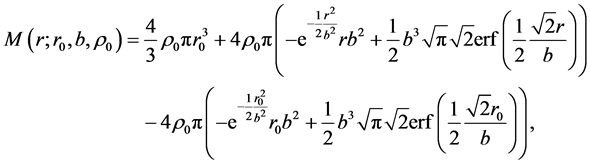 (6)
(6)
where 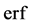 is the error function, see [5] .
is the error function, see [5] .
2.3. The Lane-Emden Profile
The Lane-Emden profile when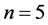 , after [6] [7] , is
, after [6] [7] , is
![]() (7)
(7)
![]() (8)
(8)
The total mass swept, ![]() , in the interval
, in the interval ![]() is
is
![]() (9)
(9)
3. The Equation of Motion
The conservation of the momentum in spherical coordinates in the framework of the thin layer approximation states that
![]() (10)
(10)
where ![]() and
and ![]() are the masses swept at
are the masses swept at ![]() and r, and
and r, and ![]() and v are the velocities of the thin layer at
and v are the velocities of the thin layer at ![]() and r.
and r.
3.1. Motion with Exponential Profile
Assuming an exponential profile as given by Equation (2) the velocity is
![]() (11)
(11)
where
![]()
and
![]()
In the above differential equation of the first order in r, the variables can be separated and integration gives the following non-linear equation:
![]() (12)
(12)
In this case is not possible to find an analytical solution for the radius, r, as a function of time. We therefore apply the Padé rational polynomial approximation of degree 2 in the numerator and degree 1 in the denominator about the point ![]() to the left-hand side of Equation (12):
to the left-hand side of Equation (12):
![]() (13)
(13)
The resulting Padé approximant for the radius ![]() is
is
![]() (14)
(14)
and the velocity is
![]() (15)
(15)
![]() (16)
(16)
and
![]() (17)
(17)
3.2. Motion with Gaussian Profile
Assuming a Gaussian profile as given by Equation (4) the velocity is
![]() (18)
(18)
where
![]() (19)
(19)
and
![]() (20)
(20)
The appropriate non-linear equation is
![]() (21)
(21)
The Padé rational polynomial approximation of degree 2 in the numerator and degree 1 in the denominator about ![]() for the left-hand side of the above equation gives
for the left-hand side of the above equation gives
![]() (22)
(22)
The resulting Padé approximant for the radius ![]() is
is
![]() (23)
(23)
and the velocity is
![]() (24)
(24)
![]() (25)
(25)
and
![]() (26)
(26)
3.3. Motion with the Lane-Emden Profile
Assuming a Lane-Emden profile, ![]() , as given by Equation (7), the velocity is
, as given by Equation (7), the velocity is
![]() (27)
(27)
where
![]() (28)
(28)
and
![]() (29)
(29)
The connected non-linear equation is
![]()
The Padé rational polynomial approximation of degree 2 in the numerator and degree 1 in the denominator for the left-hand side of the above equation gives
![]() (30)
(30)
where
![]() (31)
(31)
The Padé approximant for the radius is
![]() (32)
(32)
where
![]() (33)
(33)
and
![]() (34)
(34)
and the velocity is
![]() (35)
(35)
where
![]() (36)
(36)
and
![]() (37)
(37)
4. Astrophysical Applications
In the previous section, we derived three equations of motion in the form of non-linear equations and three Padé approximated equations of motion. We now check the reliability of the numerical and approximated solutions on four SNRs: Tycho, see [8] , Cas A, see [9] , Cygnus loop, see [10] , and SN 1006, see [11] . The three astronomical measurable parameters are the time since the explosion in years, t, the actual observed radius in pc, r, and the present velocity of expansion in km∙s−1, see Table 1. The astrophysical units have not yet been specified: pc for length and yr for time are the units most commonly used by astronomers. With these units, the initial velocity is![]() . The determination of the four unknown parameters, which are
. The determination of the four unknown parameters, which are![]() ,
, ![]() ,
, ![]() and b, can be obtained by equating the observed astronomical velocities and radius with those obtained with the Padé rational polynomial, i.e.
and b, can be obtained by equating the observed astronomical velocities and radius with those obtained with the Padé rational polynomial, i.e.
![]() (38)
(38)
![]() (39)
(39)
In order to reduce the unknown parameters from four to two, we fix ![]() and
and![]() . The two parameters
. The two parameters ![]() and
and ![]() are found by solving the two non-linear Equations (38) and (39). The results for the three types of profiles here adopted are reported in Tables 2-4.
are found by solving the two non-linear Equations (38) and (39). The results for the three types of profiles here adopted are reported in Tables 2-4.
![]()
Table 1. Observed astronomical parameters of SNRs.
![]()
Table 2. Theoretical parameters of SNRs for the padé approximated equation of motion with an exponential profile.
![]()
Table 3. Theoretical parameters of SNRs for the Padé approximated equation of motion with a gaussian profile.
![]()
Table 4. Theoretical parameters of SNRs for the Padé approximated equation of motion with a Lane-Emden profile.
The goodness of the approximation is evaluated through the percentage error, ![]() , which is
, which is
![]() (40)
(40)
where ![]() is the Padé approximated radius and
is the Padé approximated radius and ![]() is the exact solution which is obtained by solving numerically the non-linear equation of motion, as an example Equation (12) in the exponential case. The numerical values of
is the exact solution which is obtained by solving numerically the non-linear equation of motion, as an example Equation (12) in the exponential case. The numerical values of ![]() are reported in column 6 of Tables 2-4. Another useful astrophysical variable is the predicted decrease in velocity on the basis of the Padé approximated velocity,
are reported in column 6 of Tables 2-4. Another useful astrophysical variable is the predicted decrease in velocity on the basis of the Padé approximated velocity, ![]() , in 10 years, see column 7 of Tables 2-4.
, in 10 years, see column 7 of Tables 2-4.
5. Conclusion
The expansion of an SNR can be modeled by the conservation of momentum in the presence of a decreasing density: here we analysed an exponential, a Gaussian and a Lane-Emden profile. The three equations of motion have complicated left-hand sides but simple left-hand sides, viz.,![]() . The application of the Padé approximant to the left-hand side of the complicated equation of motion allows finding three appro- ximate laws of motion, see Equations (14, 23, 32), and three approximate velocities, see Equations (15, 24, 35). The astrophysical test is performed on four spherical SNRs assumed to be spherical and the four sets of parameters are reported in Tables 2-4. The percentage of error of the Padé approximated solutions for the radius is always less than 10% with respect to the numerical exact solution, see column 6 of the three last tables. In order to produce an astrophysical prediction, the theoretical decrease in velocity for the four SNRs here analysed is evaluated, see column 7 of Tables 2-4.
. The application of the Padé approximant to the left-hand side of the complicated equation of motion allows finding three appro- ximate laws of motion, see Equations (14, 23, 32), and three approximate velocities, see Equations (15, 24, 35). The astrophysical test is performed on four spherical SNRs assumed to be spherical and the four sets of parameters are reported in Tables 2-4. The percentage of error of the Padé approximated solutions for the radius is always less than 10% with respect to the numerical exact solution, see column 6 of the three last tables. In order to produce an astrophysical prediction, the theoretical decrease in velocity for the four SNRs here analysed is evaluated, see column 7 of Tables 2-4.