L-Fuzzy Vector Subspaces and Its Fuzzy Dimension

Chun’e Huang^1*, Yan Song², Xiruo Wang²

¹College of Biochemical Engineering, Beijing Union University, Beijing, China.
²Mudanjiang Normal University, Mudanjiang, China.

DOI: 10.4236/alamt.2016.64015                

Abstract

In this paper, we introduce the definition of L-fuzzy vector subspace, define its dimension by an L-fuzzy natural number. For a finite-dimensional L-fuzzy vector subspace, we prove that the equality holds without any restricted conditions. At the same time, we deduce that the formula holds.

Keywords

L-Fuzzy Sets, L-Fuzzy Vector Subspace, L-Fuzzy Dimension

1. Introduction

Firstly, fuzzy vector subspace was introduced by Katsaras and Liu [1] . Then its pro- perties and characters were investigated (see [2] [3] [4] [5] , etc). The dimension of a fuzzy vector space was defined as a n-tuple by Lowen [6] . Subsequently, it was defined as a non-negative real number or infinity by Lubczonok [5] , and proved that the for- mula

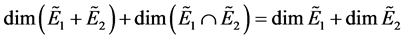(1)

is valid under certain conditions, where 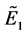and 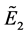are fuzzy vector spaces. Recently, basis and dimension of a fuzzy vector space were redefined as a fuzzy set and a fuzzy natural number by Shi and Huang [7] , respectively. Under the definitions, more pro- perties of (crisp) vector spaces were correct in fuzzy vector spaces.

In this paper, we generalize the results in [7] to L lattice, and prove that some for- mulas still hold in the lattice L. In particular, we present the definition of L-fuzzy vector subspace and its -fuzzy dimension. The L-fuzzy dimension of a finite dimensional fuzzy vector subspace is a fuzzy natural number. We prove that (1) holds without any re- stricted conditions and 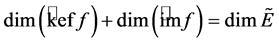holds.

2. Preliminaries

Given a set 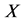and a completely distributive lattice L, we denote the power set of 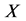and the set of all L-fuzzy sets on 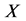(or L-sets for short) by 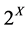and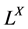, respec- tively . For any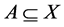, we denote the cardinality of 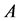by.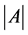

An element 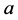in L is called a prime element if 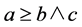implies 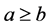or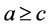. in L is called co-prime if implies or [8] . The set of non- unit prime elements in L is denoted by. The set of non-zero co-prime elements in L is denoted by.

The binary relation in L is defined as follows: for, if and only if for every subset, the relation always implies the existence of with [9] . is called the greatest minimal family of in the sense of [10] , denoted by, and. Moreover, for, we define and. In a completely distri- butive lattice, there exist and for each, and (see [10] ).

In [10] , Wang thought that and. In fact, it should be that and.

Throughout this paper, denotes a completely distributive lattice, and is a crisp vector space. We often do not distinguish a crisp subset of and its cha- racteristic function.

If and, we can define

Some properties of these cut sets can be found in [11] - [16] .

In [17] Shi introduced the concept of L-fuzzy natural numbers(denoted by), defined their operations and discussed the relation of -cut sets. We simply recall as follows: for any, ,

(1)

(2)

(3) For any and, it follows that

3. L-Fuzzy Vector Subspaces

Definition 3.1. L-fuzzy vector subspace is a pair where is a vector space on field, is a map with the property that for any, we have.

In this definition, when, L-fuzzy vector subspace is exactly the fuzzy vector subspace defined in [1] . We denote the family of L-fuzzy vector subspaces by.

Let be a member of, we denote

.

We can obtain some properties of analogous to fuzzy vector subspaces as follows.

Theorem 3.2. Let be a member of, then

(1)

(2) For any

The prove is trivial and omitted.

Remark: Since is a completely distributive lattice, the property that if , then not holds for. This can be seen from the following example.

Example 3.3. Let be a completely distributive lattice with four elements as fol- lows.

Let be an L-fuzzy vector subspace on where is defined by

We can easily check is an L-fuzzy vector subspace on. Suppose that and, then This example illustrates for L-fuzzy vector subspace,

Theorem 3.4. Let be a vector space, and. Then the follow- ing statements are equivalent:

(1) is an L-fuzzy vector subspace.

(2) (a)

(b)

(3) For any and, where is a finite natural number, we have

The prove is trivial and omitted.

In the following paper, the vector spaces we discuss are finite-dimensional. For their L-fuzzy vector subspaces, the following observation will be useful.

Remark: Let be a member of. Suppose that . Since is finite-dimensional vector space, denotes, then is a finite subset of L.

In the fact, let be a basis of, then. Suppose that is infinite, then for all, the total number of is infinite. Since is a basis of, we have. Again since is finite, the total number of is also finite. It contradicts with the hypothesis. Therefore is a finite subset of with at most values; values which can be attained at the vectors of and the maximum which is attained at 0.

Theorem 3.5. Let be a vector space, and. Then the follow- ing statements equivalent:

(1) is an L-fuzzy vector subspace.

(2) For all, is a vector space.

(3) For all, is a vector space.

(4) For all, is a vector space.

(5) For all, is a vector space.

(6) For all, is a vector space.

Proof. We prove and, the others can be proved analogously.

We show that is a vector space as follows. Suppose that, then and, i.e..

Since be an L-fuzzy vector subspace, then, we have, this means. Therefore is a vector space.

Suppose that for all, is a vector space. Let and . Since is a vector space, then if and only if . We have

Therefore is an L-fuzzy vector subspace.

Suppose that, then and. Since, then. Because is an L-fuzzy vector subspace, we can have, this implies. Thus is a vector space.

Let and. Since is a vector space, then if and only if. We have the following implications.

Therefore is an L-fuzzy vector subspace.

Theorem 3.6. Let be a vector space, be a map, , and for all. Then the following statements equivalent:

(1) is an L-fuzzy vector subspace.

(2) For all, is a vector space.

Proof. Suppose that, then, i.e.. Since for all and is an L-fuzzy vector subspace, we can know, this implies. Therefore is a vector space.

Suppose that for all, is a vector space. Let and. Since is a vector space, then if and only if . We have

Therefore is an L-fuzzy vector subspace.

We can define the operations between two L-fuzzy vector subspaces analogous to fuzzy vector subspaces.

Definition 3.7. Let be two L-fuzzy vector subspaces on. Define the intersection of and to be. Define the sum of and to be where is defined by for all

Definition 3.8. Let be two members of and. We define the direct sum of and to be where is defined by for all

Theorem 3.9. Let be two members of on. We have

(1) is a member of on.

(2) is a member of on.

The proof of the theorem is trivial and it is omitted.

Theorem 3.10. Let and be the members of. We have

(1) For all,

(2) For all,

(3) For any,

(4) For any,

Proof. The proofs of (1) and (2) are easy by the definition of and the pro- perties of L-fuzzy sets.

(3) For any, we have

(4) By the definition of the sum of L-fuzzy vector subspaces, for any we have

Theorem 3.11. Let and be two members of. Suppose that for any, we have. Then

(1)

(2)

The prove is trivial and omitted.

4. Fuzzy Dimension of L-Fuzzy Vector Subspaces

Definition 4.1. Let be the family of L-fuzzy natural number. The map is defined by

is called the L-fuzzy dimensional function of the L-fuzzy vector subspace, and is called the L-fuzzy dimension of, it is an L-fuzzy natural number. We usually use another form of as follows.

Theorem 4.2. For each and, we have

Proof. For any, let. Obviously. Next we show that Suppose that and, then there

exists such that. In this case, which implies. Thus we have

This completes the proof.

Theorem 4.3. Let the pair be a member of. Then for any

If for all, then

In particular, for any.

Proof. In order to prove. Suppose that, then . Since is a preserve-union map, there is and Because, thus. There- fore.

is obvious. Moreover, we can obtain that from the definition of

In order to prove for any, we only need to show. Since the set is finite, for any we have

Therefore

Theorem 4.4. Let be a member of. Then

In particular, for any

Proof. can be proved from the following implications.

Let. In order to show, we need to show that Suppose that. Since the number of is finite, then when the number of is finite, denotes, where for any Thus Since, then we have Further we have. Thus for any

Therefore for any,

is obvious. We show that in the follow- ing implications.

Theorem 4.5. Let and be two L-fuzzy vector subspaces. Then the following equality holds

Proof. We denote the sum of by. From Theorem 11, we know that is a L-fuzzy vector subspace. By the properties of L-fuzzy na- tural numbers, Theorem 12 and the dimensional formulation of vector spaces, we know for any,

Therefore

Definition 4.6. Suppose that is an L-fuzzy vector subspace. A map is called an L-fuzzy linear transformation, if it satisfies the following conditions:

(1) is a linear map on.

(2) For all,

Theorem 4.7. Suppose that is an L-fuzzy vector subspace, is an L-fuzzy linear transformation on, then and are L-fuzzy vector subspaces.

The prove is trivial and omitted.

Theorem 4.8. Suppose that is an L-fuzzy vector subspace, is an L-fuzzy linear transformation, then

Proof. Suppose that is a linear transformation on (crisp) vector spaces, then the equality holds. Hence, for all we have

Since is a linear transformation on, we have

Therefore.

5. Conclusion

In this paper, L-fuzzy vector subspace is defined and showed that its dimension is an L-fuzzy natural number. Based on the definitions, some good properties of crisp vector spaces are hold in a finite-dimensional L-fuzzy vector subspace. In particular, the

equality holds without any restricted conditions. At the same time, holds.

Acknowledgements

The authors would like to thank the reviewers for their valuable comments and sug- gestions.

Fund

The project is by the Science & Technology Program of Beijing Municipal Commission of Education (KM201611417007), the NNSF of China (11371002), the academic youth backbone project of Heilongjiang Education Department (1251G3036), the foundation of Heilongjiang Province (A201209).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Katsaras, A.K. and Liu, D.B. (1977) Fuzzy Vector Spaces and Fuzzy Topological Vector Spaces. Journal of Mathematical Analysis and Applications, 58, 135-146. https://doi.org/10.1016/0022-247X(77)90233-5
[2]	Lubczonok, G. and Murali, V. (2002) On Flags and Fuzzy Subspaces of Vector Spaces. Fuzzy Sets and Systems, 125, 201-207. https://doi.org/10.1016/S0165-0114(00)00129-9
[3]	Abdukhalikov, K.S., Tulenbaev, M.S. and Umirbarv, U.U. (1994) On Fuzzy Bases of Vector Spaces. Fuzzy Sets and Systems, 63, 201-206. https://doi.org/10.1016/0165-0114(94)90350-6
[4]	Abdukhalikov, K.S. (1996) The Dual of a Fuzzy Subspace. Fuzzy Sets and Systems, 82, 375-381. https://doi.org/10.1016/0165-0114(96)84977-3
[5]	Lubczonok, P. (1990) Fuzzy Vector Spaces. Fuzzy Sets and Systems, 38, 329-343. https://doi.org/10.1016/0165-0114(90)90206-L
[6]	Lowen, R. (1980) Convex Fuzzy Sets. Fuzzy Sets and Systems, 3, 291-310. https://doi.org/10.1016/0165-0114(80)90025-1
[7]	Shi, F.G. and Huang, C.E. (2010) Fuzzy Bases and the Fuzzy Dimension of Fuzzy Vector Spaces. Mathematical Communications, 15, 303-310.
[8]	Gierz, G., et al. (2003) Continuous Lattices and Domains. Encyclopedia of Mathematics and its Applications, Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511542725
[9]	Dwinger, P. (1982) Characterizations of the Complete Homomorphic Images of a Completely Distributive Complete Lattice I. Indagationes Mathematicae (Proceedings), 85, 403-414. https://doi.org/10.1016/1385-7258(82)90034-8
[10]	Wang, G.-J. (1992) Theory of Topological Molecular Lattices. Fuzzy Sets and Systems, 47, 351-376. https://doi.org/10.1016/0165-0114(92)90301-J
[11]	Huang, H.-L. and Shi, F.-G. (2008) L-Fuzzy Numbers and Their Properties. Information Sciences, 178, 1141-1151. https://doi.org/10.1016/j.ins.2007.10.001
[12]	Shi, F.-G. (2000) L-Fuzzy Relation and L-Fuzzy Subgroup. Journal of Fuzzy Mathematics, 8, 491-499.
[13]	Negoita, C.V. and Ralescu, D.A. (1975) Applications of Fuzzy Sets to Systems Analysis, Interdisciplinary Systems Research Series 11, Birkhaeuser, Basel. https://doi.org/10.1007/978-3-0348-5921-9
[14]	Shi, F.-G. (1995) Theory of Lβ-Nested Sets and Lα-Nested Sets and Its Applications. Fuzzy Systems and Mathematics, 4, 65-72. (In Chinese)
[15]	Shi, F.-G. (1996) L-Fuzzy Sets and Prime Element Nested Sets. Journal of Mathematical Research and Exposition, 16, 398-402. (In Chinese)
[16]	Shi, F.-G. (1996) Theory of Molecular Nested Sets and Its Applications. Journal of Yantai Teachers University, 1, 33-36. (In Chinese)
[17]	Shi, F.-G. (2009) A New Approach to the Fuzzification of Matroids. Fuzzy Sets and Systems, 160, 696-705. https://doi.org/10.1016/j.fss.2008.05.007