On the Quantum Mechanical Treatment of the Bateman-Morse-Feshbach Damped Oscillator with Variable Mass ()
1. Introduction
The quantum damped oscillator has been studied by many researchers to understand dissipation in quantum theory since the damped harmonic oscillator is one of the simplest systems revealing the dissipation of energy. It is well known that quantum damped harmonic oscillator is studied within two representations of the model system. One representation is the Bateman-Feshbach-Tikochinsky (BFT) oscillator (often called the Bateman oscillator) as a closed system with two degrees of freedom [1] [2] . The other representation is the Caldirola-Kanai (CK) oscillator as an open system with one degree of freedom [3] [4] [5] .
The damped harmonic oscillator (DHO) is described by 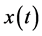 subject to the 2nd- order linear differential equation with constant coefficients, where coefficient
subject to the 2nd- order linear differential equation with constant coefficients, where coefficient 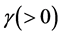 in the first derivative term is called a damping coefficient and
in the first derivative term is called a damping coefficient and 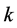 is the harmonic coefficient while
is the harmonic coefficient while 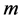 is the mass coefficient (constant):
is the mass coefficient (constant):
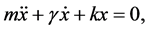 (1)
(1)
where the overdot denotes the derivative with respect to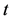 . Depending on the relation between damping and harmonic coefficients we have three different cases and the general solutions of Equation (1) are:
. Depending on the relation between damping and harmonic coefficients we have three different cases and the general solutions of Equation (1) are:
(a) The over-damping case: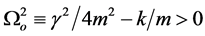 ,
,
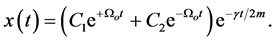 (2)
(2)
(b) The critical-damping case: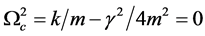 ,
,
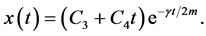 (3)
(3)
(c) The under-damping case: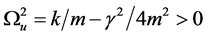 ,
,
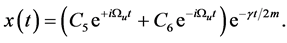 (4)
(4)
The last case is the most interesting case and Celeghini et al. [6] rigorously studied classical and quantum damped harmonic oscillator with a constant mass. In this paper we will study the case where the oscillator’s mass changes with time. When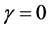 , Equation (1) is reduced to the standard harmonic oscillator equation of motion. Throughout the paper we consider the
, Equation (1) is reduced to the standard harmonic oscillator equation of motion. Throughout the paper we consider the 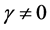 case along with a time-dependent mass
case along with a time-dependent mass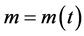 , i.e., we consider dissipation by using the simple model. The harmonic oscillator described by Equation (1) represents a dissipative system of which energy is not conserved although the
, i.e., we consider dissipation by using the simple model. The harmonic oscillator described by Equation (1) represents a dissipative system of which energy is not conserved although the 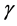 is time-independent. In order to establish the canonical for- malism for the dissipative system we have to construct a Lagrangian-Hamiltonian form in any case. Bateman’s formulation [1] resolves this problem of dissipation, where the dyna- mics of the system is described by Equation (1) in the classical theory, see below.
is time-independent. In order to establish the canonical for- malism for the dissipative system we have to construct a Lagrangian-Hamiltonian form in any case. Bateman’s formulation [1] resolves this problem of dissipation, where the dyna- mics of the system is described by Equation (1) in the classical theory, see below.
The BFT (Bateman) damped oscillator [1] [2] is regarded as an open system in which energy is dissipated by interacting with a heat bath. Bateman’s formulation [1] for the DHO resolves this problem of dissipation albeit the dynamics of the system is described by Equation (1). Bateman has shown that in order to apply the standard canonical formalism1 of classical mechanics to dissipative systems, one can double the numbers of degrees of freedom. The new degrees of freedom are assumed to represent a reservoir, also called heat bath. Applying this idea to the damped harmonic oscillator one obtains a pair of damped oscillators, so-called Bateman’s dual or mirror image system [1] , re- presented by
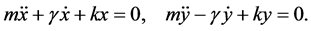 (5)
(5)
This closed system includes a primary one expressed by 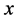 -variable and its time reversed image by
-variable and its time reversed image by ![]() -variable. According to this, the energy dissipated by the oscillator is completely absorbed at the same time by the mirror image oscillator, and thus the energy of the total system is conserved. Actually these equations can be derived from the Lagrangian:
-variable. According to this, the energy dissipated by the oscillator is completely absorbed at the same time by the mirror image oscillator, and thus the energy of the total system is conserved. Actually these equations can be derived from the Lagrangian:
![]() (6)
(6)
It should be noted that this Lagrangian does not depend on time explicitly. By Legendre transforming Equation (6), Bateman obtained the Hamiltonian:
![]() (7)
(7)
In this paper, we treat the Hamiltonian formulation and quantization of the DHO where the oscillator mass is time-dependent and study the effect of these control para- meters ![]() and
and ![]() on dissipation in quantum dissipative systems by examining the stability of vacuum state by using the simple model represented by the DHO with varying (time-dependent) mass by employing the theoretical scheme of Majima and Suzukii [11] and study dissipation in quantum dissipative systems in order to under- stand the dissipation in quantum dissipative systems.
on dissipation in quantum dissipative systems by examining the stability of vacuum state by using the simple model represented by the DHO with varying (time-dependent) mass by employing the theoretical scheme of Majima and Suzukii [11] and study dissipation in quantum dissipative systems in order to under- stand the dissipation in quantum dissipative systems.
2. Classical Theory
Let us consider the case where the oscillator’s mass is time-dependent: ![]() [12] . The kinetic momentum of the oscillator is then defined by
[12] . The kinetic momentum of the oscillator is then defined by
![]() (8)
(8)
Now we differentiate Equation (8) with respect to![]() , we obtain
, we obtain
![]() (9)
(9)
When the oscillator with variable mass is subject to the external force![]() , the equation of motion for the damped harmonic oscillator with variable mass
, the equation of motion for the damped harmonic oscillator with variable mass ![]() is given by
is given by
![]() (10)
(10)
Thus, dynamics of the damped harmonic oscillator with variable mass ![]() is governed by this equation of motion. We note that the second term in Equation (10) arises due to the oscillator mass being time-dependent. Damping occurs from the two souces
is governed by this equation of motion. We note that the second term in Equation (10) arises due to the oscillator mass being time-dependent. Damping occurs from the two souces ![]() and
and ![]() and thus the varying mass plays the same role as the damping coefficient
and thus the varying mass plays the same role as the damping coefficient![]() , that could be a control parameter for the damping.
, that could be a control parameter for the damping.
By applying Bateman’s dual oscillator formulation, the equations of motion for the dual system of the damped harmonic oscillator (10) may be expressed by the following equations of motion:
![]() (11)
(11)
If we do not employ an explicit time-dependent dissipative function, the Lagrangian leading to Equation (11) can be expressed by
![]() (12)
(12)
It is interesting to note that the form of Equation (12) is similar to Equation (6) but the mass ![]() is time-dependent:
is time-dependent:![]() .
.
Lagrange equations of motion for the Lagrangian (12) reproduce correctly the dual equations of motion (11): the first equation represents a damped harmonic oscillator with variable mass, while the second one can be considered as its time-reversed image.
Let us define the canonical momenta ![]() for our dual oscillator system by using the Lagrangian (12):
for our dual oscillator system by using the Lagrangian (12):
![]() (13)
(13)
It should be noted that these canonical momenta defined in Equation (13) are different from the kinetic momenta defined by Equation (8). In order to obtain the Hamiltonian of this dual system, we apply Legendre transformation to the Lagrangian function (12) in a following way:
![]() (14)
(14)
Expressing Equation (14) in terms of the canonical momenta ![]() with the use of Equation (13), we can obtain the Hamiltonian function of the dual system for the damped harmonic oscillators with variable mass; by this transformation the velocities
with the use of Equation (13), we can obtain the Hamiltonian function of the dual system for the damped harmonic oscillators with variable mass; by this transformation the velocities ![]() are transformed into the new variables of momenta
are transformed into the new variables of momenta![]() . The Hamiltonian function
. The Hamiltonian function ![]() of the system can then be expressed by
of the system can then be expressed by
![]() (15)
(15)
This is the extended Bateman dual-Hamiltonian for which Hamilton’s equations of motion reproduce correctly the doubled system. Since the energy of the total system is constant, the system of damped harmonic oscillator and its time-reversed image is a closed system described by the Hamiltonian function (15). We can write the canonical equations of Hamilton as follows:
![]() (16)
(16)
![]() (17)
(17)
The Hamilton equations of motion reproduce correctly the classical doubled damped harmonic oscillator systems.
The Poisson brackets of the dual system are
![]() (18)
(18)
The Poisson bracket formulation of Hamilton’s equations is given by
![]() (19)
(19)
It should be noted that the Hamiltonian (15) is a constant of the motion since![]() . It is thus concluded that the energy dissipated by the original oscillator is completely absorbed by the dual of the system.
. It is thus concluded that the energy dissipated by the original oscillator is completely absorbed by the dual of the system.
3. Quantum Theory
Let us consider the quantal case. Canonical quantization for the dual Hamiltonian ![]() in Equation (15) can be done by applying the standard quantization rules:
in Equation (15) can be done by applying the standard quantization rules:
![]() (20)
(20)
where position and momentum operators are denoted respectively by![]() ,
, ![]() , etc. The quantized Hamiltonian
, etc. The quantized Hamiltonian ![]() is then expressed by
is then expressed by
![]() (21)
(21)
where
![]() (22)
(22)
Note that the mass variable ![]() depends on time
depends on time![]() , so that the common frequency of the two damped oscillators
, so that the common frequency of the two damped oscillators ![]() defined by Equation (23) also depends on time. Here and hereafter we drop hat
defined by Equation (23) also depends on time. Here and hereafter we drop hat ![]() from the operators for the sake of simplicity of the notations.
from the operators for the sake of simplicity of the notations.
Now we introduce the pairs of the annihilation and creation operators ![]() :
:
![]() (23)
(23)
![]() (24)
(24)
![]() (25)
(25)
![]() (26)
(26)
The creation operator ![]() is the Hermitian conjugate of the annihilation operator
is the Hermitian conjugate of the annihilation operator![]() . These operators
. These operators ![]() and
and ![]() satisfy the following commutation rules:
satisfy the following commutation rules:
![]() (27)
(27)
The Hamiltonian (21) can then be expressed in terns of these creation and annihila- tion operators:
![]() (28)
(28)
where ![]() is given by Equation (23).
is given by Equation (23).
The second-quantized Hamiltonian (28) is not a simple form and it is difficult to clarify the physical meaning of each term in the particle picture. We perform the following linear canonical transformation by introducing new operators ![]() and
and![]() , which define the canonical transformations [9] :
, which define the canonical transformations [9] :
![]() (29)
(29)
and their conjugates, which resort to Equations (23)-(26). These new operators ![]() obey the same algebra as in Equation (27), that is, the following canonical commutation rules hold for the new operators
obey the same algebra as in Equation (27), that is, the following canonical commutation rules hold for the new operators![]() :
:
![]() (30)
(30)
Thus these operators construct a dual Hilbert (Fock) space![]() , where
, where ![]() on
on ![]() and
and ![]() on
on![]() .
.
The Hamiltonian (21) in the Schrödinger picture (SP) can be expressed in terms of the new operators ![]() in a simple form:
in a simple form:
![]() (31)
(31)
![]() (32)
(32)
![]() (33)
(33)
where![]() . We note that the Hamiltonians
. We note that the Hamiltonians ![]() and
and ![]() in SP are both time-dependent through
in SP are both time-dependent through ![]() and
and ![]() since they depend on the time dependent mass
since they depend on the time dependent mass![]() .
.
In order to see the effect of varying mass, let us define the vacuum states, ![]() for the system (A) spanned by the operator
for the system (A) spanned by the operator ![]() and
and ![]() for the system (B) spanned by the operator
for the system (B) spanned by the operator![]() :
:
![]() (34)
(34)
Then the vacuum state of the Hamiltonian ![]() on the dual Hilbert space can be described by the direct product of
on the dual Hilbert space can be described by the direct product of ![]() and
and![]() :
:
![]() (35)
(35)
since any operators on ![]() commutes with any operators on
commutes with any operators on![]() .
.
The SP evolution operator ![]() is generally expressed by
is generally expressed by
![]() (36)
(36)
where the symbol ![]() designates the time-ordering operator. Then we can define a vacuum state at a time
designates the time-ordering operator. Then we can define a vacuum state at a time ![]() for a dissipative system as
for a dissipative system as
![]() (37)
(37)
By using the Hamiltonain ![]() expressed in terms of the operators
expressed in terms of the operators ![]() and their conjugate operators [see Equations (31)-(33)] and the relations (30) and (34), the vacuum state (37) can be evaluated straightforwardly. The vacuum state
and their conjugate operators [see Equations (31)-(33)] and the relations (30) and (34), the vacuum state (37) can be evaluated straightforwardly. The vacuum state ![]() at time
at time ![]() is then explicitly given by
is then explicitly given by
![]() (38)
(38)
Recalling![]() , Equation (38) can be expressed by
, Equation (38) can be expressed by
![]() (39)
(39)
This equation forms the basis for further evaluation of the vacuum state of the system associated with oscillator’s variable mass and other parameters characterizing the system. In the following we consider the effect of variable mass ![]() on the dissipated system.
on the dissipated system.
4. Effect of Variable Mass
Let us study the effect of variable mass/dissipative force on the present dissipative system by looking at the vacuum states with the use of Equation (39) since the vacuum state sensitively reflects the stability (dissipation) of the system. Here we consider the following cases: (i)![]() , (ii)
, (ii)![]() , (iii)
, (iii)![]() , and (iv)
, and (iv) ![]()
![]() , where
, where ![]() is the mass value (constant) at
is the mass value (constant) at![]() .
.
We first consider the case (i) for a constant mass, i.e.,![]() . The vacuum state, Equation (39), is then given by that of the damped harmonic oscillator obtained in Ref. [11] :
. The vacuum state, Equation (39), is then given by that of the damped harmonic oscillator obtained in Ref. [11] :
![]() (40)
(40)
Figure 1 shows the time development of the vacuum state ![]() in
in![]() . Here we see that the physical vacuum
. Here we see that the physical vacuum ![]() (solid line) increases with time, reaches its maximum value and then decreases. This asymmetric shape of the
(solid line) increases with time, reaches its maximum value and then decreases. This asymmetric shape of the ![]() vs.
vs. ![]() plot can be explained as follows: As seen from Equation (38), the vacuum state
plot can be explained as follows: As seen from Equation (38), the vacuum state ![]() is the
is the
product of ![]() and
and![]() . The function
. The function ![]() (dotted line) is symmetric about
(dotted line) is symmetric about![]() , which converges 0 at
, which converges 0 at![]() , while the function
, while the function ![]() increases monotonically with time for
increases monotonically with time for![]() , where
, where ![]() takes the values between
takes the values between ![]() and
and ![]() for
for![]() . Accordingly, the monotonically increasing function
. Accordingly, the monotonically increasing function ![]() converges about
converges about ![]() for
for![]() . From these results, we can say qualitatively that
. From these results, we can say qualitatively that![]() , which is the product of
, which is the product of ![]() and
and![]() , has a peak at
, has a peak at![]() , and then decreases monotonically and converges 0 as
, and then decreases monotonically and converges 0 as ![]() goes infinity. This asymmetry of the vacuum state seen in Figure 1 is due essentially to the presence of dissipative (resistive) force. In other words, this collapse of an initial state (instability of vacuum state) is characteristic of the dissipative system considered here. We may say that in our dissipative model system, the time reversal symmetry of the vacuum state breaks down essentially due to the presence of the time reversed resistive (damping) force in the present model system.
goes infinity. This asymmetry of the vacuum state seen in Figure 1 is due essentially to the presence of dissipative (resistive) force. In other words, this collapse of an initial state (instability of vacuum state) is characteristic of the dissipative system considered here. We may say that in our dissipative model system, the time reversal symmetry of the vacuum state breaks down essentially due to the presence of the time reversed resistive (damping) force in the present model system.
Next we consider the case (ii). The vacuum state, Equation (39), is then given by
![]() (41)
(41)
It is interesting to note that the vacuum state does not change with time when the mass changes linearly with time![]() . In such a case, the vacuum state remains in a static state. See Figure 2.
. In such a case, the vacuum state remains in a static state. See Figure 2.
Next we consider the case (iii), where the mass decreases with time:![]() . The time development of the vacuum state
. The time development of the vacuum state ![]() in
in ![]() is then shown in Figure 3. In this case, the vacuum state decays abruptly in a short period of time faster than the case for a constant mass
is then shown in Figure 3. In this case, the vacuum state decays abruptly in a short period of time faster than the case for a constant mass ![]() (cp Figure 1).
(cp Figure 1).
Finally we consider the case (iv), where the mass increases exponentially with time: ![]() [see Figure 4]. The Kanai Hamiltonian [3] represents a particle of
[see Figure 4]. The Kanai Hamiltonian [3] represents a particle of
varying mass,![]() . Indeed this type of mass change explains the pe- culiar quantum mechanical features of the system represented by the Kanai Hamil- tonian, when misinterpreted as representing a particle of fixed mass subject to a dam- ping force [11] . In our formulation, Equation (39) for
. Indeed this type of mass change explains the pe- culiar quantum mechanical features of the system represented by the Kanai Hamil- tonian, when misinterpreted as representing a particle of fixed mass subject to a dam- ping force [11] . In our formulation, Equation (39) for ![]() is given by
is given by
![]() (42)
(42)
In order to study the effects of the dissipative Hamiltonian ![]() [cf. Equation (33)] on the vacuum state, one could directly compute
[cf. Equation (33)] on the vacuum state, one could directly compute ![]() by making use of Equation (39) along with the Hamiltonian
by making use of Equation (39) along with the Hamiltonian ![]() [Equation (31)]. The vacuum-to-va- cuum (V-to-V) transition amplitude (viz., the vacuum survival probability amplitude) subject to
[Equation (31)]. The vacuum-to-va- cuum (V-to-V) transition amplitude (viz., the vacuum survival probability amplitude) subject to ![]() [Equation (32)] can be calculated straightforwardly. We generally obtain the V-to-V transition amplitude in the limit
[Equation (32)] can be calculated straightforwardly. We generally obtain the V-to-V transition amplitude in the limit![]() :
:
![]() (43)
(43)
These are of dissipative nature, their time evolution being controlled by ![]() for large
for large![]() , as Equation (43) shows. This is a general expression for the V-to-V transition amplitude in the presence of external force field, from which we can study the effects of the external and the dissipative force fields through
, as Equation (43) shows. This is a general expression for the V-to-V transition amplitude in the presence of external force field, from which we can study the effects of the external and the dissipative force fields through ![]() and
and ![]() on the dissipative system expressed by the Hamiltonian
on the dissipative system expressed by the Hamiltonian ![]() [see Equations (31)-(33)].
[see Equations (31)-(33)].
It has been shown that the proper way to perform the canonical quantization of the damped harmonic oscillator is to work in the framework of Quantum Field Theory (QFT) [13] . In our formulation for many degrees of freedom, ![]() is formally (at finite volume) expressed by the free vacuum state
is formally (at finite volume) expressed by the free vacuum state ![]() at time
at time ![]() as
as ![]() , which can be calculated straightforwardly by using the explicit form of the system Hamiltonian
, which can be calculated straightforwardly by using the explicit form of the system Hamiltonian ![]() [see Equations (31)-(33)]:
[see Equations (31)-(33)]:
![]() (44)
(44)
In QFT we have to consider infinitely many degrees of freedom. Thus, by using the continuous limit relation![]() , we obtain
, we obtain
![]() (45)
(45)
provided that ![]() is finite and positive. Equation (45) means that the representation at a given time
is finite and positive. Equation (45) means that the representation at a given time ![]() is unitarily inequivalent to the representation at any different time
is unitarily inequivalent to the representation at any different time ![]() in the infinite volume limit: the system spans a whole set of unitarily inequivalent representations as time evolves (n.b. each of them is labeled by different values of
in the infinite volume limit: the system spans a whole set of unitarily inequivalent representations as time evolves (n.b. each of them is labeled by different values of![]() ).
).
5. Summary and Conclusions
To sum up, we have studied the DHO with a variable mass as a simple model for a dissipative system, following the theoretical scheme of Majima and Suzuki [11] . In Section 2, we developed the classical theory for the DHO with a variable (time-de- pendent) mass![]() . By introducing the kinetic momentum
. By introducing the kinetic momentum![]() , the equation of motion obtained for the DHO with a time-dependent mass, Equation (10), is dif- ferent from the DHO with a constant mass; as seen in Equation (10), the new force term
, the equation of motion obtained for the DHO with a time-dependent mass, Equation (10), is dif- ferent from the DHO with a constant mass; as seen in Equation (10), the new force term ![]() appears in addition to the damping force
appears in addition to the damping force![]() . This suggests the form of
. This suggests the form of ![]() plays the same role as
plays the same role as ![]() in the damping force term. It is worth to mention that the replacement of
in the damping force term. It is worth to mention that the replacement of ![]() by
by ![]() in the equation of motion (1) for the DHO is not allowed when we consider the dynamics for the DHO with a time-dependent mass (since the kinetic momentum
in the equation of motion (1) for the DHO is not allowed when we consider the dynamics for the DHO with a time-dependent mass (since the kinetic momentum ![]() the canonical momentum). The mass
the canonical momentum). The mass ![]() plays the same role as the damping constant
plays the same role as the damping constant![]() . In other words, the time-dependent mass
. In other words, the time-dependent mass ![]() could be regarded as the control parameter of damping (dissipation). Depending on the form of the time dependency of the mass, we expect that the oscillator mass
could be regarded as the control parameter of damping (dissipation). Depending on the form of the time dependency of the mass, we expect that the oscillator mass ![]() plays a passive or active role for the stability of the oscillator state and the dissipation.
plays a passive or active role for the stability of the oscillator state and the dissipation.
Introducing the canonical momenta (13) by using the obtained Lagrangian (12) for the time-dependent mass![]() , we obtained the classical Hamiltonian (15) in terms of the canonical momenta for the dissipative oscillator and its mirror image oscillator by applying the classical theory of Bateman’s dual oscillator formulation.
, we obtained the classical Hamiltonian (15) in terms of the canonical momenta for the dissipative oscillator and its mirror image oscillator by applying the classical theory of Bateman’s dual oscillator formulation.
In Section 3, we extended the theory developed in Section 2 to the quantum case, where we showed and discussed in detail how to derive the second quantized form of the Hamiltonian in terms of creation and annihilation operators ![]() for this dual system. The resultant Hamiltonian (28) is not a simple form and it is hard to clarify the physical meaning of each term in the particle picture. We showed that the second- quantized Hamiltonian (28) can be expressed in a simple form by introducing new creation and annihilation operators
for this dual system. The resultant Hamiltonian (28) is not a simple form and it is hard to clarify the physical meaning of each term in the particle picture. We showed that the second- quantized Hamiltonian (28) can be expressed in a simple form by introducing new creation and annihilation operators![]() , which construct a dual Hilbert (Fock) space
, which construct a dual Hilbert (Fock) space![]() ,
, ![]() on
on ![]() and
and ![]() on
on![]() . Then the Hamiltonian (28) can be expressed in a simple form (see Equations (31)-(33).
. Then the Hamiltonian (28) can be expressed in a simple form (see Equations (31)-(33).
In order to discuss the stability of the system arising from the change of oscillator mass in time, we focus on the change of the vacuum state of the system due to the change in the mass causing dissipation/stability of the system. We derived the general formula of the vacuum state ![]() of the system (38), which forms the basis of the present study of stability of the dissipated system. We have shown that the stability of the system due to the mass change and/or other parameters characterizing the system can be studied by looking at the behaviour of a vacuum state since the vacuum state contains useful information on the system.
of the system (38), which forms the basis of the present study of stability of the dissipated system. We have shown that the stability of the system due to the mass change and/or other parameters characterizing the system can be studied by looking at the behaviour of a vacuum state since the vacuum state contains useful information on the system.
In Section 4, we studied the effect of variable mass/dissipative force on the quantum dissipative system by using the formula (40). We considered the following cases: (i)![]() , (ii)
, (ii)![]() , (iii)
, (iii)![]() , and (iv)
, and (iv)![]() . Characte- ristic features of the time development of vacuum state
. Characte- ristic features of the time development of vacuum state ![]() for a TDM listed above are shown Figures 1-4, respectively.
for a TDM listed above are shown Figures 1-4, respectively.
Noticing that the time-dependent mass could be a control parameter for dissipation/ damping of the DHO with varying (time-dependent) mass, we developed the theory to investigate dissipation (damping) in the quantum theory and quantum dissipated system by employing the DHO as the simple model system. The time-dependent oscil- lator mass ![]() as well as the damping factor
as well as the damping factor ![]() plays an important role for damping (dissipation). Controlling these parameter, we can study the effect of dissipation in quantum dissipative systems.
plays an important role for damping (dissipation). Controlling these parameter, we can study the effect of dissipation in quantum dissipative systems.
NOTES
![]()
1In order to establish the canonical formalism for the dissipative systems we have to construct a Lagrangian-Hamiltonian form in any cases.