Leverage, Default Risk, and the Cross-Section of Equity and Firm Returns ()
1. Introduction
In this paper, I examine the relationship between the components of default risk and how they relate to the size and value factors in stock returns. The size and value factors are robust empirical factors for pricing stock returns. These factors, in addition to the market factor, lead to a three-factor asset pricing model. The most popular explanation for a multi-factor asset pricing model is time-varying risk and risk premia. In a multi- period model, an unconditional expression of risk will lead to multiple factors. Many studies including Fama and French, argue that the size and value factors are related to relative economic distress not captured by beta [1] [2] [3] .
Typically, economic distress is associated with the risk of default. Vassalou and Xing argue that most of the size premium and some of the value premium are closely related to the default risk of a firm [4] . They argue that there is a systematic positive premium on default risk that is priced in stock returns. They show empirically that default risk is priced in equity returns. Since the publication of the Vassalou and Xing paper, there have been numerous studies that debate whether default risk is priced in equity returns (e.g. Garlappi, Shu and Yan; Da and Gao; Kapadia; Garlappi and Yan; Avramov et al.; Chava and Purnanandam; and Zhang) [4] - [11] . Most notably, Campbell et al. provide evidence that firms with a higher relative risk of bankruptcy predicted from a statistical model actually have lower average returns and higher risk on average [12] . Based on their evidence, they argue that size and book-to-market premiums in stock returns are not compensation for bearing financial distress risk. They argue that the negative relationship between default risk and stock returns is an anomaly.
Several recent studies provide evidence that there is in fact a positive premium on the systematic component of default risk in stock returns (e.g. Kapadia; Chava and Purnanandam; Anginer and Yildizhan; Friewald, Wagner and Zechner) [7] [10] [13] [14] . Given the debate in the literature, it is important to dissect the underlying drivers of default risk and to examine their relationship with known pricing factors. In a structural model of default (Merton), default risk is driven by the combination of a firm’s asset volatility and its capital structure [15] . The more leverage the firm has and the more volatile the value of the firm, the higher the chance that the firm’s value will drop below its default point (liabilities owed). However, more default risk does not necessarily lead to more systematic risk. This is most clearly illustrated by examining yields on corporate debt. A yield contains an expected loss component and an expected return component1. The expected loss is directly related to default risk, while the expected return is related to the non-diversifiable component of risk2.
I argue that the components of default risk are directly related to the size and value premium. I argue that the separation of asset volatility and leverage is an important step when sorting out the relationship between size, book-to-market, and default risk. Leverage is mechanically related to the risk of equity. Covariance with the market or beta should mechanically increase as leverage increases (Hamada) [17] . However, it may be the case that firms with high leverage have low underlying business or asset risk. Regardless of the relationship between asset risk and leverage, if equity beta is measured correctly, it should pick up both components of risk. Therefore, for leverage or proxies of leverage to price equity outside of beta, it must be the case that beta is mismeasured. Ferguson and Shockley argue that excluding debt claims from the market portfolio when estimating beta causes leverage to be correlated with pricing errors in beta [18] . As leverage increases, the error in beta increases, thereby causing their relationship to be flat empirically3. I construct market portfolios that artificially inflate the weight on low-grade debt to see if this impacts the relationship with stock returns and beta. The empirical results do not support the idea that this type of measurement error is driving any proxy for leverage pricing stocks in the cross-section4.
Since beta is not capturing leverage, one could directly control for leverage in equity return asset pricing tests. However, I show that leverage choice is endogenously related to asset volatility, which is also shown by George and Hwang [21] . The endogeneity issue and other specification issues cause directly controlling for leverage in equity regressions to be a problem5. I argue that examining the cross-section of firm returns (weighted debt and equity) is the best way to mitigate mechanical differences in systematic risk related to leverage differences across firms. I show that the value premium in the cross-section of firm returns is no longer significant as a pricing factor. This is strong empirical evidence that leverage is driving the value premium and since leverage is directly related to default risk, this mechanically connects the two measures and their relationship to stock returns.
The second component of default risk, asset volatility, is not as clearly related to systematic risk of equity as leverage. I examine how asset volatility is linked to the known size and book-to-market ratios and role in returns after controlling for capital structure differences across firms. Firm size is negatively related to asset volatility and to default risk. Other studies have argued that the default risk premium in equity returns is driven by size (George and Hwang; Da and Gao) [6] [21] . My study is related to theirs, but I focus specifically on asset volatility. To be consistent with their studies, I analyze cross- sectional properties of returns excluding firms with stock prices less than five dollars. I also examine returns skipping one and two months after portfolio formation since Da and Gao argue that there are reversals after one month [6] . Finally, I control for delisting returns since I am partitioning on default risk firms. I find that the relationship between equity returns and default risk is highly dependent on including small firms and also the timing of return measurement after the portfolio formation date.
Since beta is measured with error, it is important to understand if the error is due to dynamic risk or some other form of measurement error not related to dynamic risk. I do not argue that the systematic risk of a firm is constant. In fact, if leverage changes over time, risk changes over time. In addition, the underlying dynamics of firm value (asset risk) may co-vary with the market in a different manner over time. I do argue that it is important to properly control for simple differences in leverage before deriving a complicated story about risk and risk premia dynamics. A contemporaneous paper by Choi examines firm returns and ties this to analyses of capital structure dynamics and firm risk dynamics [26] . Choi uses a conditional beta estimation approach to help sort out firm risk dynamics versus asset risk dynamics [26] . I focus on tying the two default risk components to size and book-to-market. I argue that the default risk results document by others in the literature is driven by asset volatility and not leverage. The value premium is driven more by pure differences in leverage than default risk which includes asset volatility.
I calculate firm returns in a different manner than Choi which allows for a larger cross-section and time-series of firms [26] . I measure firm returns using a firm-specific approach and an index approach, and show that the results are similar. This implies that controlling for leverage with a reasonable estimate of a firm’s debt returns is effective. This is important since we cannot truly measure a firm’s asset returns with a market based price. Many of these securities are private contracts that do not trade. I use observed corporate bond returns to estimate an econometric model of debt returns and use this as the first approach. I also use a default risk based assignment to a corporate bond index return approach. The second approach should only control for market movements, while the first should capture firm-specific movements. Using either approach, the value premium is not statistically significant in the cross-section of firm returns.
The remainder of the paper is organized as follows. First, I discuss the data used in the analysis. Second, I examine the relationship between beta, leverage, asset volatility, default risk, size, book-to-market, and stock returns. Third, I discuss the estimation of debt returns. Finally, I examine the differences in the cross-section of equity and firm returns and how they relate to default risk, size, and book-to-market.
2. Data
I use several sources of data in this study. All accounting data are from the COMPUSTAT annual file. I use the CRSP monthly stock file for equity returns. When there is a delisting event, I use the last available monthly return from the CRSP delisting file to calculate returns. I merge the CRSP and COMPUSTAT data using the link file from the merged database, which is based on CRSP permanent number and COMPUSAT GVKEY. I exclude financial firms and insurance companies from the analysis, following the prior literature. I use monthly bond returns from Reuters EJV. These data are from 2001-2005 and cover almost all traded US corporate debt.
In addition to the return and accounting data, I also use data from Moody’s KMV (MKMV). The MKMV data is linked to CRSP and COMPUSTAT using GVKEY which is provided with the data. The data from MKMV includes an estimate of an annualized Expected Default Frequency (EDF). This is the measure of default risk I use throughout the paper. Moody’s KMV uses a proprietary model to estimate a distance-to-default. This structural model of default risk includes claims to multiple types of debt instruments and preferred stock. The probability of default or EDF credit measure is based on the historical distribution of MKMV’s measure of distance-to-default and default rates. In the process of estimating a distance-to-default, MKMV estimates a measure of volatility of the firms underlying asset returns. This is done by using an iterative procedure using equity return volatility information and the structural model formulas. The two formulas relate how asset volatility (returns) and equity volatility (returns) are related. I use this estimate of asset return volatility to control for asset risk when examining leverage and beta in the cross-section6.
One issue with the MKMV data is the release of new models throughout my sample period. The EDF 8 model was established in 2006. There were some minor adjustments to the underlying model, but the major adjustment was to the empirical mapping from distance-to-default to EDF. The new mapping included more default data and a new range for the EDF credit measures7. For the majority of the analysis, I use the EDF 7 model, which restricts the data to the end of 2005. There is no reliable data for EDF 7 or 8 prior to 1970, so the sample begins then. For the firm return analysis, I use the EDF 8 model to allow for the largest sample possible. This also ensures that the analysis is not sensitive to any particular calibration of the EDF model.
When estimating beta and estimating the debt returns, I use multiple return indices. The returns on all government bonds are from the CRSP monthly government bond file. The risk-free rate is the thirty day Treasury bill rate from Federal Reserve statistical release. Corporate bond return indices are from two sources: Ibbotson Associates (pre-1989) and Lehman Brothers/Barclays Capital (post-1989). I have a complete time-series for five subsets of long-term corporate bonds: Aaa, Aa, A, Baa, and high- yield (low-grade). The Ibbotson high-yield index includes bonds rated below Baa. There is no breakdown between Ba, B, and Caa ratings. Therefore, I average the returns for the Ba, B, and Caa indices from the Lehman Brothers/Barclays Capital data to create a consistent high-yield index throughout the sample.
Table 1 lists the Pearson correlations between excess returns on each of the indices above, as well as the excess return on the CRSP equal and value-weighted stock market portfolio. Excess returns are defined as the return minus the risk-free rate. I also include changes in the risk-free rate as a proxy for innovations in the rate.
Table 1 presents the correlations for the entire period and two sub-periods. The full time-series is from January 1970 to December 2011 and the two sub-periods are from January 1970 to December 1989, and January 1990 to December 2011. I present the sub-sample results since the composition of the corporate bond market changed over time with fluctuations in the percent of speculative-grade (low-grade) bonds.
The correlation structure of the indices is similar to that found in Cornell and Green and other previous studies [29] . High-grade excess bonds returns have a high correlation with 10- and 30-year excess Treasury returns. However, low-grade bonds are less correlated with long-term Treasuries. For the full sample and both sub-samples, the correlation between excess corporate bond returns and excess returns on the CRSP stock indices monotonically increases as the credit quality of the bonds decline. The excess return on the low-grade index has a correlation of 0.54 and 0.59 with the excess
![]()
Table 1. Correlation between Indices: 1970-2011. Values are Pearson correlations over the specified sample periods. The Excess Returns on all government bonds are from the CRSP monthly government bond file. Excess returns are defined as the monthly return minus the risk free rate. The risk free rate is defined as the 30-day t-bill rate from the Federal Reserve. Corporate bond return indices are from two sources. Pre-1989, the corporate bond index returns are from Ibbotson Associates. Post-1989, the index returns are from Lehman Brothers/Barclays Capital.
return on the CRSP value-weighted and equal-weighted indices, respectively. This correlation is higher in the later sub-sample. Since the high-grade bond indices are highly correlated, I do not include all of the corporate bond indices in the multi-beta specification. I equal weight the returns for the four high-grade indices and include a high-grade (investment-grade) and low-grade (speculative-grade) index. Innovations in the risk- free rate are negatively related to all the return indices for the full sample. Only the short-term government bond index and the equal-weighted CRSP stock index are negatively related in the recent sub-sample.
3. Beta and the Components of Default Risk
Since beta should capture any asset risk and leverage effect, I examine two questions regarding the relationship between equity beta and leverage. The first question concerns estimation error in equity beta from estimating the return on the market portfolio. The second question concerns the general cross-sectional relationship between leverage and equity beta after controlling for differences in asset volatility across firms.
To address the measurement error issue related to the market portfolio, I estimate equity beta using definitions of the market portfolio which include and exclude debt returns. Based on Ferguson and Shockley, measurement error in beta related to excluding debt claims from the market portfolio is correlated with financial leverage in the cross-section [18] . By reducing this type of measurement error in beta, the role of financial leverage in the cross-section of stock returns is reduced relative to beta. This should in turn decrease the role of default risk and any factor correlated with leverage (book-to-market and size) in the cross-section of stock returns relative to beta.
I estimate equity beta using the CRSP value-weighted stock market return and compare the results when bond indices are included. I estimate a single beta and a multi-beta regression, both including debt returns. For the multi-beta specification I assume the excess return on the five proxy portfolios spans the excess return on the true market portfolio. Several papers, including Shanken, use bond and stock portfolios as proxies for the market portfolio [30] . I include a high-grade (HG) and low-grade (LG) corporate bond index as well as a long-term and short-term government bond series. The beta specifications are as follows:
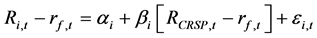 (1)
(1)
 (2)
(2)
 (3)
(3)
I use two different weighting schemes to compute the market return for (3). Ferguson and Shockley argue that the inclusion of low-grade bond returns is especially important in beta estimation due to the higher covariance with equity returns [18] . To test this, I artificially inflate the weight on low-grade debt when estimating the return for corporates. I set the weight on low-grade bond returns to 50% of the corporate bond portfolio, 25% to Baa, and 25% to A. For the government bond portfolio, I weighted the 30-year at 50% and the 1-year government bond return at 50%. The different weighting schemes for the market portfolio will highlight the sensitivity of beta to the inclusion of low-grade bond returns.
![]()
I use five-year rolling regressions to measure beta. For each five-year period, I require at least two years of data for a beta estimate. For comparability with Fama and French, I also estimate a post-ranking beta using pre-ranking beta and size sorted portfolios [24] . The final post-ranking beta estimate is the sum of this month’s and last month’s matching portfolio beta. Last month’s beta is added to overcome any issues with non-synchronous trading for the smaller stocks8. This is one technique to overcome estimation error in beta not related to the exclusion of risky debt assets from the market portfolio.
3.1. Measurement of Leverage
I measure leverage using different definitions in the analysis. Theory says the market value of leverage is the important measure when it comes to grossing up systematic risk. However, the market value of the firm is not directly observable. To overcome this issue, I use the result of the structural model equations to estimate the value of the firm. MKMV uses the estimated market value of the firm to compute asset volatility and then iteratively solve for the solution of the model. Therefore, I calculate market leverage as the market value of the firm minus the market value of equity divided by the market value of the firm.
I also compute a measure of leverage using the book value of debt as a proxy for the market value. This typically will understate the value of debt and leverage (Sweeny, Warga, and Winters) [31] . I take the book value of assets and subtract the book value of equity and short-term liabilities, then add debt in short-term liabilities. This definition covers all types of financial debt on the balance sheet. Book debt leverage is then defined as the value of debt divided by book debt plus market value of equity. I exclude operating liabilities to strictly measure financial leverage9. Finally, I measure leverage using a book value definition for debt and equity. I do this for comparability to George and Hwang and Fama and French [21] [24] . Large differences between market and book leverage will reflect large differences in book and market equity. I argue that this is one problem related to George and Hwang’s argument that leverage and stock returns have a negative unconditional relationship [21] .
I skip six months between the first stock return and the end of the accounting fiscal year to be consistent with Fama and French [24] . Therefore, any variable that uses market value of equity (
ME
) is defined as the market value at the beginning of the month over which returns are measured. This also includes the EDF credit measure. The book-to-market equity ratio (BE/ME) is defined as the fiscal year end book value of equity (BE) divided by ME. The July to June return scheme used by Fama and French skips more than six months of time for firms that do not end their fiscal year in December [24] . In addition, Fama and French use the same market and book values for the entire June to July period. I update leverage, asset volatility, EDF, ME, and BE/ME each month [24] .
Table 2 contains summary information by decile for the key variables in the analysis. Panel A contains average values sorted by the market leverage measure, Panel B the book debt leverage measure, and Panel C the book assets leverage measure. The relationship between beta and leverage is unconditionally negative for all three measures of leverage. While all the betas increase using the VW1 market portfolio, the relative trend in beta does not. Firms with leverage near 70% have betas that are lower than firms with leverage of around 5% - 10%. The beta on low-grade debt in specification (3) is relatively flat across the leverage deciles. There is very little evidence that measurement of the market portfolio is driving the beta and leverage relationship. High leverage firms are small firms with high book-to-market ratios as expected.
The average level of asset volatility may describe part of the beta puzzle, but not all of it. Asset volatility is monotonically decreasing across the leverage deciles. The firms with the highest leverage have an average asset volatility of around 20%, while the firms with the lowest leverage have an asset volatility of around 45%. This is a large difference in volatility, but this may not translate to the asset beta. EDF is increasing across the leverage deciles as expected, but the relationship is muted by the offsetting asset volatility relationship. The two components of default risk are moving in opposite directions leading to offsetting effects, but the leverage effect seems to dominate the overall impact on EDF. That is, firms with high leverage and low asset volatility have higher average default risk than firms with low leverage and high asset volatility.
Panel D contains average values of the key variables sorted by EDF. The two components of the EDF are both increasing across the EDF deciles. Asset volatility only increases marginally from 24% to 33%, but market leverage increases from around 18% to 60%. All beta measures are increasing in EDF which is inconsistent with the Campbell et al. results [12] . EDF is strongly negatively related to firm size and stock price, but positively related to book-to-market.
The data in Panel E and F are based on decile ranks using two beta measures to judge the impact of overweighting the debt claims in the market portfolio. Panel E data are based on the normal beta using the CRSP value-weighted index as the market portfolio. Panel F data are based on the VW1 market portfolio beta, which overweights low-grade debt. Leverage is negatively related to both beta measures, but the overweighting reduces
![]()
![]()
![]()
Table 2. Average Characteristics by Portfolio: 1970-2005. Portfolios are equal weighted and average values for each column are reported. Book Debt Leverage is defined as the book value of assets, minus book equity, minus short-term liabilities, plus debt in short-term liabilities, divided by the numerator plus market value of equity. Book Assets Leverage is defined as the book value of assets, minus book equity, minus short-term liabilities, plus debt in short-term liabilities, divided by book assets. CRSP VW Only beta is based on (1) from the text. VW1 and VW2 betas are estimated from weighting the market portfolio according to (3). Mutli-beta LG beta is from (2) and is the covariance on the with excess low-grade corporate bond index. Post-ranking beta is estimated as in Fama and French (1992) based on 100 double sorted size and pre-beta portfolios. Market Leverage, Empirical asset volatility, and EDF credit measures are from Moody’s KMV. Returns for the corporate bond indices are from Ibbotson and Lehman Brothers/Barclays Capital. Equity returns, prices, and shares outstanding are from the CRSP files. Accounting data are from the COMPUSTAT annual file. ME is the market value of equity and BE/ME is the book-to-market equity ratio. All betas besides the post-ranking beta are estimated on a 5-year rolling basis. Companies with stock prices below $5.00 are excluded from the sample.
this negative relationship slightly. Asset volatility is increasing as beta increases in both Panel E and F. The evidence here helps shed light on the puzzling beta and leverage relationship. The highest average beta is 2.37, with a corresponding volatility of 46%. The lowest average beta is 0.22, with a corresponding volatility of 22%. The beta does not seem to be purely related to the combination of asset volatility and leverage, which suggests asset volatility is not the best proxy for asset beta, or that there is severe mismeasurement of beta. Companies with the highest and lowest beta tend to be smaller, but book-to-market is negatively related to beta.
Table 3 contains the average cross-sectional correlations between the key variables in the analysis. The correlations confirm the relationships documented in Table 2. The average cross-sectional correlation between leverage and beta is negative for all specifications of the value-weighted portfolio. The negative correlation is reduced when including more low-grade corporate debt returns in the market portfolio, but not by significant amount. Since the portfolios are not orthogonalized and the high- and low- grade portfolios are correlated, the loading on the low-grade portfolio in the multi-beta specification is difficult to interpret.
Book-to-market is strongly negatively related to all measures of leverage, but stronger for market measures of leverage. Size is also negatively related to market leverage, but positively related to book leverage. Interestingly, asset volatility is negatively related to both size and book-to-market. Small firms with low book-to-market have higher levels of asset volatility.
Before turning to the stock return analysis, I attempt to control for asset volatility
![]()
Table 3. Average Cross-Sectional Correlations Between Key Variables: 1970-2005. Cross-sectional Pearson correlations are calculated each month and then averaged over the sample period. Book Debt Leverage is defined as the book value of assets, minus book equity, minus short-term liabilities, plus debt in short-term liabilities, divided by the numerator plus market value of equity. Book Assets Leverage is defined as the book value of assets, minus book equity, minus short-term liabilities, plus debt in short-term liabilities, divided by book assets. CRSP VW Only beta is based on (1) from the text. VW1 and VW2 betas are estimated from weighting the market portfolio according to (3). The Mutli-beta specification with 5 factors is from (2). Post-ranking beta is estimated as in Fama and French (1992) base on 100 double sorted size and pre-beta portfolios. Market Leverage, Empirical asset volatility, and EDF credit measures are from Moody’s KMV. Returns for the corporate bond indices are from Ibbotson and Lehman Brothers/Barclays Capital. Equity returns, prices, and shares outstanding are from the CRSP files. Accounting data are from the COMPUSTAT annual file. ME is the market value of equity and BE/ME is the book-to-market equity ratio. All betas besides the post-ranking beta are estimated on a 5-year rolling basis. Companies with stock prices below $5.00 are excluded from the sample.
and then sort by leverage to help understand the relationship between leverage and beta. Table 4 contains average values of key variables sorted into asset volatility quintiles first, then into market leverage quintiles within each volatility partition. As patterns in the table highlight, there is a fairly large dispersion of leverage within each volatility bucket. Leverage differences between the high and low quintiles are consistently 35 to 50%. This implies that while on average firms with low volatility of assets have high leverage, not all firms do. The firms that have high leverage in this group have very high levels of default risk and the highest average book-to-market ratios of any of the 25 double sorted portfolios.
The beta and leverage relationship is now positive after conditioning on asset volatile-
![]()
Table 4. Double Sorted Portfolios: Asset Volatility and Leverage: 1970-2005. Each month data are sorted on asset volatility and then leverage within each volatility quintile. CRSP VW Only beta is based on (3) from the text. Beta with high weight on low grade bonds is based on the VW1 weighting of the market portfolio according to (5). Market Leverage, Empirical asset volatility, and EDF credit measures are from Moody’s KMV. Returns for the corporate bond indices are from Ibbotson and Lehman Brothers/Barclays Capital. Equity returns, prices, and shares outstanding are from the CRSP files. Accounting data are from the COMPUSTAT annual file. ME is the market value of equity (from CRSP) and BE/ME is the book-to-market equity ratio. All betas are estimated on a 5-year rolling basis. Companies with stock prices below $5.00 are excluded from the sample.
ity as expected. However the increase in beta is not large enough. The 35% - 50% increase in leverage only translates into an increase in beta of around 0.30 for the low-volatility firms and much less for the high-volatility firms. If we follow the simple formula presented in most text books for un-levering beta, the resulting difference should be much larger. This implies that beta is not picking up mechanical leverage effects due to the way it is measured.
3.2. Stock Return Analysis
To formally test the Ferguson and Shockley argument that missing debt claims from the market portfolio are driving the book-to-market and size effects through their correlation with leverage, I estimate Fama and MacBeth style regressions [18] [32] . In Table 5, I report results focused on the specific measurement error issue in beta related to the market portfolio.
The key test is to measure the impact on the coefficients on size, book-to-market, and EDF after including betas measured with risky debt claims in the market portfolio. I adjust the standard errors for auto-correlation by regressing the time-series of the
![]()
Table 5. Fama-Macbeth Equity Return Cross-Sectional Regressions: 1970-2005. Each month stock returns are regressed on different beta measures, size, book-to-market and EDF to gauge the impact of measurement error. Reported coefficients are time-series averages of each months regression coefficient. Standard errors are based on Newey-West six lag adjustment for the time-series of coefficients. CRSP VW Only beta is based on (1) from the text. VW1 and VW2 betas are estimated from weighting the market portfolio according to (3). The Mutli-beta specification with 5 factors is from (2). Post-ranking beta is estimated as in Fama and French (1992) base on 100 double sorted size and pre-beta portfolios. Empirical asset volatility and EDF credit measures are from Moody’s KMV. Returns for the corporate bond indices are from Ibbotson and Lehman Brothers/Barclays Capital. Equity returns, prices, and shares outstanding are from the CRSP files. Accounting data are from the COMPUSTAT annual file. ME is the market value of equity and BE/ME is the book-to-market equity ratio. Companies with stock prices below $5.00 are excluded from the sample.
coefficients on a constant and use a six-lag Newey-West adjustment. I do not make a correction for estimation error in the betas in the first pass regression. The levels of the t-statistics are already low and the correction will likely cause the standard errors to increase further (Shanken) [33] .
The average coefficient on book-to-market is 0.301% and more than three standard errors from zero. The average coefficient on the size is −0.044% and only one standard error from zero. The lack of significant size effect is driven by the deletion of firms with stock prices under $5.00. Unreported results show that the point estimates are similar to Fama and French when including all firms in the cross-sectional regressions [24] . After including ln(EDF) in the regressions, the average point estimate on book-to- market is relatively unaffected, but the coefficient on size increases and is now statistically significant. The strong correlation between size and EDF is likely driving this result. The average coefficient on ln(EDF) is −0.062% and is only one standard error from zero. The negative sign is consistent with studies finding a negative relationship between default risk and stock returns after controlling for size and book-to-market, but the result is not statistically robust in this sample.
The key is to examine the coefficients on size, book-to-market, and EDF without beta in the regression versus when beta is in the regression. I include four specifications in Table 5. The first two include a 5-year and post ranking beta with only equity in the market portfolio. The second two include the betas discussed in the previous section that control for risky debt claims. Controlling for all three specifications of the beta estimates, the coefficients on all three factors do not change in a material way. The point estimates on the betas are positive, but none of the beta specifications lead to a statistically meaningful relationship. This is strong evidence that controlling for multiple debt claims in the market portfolio, specifically risky debt, does not alter the explanatory power of size and book-to-market in the cross-section. The formal tests reject the measurement error idea of Ferguson and Shockley [18] .
I have established that the market portfolio definition is not the cause of the measurement error issue in beta. This leaves three possible explanations for the negative cross-sectional relationship between beta and leverage. First, it is possible that firms with high asset beta have low levels of leverage either by choice or not. Second, dynamic leverage in the short run may cause unconditional beta estimation errors. Third, some other form of measurement error in beta is causing beta to not reflect market leverage.
I have provided evidence in Table 4 that firms with high levels of asset volatility have much lower levels of market leverage than firms with low asset volatility, but beta is not capturing the differences in leverage even after controlling for asset volatility10. In addition, if this is the only issue related to beta, it should still price equities in the cross-section as I have discussed previously. Therefore, we can rule out the first explanation and focus on other sources of measurement error in beta and how they related to the components of default risk.
If market leverage is dynamic in the short run, a five-year rolling estimate of beta will not capture the true equity beta of the firm. This would require leverage to change quickly at the end of the measurement period and be much different than the five-year average. To examine this further, I present average stock returns in Table 6 for deciles based on the same sorting variables in Table 2. I report nine months of stock returns. I look at the prior five month’s returns to portfolio ranking, and then the next three months following. Da and Gao argue that the results of Vassalou and Xing are essentially momentum effects in the short run [4] [6] . Choi argues that leverage spikes up for risky firms in the short run and this is not reflected in unconditional beta estimates [26] . Drobetz and Seidel make a similar argument when it comes to errors in beta estimation [34] .
The average stock returns in Panel A of Table 6 strongly suggest that the high-leve- rage firms are past losers and the low-leverage firms are past winners. The differences in average stock returns are dramatic across the deciles. However, there is a reversal in this pattern in the month of portfolio formation; the average returns of high- and low-leverage firms are similar with high-leverage firms earning slightly higher monthly returns. Therefore, using beta from a five-year regression will not capture this dynamic effect. This is not the case if we examine book assets leverage in Panel C. This will clearly impact differences in results when using book and market based measures of leverage. It may be the case that firms choose to take on less leverage due to their asset risk levels (e.g. George and Hwang; Molina) [21] [35] , but a large source of the market leverage variation comes from recent stock returns.
If we examine the pattern in Panel D, it is consistent with the leverage deciles in Panel A and B. High EDF firms have large negative recent stock returns causing spikes in market leverage. However the pattern reverses at the month of portfolio formation. There is a small positive return in the first month of the portfolio formation after deleting small firms; however, this disappears in the next two months. Since I control for delisting returns, this is not likely to be explained purely by deleting firms that actually default in the month after portfolio formation.
The main question is how to proceed to disentangle these effects and how they relate to default risk. Choi argues that leverage is increasing rapidly for high book-to-market firms when the price of risk is high, but low book-to-market firms do not experience large movements in leverage [26] . However, since most of the leverage dynamics appears to be due to changes in equity market values, both high and low book-to-market firms should experience leverage changes. Choi estimates a conditional measure of beta to pinpoint the leverage risk versus asset risk dynamics. I argue that these conditional models of beta are not needed to answer the question.
I argue that book-to-market is picking up some of the issues related to dynamic leverage better than EDF. This is because of the components of default risk; book-to- market is positively related to leverage and negatively related to asset volatility. However, size is negatively related to both components. I argue that examining the cross-section of firm returns relative to equity returns is the best way to isolate the leverage impact,
![]()
![]()
![]()
Table 6. Average Stock Returns by Portfolio: 1970-2005. Portfolios are equal weighted and average returns for each column are reported. Portfolios are formed based on the t−1 end of month levels of each of the variables. Book Debt Leverage is defined as the book value of assets, minus book equity, minus short-term liabilities, plus debt in short-term liabilities, divided by the numerator plus market value of equity. Book Assets Leverage is defined as the book value of assets, minus book equity, minus short-term liabilities, plus debt in short-term liabilities, divided by book assets. CRSP VW Only beta is based on (1) from the text. VW1 is estimated from weighting the market portfolio according to (3). Market Leverage and EDF credit measures are from Moody’s KMV. Returns for the corporate bond indices are from Ibbotson and Lehman Brothers/Barclays Capital. Equity returns, prices, and shares outstanding are from the CRSP files. Accounting data are from the COMPUSTAT annual file. ME is the market value of equity and BE/ME is the book-to-market equity ratio. All betas are estimated on a 5-year rolling basis. Companies with stock prices below $5.00 are excluded from the sample.
without the impact of asset volatility. In the next section, I use two methods for estimating firm returns and then re-test the size, book-to-market, and default risk effects.
4. Estimating Debt Returns
To calculate actual firm returns, the entire debt makeup of the firm should be considered in a weighted market value sense. Most firms have several types of debt including large portions of bank debt. Houston and James examine the debt mix of a random sample of 250 firms [36] . The mean percentage of public debt to total debt is about 14% in their sample, while bank debt is 64% of total debt on average. They classify the remaining debt claims as commercial paper and other private debt. Firms with a higher percent of bank debt tend to be smaller firms with higher book-to-market ratios.
Carey studies the credit risk of private debt. Monitoring and priority play a role in the loss rates and returns of private debt [37] . He finds that private debt has less loss severity than public debt for all grades of debt. Altman, Gande, and Saunders report recovery prices, prices at default, and prices thirty days after default for bank loans and corporate bonds from 1988-2003 [38] . They show bank loans have a higher recovery rate than senior secured bonds using all three price metrics. Finally, a study by Emery shows that when firms default on bonds, they do not always default on loans [39] . Of the firms that have defaulted on bonds and do not end up in bankruptcy, only 13% of the corporate loans are defaulted on. This is convincing evidence that, for a given firm, bank loans are less risky than corporate debt.
When calculating firm returns, given the difficulty in obtaining data on firm level private and bank loan returns, I assume all debt is public with their returns equaling the returns of corporate bonds11. Since private debt is less risky, this assumption will likely bias the results for finding a size and book-to-market effect in firm returns. In addition, I do not have data on the percentage of private debt a firm holds. Estimating the ratio of private to public debt for individual firms would increase estimation error in debt returns and hence firm returns.
Choi attempts to directly measure firm returns by constructing a weighted average of equity, public bond, and bank loan returns [26] . However, the bank loan returns are not available for much of the sample and ends up estimating bank loan returns from a regression approach. In addition, by requiring firm with publicly traded debt, it restricts the sample from a time-series perspective and from a cross-sectional perspective. I argue and provide evidence that estimating all debt returns from a model is the best method for estimating firm returns. By using an econometric model for bond returns, I am able to provide evidence on a cross-section of firm returns comparable to the Fama and French cross-section of equity returns [24] .
A Model for Corporate Bond Returns
I use the observed corporate bond returns from Reuters EJV to fit a model, then estimate bond returns from that model. This does not impose an equilibrium model on the data, which may or may not hold empirically, and allows for maximum retention of the universe of firms. In addition, although the fitted bond returns from a regression are an expected value, the expected value can be negative given the design of the model.
I use the following regression to fit the model to estimate bond returns:
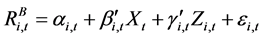 , (4)
, (4)
where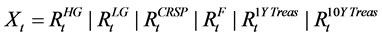 ,
, 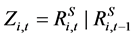 ,
, 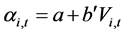 ,
, ![]() ,
, ![]() , and
, and ![]()
The structure of the model is designed to pick up the maximum amount of cross-sectional variability in returns based on market-wide and firm-specific movements. The set of X variables includes the risk-free rate and market-wide returns. Z includes concurrent and lagged firm level stock returns. Stock returns are intended to pick up firm-specific movements in cash flow or expected return news related to bond returns.
I pool the data and assume the regression coefficients are functions of firm-specific variables in V, similar to Shanken [40] . Firm-specific regressions will have a better fit, but cannot be applied to other firms not in the corporate bond sample. I report the average coefficients on firm-specific regressions as well as the pooled regressions.
I include the variables that are independent variables in the subsequent Fama-Mac- Beth regressions. This ensures that the noise induced from using fitted bond returns in the Fama-MacBeth regressions, as opposed to actual bond returns, is orthogonal to the independent variables in the regressions. Since the intercept is a function of V, the residuals are orthogonal to each component of V.
Table 7 contains the estimates of the pooled regression results. The R2 for the regres-
![]()
![]()
Table 7. Bond Return Model Regression Coefficients. Regression coefficients are from a pooled time-series cross-section model. Bond returns are averaged at the firm level and then regressed on the factors. Average firm-specific regression coefficients are also reported. The individual montly bond returns are from Reuters EJV. The returns on all government bonds indices are from the CRSP monthly government bond file. The risk free rate is defined as the thirty-day t-bill rate from CRSP. Corporate bond return indices are from two sources. Pre-1989, the corporate bond index returns are from Ibbotson Associates. Post-1989, the index returns are from Lehman Brothers/Barclays Capital. Equity returns, prices, and shares outstanding are from the CRSP files. Accounting data are from the COMPUSTAT annual file.
sion is 10%, however the mean and median R2 for the firm-specific regressions are both above 50%. I assume that![]() ,
, ![]() , and
, and ![]() are linear functions of V with an intercept. Therefore, all of the variables are included in the regression without interaction. Standard errors in the pooled regression are adjusted for clustering at the firm level.
are linear functions of V with an intercept. Therefore, all of the variables are included in the regression without interaction. Standard errors in the pooled regression are adjusted for clustering at the firm level.
Since the indices are correlated and there are three sets of interaction variables, the coefficients are difficult to interpret. The idea of the pooled regression is not to over-fit the model, but to explain as much of the bond returns as possible. Looking at the average coefficients for the firm-specific regressions helps to understand the economic relationship of the variables with the bond returns. The individual bond returns are strongly related to concurrent stock returns. The bond returns are also correlated with one month lagged returns, but the relationship is not as strong. Both the investment grade and speculative grade indices are positively related to bond returns with a similar average coefficient. The standard error of the average coefficients is lower for the speculative grade index. The largest average coefficient on the indices is on the 10-year index. Size, book-to-market, and EDF are all negatively related to bond returns.
To mitigate concerns about the econometric model for debt returns, I also use a simple approach to estimate bond returns using index returns of corporate bonds. While this method does not allow for firm-specific variation in the estimated debt returns, it helps gauge how important the debt return estimate is relative to controlling for the leverage impact on returns.
For each month, I estimate the median EDF for each rating. Then I interpolate between the ratings buckets to create an EDF minimum and maximum for each rating class in each month. I then assign each firm an index return for the rating group that the EDF falls in. I use the S&P ratings available on COMPUSTAT. Since the ratings are not available before 1985, I used the last year’s average cutoff values for the periods prior to 1985. I refer to this method in the results as the index method for firm returns.
5. Comparing the Cross-Section of Equity and Firm Returns
Using the bond return model and the index approach, I estimate monthly debt returns for each firm and form firm returns. The weight on debt returns is the book debt definition of leverage used throughout the paper, and the weight on equity returns is one minus the leverage measure. I retain a large unbiased cross-section and time-series of monthly firm returns using this method. I first re-examine the single variable sorts and compare firm and stock returns to each other.
If the size and book-to-market premiums are positive in firm returns, it supports the notion that the premiums are derived from economic risk factors unrelated to leverage. However, if the size and book-to-market premiums are non-existent in firm returns, it suggests differences in capital structure are driving the size and book-to-market premiums. One important thing to note is that the risk premium for equity returns is the firm return grossed up by leverage. Therefore, if size and book-to-market are asset risk proxies, the premium in firm returns will be less than in equity returns. Depending on the relationship between asset risk and leverage, the coefficients on size and book-to- market may automatically decrease12. However, the t-statistics in firm return regressions do not automatically decrease. There still should be a statistically positive premium on the variables if they proxy for asset risk.
Table 8 contains average firm and equity returns for ten portfolios sorted on different variables. The portfolios are formed on the three variables of interest: book-to- market, size, and EDF credit measures. The difference between the tenth and first portfolio’s average return is reported in the first column. Except for the size portfolios, the portfolios all have an equal number of observations. Following Fama and French, the size portfolios are based on the NYSE size breakpoints from CRSP [24] . To be consistent with prior studies I continue to exclude stocks with prices below $5.00.
The difference between monthly stock returns of the high and low book-to-market firms is 75 basis points and is 3.4 standard errors from zero. The two sets of firm returns are similar across the book-to-market deciles. The impact of leverage starts to show a significant reduction in average returns as book-to-market decreases. The average firm returns difference between the high and low book-to-market portfolios is
![]()
Table 8. Single Variable Sorts―Stock and Firm Returns: 1970-2011. Monthly firm returns are based on the weighted average of estimated debt returns and observed equity returns. Debt returns are calculated using two methods. The first method is an econometric model of market wide and firm-specific factors. The second method uses a risk-based allocation to an index return based on corporate debt rating. Each month the variables are sorted into 10 equally weighted portfolios, besides the market value of equity where the portfolios are based on the NYSE size breakpoints. EDF credit measures are from Moody’s KMV. Equity returns, prices, and shares outstanding are from the CRSP files. Accounting data are from the COMPUSTAT annual file. ME is the market value of equity and BE/ME is the book-to-market equity ratio. Companies with stock prices below $5.00 are excluded from the sample.
around half of the stock returns difference. The difference in monthly firm returns is 38 and 30 basis points depending on the bond return method used. The average differences in firm returns between the high and low portfolios are both less than two standard errors from zero.
The results are not as strong when examining the size returns. This is expected since book-to-market is more correlated with leverage than size. The small cap stock issue is mitigated by deleting the stocks with prices below $5.00 and by using the NYSE size breakpoints. The average return difference for stocks is −0.34% per month and the difference in firm returns is −0.33% or −0.21%, depending on the definition. Accounting for the leverage differences has a small impact on the size premium.
The results when sorting by EDF show very little difference in average returns across the EDF deciles. When accounting for the leverage impact, the difference becomes slightly negative between high and low EDF firms. These results are not consistent with the Campbell et al. results or Vassalou and Xing, but are consistent with studies that argue that the default risk results are driven by small cap firms [4] [12] .
The formal test of the return relationships is done using the Fama-MacBeth regression approach (Table 9). I regress the month-by-month cross-sectional regression coefficients on a constant and use a Newey-West six-lag adjustment for the standard errors. I include three specifications for the regressions. First, I include only ln(ME) and ln(BE/ME) as independent variables. Second, I include only ln(EDF) as an independent variable. Third, I include all three as independent variables. I have established in Table 5 that beta does not impact the regression coefficients on the three variables of interest.
In the first specification, the average coefficients on ln(BE/ME) is 0.226% for the stock return regression and drops by more than half for both sets of firm returns. The average coefficient on ln(BE/ME) is 2.8 standard errors from zero in the stock return regression and 1.2 and 1.0 for the firm returns regressions. This is strong evidence that value premium is a capital structure effect and has little to do with asset volatility. This is further supported in the third specification where ln(EDF) is included in the regressions. The coefficients and t-statistics on ln(BE/ME) are very similar to the specification without ln(EDF).
A very different pattern emerges when focusing on the ln(ME) coefficients. The negative relationship between stock returns and size is not statistically meaningful. After controlling for leverage, the size coefficient actually becomes more negative in the first firm return definition and is unaffected in the second. However, neither of the firm returns average coefficients are more than two standard errors from zero.
The default risk premium does not exist in stock returns when included alone in specification two13. After controlling for debt returns, the EDF and firm return relationship turns negative, but is not statistically significant. In the third specification including all three variables, EDF is now negatively related to stock returns. In addition, the relationship between EDF and firm returns is negative and more than two standard errors from zero for both firm returns specifications. This implies that the correlation between
![]()
Table 9. Fama-MacBeth Regressions for Stock and Firm Returns: 1970-2011. Monthly firm returns are based on the weighted average of estimated debt returns and observed equity returns. Debt returns are calculated using two methods. The first method is an econometric model of market wide and firm-specific factors. The second method uses a risk-based allocation to an index return based on corporate debt rating. Each month firm and stock returns are regressed on the set of independent variables. Reported coefficients are time-series averages of each months regression coefficient. Standard errors are based on Newey-West six lag adjustment for the time-series of coefficients. EDF credit measures are from Moody’s KMV. Equity returns, prices, and shares outstanding are from the CRSP files. Accounting data are from the COMPUSTAT annual file. ME is the market value of equity and BE/ME is the book-to-market equity ratio. Companies with stock prices below $5.00 are excluded from the sample.
EDF and size has a strong impact on the regression outcome, since book-to-market is relatively unaffected. After controlling for debt returns, both size and EDF are negatively related to returns. Since leverage is mechanically controlled for in the firm returns, this must mean the negative part is related to asset volatility.
6. Conclusions
The results in this paper establish that the separation of the components of default risk is an important step in understanding the relationship between stock returns, book-to- market, and size. Default risk is driven by leverage and asset volatility, however only one of these is directly related to systematic risk. The results demonstrate that leverage is moving over time due to changes in market values. The dynamic nature of leverage is not captured by standard measures of equity beta. I show that multiple definitions of the market portfolio do not change this result.
By focusing on leverage only, I show that a large portion of the book-to-market premium in stock returns is explained away by capital structure difference across firms. However, I show that there is no meaningful default risk premium in stock returns or firm returns. After controlling for size and book-to-market, default risk is negatively related to firm returns. Since leverage is neutralized, asset volatility is the remaining component negatively related to firm returns.
I have contributed to the literature seeking to explain the size and value premiums in stock returns with an original approach for neutralizing risk associated with financial leverage. This is the first study comparable in length and breadth to Fama and French that looks at asset or firm returns [24] . One innovation in this study is the ability to capture a large cross-section of firm’s by using debt return estimates. I use both an econometric and a characteristic based model for firm level debt returns. This new approach allows me to expand the analysis to a large set of firms. Using sources of actual debt returns limits the size of the cross-section and does not allow enough variation in firm size. The significance of the results is related to the comparability to the Fama and French study [24] . It allows a direct comparison of the results for equity and firm returns. By comparing the estimates in the same sample, it allows one to gauge the impact of leverage on the size and book to market premiums.
The new approach used to estimated debt returns also has limitations. Since we are not able to observe the actual market value of the firm, the estimates will lead to errors. The tradeoff is sample size and estimation error. In addition, while I am able to explain a portion of the book-to-market premium, there is still a positive coefficient in firm returns. It is possible that book-to-market is correlated with leverage and other firm level risk factors.
NOTES
![]()
1This ignores any tax or liquidity issues in the pricing of corporate debt.
2Hwang et al. use excess bond spreads to explain the size and value premium in equity returns using a Merton model argument that equities behave like options. They use this logic to argue that excess spreads on bonds reflect the option risk factors picked up by size and book-to-market [15] [16] .
3Stambaugh shows that inclusion of multiple types of asset returns in the market portfolio, including high-grade corporate bond returns, does not alter inference when testing the CAPM [19] . However, Stambaugh does not focus on the size and book-to-market variables [19] . In addition, Ferguson and Shockley argue that including low-grade debt returns impacts the measurement error; hence the relationship with leverage [18] .
![]()
4Aretz and Shackleton argue that omitted debt claims from the market portfolio do not theoretically undermine CAPM tests, consistent with my empirical results [20] .
5Using option pricing theory, equity returns are a non-linear function of leverage. Galai and Masulis work out the functional form for equity risk given the option pricing model [22] . The partial derivative of equity risk (as well as returns) and leverage is non-linear. Weinstein models bond returns by estimating the non-linear elasticity term multiplied by asset risk as a first-order Taylor Series expansion [23] . However, leverage still interacts with asset risk (returns) in the econometric specification. Fama and French and Bhandari both use leverage in a stock return regression and show that there is a positive relationship with market value leverage measures [24] [25] .
![]()
6A description of the model is in Crosbie and Bohn [27] . Moody’s KMV adjusts the solution to the iterative procedure further based on empirical relationships between accounting ratios and observed volatility. This final adjusted asset volatility measure is the measure used to compute distance-to-default. However, I do not use the adjusted measure since it may bias any relationship with size or the book-to-market ratio.
7See Dwyer and Qu for a full description of the enhancements to the EDF 8 model [28] .
![]()
8Post-ranking betas are computed by sorting firms into 100 size-beta portfolios. The beta for each size-beta portfolio is estimated over the full sample. Then each firm is assigned a beta based on the current size-beta portfolio they are in.
9I also measure debt using a narrower definition; long-term debt plus debt in short-term liabilities. The results throughout the paper do not change using the narrow definition of book debt.
![]()
10It is important to note that asset volatility is not the same as asset beta. This is the focus of several recent papers examining the default risk anomaly. Since I am focused on the components of default risk, I focus on separating out leverage and asset volatility affects.
![]()
11Syndicated bank loan prices are available for a subset of the sample for a recent time-series. Bank loans tend to trade infrequently and have multiple embedded options which have different characteristics than bond options.
![]()
12The amount of the decrease is a function of leverage itself and the correlation between leverage and the independent variables. The impact on the dispersion of firm returns ultimately impacts how the coefficients change since a constant is included in the regression.
![]()
13The results of the cross-sectional regressions do not change if I skip a month after portfolio formation as in Da and Gao [6] .