Asymptotic Behaviour of Solutions of Certain Third Order Nonlinear Differential Equations via Phase Portrait Analysis

Roseline Ngozi Okereke, Sadik Olaniyi Maliki

Department of Mathematics, Michael Okpara University of Agriculture, Umudike, Nigeria.

DOI: 10.4236/am.2016.718183                

Abstract

The global phase portrait describes the qualitative behaviour of the solution set for all time. In general, this is as close as we can get to solving nonlinear systems. The question of particular interest is: For what parameter values does the global phase portrait of a dynamical system change its qualitative structure? In this paper, we attempt to answer the above question specifically for the case of certain third order nonlinear differential equations of the form . The linear case where  is also considered. Our phase portrait analysis shows that under certain conditions on the coefficients as well as the function , we have asymptotic stability of solutions.

Keywords

Phase Portrait, Trajectory, Flow, Homeomorphism, Asymptotic Stability, MathCAD

1. Introduction

A line connecting the plotted points in their chronological order shows temporal evolution more clearly on the graph. The complete line on the graph (i.e. the sequence of measured values or list of successive iterates plotted on a phase space graph) describes a time path or trajectory [1] . A trajectory that comes back upon itself to form a closed loop in phase space is called an orbit [2] .

An orbit for a system usually indicates that the dynamical system under consideration is conservative. We also note that each plotted point along any trajectory has evolved directly from the preceding point. As we plot each successive point in phase space, the plotted points migrate around. Orbits and trajectories therefore reflect the movement or evolution of the dynamical system. Thus, an orbit or trajectory moves around in the phase space with time. The trajectory is a neat, concise geometric picture that describes part of the system’s history. When drawn on a graph, a trajectory must not always be smooth; instead, it can zigzag all over the phase space, mostly for discrete data [3] [4] [5] .

The phase space plot is a world that shows the trajectory and its development. Depending on various factors, different trajectories can evolve for the same system. The phase space plot and such a family of trajectories together are a phase space portrait, phase portrait, or phase diagram.

A phase space with plotted trajectories ideally shows the complete set of all possible states that a dynamical system can ever be in.

2. The Flow Defined by a Differential Equation

We next describe the notion of the flow of a system of differential equations. We begin with the linear system

(1)

The solution to the initial value problem associated with (1) is given by

The set of mappings may be regarded as describing the motion of points along trajectories of (1). This set of mappings is called the flow of the linear system (1).

2.1. Remark

The mapping satisfies the following basic properties for all:

1);

2), for all;

3) for all.

For the nonlinear system

(2)

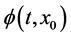we define the flow and show that it satisfies the above basic properties. Subsequently we introduce the notion of maximal interval of existence of the solution of the initial value problem

(3)

by since the end points a and b of the maximal interval generally depends on.

2.2. Definition

Let E be an open subset of and let. For, let be the solution of the initial value problem (3) defined on its maximal interval of existence. Then for, the set of mappings defined by

(4)

is called a flow of the differential Equation (2). is also referred to as the flow of the vector field.

2.3. Remark

1) We can think of the initial point as being fixed and let, then the mapping defines a solution curve or trajectory of the system (2) through the point. Naturally the mapping is identified simply with its graph in and a trajectory is visualized as a motion along a curve through the point of the phase space (Figure 1(a)). On the other hand, if we think of the point as varying throughout, then the flow of the differential Equation (2), can be viewed as the motion of all points in the set K (Figure 1(b)).

Figure 1. (a) A trajectory of the system (2); (b) The flow of the system (2).

2) If we think of the differential Equation (2) as describing the motion of a fluid, then a trajectory of (2) describes the motion of an individual particle in the fluid while the flow of the differential Equation (2) describes the motion of the entire fluid.

3) It can be shown that the basic properties (i)-(iii) of linear flows are also satisfied by nonlinear flows [6] .

4) The following theorem, provides a method of computing derivatives in coordinates.

2.4. Theorem

Given is differentiable at, then the partial derivatives all exist at and for all,

(5)

Thus, if f is a differentiable function, the derivative is given by the Jacobian matrix.

(6)

2.5. Definition

An equilibrium of the system is called hyperbolicif all eigenvalues of the Jacobian have non-zero real part.

2.6. The Hartman-Groβman Theorem

The Hartman-Groβman Theorem [7] is another very important result in the local qualitative theory of ordinary differential equations. The theorem shows that near a hyperbolic equilibrium point, the nonlinear system

(7)

has the same qualitative structure as the linear system

(8)

with. Throughout this section we shall assume that the equilibrium point has been translated to the origin.

2.7. Definition

Two autonomous systems of differential equations such as (7) and (8) are said to be topologically equivalent in a neighborhood of the origin or to have the same qualitative structure near the origin if there is a homeomorphism mapping an open set U containing the origin onto an open set V containing the origin which maps trajectories of (7) in U onto trajectories of (8) in V and preserves their orientation by time in the sense that if a trajectory is directed from to in U, then its image is directed from to in V. If the homeomorphism preserves the parameterization by time, then the systems (7) and (8) are said to be topologically conjugate in a neighborhood of the origin.

Figure 2. (a) Phase portrait of; (b) Phase portrait of.

2.8. Example

Consider the linear systems and with

Let, where.

Then one can easily check that, and letting or

It then follows that if is a solution of the first system through, then is the solution of the second system passing through. In other words maps trajectories of the first system onto trajectories of the second system and preserving the parametrization, since

(9)

The phase plane portraits of the two systems are shown in Figure 2. It clearly shows that the mapping is simply a rotation through 45˚ and thus it is a homeomorphism.

2.9. Theorem (Hartman-Groβman)

Let E be an open subset of containing the origin, suppose, and the flow of the nonlinear system. Let and the matrix has no eigenvalue with zero real part. Then there exists a homeomorphism of an open set U containing the origin onto an open set V containing the origin such that for each, there is an open interval containing zero such that for all and

(10)

i.e. maps trajectories of the nonlinear system onto trajectories of near the origin and preserves the parametrization by time.

3. Main Results

In [8] Okereke demonstrated very clearly the veracity of the Hartman-Groβman theorem by considering the simulation of the nonlinear and linearized system of ordinary differential equations in terms of their phase portrait analysis.

Consider the nonlinear system;

.

The equilibria of the above system is obtained by setting to get

Solving the above equations we obtain the equilibria as (0, 0) and.

To obtain the linearization at the origin, we begin by computing the Jacobian:

.

Evaluating the Jacobian at the first equilibrium gives

,

and therefore the linearization of our system at (0, 0) is

Since, we immediately see that the origin is a saddle for the linearized system. Evaluating the Jacobian at the second equilibrium gives

,

and therefore the linearization of our system at is

Here, thus the equilibrium point is a centre for the linearized system.

In the simulation which follows we will consider only the nontrivial equilibrium point.

3.1. MathCAD Simulation

a) The given nonlinear system can be recast in MathCAD [9] format as follows. Solution matrix is given in Figure 3.

Vector of derivatives.

Initial value of independent variable.

Terminal value of independent variable.

Vector of initial values.

Figure 3. Solution matrix for the system.

Number of solution values in.

Solution matrix.

Independent variable values.

First solution function values.

Second solution function values.

The solution profiles are depicted in Figures 4(a)-(c).

(a) (b)(c)

Figure 4. (a) Trajectory of; (b) Trajectory of; (c) Phase portrait of system near.

b) The phase portrait of the linearized system near the origin is now considered. The linearized system can be recast in MathCAD format as follows. Solution matrix is given in Figure 5.

Vector of derivatives.

Initial value of independent variable.

Terminal value of independent variable.

Vector of initial values.

Number of solution values in

kadapt Solution matrix.

Independent variable values.

First solution function values.

Second solution function values.

Figure 5. Solution matrix for the system.

The solution profiles are depicted in Figures 6(a)-(c).

(a) (b)(c)

Figure 6. (a) Trajectory of of linearized system; (b) Trajectory of of linearized system; (c) Phase portrait of linearized system near.

3.2. Observation

The phase portraits of the nonlinear system near and linearized system about the origin, show stability but not asymptotic stability. This is because the graph is a centre, and as a result, we conclude that the system is conservative. In each case we see that the phase portraits for the nonlinear and linearized system are topologically the same near the equilibrium point and respectively.

4. Phase Portrait Analysis for Stability of Third Order ODE

In this section we consider a third order linear equation

(11)

which is equivalent to the system

(12)

where a, b, c are all positive constants.

We study the asymptotic properties of the above system with the help of MathCAD simulation. The constants a, b, c are chosen such that.

4.1. Simulation

.

Vector of derivatives.

Initial value of independent variable.

Terminal value of independent variable.

Vector of initial values.

Number of solution values in

Solution matrix.

Independent variable values.

First solution function values.

Second solution function values.

Third solution function values.

The solution matrix for the above system is given in Figure 7, while the solution profiles are depicted in Figures 8(a)-(d).

Figure 7. Solution matrix for 3^rd order ODE.

Figure 8. (a) Trajectory of; (b) Trajectory of; (c) Trajectory of; (d) Phase portrait of.

4.2. The General Nonlinear Third Order ODE

We now consider the more general nonlinear third order ODE given by

(13)

where,.

We have the following theorem.

4.3. Theorem

Given that

1)

2)

3)

4)

Then every solution of Equation (13) satisfies

The proof follows that given by Omeike [10] .

Finally, when and are all constants, Equation (13) reduces to the linear equation

(14)

We have the following result following immediately from the above theorem.

4.4. Corollary

Given that

1);

2);

3).

Then every solution of Equation (13) satisfies

(15)

4.5. Remark

1) We note that (1) and (2) are the well known Routh-Hurwitz conditions [6] for the asymptotic stability of the following third-order homogeneous linear differential equation.

2) For the third order differential equation, the conditions of corollary 4.4 are clearly satisfied and from the simulation (Figures 8(a)-(c)) we can see the truth in the limit conditions (15). Figure 8(d) depicts a spiral sink in the simulation, and this further stresses the asymptotic nature of the solutions.

5. Conclusion

In this study, we investigated the stability analysis of certain third order linear and nonlinear ordinary differential equations. We employed the method of phase portrait analysis. We showed, using simulation that the Hartman-Groβman Theorem is verified, for a second order linearized system as an example, approximates the nonlinear system preserving the topological features. In the case of the third order nonlinear system, we stated appropriate theorems guaranteeing asymptotic stability of solutions. For the linear case where, our phase portrait analysis shows that under certain conditions on the coefficients as well as the function, we have asymptotic stability of solutions.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Maliki, S.O. and Nwoba, P.O. (2014) Stability Analysis of a System of Coupled Harmonic Oscillators. Pelagia Research Library Advances in Applied Science Research, 5, 195-203.
[2]	Ogundare, B.S. (2009) Qualitative and Quantitative Properties of Solutions of Ordinary Differential Equations. University of Fort Hare Alice South Africa.
[3]	Ogbu, H.M., Okereke, R.N. and Aliyu, B.Y. (2012) The Three Equivalent First Order Systems of a Third Order Scalar Equation and Its Application on Stability of Solutions of Ordinary Differential Equations. IJAPS, 4.
[4]	MathSoft, Inc. (2004) MathCAD 14 User’s Guide. http://www.mathsoft.com
[5]	Omeike, M. (2010) New Results on the Asymptotic Behaviour of a Third Order Nonlinear Differential Equation. Journal of Difference Equations and Applications, 2, 39-51. https://doi.org/10.7153/dea-02-04
[6]	Maliki, S.O. and Okereke, R.N. (2016) A Note on Differential Equation with a Large Parameter. Applied Mathematics, 7, 183-192. https://doi.org/10.4236/am.2016.73018
[7]	Maliki, S.O. (2011) Analysis of Numerical and Exact Solutions of Certain SIR and SIS Epidemic Models. Journal of Mathematical Modelling and Application, 1, 51-56.
[8]	Okereke, R.N. (2016) Lyapunov Stability Analysis of Certain Nonlinear Ordinary Differential Equations. Unpublished MSc Thesis, Michael Okpara University of Agriculture Umudike (MOUAU), Nigeria.
[9]	Cartwright, M.L. and Littlewood, J.E. (1947) On Nonlinear Differential Equations of the Second Order. II. Annals of Mathematics, 48, 472-494. https://doi.org/10.2307/1969181
[10]	Perko, L. (2001) Differential Equations and Dynamical Systems. 3rd Editon, Springer, Berlin. https://doi.org/10.1007/978-1-4613-0003-8