General Solution and Stability of Quattuordecic Functional Equation in Quasi β-Normed Spaces ()
1. Introduction
The first stability problem concerning group homomorphisms was raised by Ulam [1] in 1940. He stated that if 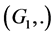 is a group and let
is a group and let  be a metric group with metric
be a metric group with metric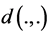 : Given
: Given , does there exist a δ > 0 such that if a mapping
, does there exist a δ > 0 such that if a mapping 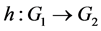 satisfies the inequality
satisfies the inequality 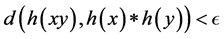 for all
for all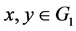 , then there exists a homomorphism
, then there exists a homomorphism 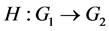 with
with 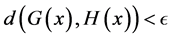 for all
for all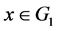 ?
?
The case of approximately additive functions was solved by D. H. Hyers [2] under the assumption that both E1 and E2 are Banach spaces. He stated that for 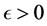 and
and 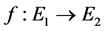 such that
such that 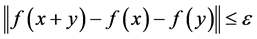 for all
for all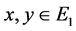 , then there exists a unique additive mapping
, then there exists a unique additive mapping 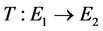 such that
such that  for all
for all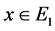 . This result is called Hyers-Ulam stability.
. This result is called Hyers-Ulam stability.
Hyers Theorem was generalized by Th. M. Rassias [3] for linear mappings by considering an unbounded Cauchy difference. The stability problem of several functional equations has been extensively investigated by a number of authors, and there are many interesting results concerning this problem [4] - [17] .
Very recently the general solution and the stability of the quintic and sextic functional equation in quasi-b-normed spaces via fixed point method were discussed by [18] . The general solution, the stability of the septic and Octic functional equations, viz.
![]()
and
![]()
in quasi-b -normed spaces were investigated by T. Z. Xu et al. [18] .
J. M. Rassias and Mohamed Eslamian discussed the general solution of a Nonic functional equation
![]()
and proved the stability of nonic functional equation [19] in quasi-b-normed spaces by applying the fixed point method.
A fixed point approach for the stability of Decic functional equation
![]()
in quasi-b-normed spaces was investigated by K. Ravi et al. [20] .
Very recently, K. Ravi and Senthil Kumar discussed the undecic and duodecic functional equation and its stability in quasi-b-normed spaces.
In this paper, the authors are interested in finding the general solution and stability of Quattuordecic functional equation
![]() (1)
(1)
where ![]() in quasi-b-normed spaces by using fixed point method.
in quasi-b-normed spaces by using fixed point method.
The functional Equation (1) is called Quattourdecic functional equation because the function ![]() satisfies the Equation (1).
satisfies the Equation (1).
In Section 2, we have given necessary definitions. In Section 3, we discuss the general solution of the functional Equation (1). In Section 4, we investigate the stability of Quattuordecic functional Equation (1) in quasi-b-normed spaces and we provide a counter example to show that the functional Equation (1) is not stable.
2. Preliminaries
We recall some basic concepts concerning quasi-b-normed spaces introduced by J. M. Rassias and H. M. Kim [14] in 2009. Let b be a fixed real number with![]() , and let K denote either R or C. Let X be linear space over K. A quasi-b-norm
, and let K denote either R or C. Let X be linear space over K. A quasi-b-norm ![]() is a real valued function on X satisfying the following three conditions:
is a real valued function on X satisfying the following three conditions:
1)![]() , for all
, for all![]() ; and
; and ![]() iff
iff![]() ,
,
2) ![]() for all
for all![]() , and all
, and all![]() ,
,
3) there is a constant ![]() such that
such that![]() .
.
For all![]() . A quasi-b -normed space is a pair
. A quasi-b -normed space is a pair![]() , where
, where ![]() is a quasi-b on X. The smallest possible K is called the modules of concavity of
is a quasi-b on X. The smallest possible K is called the modules of concavity of![]() . A quasi-b-Ba- nach space is a complete quasi-b-normed space. A quasi-b-norm
. A quasi-b-Ba- nach space is a complete quasi-b-normed space. A quasi-b-norm ![]() is called a
is called a
![]() -norm
-norm ![]() if
if ![]()
![]() .
.
In this space a quasi-b-Banach space is called a ![]() -Banach space. We can refer to [18] for the concept of quasi-normed spaces and p-Banach spaces. Given a p -norm, the formula
-Banach space. We can refer to [18] for the concept of quasi-normed spaces and p-Banach spaces. Given a p -norm, the formula ![]() gives us a translation invariant metric on X. By the Aoki-Rolewicz theorem, each quasi-norm is equal to some p-norm. Since it is much easier to work with p-norms then quasi-norms, we restrict our attention mainly to p-norms.
gives us a translation invariant metric on X. By the Aoki-Rolewicz theorem, each quasi-norm is equal to some p-norm. Since it is much easier to work with p-norms then quasi-norms, we restrict our attention mainly to p-norms.
Using fixed point theorem, Xu et al. [18] proved the following impotent lemma.
Lemma 1. Let ![]() be fixed,
be fixed, ![]() with
with![]() , and
, and ![]() be a function such that there exists an
be a function such that there exists an ![]() with
with ![]() for all
for all![]() . Let
. Let ![]() be a mapping satisfying
be a mapping satisfying
![]() (2)
(2)
Then there exists a uniquely determined mapping ![]() such that
such that
![]() (3)
(3)
3. General Solution of Functional Equation
In this section, let X and Y be vector spaces. In the following Theorem, we investigate the general solution of the functional Equation (1).
Theorem 1. A function ![]() is a solution of the Quattuordecic functional Equation (1) if and only if f is of the form
is a solution of the Quattuordecic functional Equation (1) if and only if f is of the form ![]() for all
for all![]() , where
, where ![]() is the diagonal of the 14-additive symmetric mapping
is the diagonal of the 14-additive symmetric mapping![]() .
.
Proof. Assume that f satisfies the functional Equation (1). Replacing ![]() by
by ![]() in (1), we have
in (1), we have![]() . Replacing
. Replacing ![]() by
by ![]() in (1), we get
in (1), we get
![]() (4)
(4)
Substituting ![]() by
by ![]() in (1), we obtain
in (1), we obtain
![]() (5)
(5)
Subtracting Equations (5) and (4), we get
![]() (6)
(6)
Replacing ![]() with
with ![]() in (1), one gets
in (1), one gets
![]()
and
![]() (7)
(7)
Replacing ![]() with
with ![]() in (1), one gets
in (1), one gets
![]() (8)
(8)
Subtracting the Equations (7) and (8), we obtain
![]() (9)
(9)
Replacing ![]() with
with ![]() in (1) and multiplying by 14, we have
in (1) and multiplying by 14, we have
![]() (10)
(10)
Subtracting Equations (9) and (10), we obtain
![]() (11)
(11)
Replacing ![]() with
with ![]() in (1) and multiplying by 91, we have
in (1) and multiplying by 91, we have
![]() (12)
(12)
Subtracting Equations (11) and (12), we have
![]() (13)
(13)
Replacing ![]() with
with ![]() in (1) and multiplying by 364, we have
in (1) and multiplying by 364, we have
![]() (14)
(14)
Subtracting Equations (13) and (14), we obtain
![]() (15)
(15)
Replacing ![]() with
with ![]() in (1) and multiplying by 1001, we obtain
in (1) and multiplying by 1001, we obtain
![]() (16)
(16)
Subtracting Equations (15) and (16), one gets
![]() (17)
(17)
Replacing ![]() with
with ![]() in (1) and multiplying by 2002, we have
in (1) and multiplying by 2002, we have
![]() (18)
(18)
Subtracting Equations (17) and (18), we obtain
![]() (19)
(19)
Replacing ![]() with
with ![]() in (1) and multiply by 3003, we have
in (1) and multiply by 3003, we have
![]() (20)
(20)
Subtracting Equations (19) and (20), one gets
![]() (21)
(21)
Replacing ![]() with
with ![]() in (1) and multiplying by 1716, we have
in (1) and multiplying by 1716, we have
![]() (22)
(22)
Subtracting Equations (20) and (21), we have
![]()
or
![]() (23)
(23)
On the other hand, one can rewrite the functional Equation (1) in the form
![]() (24)
(24)
for all![]() . By ( [17] , Theorems 3.5 and 3.6), f is a generalized polynomial function of degree at most 14, that is, f is of the form
. By ( [17] , Theorems 3.5 and 3.6), f is a generalized polynomial function of degree at most 14, that is, f is of the form
![]() (25)
(25)
for all![]() .
.
Here, ![]() is an arbitrary element of y and
is an arbitrary element of y and ![]() is the diagonal of the i-addi- tive symmetric map
is the diagonal of the i-addi- tive symmetric map ![]() (
(![]() ) by
) by ![]() and
and![]() , for all
, for all![]() , we get
, we get ![]() and the function f is even. Thus, we have
and the function f is even. Thus, we have
![]()
it follows that
![]()
Using Equations (25) and![]() , we obtain
, we obtain
![]()
for all ![]() and
and![]() . It follows that
. It follows that
![]()
for all![]() . Hence
. Hence![]() .
.
Conversely, assume that ![]() for all
for all![]() , where
, where ![]() is the diagonal of the 14-additive symmetric map
is the diagonal of the 14-additive symmetric map ![]() from
from
![]() (26)
(26)
and
![]()
![]()
![]()
![]()
![]()
![]()
![]()
for all ![]() and
and![]() . We see that f satisfies the Equation (1). This completes the proof of the Theorem.
. We see that f satisfies the Equation (1). This completes the proof of the Theorem.
4. Stability of Quattuordecic Functional Equation
Throughout this section, we assume that X is a linear space, Y is a ![]() Banach space with
Banach space with ![]() -norm
-norm![]() . Let K be the modulus of concavity of
. Let K be the modulus of concavity of![]() . We establish the following stability for the Quarttuordecic functional equation in quasi b-normed spaces. For a given mapping
. We establish the following stability for the Quarttuordecic functional equation in quasi b-normed spaces. For a given mapping![]() , we define the difference operator
, we define the difference operator
![]() (27)
(27)
Theorem 2. Let ![]() be fixed and
be fixed and ![]() be a function such that there exists an
be a function such that there exists an ![]() with
with ![]() for all
for all![]() . Let
. Let ![]() be a mapping satisfying
be a mapping satisfying
![]() (28)
(28)
for all![]() . Then there exists a unique Quattuordecic mapping
. Then there exists a unique Quattuordecic mapping ![]() such that
such that
![]() (29)
(29)
for all![]() , where
, where
![]() (30)
(30)
Proof. Replacing ![]() in (28), we get
in (28), we get
![]() (31)
(31)
Replacing ![]() by
by ![]() in (28), we arrive that
in (28), we arrive that
![]() (32)
(32)
Replacing ![]() by
by ![]() in (28), we have
in (28), we have
![]() (33)
(33)
From Equations (32) and (33), we obtain
![]() (34)
(34)
Replacing ![]() with
with ![]() in (28), we arrive that
in (28), we arrive that
![]() (35)
(35)
for all![]() . By (31), (34) and (35), we have
. By (31), (34) and (35), we have
![]() (36)
(36)
Replacing ![]() with
with ![]() in (28), we have
in (28), we have
![]() (37)
(37)
From (36) and (37), we arrive that
![]() (38)
(38)
Replacing ![]() with
with ![]() in (28), one finds that
in (28), one finds that
![]() (39)
(39)
Utilizing (38) and (39), we find that
![]() (40)
(40)
Replacing ![]() with
with ![]() in (28), we obtain
in (28), we obtain
![]() (41)
(41)
From (40) and (41), we arrive at
![]() (42)
(42)
Replacing ![]() with
with ![]() in (28), we obtain
in (28), we obtain
![]() (43)
(43)
Using Equations (42) and (43), we get
![]() (44)
(44)
Replacing ![]() with
with ![]() in (28), one finds that
in (28), one finds that
![]() (45)
(45)
From (44) and (45), we arrive at
![]() (46)
(46)
Replacing ![]() with
with ![]() in (28), we obtain
in (28), we obtain
![]() (47)
(47)
Using Equations (46) and (47), one gets that
![]() (48)
(48)
Replacing ![]() with
with ![]() in (28), we have
in (28), we have
![]() (49)
(49)
Using Equation (48) and (49), we obtain
![]() (50)
(50)
Replacing ![]() with
with ![]() in (28), we obtain
in (28), we obtain
![]() (51)
(51)
From (50) and (51), we arrive at
![]() (52)
(52)
Therefore,
![]()
for all![]() . By Lemma 2.1, there exists a unique mapping
. By Lemma 2.1, there exists a unique mapping ![]() such that
such that
![]()
and
![]() (53)
(53)
for all![]() . It remains to show that Q is a Quattuordecic mapping. From (28), we have
. It remains to show that Q is a Quattuordecic mapping. From (28), we have
![]() (54)
(54)
for all ![]() and
and![]() . Here
. Here![]() , for all
, for all![]() .
.
Therefore, the mapping ![]() is a Quattuordecic mapping. The following corollary is an immediate consequence of Theorem 4.1 concerning the stability of Quattuordecic functional Equation (1).
is a Quattuordecic mapping. The following corollary is an immediate consequence of Theorem 4.1 concerning the stability of Quattuordecic functional Equation (1).
Corollary 1. Let X be a quasi a-normed space with quasi a-norm![]() , and let Y be a
, and let Y be a ![]() Banach Space with
Banach Space with ![]() -norm
-norm![]() . Let
. Let ![]() be a positive number
be a positive number
with ![]() and let
and let ![]() be a mapping satisfying
be a mapping satisfying
![]()
for all![]() . Then there exists a unique quattuordecic mapping
. Then there exists a unique quattuordecic mapping ![]() such that
such that
![]() (55)
(55)
where
![]()
The following example shows that the assumption ![]() cannot be omitted in
cannot be omitted in
Corollary 4.2. This example is a modification of well known example of Gajda [6] for the additive functional inequality.
Example 1. Let ![]() be defined by
be defined by
![]() (56)
(56)
consider the function ![]() to be defined by
to be defined by
![]()
Then f satisfies the following functional inequality
![]() (57)
(57)
Proof. It is easy to see that f is bounded by ![]() on
on![]() . If
. If ![]() or
or![]() , then
, then
![]()
for all![]() . Now, suppose that
. Now, suppose that ![]() Then there exists a non-negative integer k such that
Then there exists a non-negative integer k such that
![]() (58)
(58)
Hence
![]()
and
![]()
Hence ![]() for all
for all![]() . From the definition of f and the inequality (58), we obtain that
. From the definition of f and the inequality (58), we obtain that
![]()
Therefore, f satisfies (57) for all![]() . Now, we claim that functional Equation (1) is not stable for
. Now, we claim that functional Equation (1) is not stable for ![]() in above Corollary (4.2)
in above Corollary (4.2)![]() .
.
Suppose on the contrary that there exists a Quattuordecic mapping ![]() and constant
and constant ![]() such that
such that ![]() Then there exists a constant
Then there exists a constant ![]() such that
such that ![]() for all rational numbers x (see (25)). So we obtain the following inequality
for all rational numbers x (see (25)). So we obtain the following inequality
![]() (59)
(59)
Let ![]() with
with![]() . If x is a rational number in
. If x is a rational number in![]() , then
, then ![]() for all
for all ![]() and in this case we get
and in this case we get
![]()
which contradicts the inequality (59).