Design, Manufacture and Measurements of Beta-Type Stirling Engine with Rhombic Drive Mechanism ()
1. Introduction
The continuous depletion of nonrenewable energy sources (i.e., gas, fossil fuels, coal, etc.,) is related to the economic wealth of the country involved and also to the demand for increased green products to fight global warming in order to stop or decrease pollution. The development of methods of waste heat recovery systems plays a significant role in improving the efficiency. More than 75% of the Earth’s carbon dioxide (CO2) production is directly from nonrenewable energy usage. Presently, for scientists and manufacturers, it has become an important topic of discussion to find the most suitable method of using non renewable energy sources, improving engine/machine, automotive, power plants, and so on, efficiencies fuelled by nonrenewable energy sources [1] [2] . One of the means of energy conversions is Stirling engine [3] . The Stirling engine was invented in 1816 by Robert Stirling [4] . A Stirling engine is a power machines with external combustion that operates over a closed internal gas cycle involving cyclic compression as well as the expansion of the working fluid at different temperature levels and regenerative thermodynamic cycle [1] [2] . They possess an excellent capability to operate on any form of thermal energy (solar powered or waste heat recovery sectors or fossil fuels) and the working fluid such as air, nitrogen, helium, or hydrogen. The ideal Stirling engine has advantages of high thermal efficiency, fewer emissions and being noiseless. In general, Stirling engines are available in three main types of configuration as follows [5] [6] :
・ α-type (two pistons, each in its cylinder).
・ β-type (a displacer in the same cylinder).
・ γ-Type (a piston as well as a displacer, each in its cylinder).
Stirling engines can be divided based on how the working fluid displaces within an engine. For all three engine types, there are two pistons which are set 90 degrees out of phase by some means. Each engine has advantages and disadvantages, posing unique design problems based on the details of implementation [7] .
1.1. Background Research
For the past ten years, new concepts and designs have continued to appear [8] . However, only the domestic scale Stirling electric power generating machine has obtained market potential. In a theoretical Stirling engine, chambers (for compression and expansion) are maintained at constant volume/iso-thermal conditions during heating and the cooling processes. But, neither through heating nor cooling were constant volumes or temperatures found with any degree of exactitude [9] .
Meijer invented the rhombic drive mechanism first in 1953 and later, extensive research on designs, improvements in numerical simulations and experimental investigations were carried out on the rhombic drive mechanism of the engine [10] . Shendage, D. J., et al. [11] presented an analysis of a β-type Stirling engine with the rhombic drive mechanism on the design methodology and an optimization of phase angle considering the effect of overlapping volume between expansion and compression spaces. Cinar, C. et.al. [12] manufactured and tested the β-type Stirling engine operating at atmospheric pressure with a 192 cc total swept volume. The test engine reached a maximum of 4.98 Watts at 208 rpm at 1000˚C. Extensive numerical investigations were based on Schmidt’s theory [13] [14] shown the improvements of a β-type Stirling engine performance on regenerator with successive homogeneous stainless steel wire meshes filled the space. The porous displacer does the work of a displacer and a regenerator simultaneously which delivers 20% more power and 10% more efficiency than the General Motor GPU-3 engine [5] [15] . Snyman, H., et al. [1] used the well-known Schmidt analysis and two methods (developed by Berchowitz and Urieli) for engine design to investigate scaled results of the difference between simulated and user defined engine pressure. This became an improvement on the original simulation for developing a Stirling engine design synthesis tool. Kwankaomeng, S., et al. [5] presented a design and manufacture process of a rhombic drive based on the assumptions made to simplify the theoretical modeling of the system causing inaccurate results compared to experimental data. El Hassani, H., et al. [6] studied parameter effect on a low temperature solar Stirling engine driven by a rhombic drive mechanism using theoretical analysis to investigate the variation of the machine spaces and power using thermodynamic analysis and Schmidt’s theory. The minimum values and directions about realizing the optimal phase angle were suggested for optimization of the rhombic drive mechanism and this increased power about 50%. Araoz, J. A., et al. [8] developed a non-ideal Stirling engine thermodynamic model suitable for the integration into overall energy systems using a modular methodology consisting of four modules. This novel approach permits smooth integration of the engine model with combined heat and power systems and thus it will allow overall design and optimization studies. Solmaz, H. and H. Karabulut [9] presented a β-type lever driving a Stirling engine mechanism and its thermodynamic performance for comparing with the rhombic drive engine performance. Schreiber, J. G. and S. M. Geng [16] presented a description of an RE-1000 free piston Stirling engine hydraulic output system carrying the work performed in house to characterize it. The data from the tests was intended to provide a database for the validation of Stirling cycle simulations. Raguram, A. and K. Lingeswaran [17] presented a design of a Stirling engine and solar collectors to run an automobile alternator. Demir, B. and A. Güngör [18] designed and manufactured a V-type Stirling engine using air as working fluid at a range of 1 - 3 bar charge pressure (BCP) and 700˚C to 1050˚C hot source temperature (HST). Experimental results on the variation of engine power and torque concluded that the maximum engine power was 21.334 W at 1050˚C HST and 1.5 BCP. Meijer, R. J. et al. [10] carried out designing the piston and displacer one above the other to allow the temperature and pressure variations of the working medium for separation in a Philips Stirling thermal engine. Phillip, R. F. et al. [19] has provided research involving the cycle in environmentally friendly applications of sustainable power generation for private and fleet vehicles which uses a segmented rotary displacer. Karabulut, H. et al. [20] carried out both simulation and experimentation of a new configuration of a β-type Stirling engine with a lever drive. It indicated the lowest compression ratio of these and charge pressure was found useful.
1.2. The Current Work
Based on the above literature reviews, the present study is to design, build and test the economic β-type configuration rhombic drive Stirling engine using air at atmospheric pressure to employ with bio-mass fuels in India. A full-scale engine will have to produce enough power. Since a typical application of power in remote areas is lighting, the power required to operate a 30 Watts electric bulb will be used as a goal for this engine. A survey of the market has shown that 300 Watts will be sufficient to light up one home. So, the power generation goal of the full-scale engine will be 300 Watts. In this article, we have presented a detailed aspect of progressed development (design, build and experimentation) to the final stage. Through testing of the built prototype, we determine which parameters affect performance and devise a model to predict engine behavior, so that we can use the prototype’s behavior as a baseline to raise awareness of the use of quality tools for various production companies irrespective of their size and type.
2. Rationale and Decision Scheme
2.1. Engine Decision
All of these advantages and disadvantages listed for each engine type and then some were used to objectively determine which would suit the project best. Each criterion was given a level of importance, depending on what needs are most important to meet given the specific application of the engine. These criteria and weighting factors were used in a decision matrix, listed in Table 1. The β-type scored the highest of the three engines, while the γ-type scored the lowest. Thus, the β-type was chosen to be the engine type for the project. Also, the β-type works by using a displacer to displace the air on the cold side of a container and then on the hot side. It is geared 90 degrees out of phase with the piston to essentially keep the device chasing its own tail as shown in Figure 1(a), whereas, Figure 1(b) shows a cut-away diagram of a rhombic drive β-type Stirling engine design.
The β-type Stirling engine, while maintaining the same basic operating principles as the alpha, differs primarily in that the engine has only one cylinder to contain both pistons. Since they are both required to face in the same direction and oscillate along the same axis, the pistons’ motion is set 90˚ out of phase by linking their respective connecting rods to points at a right angle to each other on the crank. Both pistons’ linkages exit the cylinder through the cold side of the engine, eliminating the need for a hot seal. For the β-type, the displacer piston leads the motion of the power piston by 90˚. The β-type cycle begins with the displacer piston all the way to the cold side and
![]()
Table 1. Engine choice decision matrix.
![]()
Figure 1. Schematic diagram of (a) β-type (b) rhombic drive β-type Stirling engine design, (1) hot cylinder wall, (2) cold cylinder wall with coolant inlet (3) outlet pipes, (4) thermal insulation separating the two cylinder ends, (5) displacer piston, (6) power piston, (7) flywheels, adapted from [21] .
the power piston halfway through its expansion stroke. Since the displacer piston exists mostly on the cold side, the majority of the working fluid sits to the hot side of the engine. Thermal energy is transferred into the working fluid, causing it to expand, exert pressure on the power piston, and force it into the position of the system’s maximum volume. This process is considered the power stroke and can be modelled as isothermal expansion for an ideal Stirling cycle. As the system reaches maximum volume, the displacer piston travels to the hot side of the engine and displaces the working fluid from the hot side to the cold side. This segment of the cycle can be idealized as constant volume displacement. As the working fluid travels from the hot side of the cylinder to the cold side, it begins to reject its thermal energy onto the cold cylinder walls. Then the working fluid loses thermal energy and thereby loses pressure, as well, the power piston makes its downward stroke and approaches the hot side of the engine, decreasing the volume of the system. While the drop in pressure from the drop in thermal energy of the working fluid does assist in carrying the system through this stage of the cycle, it is primarily completed employing the angular momentum of the flywheel and crank assembly. The system then reaches its minimum volume; this phase of the cycle can be idealized as isothermal compression of the working fluid. After the system has reached its minimum volume, the displacer piston is already on its way back to the cold side; this displaces the working fluid back toward the hot side of the engine. This part of the cycle can be modeled ideally as another period of constant volume displacement. After this, the cycle repeats itself.
2.2. Drive Decision
When analyzing the three drive configurations (rhombic drive, bell crank and free piston), each were judged on the seven selected criteria as shown in Table 2. The criteria were ranked in importance on a (1 - 10) scale with a ten being the most important. Next, the drive configurations were valued based on how they meshed with the desired criteria. The evaluation of each drive configuration was completed on a (1 - 5) scale where a ranking of five was considered to be the most desirable. After evaluating each drive configuration and applying the calculations, it was deemed that the free piston is the most plausible option for the design of the Stirling engine.
Next in line for comparison is the rhombic drive configuration as shown in Figure 1(b). The rhombic drive works both ends of the spectrum in terms of being ideal and not. The advantage of using a rhombic drive is the elimination of side thrusting seen in a bell crank. Since the configuration is well balanced, more of the kinetic energy in the rhombic drive is usable, which allows the rhombic drive to achieve a power output that is 10% higher than the bell crank at a cost of a thermal efficiency that is 0.5% less efficient than the bell crank. Additional advantages of a rhombic drive include decreases in frictional losses and improved sealability compared to the bell crank. Due to the double gearing method, the complexity of the drive configuration significantly increases. The system also requires tighter tolerances and is vulnerable to asymmetrical wear, which can lead to severe damage to the engine. The rhombic drives are more popular than the bell crank within industry, but they are not the most common due to their complexity.
![]()
Table 2. Decision matrix for the drive configuration of a β-type Stirling engine.
3. Design Configuration
3.1. β-Type Stirling Engine Design with Rhombic Drive
The aim of an engine design is to use air at atmospheric pressure using air as the working gas. Here, the Stirling engine consists of two moving lightweight pistons namely, displacer and working piston. The rhombic drive arrangement for the components and linkages of engine are very useful in providing reciprocating motion such that pistons are free from sideways acting forces. This driving mechanism can be designed for engine balance of a single acting engine as shown in Figure 1(a) consisting of displacer power piston, expansion space (hot), compression space (cold), piston rod, displacer rod driven by the rhombic mechanism. We have opted for β-type configuration where the displacer and power pistons reciprocate in the in-line concentric cylinder for engine type. In the rhombic drive mechanism, the whole assembly is symmetric (piston and displacer centerline). Therefore, inside the power piston rod, a displacer rod is placed concentrically. With the help of meshing and rotating gear wheels, the sliding of the displacer and piston rods is controlled and working fluid is directed between the spaces of hot and cold ends (expansion and compression zones), respectively, as shown in Figure 1(b). By the expansion of fluid at the hot end, the displacer rod starts moving and in turn, compresses the working fluid at the cold zone to push the piston rod to give power stroke from the engine.
The piston rod can be extracted to be useful as regards work or power. After giving the power stroke by the piston rod, the displacer rod, and using the rotating gear and flywheel, the piston rod is returned to repeat its cyclic motion to develop power strokes. The proposed Stirling engine has a single cylinder with the hot zone at its top, displacer rod, power piston rod and a pair of spur gears as detailed in Figure 1(b) without a regenerator but heat transfer to piston cylinder is enhanced by using annular fins. The details of these components and materials are illustrated in Table 3. Assembly of engine and β-type Stirling engine with rhombic drive is as shown in Figure 2.
3.2. β-Type Stirling Engine Assembly with Rhombic Drive
The β-type Stirling engine assembly with rhombic drive was made with a cost-effective.
![]()
Table 3. Components, quantity and material used.
![]()
Table 4. Specifications of β-type Stirling engine.
Thus, the ultimate effective product and manufactured parts of Stirling engine with their specifications are shown in Table 4 and Figure 3.
The rhombic drive mechanism was proposed first by the Philips Company and widely used for β-type Stirling engines as shown in Figure 4 [10] . The rhombic drive mechanism has the co-axial movement of the piston and the displacer is made quieter and requires no lubrication. The conditions of the rhombic drive mechanism for proper functioning are as follows:
1) At Φ = 0˚, the rigid rods d1 and d2 should be tall enough in order to reach the furthest point during the cycle.
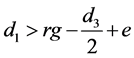 (1)
(1)
2) At Φ = 180˚, the gears used are to be far enough from each other.
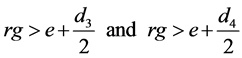 (2)
(2)
Thus, during the design of a rhombic drive mechanism, this should be followed in order to choose the rhombic drive parameters by proper selection of the cross-bar lengths d3 and d4 and the offset distance from gear center e.
![]()
Figure 3. Final product and manufactured parts of β-type Stirling engine with rhombic-drive.
![]()
Figure 4. Schematic of β-type Stirling engine with rhombic drive, adapted from [6] .
3.3. Estimation and Costing
The estimation and costing of the project merely considered prototype specifications, which in reality might increase with the working model. Considering the scope for a non-renewable source of energy in the near future, the cost can be negotiated with mass production. Table 5 illustrates the cost and estimation of the project in Rupees.
4. Experimental Results and Discussions
The prototype engine was operated with air working fluid at atmospheric pressure and heated using a LPG burner. We used a displacer piston cylinder (hot-end) heated by liquefied petroleum gas (LPG) burner and the power piston cylinder end by cooled water. Atmospheric air is used as the working gas for initial charging of the engine. The various engine characteristics are plotted in the subsequent sections.
4.1. Speed Engine
To evaluate the engine performance, different experiments were carried out by varying
![]()
Table 5. Cost and estimation of the project.
![]()
Figure 5. Speed engine variation results vs. time. The solid (red) line has been drawn to guide the eye.
![]()
Figure 6. Heater temperature variation vs. time. The solid (red) line has been drawn to guide the eye.
the flame temperature of the heat source. The results revealed that the un-pressurized engine started operation in only about 120 seconds as shown in Figure 5 with a stable polynomial regression relationship of R2 > 0.9839. Also, Figure 6 shows the time wise variation of heater temperature. After the heater temperature reached steady-state temperature, the engine runs with almost steady-speed condition. The factors which influence steady state temperature conditions are cold end, hot end temperatures and rpm of engine. When cold workspace and hot workspace temperatures indicate a grand mean temperature difference of 550˚C by minimal burner adjustment necessary to maintain that engine RPM is at or very near maximum. The engine needs approximately 20 - 23 minutes of initial run time to stabilize operation. This condition is termed steady state. Speed engine rises with the flame temperature inclement. Once the heater temperature reaches steady state about 550˚C, then the engine runs with a constant speed engine of 630 rpm. Engine speed increases with the increase of flame temperature.
4.2. Power Engine
As it seen in Figure 7, the engine started running with a speed of 280 rpm and the heater temperature of 400˚C after 120 seconds of heat application to the hot end of the engine. The data graph shows a stable polynomial regression relationship of R2 > 0.9906.
4.3. Torque Engine
From Figure 8, we see a plot of torque engine varying with the engine speed at 400˚C heater temperature with a stable polynomial regression relationship of R2 > 0.9929. The engine torque decreases with the increasing engine speed. It is found that the maximum torque was 0.245 Nm at engine speed of 280 rpm. As shown in Figure 9, the engine power is a function of speed and torque where the reduction of engine power was at the speed just below and just above 280 rpm. For a β-type Stirling engine at ambient pressure air and rhombic drive mechanism, the developed prototype provides a maximum power output of 8 Watts at 355 rpm and a hot-source temperature of 550˚C with 75 cc swept volume.
4.4. Compression Ratio Calculation
With regard to a cyclical engine, volume plays an integral role in performance characteristics. There are several different types of volumes (including maximum, minimum and displacement), compression ratio, and dead space. For a type Stirling cycle, the maximum volume is expected to be the location in which the displacement piston is at
![]()
Figure 7. Brake power variation vs. speed engine. The solid (red) line has been drawn to guide the eye.
![]()
Figure 8. Torque engine variation vs. speed engine. The solid (red) line has been drawn to guide the eye.
![]()
Figure 9. Brake power variation and torque engine vs. speed engine. The solid (blue/red) lines have been drawn to guide the eye.
the bottom dead center. Conversely, the minimum volume occurs when the displacer piston is at the top dead center. An important specification to make in order to simplify further equations is the compression ratio. Compression ratio is designated as the volume at BDC over the TDC volume, in other words, maximum volume over minimum volume. These values are calculated with the following calculations:
1) Compression ratio calculation:
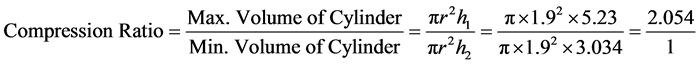 (3)
(3)
2) Thermo-dynamic calculation:
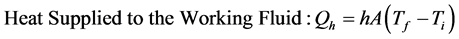 (4)
(4)
![]() (5)
(5)
3) Ideal work done by the Stirling engine calculation:
![]() (6)
(6)
where, m is the mass of working fluid, Rgt is the gas constant for the working fluid, r is the compression ratio, ΔT is the difference between the high and low temperature isotherms.
4) Actual work done by the Stirling engine calculation:
![]() (7)
(7)
where, W is the work done, F is the force and S is the distance moved by force. The centrifugal force can be calculated by
![]() (8)
(8)
Therefore,
![]()
5) Power transmitted calculated:
![]() (9)
(9)
As regards the prototype manufactured and tested, the results show that the torque required to overcome to run the engine was estimated to be 0.215 Nm. The ideal theoretical power was calculated through a formula which was 8 watts but in the actual experiment, it was found that it was much less than calculated. The results obtained from the prototype showed incompetence in overcoming the required power and torque to run the engine. The increase in temperature gradient enhances the performance of the Stirling driving force, though the following points should be considered further. For optimization of Stirling engine performance there should be tight tolerance such that the working fluid should not leave the system. The frictional losses were underrated hence the friction has to be reduced for optimal performance. The pressure of working fluid was at atmospheric pressure which should be much greater for higher power output. The calculated compression ratio was 2.05:1 which is optimal for a β-type Stirling engine. The rhombic drive mechanism was somewhat complicated in manufacturing considering the phase and tight tolerance hence the performance of the Stirling engine was much reduced.
5. Conclusions
In this work, an attempt has been made to design, manufacture and examine a low temperature difference β-type rhombic-drive Stirling engine prototype which had a swept volume of 75 cc. This work carried out for low cost design choices including low pressure, air working fluid and utilization of standard parts in construction and standard material selection. We developed various experiments and carried out these to investigate the engine performance. The experimental results revealed that the engine starts operation and attains the speed in only about 2 minutes at the flame temperature of 400˚C (752˚F) and 500˚C (932˚F) with 280 rpm and 630 rpm, respectively. We noticed that engine speed was increasing with the increment of flame temperature. We tried to develop our prototype from a variety of metals such as the engine block is made up of aluminum, gaskets and seals made of Lexan, Neoprene or natural rubber. The prototype also provided an acceptable level of working power at atmospheric air without using a regenerator increased the engine performance characteristics.
For optimizing a Stirling engine performance, we have attained tight tolerance between components such that the working fluid not leave the system and reduce the frictional losses with possible lubrication. The pressure of working fluid above atmospheric pressure for higher power output in case of air as working fluid is shown better performance. The calculated compression ratio was 2.054:1 which is optimal for a β-type Stirling engine. The rhombic drive mechanism was complex in manufacturing considering the phase and tight tolerance which reduced the performance of Stirling engine.
Conflict of Interest
The authors declare that they have no conflict of interest.