1. Introduction
Einstein’s aims are summarized by one of his most celebrated sentences: “I want to know all God’s thoughts; all the rest are just details”. With this intent, he set about elaborating a model of specific heat of solids to test the new Planck idea of energy quantization. For this reason Einstein implemented the quantization hypothesis of independent harmonic oscillators vibrating in a crystal lattice with a unique frequency. Of course he knew that this was an oversimplification of the problem; yet his primary attention was focused on the new born energy quantization, rather than on the actual vibrational spectrum of coupled oscillators. The Einstein naive model [1] is so well known that any further remark is superfluous: it is only worth quoting that the result was a brilliant validation of the energy quantization, able to predict the vanishing of specific heat at low temperatures and the empirical Dulong-Petit law of classical mechanics at high temperatures.
Shortly later, Debye [2] added the necessary “details” to the elementary Einstein approach: he refined the model introducing the statistical distribution of allowed vibrational frequencies, reasonably expected on the basis of the Born-Von Karman ideas [3] : their model of proper oscillations of linear chains of atoms with coupled motion implied the existence of lattice waves with periodic boundary condition. The group velocity of these waves introduced next the concept of phonon and the band structure of solids, which are in fact the most interesting consequences of these early studies; the characteristic temperature  is the key concept to correlate the elastic oscillations with the thermal, optical and electric properties of solids.
is the key concept to correlate the elastic oscillations with the thermal, optical and electric properties of solids.
Next, the Fermi statistics extended these achievements to the electrons of the lattice.
A comprehensive exposition of these seminal papers and their subsequent evolution are found in several textbooks, for example [4] .
The present article concerns in particular the first step of the path shortly outlined, i.e. that from Einstein to Debye. Usually the former model is acknowledged as a crucial contribution to the birth of the quantum physics; the latter model is a significant step forward not only for the accuracy with the specific heat which is calculated at low temperatures but also mostly for emphasizing the correlation between oscillation frequencies and elasticity constants of solids. Yet, simple considerations show that actually these models are more interconnected than their standard assessment taken for granted. The importance of elucidating this correlation is clear: Einstein’s reasoning has essentially quantum basis, as it is also emphasized below in this paper that, Debye’s reasoning regards a continuum body of solid matter described according to the classical elasticity theory. If these models could be someway linked, then even the oscillator frequency spectrum would automatically result entirely as a consequence of quantum principles. Just these considerations highlight the motivations of the present paper:
-to infer the Debye specific heat directly from that of the Einstein model without need of additional “ad hoc” hypotheses;
-to show that the present approach can be also extended to a system of fermions.
For sake of simplicity, the present paper assumes a monoatomic lattice of any symmetry.
2. Einstein’s Theoretical Model and Its Extension
In the Einstein model of monoatomic perfect lattice, the energy of an oscillator is in fact nothing else but the mere BE energy statistical distribution
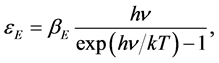 (1)
(1)
where 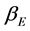 is the degeneracy factor of the distribution function. As the frequency is unique by assumption, the degeneracy is in fact given by the number of oscillators in the lattice; at the thermal equilibrium, all of them have the same energy. So, as the number of freedom degrees yields the number of possible oscillations, it follows
is the degeneracy factor of the distribution function. As the frequency is unique by assumption, the degeneracy is in fact given by the number of oscillators in the lattice; at the thermal equilibrium, all of them have the same energy. So, as the number of freedom degrees yields the number of possible oscillations, it follows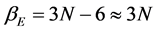 , being
, being 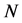 the number of lattice atoms. Here the Equation (1) is reasonably regarded as a starting point because of its general validity, direct manifestation of the quantum statistics. It is worth emphasizing that actually the lattice energy and specific heat at constant volume
the number of lattice atoms. Here the Equation (1) is reasonably regarded as a starting point because of its general validity, direct manifestation of the quantum statistics. It is worth emphasizing that actually the lattice energy and specific heat at constant volume
 (2)
(2)
have been inferred by Einstein himself, whereas the appropriate statistical distribution law was introduced much later by Bose in 1920 [5] . The Equation (2) are conveniently rewritten as follows for Avogadro’s number of oscillators
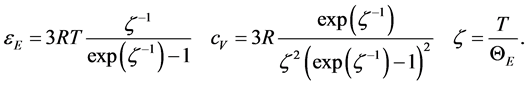 (3)
(3)
The specific heat is expressed as a correction of the asymptotic classical quantity 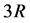 via a function of the parameter
via a function of the parameter 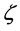 only; also,
only; also, 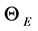 is uniquely defined by the given
is uniquely defined by the given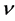 .
.
Actually, however, the real lattice consists of coupled oscillators. To introduce the coupling mechanism, consider the vibration of one atom that propagates to the first neighbors by direct interaction, and then from these latter to the next neighbors and so on. In general one atom triggers a cooperative vibrational process that involves progressively an increasing number neighbor atoms; so the progressive coupling of oscillators is described by the number of neighbors involved and by the time necessary to spread the initial perturbation, which define the wavelength of the resulting collective wave and its propagation rate throughout the lattice. Indeed the frequency 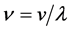 is related to the modulus of velocity
is related to the modulus of velocity  defining the wavelength
defining the wavelength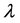 ; it suggests that just this
; it suggests that just this 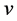 describes the propagation velocity with which the vibrational interaction spreads an oscillation wave throughout the whole crystal lattice. The fact that the velocity is a vector explains intuitively the progressing of the initial vibrational perturbation all around the trigger atom without additional hypotheses. All this is compatible with the unique frequency
describes the propagation velocity with which the vibrational interaction spreads an oscillation wave throughout the whole crystal lattice. The fact that the velocity is a vector explains intuitively the progressing of the initial vibrational perturbation all around the trigger atom without additional hypotheses. All this is compatible with the unique frequency 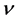 simply rewriting
simply rewriting 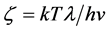 in vector form
in vector form
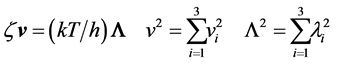 (4)
(4)
that in turn splits into the three components of the respective vectors
![]()
The components of the former Equation (4) define three orthogonal waves having different wavelengths ![]() and propagating through the lattice along orthogonal directions with related rates
and propagating through the lattice along orthogonal directions with related rates ![]() and frequencies
and frequencies![]() . In fact this is nothing else but the actualization of the previous reasoning: the vibration of the reference atom perturbs next neighbors regularly aligned along three space regular sequences of the lattice, as realistically expected in a 3D model. So, no further hypothesis has been actually introduced with respect to the original Einstein approach: in the unique frequency
. In fact this is nothing else but the actualization of the previous reasoning: the vibration of the reference atom perturbs next neighbors regularly aligned along three space regular sequences of the lattice, as realistically expected in a 3D model. So, no further hypothesis has been actually introduced with respect to the original Einstein approach: in the unique frequency ![]() are actually hidden three frequencies related to the components inherent its propagation rate vector throughout the lattice.
are actually hidden three frequencies related to the components inherent its propagation rate vector throughout the lattice.
In principle it is reasonable to guess that each ![]() is related to the cell parameters of the crystal lattice along the respective direction; the extent of
is related to the cell parameters of the crystal lattice along the respective direction; the extent of ![]() corresponds thus to the number of elementary cells whose atoms concur to propagate the vibrational motion. On the one hand
corresponds thus to the number of elementary cells whose atoms concur to propagate the vibrational motion. On the one hand ![]() are expectedly different, being related to the different spacing of crystal planes along the propagation directions of the respective vibrational waves; on the other hand, even the respective propagation rates
are expectedly different, being related to the different spacing of crystal planes along the propagation directions of the respective vibrational waves; on the other hand, even the respective propagation rates ![]() are in general different depending on the symmetry properties of the crystal lattice. Consequently, owing to the different energies inherent the respective
are in general different depending on the symmetry properties of the crystal lattice. Consequently, owing to the different energies inherent the respective ![]() of the three lattice waves, it is reasonable to rewrite the Equation (3) as the sum of three energy equations corresponding to the components of
of the three lattice waves, it is reasonable to rewrite the Equation (3) as the sum of three energy equations corresponding to the components of![]() ; hence
; hence
![]()
If![]() , the right hand side of the first equation tends to
, the right hand side of the first equation tends to![]() ; so the second equation ensures the consistency with the asymptotic behavior of the Equation (1) for
; so the second equation ensures the consistency with the asymptotic behavior of the Equation (1) for![]() . Proceeding exactly as before, the first Equation (2) turns now into
. Proceeding exactly as before, the first Equation (2) turns now into
![]() (5)
(5)
whence
![]() (6)
(6)
in this way the early Einstein equation turns into a linear combination of three functions having the same form and weighed by the arbitrary coefficients ![]() coming from the unique
coming from the unique![]() , whereas the Equation (3) are a particular case of these equations for
, whereas the Equation (3) are a particular case of these equations for ![]() and
and ![]() all equal. To give this result a reasonable physical meaning, consider that if the crystal lattice is homogeneous and isotropic there is no reason to expect that the three orthogonal waves should appear with different coefficients in the linear combination; this would mean assigning “a priori” a preferential statistical weight to one of them, i.e. to one propagation direction of the initial vibrational perturbation along one specific sequence of lattice atoms. This however seems unjustifiable. Rather, considering that the lattice directions involved by the vibrational perturbation are physically equiprobable as concerns the total energy, the hypothesis that
all equal. To give this result a reasonable physical meaning, consider that if the crystal lattice is homogeneous and isotropic there is no reason to expect that the three orthogonal waves should appear with different coefficients in the linear combination; this would mean assigning “a priori” a preferential statistical weight to one of them, i.e. to one propagation direction of the initial vibrational perturbation along one specific sequence of lattice atoms. This however seems unjustifiable. Rather, considering that the lattice directions involved by the vibrational perturbation are physically equiprobable as concerns the total energy, the hypothesis that ![]() is plausible; so, owing to the Equation (6),
is plausible; so, owing to the Equation (6),![]() . Strictly speaking, the position
. Strictly speaking, the position ![]() is in principle rigorous for an infinite single crystal with perfect lattice; however it is reasonably assumed true, at least statistically, even for real polycrystalline materials with point and line lattice defects and grain boundaries. Moreover, defining
is in principle rigorous for an infinite single crystal with perfect lattice; however it is reasonably assumed true, at least statistically, even for real polycrystalline materials with point and line lattice defects and grain boundaries. Moreover, defining
![]() (7)
(7)
the initial ratios ![]() turn into an average quantity
turn into an average quantity ![]() times the direction dependent quantities
times the direction dependent quantities![]() , which result proportional to the ratios
, which result proportional to the ratios![]() ; also, the Equation (1) splits into a new equation where the three frequencies that define
; also, the Equation (1) splits into a new equation where the three frequencies that define ![]() of
of ![]() appear explicitly. The explicit expression of the specific heat results thus to be
appear explicitly. The explicit expression of the specific heat results thus to be
![]() (8)
(8)
Also now the temperature still appears through the ratio ![]() times the quantities
times the quantities ![]() expectedly different for the three waves. In practice this expression is defined as the sum of functions of
expectedly different for the three waves. In practice this expression is defined as the sum of functions of![]() , with
, with ![]() regarded as arbitrary parameter; yet it is explicitly calculable as a function of
regarded as arbitrary parameter; yet it is explicitly calculable as a function of![]() , and thus comparable with the experimental data, once knowing the three values of
, and thus comparable with the experimental data, once knowing the three values of![]() .
.
3. Comparison with the Debye Model
A possible way to assess these results, is to compare the Equation (8) with the specific heat of the Debye model. After the early approach of Einstein, who did not introduce the frequency spectrum actually allowed in the lattice, this is the most famous and simplest model to calculate the specific heat of solids. As it is known, in this model the unique Einstein lattice frequency ![]() determining
determining ![]() is replaced by a frequency distribution according to the
is replaced by a frequency distribution according to the ![]() law; also, the interval of frequencies allowed to
law; also, the interval of frequencies allowed to ![]() is upper bounded by a postulated maximum frequency
is upper bounded by a postulated maximum frequency![]() , i.e.
, i.e.![]() . This model, in agreement with that based on the Born-Von Karman theoretical background almost simultaneously developed, is so known that the basic results only are reported here without further comments. Owing to the actual existence of several frequencies in principle admissible, the lattice vibrational energy is obtained integrating
. This model, in agreement with that based on the Born-Von Karman theoretical background almost simultaneously developed, is so known that the basic results only are reported here without further comments. Owing to the actual existence of several frequencies in principle admissible, the lattice vibrational energy is obtained integrating ![]() over the given frequency spectrum
over the given frequency spectrum
![]() (9)
(9)
here ![]() is still the degeneracy factor of the BE distribution. Trivial manipulations of these formulas yield thus the well known result
is still the degeneracy factor of the BE distribution. Trivial manipulations of these formulas yield thus the well known result
![]()
Also in this case ![]() is expressed in
is expressed in ![]() units. Normalizing
units. Normalizing ![]() to obtain again the classical asymptotic limit
to obtain again the classical asymptotic limit ![]() for
for![]() , one finds
, one finds ![]() and thus
and thus
![]() (10)
(10)
The Equations (3) and (10) differ for two reasons: because of their different ![]() profiles, especially at
profiles, especially at![]() , and because of their different inflexion temperatures calculated via
, and because of their different inflexion temperatures calculated via![]() . Indeed
. Indeed
![]() (11)
(11)
with notation emphasizing that the values are calculated at the inflexion points of the curves ![]() and
and ![]() vs
vs![]() . In general the inflection point of
. In general the inflection point of ![]() vs
vs ![]() has significant physical meaning, as it marks the transition between quantum and classical behavior of the oscillators: correspondingly, the rising rate of specific heat
has significant physical meaning, as it marks the transition between quantum and classical behavior of the oscillators: correspondingly, the rising rate of specific heat ![]() for
for ![]() attains its maximum value just at
attains its maximum value just at![]() , beyond which it decreases and tends to vanish asymptotically when
, beyond which it decreases and tends to vanish asymptotically when ![]() reaches the classical Dulong-Petit limit for
reaches the classical Dulong-Petit limit for![]() . The Figure 1 emphasizes that the respective curves not only have different
. The Figure 1 emphasizes that the respective curves not only have different ![]() profiles but are also shifted along the
profiles but are also shifted along the ![]() axis, although tending both to the same asymptotic limit for
axis, although tending both to the same asymptotic limit for![]() . On the one hand, the physical reasons of the intrinsic disagreement of
. On the one hand, the physical reasons of the intrinsic disagreement of ![]() and
and ![]() especially at low
especially at low ![]() are well known, in particular as concerns
are well known, in particular as concerns![]() . On the other hand, however, the question arises: does the modified Equation (8) overcome both discrepancies without need of any “ad hoc” hypothesis, e.g. taking advantage of the fact that expectedly
. On the other hand, however, the question arises: does the modified Equation (8) overcome both discrepancies without need of any “ad hoc” hypothesis, e.g. taking advantage of the fact that expectedly![]() ?
?
Assessing comparatively the Equations (8) and (10) needs a general reasoning to guess the numerical values of the amounts ![]() and to calculate both equations for arbitrary values of the free parameter
and to calculate both equations for arbitrary values of the free parameter ![]() only; this latter becomes thus the unique variable as a function of which are compared
only; this latter becomes thus the unique variable as a function of which are compared ![]() and
and![]() . Assuming that the energies of the oscillators are quantized, it is reasonable to expect that one of them, say
. Assuming that the energies of the oscillators are quantized, it is reasonable to expect that one of them, say![]() , accounts for the zero point energy in the lattice, whereas the remaining two,
, accounts for the zero point energy in the lattice, whereas the remaining two, ![]() and
and![]() , account for the ground vibrational energy level of the lattice; i.e.
, account for the ground vibrational energy level of the lattice; i.e. ![]() should be
should be
![]()
Figure 1. Specific heats ![]() of the Debye and Einstein models vs
of the Debye and Einstein models vs![]() .
.
one half of![]() . In effect this conclusion is expectable at
. In effect this conclusion is expectable at![]() , because the lattice can be in the plain zero point energy state at the absolute zero only. So the actual vibrational level of the lattice is still one only,
, because the lattice can be in the plain zero point energy state at the absolute zero only. So the actual vibrational level of the lattice is still one only, ![]() , exactly as in the early Einstein model; yet it appears here with the zero point energy too, as it is reasonably understandable. Since a free oscillator is characterized by the frequencies
, exactly as in the early Einstein model; yet it appears here with the zero point energy too, as it is reasonably understandable. Since a free oscillator is characterized by the frequencies![]() , assume that the frequencies
, assume that the frequencies ![]() fit the condition (7) putting
fit the condition (7) putting
![]() (12)
(12)
if so, then
![]()
In the following we take ![]() to implement in the next calculations the condition of minimum vibrational energy. The third Equation (7) reads thus
to implement in the next calculations the condition of minimum vibrational energy. The third Equation (7) reads thus
![]() (13)
(13)
so the Equation (8) results expressed as the sum of one zero point wave, function of![]() , and two identical vibrational waves, both at the ground energy level, functions of
, and two identical vibrational waves, both at the ground energy level, functions of![]() . It turns therefore into
. It turns therefore into
![]() (14)
(14)
In principle, even without specifying the constant parameter![]() , a universal curve of specific heat is still obtained as a function of the ratio
, a universal curve of specific heat is still obtained as a function of the ratio ![]() only
only
![]()
in practice, however, assessing the validity of the Equation (14) by direct comparison with the experimental data of various materials as a function of ![]() requires knowing
requires knowing![]() . In this respect, note that for the parameter
. In this respect, note that for the parameter ![]() holds the boundary condition
holds the boundary condition ![]() at the inflexion point
at the inflexion point ![]() of the curve
of the curve ![]() vs
vs![]() . A trivial calculation yields
. A trivial calculation yields
![]()
A simple chance to assess the Equation (14) is to compare it with the Debye Equation (10): this is possible if ![]() is known, so that both equations are calculable as a function of
is known, so that both equations are calculable as a function of ![]() only. To this aim regard preliminarily
only. To this aim regard preliminarily ![]() as best fit parameter, whose numerical value will be justified in the next section together with the physical meaning of
as best fit parameter, whose numerical value will be justified in the next section together with the physical meaning of ![]() and
and ![]() to which is related
to which is related![]() . Put therefore
. Put therefore
![]() (15)
(15)
which yields
![]() (16)
(16)
Of course this intentional choice of ![]() makes
makes ![]() consistent with the Debye temperature
consistent with the Debye temperature ![]() in the Equation (11), whence the importance of justifying below the Equation (15) from a theoretical point of view. The Equations (8) and (14) calculated with the given value of
in the Equation (11), whence the importance of justifying below the Equation (15) from a theoretical point of view. The Equations (8) and (14) calculated with the given value of ![]() have been plotted together in the range
have been plotted together in the range![]() , which seems appropriate to compare lattice specific heats and experimental data. As
, which seems appropriate to compare lattice specific heats and experimental data. As ![]() ranges typically between about 100 K (alkali metals) and 2000 K (diamond),
ranges typically between about 100 K (alkali metals) and 2000 K (diamond), ![]() corresponds to
corresponds to ![]() not greater than a few tens K degrees only; thus below
not greater than a few tens K degrees only; thus below ![]() the electron specific heat becomes comparable or predominant with respect to the mere lattice contribution.
the electron specific heat becomes comparable or predominant with respect to the mere lattice contribution.
The result reported in the Figure 2 shows that ![]() overlaps reasonably well the whole Debye curve, at least in the range of temperatures where the lattice specific heat alone realistically represents the experimental data. It appears in particular that even the
overlaps reasonably well the whole Debye curve, at least in the range of temperatures where the lattice specific heat alone realistically represents the experimental data. It appears in particular that even the ![]() dependence of lattice specific heat is correctly reproduced by the Equation (14) in the range
dependence of lattice specific heat is correctly reproduced by the Equation (14) in the range![]() , directly comparable with the experimental data:
, directly comparable with the experimental data: ![]() corresponds indeed to
corresponds indeed to ![]() of the order of about ten to hundred K degrees, where the lattice specific heat overcomes in general the electron contribution. The Figure 2 makes superfluous the direct comparison of the Equation (14) with the experimental data at
of the order of about ten to hundred K degrees, where the lattice specific heat overcomes in general the electron contribution. The Figure 2 makes superfluous the direct comparison of the Equation (14) with the experimental data at
![]()
Figure 2. Specific heats calculated from the Equation (14) (continuous line) and Debye (circle) Equation (10) vs![]() .
.
temperature range where the reliability of the Debye model is well acknowledged.
Note that this agreement does not represent a mere numerical result of best fit between the linear combination of three Einstein functions (6) and the Debye function, for at least four reasons:
1) since the Equation (15) is justifiable, see the next Equation (26), the Equation (13) express a specific physical idea, rather than fulfilling a mere numerical purpose;
2) the coefficients ![]() have not been calculated according to standard best fit algorithms;
have not been calculated according to standard best fit algorithms;
3) no “ad hoc” physical hypothesis has been purposely introduced to force this result, which has full theoretical character;
4) since the unique Einstein frequency waives the vibrational spectrum of the Debye model, the mere elaboration of the Equation (1) that yields (14) has in fact nothing to do with the elasticity theory.
Hence the conversion from the Equation (3) to the Debye-like Equation (8) cannot have numerical worth only, as it will be stressed in the next section. With these clarifications, the Equation (14) has its own self-contained physical meaning. The comparison with the Equation (10) has validation purpose only. The next section clarifies the reasons of this general agreement, while explaining also the small deviation between the curves observable in the Figure 2 at ![]() only: yet this deviation is still compatible with the experimental data in a region of temperatures where the total specific heat, experimentally measurable, is essentially controlled by the electron properties.
only: yet this deviation is still compatible with the experimental data in a region of temperatures where the total specific heat, experimentally measurable, is essentially controlled by the electron properties.
4. Discussion
The Equation (15) is definable in the frame of the present quantum model only, and not outside it e.g. via ancillary considerations involving classical hints. According to the Equation (13), one oscillator is actually an atom randomly delocalized in a crystal plane and vibrating normally to this plane: so, as expected, its zero point energy is direct consequence of its position uncertainty on one plane of the elementary cell. Consider that ![]() yields
yields![]() , being from a mere dimensional standpoint
, being from a mere dimensional standpoint![]() . Strictly speaking, however, is more appropriate to regard
. Strictly speaking, however, is more appropriate to regard ![]() for example as
for example as![]() , in which case the atom vibrates along the z direction. Actually the crystal plane defining the zero point energy is not rigidly fixed or uniquely definable; rather, the cyclic permutation of the indexes
, in which case the atom vibrates along the z direction. Actually the crystal plane defining the zero point energy is not rigidly fixed or uniquely definable; rather, the cyclic permutation of the indexes ![]() implies three delocalization chances on the planes
implies three delocalization chances on the planes![]() ,
, ![]() and
and ![]() and corresponding orthogonal vibration directions, in agreement with the fact that the number of oscillators is three times that of the atoms. Moreover, as the three planes describe in fact the lattice volume of the elementary cell, the zero point energy fulfills both properties inherent its quantum nature: on the one hand it is naturally associated to the vibrational energy of the propagating wave, in agreement with the standard description of the quantum oscillators; on the other hand it also appears as expected consequence of the confinement of any particle in a volume of space, whose size is defined by the distance between neighbor atoms consistently with the lattice parameters of the elementary cell.
and corresponding orthogonal vibration directions, in agreement with the fact that the number of oscillators is three times that of the atoms. Moreover, as the three planes describe in fact the lattice volume of the elementary cell, the zero point energy fulfills both properties inherent its quantum nature: on the one hand it is naturally associated to the vibrational energy of the propagating wave, in agreement with the standard description of the quantum oscillators; on the other hand it also appears as expected consequence of the confinement of any particle in a volume of space, whose size is defined by the distance between neighbor atoms consistently with the lattice parameters of the elementary cell.
Four remarks summarize the present outcomes.
-The Equation (14) has general validity: no specific hypothesis about the kind of material has been introduced; the features of the lattice oscillator are defined by three ![]() only, in order to account for its zero point energy and ground vibrational level regardless of the specific kind of atom.
only, in order to account for its zero point energy and ground vibrational level regardless of the specific kind of atom.
-The conversion of the plain Equation (3) into the form (8) does not require assuming a continuous body of matter and does not involve thermodynamic quantities, like for example the compressibility, which are unnecessary and bypassed.
-The Debye-like formula (14) has full quantum meaning, without reference to classical concepts; rather, reverting the conceptual path of Debye, it is possible to infer as a corollary of this equation his background considerations about elastic constants of the material and vibrational spectrum. In effect the position (15) yields![]() , as it appears comparing the Equations (15) and (16).
, as it appears comparing the Equations (15) and (16).
-The Figure 2 does not require the detailed analysis about the longitudinal or transversal character of the lattice waves nor about the microscopic interaction mechanism between atoms introduced by the Equation (4); it is enough to admit that the coupling of lattice oscillators is induced by propagating the perturbation of one trigger atom, in turn due to its position uncertainty in the lattice site.
The next considerations of this section highlight further these positions.
The Debye approach refined the early Einstein model of specific heat at the conceptual cost of several approximations, first of all postulating an upper cutoff frequency ![]() to bypass the consequence of an infinite number of proper oscillations in principle admissible in a continuous body of matter. Clearly the key assumption of “continuum” is senseless for high frequencies, whose vibrational wavelengths are so short to be smaller than or comparable with the crystal spacing of atom lattice; also, the
to bypass the consequence of an infinite number of proper oscillations in principle admissible in a continuous body of matter. Clearly the key assumption of “continuum” is senseless for high frequencies, whose vibrational wavelengths are so short to be smaller than or comparable with the crystal spacing of atom lattice; also, the ![]() spectrum is sensible for low vibrational frequencies only, i.e. whose wavelengths are so extended to involve several atoms. Eventually, the lower integration limit
spectrum is sensible for low vibrational frequencies only, i.e. whose wavelengths are so extended to involve several atoms. Eventually, the lower integration limit ![]() is of course a numerical extrapolation rather than a real physical value. Yet the successful intuition of Debye was that just these low energy waves that overcome the interatomic distances in the lattice are related to the elastic properties of solids: at low
is of course a numerical extrapolation rather than a real physical value. Yet the successful intuition of Debye was that just these low energy waves that overcome the interatomic distances in the lattice are related to the elastic properties of solids: at low ![]() the density of spectral lines described by the frequency distribution function is a satisfactory approximation. This point, well discussed in the Debye original paper, is shortly reappraised here considering the amount
the density of spectral lines described by the frequency distribution function is a satisfactory approximation. This point, well discussed in the Debye original paper, is shortly reappraised here considering the amount ![]() of matter contained in a volume of lattice given by
of matter contained in a volume of lattice given by
![]() (17)
(17)
The notation emphasizes that the lattice volume defined in this way is just that including all atoms oscillating with wavelengths![]() , i.e. it is the volume including coupled oscillators. As previously highlighted, the wavelengths are reasonably related to the lattice parameters of the elementary cell via the respective average velocities
, i.e. it is the volume including coupled oscillators. As previously highlighted, the wavelengths are reasonably related to the lattice parameters of the elementary cell via the respective average velocities ![]() describing the displacement rate of atoms around the equilibrium lattice sites;
describing the displacement rate of atoms around the equilibrium lattice sites; ![]() is an appropriate proportionality factor added for sake of generality. If, for example,
is an appropriate proportionality factor added for sake of generality. If, for example, ![]() is defined by the product of three integers
is defined by the product of three integers
![]()
then one obtains two equations
![]() (18)
(18)
In the second equation, ![]() are the shortest lengths that repeated
are the shortest lengths that repeated ![]() times repro- duce the
times repro- duce the ![]() periodicity; these positions account for the actual extent of
periodicity; these positions account for the actual extent of ![]() via the arbitrary
via the arbitrary![]() , as in fact
, as in fact ![]() whatever
whatever ![]() might actually be. This suggests that
might actually be. This suggests that ![]() are elementary cell parameters and that the largest one among the three ratios
are elementary cell parameters and that the largest one among the three ratios ![]() is identifiable with the Debye cutoff
is identifiable with the Debye cutoff![]() , which here appears in a natural way. In the Debye model
, which here appears in a natural way. In the Debye model ![]() (with Author’s notation) defines the number of proper frequencies below the upper threshold
(with Author’s notation) defines the number of proper frequencies below the upper threshold ![]() via the function
via the function ![]() of elasticity constants and density
of elasticity constants and density![]() : in effect, putting
: in effect, putting ![]() because
because ![]() has physical dimensions
has physical dimensions ![]() and normalizing
and normalizing ![]() to
to ![]() for
for![]() , the first Equation (18) yields
, the first Equation (18) yields![]() . This check supports the validity of the Equation (17).
. This check supports the validity of the Equation (17).
In the Equation (17) the vibrational wavelengths determine the size of![]() , which therefore defines the local density
, which therefore defines the local density ![]() and energy density
and energy density ![]() due to all lattice oscillators involved by the extent of
due to all lattice oscillators involved by the extent of![]() . So
. So ![]() represents the size of the coupling volume. Let be then
represents the size of the coupling volume. Let be then
![]() (19)
(19)
being ![]() the total mass in
the total mass in ![]() and
and ![]() the average square velocity of vibrational displacement of lattice atoms in the coupling volume;
the average square velocity of vibrational displacement of lattice atoms in the coupling volume; ![]() takes into account the virial theorem, whereas
takes into account the virial theorem, whereas ![]() links these considerations to the lattice
links these considerations to the lattice![]() . Note now that
. Note now that ![]() has physical dimensions of reciprocal velocity, so that the energy density can be rewritten as
has physical dimensions of reciprocal velocity, so that the energy density can be rewritten as
![]()
Moreover, putting ![]() in the Equation (18), one finds
in the Equation (18), one finds
![]()
which implies that ![]() must be finite. Eventually, since the energy density per unit volume of solid is by definition proportional to the number of oscillators contained in
must be finite. Eventually, since the energy density per unit volume of solid is by definition proportional to the number of oscillators contained in![]() , which is in turn representative of the amount of oscillating mass and thus related to
, which is in turn representative of the amount of oscillating mass and thus related to![]() , the lattice energy is
, the lattice energy is
![]() (20)
(20)
As expected, specific properties of the material appear in![]() ; thus, whatever
; thus, whatever ![]() might be,
might be,
![]() (21)
(21)
being ![]() according to the Equations (13). Clearly
according to the Equations (13). Clearly ![]() is the frequency range around the average value
is the frequency range around the average value ![]() to which is related, at the first order, the given interval
to which is related, at the first order, the given interval ![]() of local lattice energy.
of local lattice energy.
The Equation (21) is crucial to explain the Figure 2: assuming that the former addend is negligible with respect to the second one, i.e. if ![]() is approximately independent of
is approximately independent of ![]() or even constant, then
or even constant, then ![]() reduces to the form of the integrand in the Equation (9). In effect the frequency spectrum
reduces to the form of the integrand in the Equation (9). In effect the frequency spectrum![]() , here regarded as
, here regarded as![]() , agrees with that of the Debye model, but implies that the dynamics of lattice atoms is approximately independent of the average wave frequency. This is intuitively reasonable only for vibrational wavelengths comparable or small enough with respect to the lattice parameters, when in effect the interaction between neighbor atoms in contiguous lattice sites becomes negligible; the fact that in this case
, agrees with that of the Debye model, but implies that the dynamics of lattice atoms is approximately independent of the average wave frequency. This is intuitively reasonable only for vibrational wavelengths comparable or small enough with respect to the lattice parameters, when in effect the interaction between neighbor atoms in contiguous lattice sites becomes negligible; the fact that in this case ![]() concerns independent Einstein oscillators explains why at high
concerns independent Einstein oscillators explains why at high ![]() the curves
the curves ![]() and
and ![]() tend to merge into the unique classical limit. In effect the most significant deviation of the Einstein curve with respect to the Debye curve is at low
tend to merge into the unique classical limit. In effect the most significant deviation of the Einstein curve with respect to the Debye curve is at low![]() , when the low vibrational energies become significant: as previously emphasized, long range wavelengths necessarily imply by definition coupled oscillators. This appears in the Equation (17): on the one hand
, when the low vibrational energies become significant: as previously emphasized, long range wavelengths necessarily imply by definition coupled oscillators. This appears in the Equation (17): on the one hand ![]() decreases at increasing
decreases at increasing![]() , i.e.
, i.e.![]() , until its size is of the order of the volume of the elementary cell, on the other hand
, until its size is of the order of the volume of the elementary cell, on the other hand ![]() corresponds just for this reason to this minimum value of
corresponds just for this reason to this minimum value of![]() .
.
The lattice energy was implemented by Debye via the number ![]() of oscillators with a given frequency inferred from the elasticity theory, as previously found in the Equation (18); normalizing then
of oscillators with a given frequency inferred from the elasticity theory, as previously found in the Equation (18); normalizing then![]() , with
, with ![]() Debye calculates
Debye calculates![]() . So the unique
. So the unique ![]() of Einstein turns into
of Einstein turns into ![]() times the Bose function, to be integrated between
times the Bose function, to be integrated between ![]() and
and![]() . However
. However ![]() not necessarily constant stimulates comparing the approximations of
not necessarily constant stimulates comparing the approximations of ![]() either with
either with ![]() only or with
only or with ![]() only; this last term can be calculated knowing the function
only; this last term can be calculated knowing the function![]() . Accordingly, once normalizing again
. Accordingly, once normalizing again![]() , the lattice energy distribution that weights the Einstein unique frequency implements now the approximation
, the lattice energy distribution that weights the Einstein unique frequency implements now the approximation ![]() alternative to that of Debye. In principle, when significant deviations from the
alternative to that of Debye. In principle, when significant deviations from the ![]() law are expected, the first addend of the Equation (21) should provide the appropriate correction to the approximate Debye spectrum. As actually is realistically expectable in general a concurrent contribution of both terms, these considerations explain the small discrepancy between
law are expected, the first addend of the Equation (21) should provide the appropriate correction to the approximate Debye spectrum. As actually is realistically expectable in general a concurrent contribution of both terms, these considerations explain the small discrepancy between ![]() and
and ![]() visible in the Figure 2 at very low values of
visible in the Figure 2 at very low values of![]() , where however in most cases the lattice specific heat alone does not represent the experimental specific heat, e.g. in metals.
, where however in most cases the lattice specific heat alone does not represent the experimental specific heat, e.g. in metals.
Approaching quantitatively this kind of problem requires details about the thermodynamics of matter: this topic, inherent![]() , leads to the domain remarkably explored by the Debye and Born-von Karman models. In effect, further physical information is necessary on
, leads to the domain remarkably explored by the Debye and Born-von Karman models. In effect, further physical information is necessary on ![]() to assess separately the two addends of the Equation (21) and understand when the first one is actually negligible with respect to the second one.
to assess separately the two addends of the Equation (21) and understand when the first one is actually negligible with respect to the second one.
To this aim put![]() , where
, where ![]() could be for example the series expansion of an unknown function
could be for example the series expansion of an unknown function ![]() whose zero order term is just
whose zero order term is just![]() . Whatever the analytical form of
. Whatever the analytical form of ![]() might be, the Equations (20) and (21) yield
might be, the Equations (20) and (21) yield
![]()
being ![]() the integration constant; thus
the integration constant; thus
![]()
The addends of the Equation (21) are now compared to understand in particular when
![]() (22)
(22)
since both inequalities are in principle possible. The first inequality reads
![]()
The comparison is immediate considering preliminarily, for simplicity of notation only, ![]() at the first order, i.e. putting
at the first order, i.e. putting![]() ; so
; so
![]()
Put now purposely![]() , being
, being ![]() an arbitrary constant value among those allowed for
an arbitrary constant value among those allowed for![]() ; with this value of
; with this value of ![]() the left hand side of the inequality is by definition close to zero for
the left hand side of the inequality is by definition close to zero for![]() , whereas the right hand side reads
, whereas the right hand side reads
![]()
i.e. it remains finite even at![]() . This shows that in an appropriate range of
. This shows that in an appropriate range of ![]() around the fixed
around the fixed ![]() the finite value
the finite value ![]() overcomes the vanishing value at the left hand side, thus fulfilling the first inequality (22). It is also evident that this reasoning holds in principle even considering all series terms of the function
overcomes the vanishing value at the left hand side, thus fulfilling the first inequality (22). It is also evident that this reasoning holds in principle even considering all series terms of the function![]() . The reasonable conclusion is that the inequality representing the Debye spectrum approximation is actually fulfilled in a well-defined range of frequencies only, in particular at low
. The reasonable conclusion is that the inequality representing the Debye spectrum approximation is actually fulfilled in a well-defined range of frequencies only, in particular at low ![]() where
where ![]() is expectedly small. The notation
is expectedly small. The notation ![]() emphasizes this chance. Moreover, repeating exactly this reasoning, one finds that the second inequality (22) holds in a range of
emphasizes this chance. Moreover, repeating exactly this reasoning, one finds that the second inequality (22) holds in a range of ![]() around a new frequency
around a new frequency![]() : the idea is still to define
: the idea is still to define ![]() as that where the right hand side vanishes, but not the left hand side. Hence around the boundaries of the range
as that where the right hand side vanishes, but not the left hand side. Hence around the boundaries of the range ![]() allowed to
allowed to![]() , the frequency spectrum is governed by
, the frequency spectrum is governed by ![]() or by the familiar
or by the familiar![]() . Strictly speaking, therefore, the approximation
. Strictly speaking, therefore, the approximation ![]() is legitimate only in a small range of frequencies
is legitimate only in a small range of frequencies ![]() around
around ![]() that defines
that defines![]() . Unfortunately Debye did not find both alternatives because of his classical way to infer the
. Unfortunately Debye did not find both alternatives because of his classical way to infer the ![]() law via the elasticity theory, while acknowledging however its inherent approximate character. All this implies that the
law via the elasticity theory, while acknowledging however its inherent approximate character. All this implies that the ![]() dependence of the specific heat is to be expected only in the range of temperatures where holds the Debye spectrum; in the range of temperatures where prevails the
dependence of the specific heat is to be expected only in the range of temperatures where holds the Debye spectrum; in the range of temperatures where prevails the ![]() frequency spectrum, however, the
frequency spectrum, however, the ![]() law does not hold. The Figure 2 agrees with the idea that this law is actually not extensible down to the absolute zero.
law does not hold. The Figure 2 agrees with the idea that this law is actually not extensible down to the absolute zero.
Nevertheless the Debye approach, as it is, represents valuable enhancement of the early Einstein mode, particularly significant at low![]() ; its acknowledged accuracy represents therefore reliable reference to assess the physical significance of the steps from the Equations (3) to (8).
; its acknowledged accuracy represents therefore reliable reference to assess the physical significance of the steps from the Equations (3) to (8).
As concerns the Equation (15), regard the second addend of the Equation (21) as ![]() only; introducing it in the Equation (1), including
only; introducing it in the Equation (1), including ![]() into
into ![]() and then integrating as done in the Equation (9) means just replicating the Debye approach, for which holds therefore the second Equation (11). This is indeed an obvious condition to overlap successfully the Equations (9) and (14). Next, solving
and then integrating as done in the Equation (9) means just replicating the Debye approach, for which holds therefore the second Equation (11). This is indeed an obvious condition to overlap successfully the Equations (9) and (14). Next, solving ![]() at
at ![]() with respect to
with respect to![]() , which is now the only unknown once having calculated
, which is now the only unknown once having calculated![]() , one finds that
, one finds that ![]() is of course just that of the Equation (15): indeed just this latter yields the Equation (16).
is of course just that of the Equation (15): indeed just this latter yields the Equation (16).
Despite these steps from (17) to (21) do not involve classical hints, this way to infer the Equation (15) is however indirect: it requires implementing the link just exposed of the Equation (14) with the Debye Equation (10), and is thus unsatisfactory. Below, a more fundamental way is proposed to show that the physical background of the second Equation (11) has full quantum base directly related to the Equation (13) regardless of the frequency distribution spectrum: in this way the Equation (15) shows its inherent physical meaning, rather than being mere numerical result of calculations.
To describe how the lattice atom interacts with the neighbors, let us introduce its momentum transferred towards an arbitrary surface surrounding the equilibrium lattice site: the momentum exchanged with neighbor atoms accounts for its coupling and shows that the ratio ![]() of the Equations (12) and (13) is related just to the concept of coupling process. According to the Equations (17) and (18), let
of the Equations (12) and (13) is related just to the concept of coupling process. According to the Equations (17) and (18), let ![]() be the average displacement velocity of an atom oscillating around its equilibrium position and
be the average displacement velocity of an atom oscillating around its equilibrium position and ![]() its average momentum; i.e. the components of
its average momentum; i.e. the components of ![]() are that previously introduced to define
are that previously introduced to define ![]() of the Equation (19). Also, consider the surface element
of the Equation (19). Also, consider the surface element ![]() around the equilibrium site; the local unit vector
around the equilibrium site; the local unit vector ![]() is oriented outwards normally to the local surface. As
is oriented outwards normally to the local surface. As ![]() reads
reads![]() , dividing both sides by
, dividing both sides by ![]() one finds that
one finds that ![]() yields
yields
![]() (23)
(23)
The left hand side of the first equation defines the element of solid angle![]() ; the right hand side reads
; the right hand side reads![]() . Put by dimensional reasons
. Put by dimensional reasons![]() , being
, being ![]() an arbitrary length function of
an arbitrary length function of ![]() and
and ![]() a frequency that by definition does not depend upon
a frequency that by definition does not depend upon![]() , as instead
, as instead ![]() does by reasons that will appear just below. Therefore the first Equation (23) yields
does by reasons that will appear just below. Therefore the first Equation (23) yields
![]()
These positions are possible because all related quantities are arbitrary. Integrating both sides, one finds![]() . The reasonable conclusion is
. The reasonable conclusion is
![]()
indeed if ![]() would be constant, then
would be constant, then![]() . Let us rewrite the last equation as
. Let us rewrite the last equation as
![]() (24)
(24)
At this point, let us try to plug ![]() in the frame of the model hitherto formulated; the fact that it is arbitrary, and thus purposely definable, avoids the difficulty of regarding it as new frequency hardly explainable in the present frame. Accordingly, link this result with
in the frame of the model hitherto formulated; the fact that it is arbitrary, and thus purposely definable, avoids the difficulty of regarding it as new frequency hardly explainable in the present frame. Accordingly, link this result with ![]() of the Equation (14), of interest for the present purposes and expected recalling the form of the Equation (13). Let be at the inflexion point of the curve
of the Equation (14), of interest for the present purposes and expected recalling the form of the Equation (13). Let be at the inflexion point of the curve ![]() vs
vs ![]()
![]() (25)
(25)
in effect ![]() is just the value of the second Equation (11), whereas the second position follows thinking that in general the zero point energy
is just the value of the second Equation (11), whereas the second position follows thinking that in general the zero point energy ![]() is merely due to the random delocalization of any particle confined in a region of space. As
is merely due to the random delocalization of any particle confined in a region of space. As ![]() and
and ![]() are related to the propagation directions of the respective waves, according to the Equation (12) one concludes that
are related to the propagation directions of the respective waves, according to the Equation (12) one concludes that ![]() is the only frequency consistent with the property
is the only frequency consistent with the property![]() . So the Equation (24) reads
. So the Equation (24) reads
![]() (26)
(26)
whence
![]()
the value of ![]() results to be just that previously introduced in the Equation (15). This shows that in effect both positions (25) fit
results to be just that previously introduced in the Equation (15). This shows that in effect both positions (25) fit ![]() and
and ![]() to the three vibrational and zero point
to the three vibrational and zero point ![]() (13) without introducing further frequencies. Moreover note that in general
(13) without introducing further frequencies. Moreover note that in general![]() , with
, with ![]() and
and ![]() defined in the Equation (23); hence the Equation (26) reads
defined in the Equation (23); hence the Equation (26) reads
![]()
if![]() , then
, then ![]() would yield
would yield![]() ; the fact that actually
; the fact that actually ![]() shows that the momentum
shows that the momentum ![]() is not uniformly transferred all around the oscillating atom. This is reasonable: the interaction driven coupling preferentially points towards specific lattice directions where other atoms are found to which the vibrational momentum is effectively transferred. So the integration of momentum transfer across the surface element defined by
is not uniformly transferred all around the oscillating atom. This is reasonable: the interaction driven coupling preferentially points towards specific lattice directions where other atoms are found to which the vibrational momentum is effectively transferred. So the integration of momentum transfer across the surface element defined by ![]() is smaller than that expected for a continuous solid or amorphous microstructure.
is smaller than that expected for a continuous solid or amorphous microstructure.
At this point integrating at constant volume it is possible to find the lattice internal energy![]() , i.e.
, i.e.
![]()
and entropy![]() , i.e.
, i.e.
![]()
from which one calculates the Helmholtz lattice free energy![]() .
.
As a closing remark, note that at very low ![]() the Equation (14) can be also rewritten thinking one vibration wave only and two zero point terms; in other words, it is also physically admissible the following formula of specific heat, obtained simply moving the coefficient 2 from the second to the first addend,
the Equation (14) can be also rewritten thinking one vibration wave only and two zero point terms; in other words, it is also physically admissible the following formula of specific heat, obtained simply moving the coefficient 2 from the second to the first addend,
![]()
to which are related the energy
![]()
and entropy
![]()
The notation reflects preliminary indications, according which these quantities could be related to the superfluid state, of course with different ![]() and
and ![]() and
and![]() . Further investigation is in progress on this possible implication of the present model.
. Further investigation is in progress on this possible implication of the present model.
5. Further Implications of the Present Model
The main purpose of the present paper was to highlight that the Einstein and Debye approaches are directly correlated when accounting appropriately for the zero point energy of the crystal lattice: the Equation (5) describes the thermal oscillators of the lattice introducing the Einstein initial Equation (1) as a straightforward consequence of the Bose statistics and allows to infer the Debye-like Equation (14) calculable as a function of![]() . Yet a similar kind of approach, owing to its generality, should be in principle adequate to describe even a system of fermions, for example the free electron gas in the lattice. Indeed this section shows that to this purpose it is enough to start from
. Yet a similar kind of approach, owing to its generality, should be in principle adequate to describe even a system of fermions, for example the free electron gas in the lattice. Indeed this section shows that to this purpose it is enough to start from
![]() (27)
(27)
with the same physical meaning of degeneracy factor ![]() and still with the unique frequency
and still with the unique frequency![]() . Besides the intrinsic importance of this topic, the following considerations are significant to confirm further the validity of the steps leading from the Equation (1) to the Equation (5). In fact the extension proposed here of the present approach implies merely finding how the physical differences between either statistical distribution compel reformulating the Equations (6) to (8) once having replaced the Equation (1) with the Equation (27). Let us rewrite first the Equation (5) with the same notations as
. Besides the intrinsic importance of this topic, the following considerations are significant to confirm further the validity of the steps leading from the Equation (1) to the Equation (5). In fact the extension proposed here of the present approach implies merely finding how the physical differences between either statistical distribution compel reformulating the Equations (6) to (8) once having replaced the Equation (1) with the Equation (27). Let us rewrite first the Equation (5) with the same notations as
![]() (28)
(28)
Now the limit value of ![]() for
for ![]() is different from
is different from![]() ; so, without chance of obtaining this limit case, is also missing the necessity of
; so, without chance of obtaining this limit case, is also missing the necessity of ![]() and thus
and thus![]() . Furthermore fails also the idea of replacing
. Furthermore fails also the idea of replacing ![]() with a unique
with a unique![]() , as the three waves must be in different quantum states: this of course implies different
, as the three waves must be in different quantum states: this of course implies different![]() . Instead still holds the idea of equivalence of the three space directions along which is transmitted the interaction between particles; it is irrelevant in this respect that, actually, in this case the Coulomb electron interaction replaces vibrational interaction of lattice oscillators. While expecting reasonably equal
. Instead still holds the idea of equivalence of the three space directions along which is transmitted the interaction between particles; it is irrelevant in this respect that, actually, in this case the Coulomb electron interaction replaces vibrational interaction of lattice oscillators. While expecting reasonably equal![]() , whose unique value is expressed now with the notation
, whose unique value is expressed now with the notation![]() , in general
, in general![]() ; should hold by consequence the position
; should hold by consequence the position
![]()
As ![]() is no longer a constant, it can be nothing else but a function of the only quantity,
is no longer a constant, it can be nothing else but a function of the only quantity, ![]() , that does not depend on the index
, that does not depend on the index![]() . So
. So
![]() (29)
(29)
owing to the coefficient![]() , appear in the Equation (28) both
, appear in the Equation (28) both ![]() and
and![]() . It is interesting the fact that
. It is interesting the fact that ![]() yields
yields ![]() with
with![]() ; i.e. even the effective number of oscillators is changed with respect to the initial
; i.e. even the effective number of oscillators is changed with respect to the initial![]() . Nevertheless the primed and unprimed quantities are correlated, the correlation function being just
. Nevertheless the primed and unprimed quantities are correlated, the correlation function being just![]() . Let be therefore
. Let be therefore
![]() (30)
(30)
and then
![]() (31)
(31)
The form of the function ![]() must fulfill three boundary conditions:
must fulfill three boundary conditions:
1) the limit ![]() of
of ![]() for
for ![]() cannot be zero, because of the zero point energy;
cannot be zero, because of the zero point energy;
2) the limit ![]() of
of ![]() for
for ![]() must be zero;
must be zero;
3) the limit ![]() of
of ![]() for
for ![]() must not diverge.
must not diverge.
Owing to the terms ![]() at denominator, the Equation (30) requires
at denominator, the Equation (30) requires
![]() (32)
(32)
in order that
![]() (33)
(33)
The reason of having introduced in the Equation (32) the smallest one among the three ![]() is coherent with the chance of defining uniquely
is coherent with the chance of defining uniquely ![]() independently of the index
independently of the index![]() ; so, for
; so, for ![]() in one term only of the sum the ratio
in one term only of the sum the ratio ![]() is different from zero, whereas the remaining two vanish according to
is different from zero, whereas the remaining two vanish according to![]() . Also now one wave accounts for the zero point energy. Hence
. Also now one wave accounts for the zero point energy. Hence
![]() (34)
(34)
owing to the positions (32), this is a minimum zero point energy; hence ![]() does not vanish at
does not vanish at![]() . It is formally convenient now to express
. It is formally convenient now to express
![]()
being ![]() and
and ![]() multiplicative proportionality constants to express
multiplicative proportionality constants to express ![]() and
and![]() ; both constants are by definition
; both constants are by definition ![]() according to the Equation (32). So the first Equation (34) reads explicitly
according to the Equation (32). So the first Equation (34) reads explicitly
![]() (35)
(35)
whereas ![]() follows by consequence.
follows by consequence.
Despite the function ![]() is still unknown, let us express it through its series expansion
is still unknown, let us express it through its series expansion![]() , via appropriate coefficients
, via appropriate coefficients ![]() of the series. Now let us account for the three boundary conditions. It is clear that the highest power cannot be
of the series. Now let us account for the three boundary conditions. It is clear that the highest power cannot be![]() , otherwise
, otherwise ![]() in the second addend of the Equation (31) would diverge with
in the second addend of the Equation (31) would diverge with![]() . Since the power up to
. Since the power up to ![]() is in principle admissible, we have three chances to check. Trivial calculations yield:
is in principle admissible, we have three chances to check. Trivial calculations yield:
![]()
![]()
![]()
Owing to the zero order coefficient![]() , the zero point energy is correct in all cases. The first case yields sensible
, the zero point energy is correct in all cases. The first case yields sensible ![]() but wrong
but wrong![]() . In the third case holds exactly the contrary. In the second case both limits are wrong. As the term
. In the third case holds exactly the contrary. In the second case both limits are wrong. As the term ![]() only accounts well for
only accounts well for ![]() at low temperatures, whereas
at low temperatures, whereas ![]() only accounts well for its high temperature limit, these results suggest that the correct form of
only accounts well for its high temperature limit, these results suggest that the correct form of ![]() is the one that interpolates appropriately both chances:
is the one that interpolates appropriately both chances:
![]()
In conclusion, replacing just the last form of ![]() in the Equation (35) and deriving with respect to
in the Equation (35) and deriving with respect to![]() , one should find the correct form of
, one should find the correct form of ![]() and thus of
and thus of![]() . This formula is not quoted explicitly for brevity. To check this conclusion in a crucial case, i.e. at low
. This formula is not quoted explicitly for brevity. To check this conclusion in a crucial case, i.e. at low![]() , it is enough to expand in series this
, it is enough to expand in series this ![]() calculated from the Equation (35), taking advantage of the fact that the limits for
calculated from the Equation (35), taking advantage of the fact that the limits for ![]() of
of ![]() and
and
![]() around
around ![]() are in fact finite in the present model: i.e.
are in fact finite in the present model: i.e.
![]() and
and![]() . The result is thus
. The result is thus
![]() (36)
(36)
where the constant ![]() plays the role of reduced temperature. In conclusion, the Fermi statistics compels at the first order the linear
plays the role of reduced temperature. In conclusion, the Fermi statistics compels at the first order the linear ![]() dependence of the specific heat, as it is known.
dependence of the specific heat, as it is known.
Of course several considerations are possible about how the constants appearing in this expression are related to the physical properties of metals. However these considerations, going back to Fermi’s time, are omitted here for brevity: the purpose of this extension is simply to demonstrate that the Equation (27) only is inherently enough to obtain the well known Equation (36), likewise as the Equation (1) only is inherently enough to obtain the well known Debye-like Equation (14).
6. Conclusions
Unfortunately neither Einstein nor Debye realized that actually their theoretical models coincide merely handling appropriately a unique lattice frequency, even without need of implementing the classical theory of elasticity.
In this respect, the key point to improve the early Einstein result is not the frequency distribution spectrum ![]() but the quantum zero point energy, being actually the former, a consequence of the latter.
but the quantum zero point energy, being actually the former, a consequence of the latter.
The conceptual basis of all Debye considerations and its implications on the link between thermodynamic and elastic properties of solids have actually full quantum origin, once regarding the latter as a mere corollary of the Equation (14).
The Equations (5) and (6) are easily generalizable to the case of a system of fermions.
Eventually it is noted that the model is easily generalizable to describe phenomena like the superfluidity as well, simply admitting that in the case of a fluid ![]() of the Equation (15) is not necessarily a constant; more specifically, the Equation (14) shows that if
of the Equation (15) is not necessarily a constant; more specifically, the Equation (14) shows that if ![]() decreases then
decreases then ![]() increases. If a good physical reason exists to demonstrate that
increases. If a good physical reason exists to demonstrate that ![]() is allowed to decrease at an appropriate value of
is allowed to decrease at an appropriate value of![]() , then simple calculations show that at this particular
, then simple calculations show that at this particular ![]() the Equation (14) is in fact compatible with the analytical form of the so called
the Equation (14) is in fact compatible with the analytical form of the so called ![]() -point. In principle this conclusion is physically expectable in the present model without additional hypotheses; it simply follows from the chance of defining the transition between a thermodynamic state with energy and entropy
-point. In principle this conclusion is physically expectable in the present model without additional hypotheses; it simply follows from the chance of defining the transition between a thermodynamic state with energy and entropy ![]() and
and ![]() to another state characterized by
to another state characterized by ![]() and
and![]() . Accordingly, just the change of zero point energy and vibrational wave energy consistent with either chance of regarding the components of the position (4) could be the key concept to describe the low
. Accordingly, just the change of zero point energy and vibrational wave energy consistent with either chance of regarding the components of the position (4) could be the key concept to describe the low ![]() behavior of
behavior of ![]() and
and![]() , of course in agreement with the vanishing of both
, of course in agreement with the vanishing of both ![]() and
and ![]() at the absolute zero. Activity is in advanced progress on this topic.
at the absolute zero. Activity is in advanced progress on this topic.
NOTES
![]()
*Retired physicist.