Compressed Sensing Based on the Single Layer Wavelet Transform for Image Fusion ()
1. Introduction
Image fusion is the technique that integrates complementary and redundant information of multiple images to obtain a composite one, which contains more comprehensive description than any of the individual image. As a result of the processing, the fused image is more useful for human and machine perception or further image processing tasks such as object detection and recognition. By now, many well-known fusion algorithms have been proposed [1]. And the most popular technique up to now is multi- resolution decomposition methods, such as pyramid-based methods [2], discrete wavelet transform (DWT)-based methods [3] etc. But most of them need the whole acquisition of the source images, which means that the large of storage burden must be handled especially due to the growing sensor data volumes.
In recent years, a new technique for simultaneous data sampling and compression known as compressive sensing (CS) [4] [5] [6] [7] has been developed. It builds upon the ground breaking work by Donoho [7] and Candes et al. [8], who showed that under certain conditions, a signal can be precisely recovered from only a small set of measurements. The CS principle provides the potential of dramatic reduction of sampling rates, power consumption and computation complexity in digital data acquisitions. Due to its great practical potentials, it has caused great interest both in academia and industries in the past few years [9] [10]. However, most of existing works in CS remain at the theoretical research.
For image fusion in CS, one natural way is to perform traditional fusion among the reconstructed multiple images after separate recover of each image from the measurements. However, in order to save storage space and reduce the computational complexity, a better method is to directly perform fusion on the measurements, and then to reconstruct the fused image from the fused measurements. Recently, several different fusion strategy based on CS which have been proposed, e.g., a simple maximum selection rule [11] or a self adaptive weighted average fusion scheme based on standard deviation of measurements [12].
In this paper, we proposed an image fusion scheme in a general CS framework. Specifically, we just take single layer wavelet decomposition for image and only measured the high-pass wavelet coefficients of the image with Fast Walsh Hadamard Transform [13], then, fused the low-pass wavelet coefficients and the measurements of high-pass wavelet coefficients with different schemes. The composite coefficients of the fused image are subsequently recovered via the total variation optimization (TV) algorithm [14] and inverse wavelet transform.
This paper is organized as follows. In Section 1, we provide a brief review of CS. The proposed fusion scheme based on CS is described in Section 3. Some experimental results and a discussion are given in Section 4. Finally, Section 5 ends this paper with a conclusion.
2. Overview of Compressive Sensing
Consider a real-valued, finite-length, one-dimensional, discrete-time signal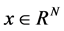 , with elements
, with elements 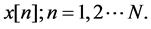 We say that the signal x is K sparse if it can be represented as:
We say that the signal x is K sparse if it can be represented as:
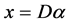 (1)
(1)
where 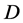 is an
is an 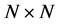 basis matrix and
basis matrix and 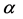 is an
is an 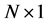 vector containing only K nonzero coefficients. Clearly, x and
vector containing only K nonzero coefficients. Clearly, x and 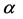 are equivalent representations of the signal, with x in the time or space domain and
are equivalent representations of the signal, with x in the time or space domain and 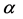 in the
in the 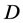 domain. If
domain. If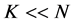 , the signal x is compressible.
, the signal x is compressible.
In CS, we can not measure or encode 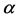 directly, rather, we take the compressive measurements:
directly, rather, we take the compressive measurements:
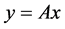 (2)
(2)
where 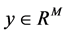 and
and 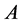 is an
is an 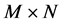 measurement matrix representing the measurement process. Since
measurement matrix representing the measurement process. Since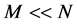 , the reconstruction of x from y is generally ill-posed. However, the CS theory is based on the fact that x has a sparse representation in a known transform domain
, the reconstruction of x from y is generally ill-posed. However, the CS theory is based on the fact that x has a sparse representation in a known transform domain  (e.g., the DCT and the wavelet). In other words, the transform domain signal
(e.g., the DCT and the wavelet). In other words, the transform domain signal ![]() can be recovered perfectly using an optimisation process if
can be recovered perfectly using an optimisation process if ![]() satisfies the restricted isometry property (RIP) [8]. Under some fixed sparsifying basis
satisfies the restricted isometry property (RIP) [8]. Under some fixed sparsifying basis![]() , such as Gaussian or Bernoulli i.i.d matrices offer universality and optimal performance as measurement matrices [7] [8], but with a high computational complexity. A new sampling operator called Fast Walsh Hadamard Transform [14] is also quite universal but with a lower complexity.
, such as Gaussian or Bernoulli i.i.d matrices offer universality and optimal performance as measurement matrices [7] [8], but with a high computational complexity. A new sampling operator called Fast Walsh Hadamard Transform [14] is also quite universal but with a lower complexity.
To solve the inverse transform from Equation (2), some non-linear recovery algorithms for such ill-posed problems have been developed [4] [5]-[10]. Unfortunately, most of them require fairly heavy computations in practice. In this paper ,we use a new efficient TV minimization scheme based on augmented Lagrangian and alternating direction algorithms, short for “TVAL3 scheme” to solve the problem[14]. It is presented for solving the compressive sensing problem with total variation regularization:
![]() (3)
(3)
where x is an ![]() vector,
vector, ![]() is the discrete gradient of x at pixel i,
is the discrete gradient of x at pixel i, ![]() is an
is an ![]() (M < N) measurement matrix, and measurements y are the linear projection of x.
(M < N) measurement matrix, and measurements y are the linear projection of x. ![]() is 1-norm(corresponding to the anisotropic TV).
is 1-norm(corresponding to the anisotropic TV).
3. The Proposed Scheme
3.1. Sampling
In order to obtain the measurements of the original images, a type of structured measurement matrices called Fast Walsh Hadamard Transform matrices will be used [14]. The measurement matrices are able to handle the fast computation of matrix-vector multiplication. It is constructed by the Hadamard Matrix. The Hadamard matrix of dimension ![]() for k are given by the recursive formula:
for k are given by the recursive formula:
![]()
![]()
And in general
![]() (4)
(4)
This is also known as the Hadamard-ordered Walsh Hadamard matrix. Other orders, such as sequency order, dyadic order, and so on can be obtained by reordering the rows of the Hadamard matrix. Walsh Hadamard matrices 'in various orders have recently received growing concern due to the extensive application in engineering field.
To achieve the Fast Walsh Hadamard transform matrix, it is necessary to understand the “so-called Kronecker product”.
For any two matrices ![]() and
and![]() , the Kronecker Product of two matrices is defined as:
, the Kronecker Product of two matrices is defined as:
![]() (5)
(5)
In order to better understand the meaning of the Kronecker product, we define two new operators vec and mtx. The vec operator is to make all the columns of a matrix into a vector, and mtx is the inverse operator of vec that separates the vector into several equal-length vectors and forms a matrix.
According to “Kronecker product” theorem, Matrix ![]() can constructed by the Kronecker product formula:
can constructed by the Kronecker product formula:
![]() (6)
(6)
where ![]() and
and![]() , m and n are chosen to satisfy that m and n are divisible by p and q, respectively. Then matrix-vector multiplication can be computed by:
, m and n are chosen to satisfy that m and n are divisible by p and q, respectively. Then matrix-vector multiplication can be computed by:
![]() (7)
(7)
Detailed derivation process in [14]. Using the Kronecker product, the Formula (4) can rewritten as:
![]() (8)
(8)
For any two vector x with the length of![]() , denote
, denote![]() , where
, where ![]() and
and ![]() are the same size. The Hadamard-ordered Walsh Hadamard transform (
are the same size. The Hadamard-ordered Walsh Hadamard transform (![]() ) can be expressed as:
) can be expressed as:
![]() (9)
(9)
Due to the Basic KP theorem, it follows
![]() (10)
(10)
A implementation of the fast ![]() according to recursive Formula (10) would only have a computational complexity of
according to recursive Formula (10) would only have a computational complexity of![]() , but it is
, but it is ![]() of a general
of a general![]() . We can see that only additions and subtractions are involved while implementing the fast
. We can see that only additions and subtractions are involved while implementing the fast![]() .
.
Let ![]() represent the vectorized signal of the i-th wavelet sub-band. The corresponding measurement output vector can be written as:
represent the vectorized signal of the i-th wavelet sub-band. The corresponding measurement output vector can be written as:
![]() (11)
(11)
In each wavelet sub-band, we set the same sampling rate, so the number of measurements for each sub-band are the same.
3.2. Fusion
Multi-resolution wavelet decomposition has a noticeable advantage in the representation of a signal. In our fusion scheme, we take a single-level CDF-97 wavelet transform to decompose the original image into approximation coefficients and the detail coefficients. High frequency sub-band include the main energy of the original image and can considered to be sparse, but the scale coefficients low frequency sub-band is not considered to be sparse. So the low-frequency and high frequency coefficients multiplied with measurement matrix A together will destroyed the correlation between low-fre- quency approximate weight coefficient and the detail coefficients and lead to a poor reconstruction results. Hence, we preserving the low-pass wavelet coefficients and only measured the high-pass wavelet coefficients of the image. Then we fuse them with different fusion rules.
A) Fusion rule I
Let ![]() and
and![]() be the k-th (K = 1, 2, 3) low-frequency sub-images of image A and image B respectively. The fused approximation coefficient of the k-th low-frequency sub-images
be the k-th (K = 1, 2, 3) low-frequency sub-images of image A and image B respectively. The fused approximation coefficient of the k-th low-frequency sub-images ![]() can be formulated as:
can be formulated as:
![]() (12)
(12)
where ![]() and
and ![]() are the mean value of
are the mean value of ![]() and
and![]() . This strategy can keep the low-frequency better compare with general average weighted fusion strategy.
. This strategy can keep the low-frequency better compare with general average weighted fusion strategy.
B) Fusion rule I
Image structural similarity (SSIM) [15] is a kind of effective image quality evaluation index based on the hypothesis that the human visual perception is highly adapted for extracting structural information from a scene. Inspired by this, we use SSIM to extract the structure relation between two high-frequency sub-images measurement.
The structural similarity (SSIM) is designed by modeling any image distortion as the combination of structure comparison function![]() , luminance comparison function
, luminance comparison function![]() , contrast comparison function
, contrast comparison function![]() . SSIM is defined as:
. SSIM is defined as:
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
where ![]() and
and ![]() are the mean,
are the mean, ![]() ,
, ![]() and
and ![]() are the standard deviation and covariance, respectively. All of these is computed on the high-frequency sub-images measurement between image x and y. constant
are the standard deviation and covariance, respectively. All of these is computed on the high-frequency sub-images measurement between image x and y. constant![]() ,
, ![]() ,
, ![]() are included to avoid instability when denominator is very close to zero. Specifically,
are included to avoid instability when denominator is very close to zero. Specifically, ![]() ,
, ![]() where L is the dynamic range of the high-frequency sub-images measurement(maximum for two corresponding high frequency sub-band image measurement), and
where L is the dynamic range of the high-frequency sub-images measurement(maximum for two corresponding high frequency sub-band image measurement), and![]() ,
, ![]() is a small constant, in our experiments we set the parameter at 0.05,the other parameters of SSIM are all in accordance with Ref. [15].
is a small constant, in our experiments we set the parameter at 0.05,the other parameters of SSIM are all in accordance with Ref. [15].
For image fusion, it is useful to apply the SSIM locally rather than globally. In our experiments![]() ,
, ![]() and
and ![]() are computed within a local
are computed within a local ![]() square window, which moves pixel-by-pixel over the entire image. At each step, the local statistics and SSIM are calculated within the local window.
square window, which moves pixel-by-pixel over the entire image. At each step, the local statistics and SSIM are calculated within the local window.
At last, the mean SSIM (MSSIM) index to measure the similarity of two images defined as follows:
![]() (19)
(19)
where ![]() and
and![]() are the image information at the j-th local window, and M is the number of local windows of the image.
are the image information at the j-th local window, and M is the number of local windows of the image.
For the detail coefficients fusion, we let ![]() and
and ![]() be the measurement of the k-th (K = 1, 2, 3) high-frequency sub-images of image x and image y respectively. Then the fused high-frequency sub-image measurement
be the measurement of the k-th (K = 1, 2, 3) high-frequency sub-images of image x and image y respectively. Then the fused high-frequency sub-image measurement ![]() can be written as:
can be written as:
![]() (20)
(20)
where ![]() is the mean structural similarity index between two corresponding high frequency sub-band image measurement.
is the mean structural similarity index between two corresponding high frequency sub-band image measurement.
Consequently the fused high-frequency coefficient can be obtained through the TV minimization scheme based on augmented Lagrangian and alternating direction algorithms (TVAL3), see [14]. The specific steps of proposed method are summarized in Algorithm 1.
Algorithm 1. Image fusion in compressed sensing.
C) Algorithm
We recover the fused high-frequency coefficient from the fused high-frequency measurement using the TVAL3 algorithm [14].
4. Experimental Results and Performance Evaluation
In this section, three groups of test images are employed for the performance evaluation to illustrate the effectiveness of the proposed approach. Three pairs of source images including computed tomography (CT) and magnetic resonance imaging (MRI) images shown in Figure 1(a) and Figure 1(b), infrared and visual images, see Figure 2(a) and Figure 2(b), and optical multi-focus images, shown in Figure 3(a) and Figure 3(b). For more information about the images, refer to [16]. The high-frequency sampling rate is set at 0.2, and the total number of recover data is 40% of all the data. The sampling rate of other two methods is also set to 0.4 All experiments are implemented on an Intel Core(TM)2 Duo 2.33 GHz computer, and the simulation software is MATLAB 7.0.1.
In our experiment, We compare the proposed method with method in [11], which uses a “double-star” sampling pattern and a maximum absolute value selection fusion
rule (CS_MS) and [12], which uses a “star-shaped” sampling mode and a weighted average fusion rule based on Standard deviation (CS-SD). In medical image fusion, It's easy to see that the fusion results of the proposed method has a higher contrast and contains most of the details of the individual input images than CS_MS and CS-SD. Especially, the CS-SD has a low-contrast and contains noise compared with the original images. For the IR and visual images fusion, we can see that the results of our method also exhibit the best visual quality. Compared with our method, CS_MS scheme is not suitable for infrared and visual images fusion due to the distortion of brightness contrast and contain much strip noise. For the CS-SD, it losses contrast in the goals. In the last groups, our methods in the multifocus images fusion have a equal visual quality compared with CS-SD and is better than CS_MS.
For further comparison, several objective criteria are used to evaluate the fusion results. The first criterion is the average gradient (AG), which is commonly used to evaluate the clarity of image, the greater AG is, the sharper is the image. The next two criterion is the mutual information (MI) and edges keep degrees (![]() ), MI reflects the total amount of information that the fused image contains that of original image and
), MI reflects the total amount of information that the fused image contains that of original image and ![]() considers the amount of edge information transferred from the input images to the fused images. For the two criteria, the larger the value is, the better is the fusion result. Finally, we give the CPU running time for fusion and CS reconstruction, respectively.
considers the amount of edge information transferred from the input images to the fused images. For the two criteria, the larger the value is, the better is the fusion result. Finally, we give the CPU running time for fusion and CS reconstruction, respectively.
The performance evaluation of fusion results for three methods is shown in Table 1. It is obvious that our proposed method outperforms the other two methods in terms of MI and Q, which explain that the fused image of our method contains more detail and edge information compare with those of the other methods. It is consistent with the visual effect. Though the average gradient (AG) in the med image fusion is a little bigger than our method, its visual effect is far worse than ours. At last, it's worth noting that the CPU running time of our method for fusion and CS reconstruction is far less than the other two methods. In general, from the subjective visual comparison, and the objective index comparison, we can come to a conclusion that the proposed method gets a better performance than the other two methods.
![]()
Table 1. Performance evaluation of fusion results for our proposed method and other schemes.
5. Conclusions
In the paper, we put forward a kind of effective image fusion scheme based on compressive measurements. Compare with traditional method, we firstly take single layer wavelet transform for original image. Then, according to the characteristics of high frequency coefficients sparse, we only measured the high-pass wavelet coefficients with a low sampling rate. At last, we fuse low-frequency wavelet coefficient and high- frequency measurement with different fusion rules and recovery them with a new efficient TV minimization algorithm. Simulation results indicate that proposed scheme provides efficiency and promising fusion results. In addition, owing to the proposed scheme only needs incomplete measurements rather than acquiring all the samples of the whole image, the computational complexity significantly reduces. Moreover, because of using Fast Walsh Hadamard Transform, the CPU running time of our method for fusion and CS reconstruction is far less than other two methods.
CS image fusion is still in the stage of exploration, many problems remain to solve (e.g., the relationship between the original image and measurements and how to design the best fusion rule). Therefore the study of new and more advanced fusion rules matched with CS principle is another research topic in our future work.
Acknowledgements
This work was supported by the Gansu Academy of Sciences Youth Foundation under Grant 2015-QN-06. The associate editor coordinating the review of this manuscript and approving it for publication was Dr. Bo Zheng. The authors are with the Institute of sensing technology, Gansu Academy of Sciences (e-mail: glxygh@163.com; zhengboem@163.com).