1. Introduction
For today’s advances in bioinformatics, one of the main tasks is the prediction of protein structure in post-genome era of genomic research [1]. Improving the classification accuracy of the spatial structure of proteins not only helps to understand protein function but also helps to understand how proteins perform biological functions [2]. Depending on the difference of secondary structure alignment and topology fragment in protein sequence, Levitt and Chothia divided a protein sequence into four structural classes: all-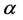
, all-
, 
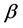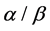and 
[3]. The current classification prediction algorithms are mostly concentrated on these four structural classes prediction.
Current methods for protein structure prediction are mainly focus on finding effective features of protein sequences and developing suitable machine learning algorithms. The former kind of research is mostly based on the amino acid composition [4] and pseudo-amino acid composition [5], which considered that similar sequences have similar protein structures. But the prediction results are easily affected by the sequence similarity. For example, the prediction accuracy of a high similarity dataset is 95% while the prediction accuracy of a low similarity dataset may be only 40% - 60%. Because the relationship between protein structures is most associated with protein secondary structure, someone proposed methods based on protein secondary structure and protein functional domain to predict protein structure [6]. Experiments show that for low similarity datasets this method also has a high prediction accuracy. After extracting effective features, you can use a variety of classification algorithms to classify the extracted feature vector, such as Neural networks [7], Support vector machines [8], Bayesian classification [9], rough set theory [10], Fuzzy classification [11], Logit Boost classifier [12], Information about the differences method [13], etc. Thus, an appropriate machine learning algorithm is very important to the prediction.
2. Materials and Methods
In this section, first, give the methods for extracting 16 features from the protein secondary structure to compose a 16-dimensional feature vector; second, change every protein sequence of 3 low similarity datasets (25PDB, 1189 and FC699 dataset) to a 16-dimensional feature vector; finally, classify the 16-dimensional feature vectors by GASVM algorithm.
2.1. Materials
To evaluate the proposed method and facilitate its comparison with other existing methods, 3 widely used benchmark datasets 25PDB [13], 1189 [9] and FC699 [16] with sequence similarity lower than 25%, 40% and 40% respectively were selected. The compositions of 3 datasets were shown in Table 1.
2.2. 16-Dimensional Feature Vector
Through PSIPRED [14] software, each amino acid residue of protein sequences can be mapped to one kind of the following three secondary structural elements: H (Helix), E (Strand), and C (Coil). In this paper, let SSS denote secondary structure sequence and
![]()
Table 1. Compositions of 3 datasets.
no-C-SSS denote the sequence that was removed coil structure from secondary structure sequence. Let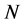 
and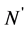 
denote the length of SSS and the length of no-C-SSS respectively. For convenience, the 16-dimensional feature vector which is extracted from protein secondary structure is denoted by
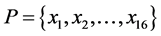. The method to extract the feature vector will be described in more detail.
1) The first two features represent the proportion of H and E in SSS respectively, which have been proved significantly helpful in improving accuracy of protein structural classes[15], The features are as follows:
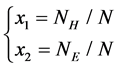
where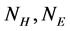 
is the number of 
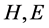in the SSS respectively. Since 
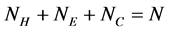(where 
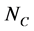is the number of 
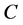in the SSS), we only need to extract 
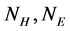two features to represent the SSS.
2) To classify the protein structures, the maximum length and the average length of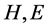 
and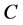 
segments (the successive same letter) are also important factors. Six features are described as follows:
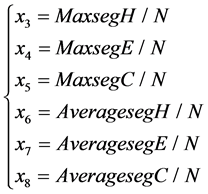
The![]()
, ![]()
and ![]()
are the maximum length of segment and ![]()
and ![]()
in SSS respectively.
3) The more segments whose length reaches a certain value, the more likely to determine the structure of a protein. We respectively selected the segment ![]()
whose length is greater than 5 and the segment ![]()
whose length is greater than 3 as features of protein secondary structure [20]. In order to represent the structure more accurately, we also extracted segments position information in SSS. That can be defined as follows:
![]()
where, ![]()
is the number of segment![]()
, ![]()
is the number of segment![]()
, ![]()
is the position of ![]()
![]()
in the protein secondary structure sequence.
4) While proteins in the ![]()
and ![]()
classes contain both ![]()
-helices and ![]()
-strands, there is a decided difference in the distribution of them. ![]()
-helices and ![]()
-strands are usually separated in the ![]()
class, but are usually interspersed in the ![]()
class [20]. Therefore, it is necessary to extract features from the no-C- SSS. In this paper we extract 5 features from no-C-SSS that only have H and E segments first time. The features are defined as follows:
![]()
![]()
is the number of two adjacent ![]()
segments in no-C-SSS, ![]()
is the number of ![]()
segment-![]()
segment, ![]()
is the number of ![]()
segment-![]()
segment, ![]()
is the number of ![]()
segment-![]()
segment-![]()
segment, ![]()
is the number of ![]()
segment-![]()
segment-![]()
segment-![]()
segment.
2.3. Construction of Classification Algorithm
2.3.1. Support Vector Machine
There are many algorithms to solve the protein multi-classification problem, such as neural net-work classification, support vector machine (SVM), Bayesian classification and so on. In this paper, support vector machine is selected for protein classification. The basic idea of SVM is map the data to a high dimensional space, and then find the data partition hyper plane in the high dimensional space. SVM has been widely used in protein secondary structure classification for its high prediction accuracy [17]. In this paper, we use “one-to-one” multi-classification method, and then combine 6 two-clas- sifiers to achieve multi-classification. Compared with other kernel function, the radial basis kernel function is better when deal with nonlinear problem [18]. So we select the radial basis kernel function ![]()
as kernel function.
2.3.2. GASVM Algorithm
Genetic algorithm (GA) is a method based on the principle of natural selection and genetic optimization search. It includes several steps, such as chromosome coding, population initialization, fitness function calculating, basic genetic operation and so on. Here, GASVM algorithm is proposed to optimize the coefficients of these 16 features in the classification. The classification accuracy of SVM is regarded as the fitness function value of GASVM algorithm. The steps of GASVM algorithm are described as follows:
1) Let the coefficient vector be![]()
. Randomly generate 16 initial coefficients between [0,1] and code every chromosome with binary coding respectively. Then 200 chromosomes initialized compose the initial population.
2) The new feature vector ![]()
is the dot product of coefficient vector ![]()
and feature vector![]()
.
3) Calculate the new feature vector ![]()
of each protein sequence. Classify the feature vectors by SVM of 2.3.1, The bigger fitness value of the corresponding chromosome is in the algorithm, the greater the probability of chromosome survival is. To improve the classification accuracy, the classification accuracy of SVM is regarded as the fitness function value.
4) The first 160 individuals with big fitness function values are selected as parents in the next generation. In order to obtain the global optimum solution and improve the convergence rate, sorting selection method is adopted, the top 80% chromosomes with higher fitness from population are selected and copied into the mating pool.
5) A new generation is produced by the genetic and crossover operation of paternal generation chromosomes. The multi-point crossover is adopted.
6) In the new generation, 40 population samples are selected randomly, and then mutation is performed. It means the values of certain genes of a chromosome are replaced with other values to generate a new individual. Here, 5% of the chromosomes are mutated by point mutation method.
7) Repeat steps (2) to (6) until the fitness function values satisfy the requirement or the maximum number of cycles is reached.
3. Results and Discussion
The protein sequences in 25PDB, 1189, FC699 3 datasets were classified by GASVM algorithm and 10-fold cross-validation was used. The classification accuracy can be seen in Table 2, the overall accuracy of the 25PDB, 1189, FC699 dataset is 83.32%, 85.44% and 93.36% respectively, the accuracy of all-![]()
, all-![]()
, ![]()
and ![]()
bigger than 92.35%, 86.69%, 81.02% and 73.33% respectively. Figure 1 shows the optimal coefficients, the differences among 16 coefficients are obvious.
![]()
Table 2. The results for the 3 datasets with 10-fold cross-validation.
![]()
Figure 1. The optimal coefficients of 3 datasets.
4. Comparison with Other Methods
The SCPRED, MODAS and RKS-PPSC methods are widely accepted in protein structure classification and the 25PDB, 1189, FC699 3 datasets are adopted to validate the effects. Here, the results of GASVM algorithm were compared with SCPRED, MODAS, RKS-PPSC and reference [20] (see Table 3). The data in Table 3 show that the overall accuracies obtained by our method are higher than other methods on 25PDB, 1189 and FC699 datasets, which increase 0.42%, 1.90% and 1.59% respectively.
Our method obtains the highest prediction accuracies for the classes among all the tested methods on 3 datasets. As for the class, the accuracy is 83.53% on 25PDB dataset and 86.69% on 1189 dataset, which is 0.17% and 0.41% lower than that of the famous MODAS method [21] respectively, but is 3.43% higher than SCPRED [17] and 2.29% higher than kongs’ method [20]. About the class, the accuracy is 81.02% on 25PDB dataset, which is 4.78% lower than that of the RKS-PPSC [22], but is 7.02% higher than SCPRED [17]; the accuracy is 87.11% on 1189dataset, which is 2.49% lower than SCPRED, but is 4.51% higher than RKS-PPSC. It is also noticed that the significant improvement is made in particular for the class, which is the difficult class to predict.
5. Conclusion
In the paper, the importance of the weights of different features in protein structure classification are considered, so GASVM algorithm is proposed to optimize the coeffi-
![]()
Table 3. The comparison of different methods.
cients of these 16 features in the classification. Finally, 10-fold cross-validation is used to classify the protein structures of3 low similarity datasets (25PDB, 1189, FC699) and experimental results show that the overall classification accuracy of the new method is better than other methods. GASVM algorithm is very effective in protein structure classification. Weights of different features are considered is very necessary.
Acknowledgements
The authors would like to thank all of the researchers who made publicly available data used in this study and thank the National Natural Science Foundation of China (No: 61303145) for the support to this work.