Nano-Contact Problem with Surface Effects on Triangle Distribution Loading ()
1. Introduction
Nowadays, nanometer material and technology have been widely used in industrial and engineering fields. Many new nano-materials have been developed by utilizing the fact that materials begin to exhibit unique mechanical properties at nano-scale, which significantly differ from those at larger scale.
Nano-indention tests have been widely used to measure such mechanical properties of materials. For micro-nano solids with large surface-to-bulk ratio the significance of surfaces is likely to be important. Form the viewpoint of continuum mechanics, this difference can be described by such concepts as surface effects [1] . This is especially true for nano-scale materials or structures. In such cases, the surface tension and the surface elasticity play a critical role and thus have been adding its appeal to many researchers. For example, Miller and Shenoy [2] probed the size-dependent elastic properties of nano-plates and beams. Hang et al. [3] explained the size dependent phenomenon by the strain gradient continuum theory. Dingreville et al. [4] investigated the surface free energy and its effect on elastic behavior of the nano-sized particles, wires, and films. Yang [5] studied the size-dependent effective modulus of spherical nano- cavities at dilute concentrations. Gao et al. [6] built a simple model to describe the influence of surface stress on the nanoscale adhesive contact. There are a lot of work regarding the surface/interface energy effects on the nanostructures and solids, and we can only include a small part of them here. For more recent developments in this field, the readers can refer to a review article by Wang et al. [7] .
To study the mechanical behavior of nano-materials, the most celebrated continuum-based surface/interface model was first established by Gurtin, Murdoch and coworkers [8] [9] [10] , which known as the theory of surface elasticity. In the study of nano-scale problems, all material constants appearing in that constitutive model were commonly calibrated with data obtained from either experimental measurements [11] or atomistic simulations [2] [12] . Therefore, the surface effect has been widely adopted to investigate the mechanical phenomena at nano-scale. Cammarata et al. [13] considered the size-dependent deformation in thin film with surface effects. Gao et al. [14] developed a finite-element method to account for the effect of surface elasticity. Wang et al. [15] studied to a half-plane subjected to normal pressures with surface tension. Zhao and Rajapakse [16] proposed a continuum-based model to study the influence of surface stresses on mechanical responses of an elastic half-space compressed by an axisymmetric, rigid, frictionless nano-indentor. Long and Wang [17] studied the effect of the residual surface stress on the two dimensional Hertz contact problem, and later Long et al. [18] generalized their work to the three dimensional case. Wang [19] derived the general analytical solution of nano-contact problem with surface effects by using the complex variable function method. Gao et al. [20] [21] derived the influence of the surface stress on the JKR adhesive contact, which is investigated by employing the non-classical Boussinesq fundamental solutions. In this paper, Fourier integral transform method is used to solve the non-classical boundary value problems with surface effects.
2. Problem Description
Now we consider a material occupying the upper half-plane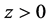
, we refer to a Cartesian coordinate system (o-xyz), as shown in Figure 1, where the x axis is along the surface and the z axis perpendicular to the surface. It is assumed that the material is subjected to triangle distribution force 
and 
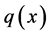over the region
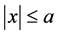. While the normal and shear force form zero (
and
) uniformly increased to maximum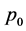 
and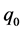 
at the point O. The plane-strain conditions are assumed to
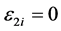, and
![]()
Figure 1. Schematic of contact problem under triangle distribution loads.
the contact is assumed to be frictionless.
The problem statement is to determine the triangle distribution force exerted by the elastic field (e.g., displacement and stresses) with the half-plane for the influence of surface effects.
3. Basic Equations of Surface Elasticity and General Solutions
In surface elasticity theory, the equilibrium and constitutive equations in the bulk of material are the same as those in classical elastic theory, but the presence of surface stresses gives rise to a non-classical boundary condition.
3.1. Basic Equations
In the absence of body force, the equilibrium equations, constitutive law, and geometry relations in the bulk are as follows
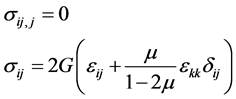(1)
where G and 
are the shear modulus and Poisson’s ratio of the bulk material,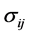 
and 
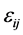are the stress tensor and strain tensor in the bulk material, respectively.
The strain tensor is related to the displacement vector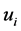 
by
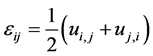(2)
On the surface, the generalized Young-Laplace equation [22] , surface constitutive relation and strain-displacement relationship can be expressed as
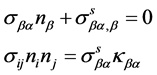(3)
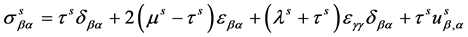(4)
where ![]()
denotes the normal to the surface, ![]()
the curvature tensor of the surface, ![]()
is the ![]()
surface stress tensor on the surface, ![]()
is the stress tensor in the elastic material, and ![]()
is the ![]()
surface strain tensor which is equal to the tangential components of the strain tensor of the elastic material on the surface, ![]()
is the residual surface tension under unstrained conditions, ![]()
and ![]()
are surface Lamé constants which can be determined by atom simulations or experiments [2] .
3.2. General Solutions
Based on previous work by Wang [15] and Wang [23] , Fourier integral transformation method is adopted to solve the stress and displacement components by
![]()
(5)
where A and B are generally functions of ![]()
as yet to be determined by boundary conditions.
4. Elastic Solution under Normal Triangle Distribution Force
As a particular example, let us consider the effect of a normal triangle distribution force ![]()
over the region![]()
, and the normal force form zero (![]()
and![]()
) uniformly increased to maximum ![]()
(O), while remainder of the boundary ![]()
being unstressed as shown in Figure 1.
![]()
![]()
(6)
Due to the surface tension mostly influences the normal stress [20] . Therefore, we keep only the first term in Equation (4). Then, the surface stresses are given by
![]()
(7)
On the surface, the boundary conditions (3) can be written by
![]()
(8)
Substituting Equation (8) into Equation (5), one obtains
![]()
(9)
Due to deformation the radius of curvature of the surface is given by
![]()
(10)
By substituting Equations (9) and (10) into the surface condition Equation (8), ![]()
is determined by
![]()
(11)
where
![]()
(12)
![]()
(13)
where s is a length parameter depending on the surface property and material elastic constants. It should be pointed out that this parameter indicates the thickness size of the zone where the surface effect is significant, and plays a critical role in the surface elasticity. For metals, s is estimated on the order of nanometers.
Therefore ![]()
is given by
![]()
(14)
Substituting Equation (14) into Equation (5), the stresses component and displaces component are obtained as
![]()
(15)
It is seen, when![]()
, that is, the surface influence is ignored in Equation (15), the stresses of the half-plane are consistent with those in the classical elastic contact results which is the same result [23] , respectively.
![]()
(16)
where
![]()
.
On the contact surface (![]()
), the normal stress is given by
![]()
(17)
According to the Saint-Venant’s Principle, we assume that the normal displacement is w specified to be zero at a distance ![]()
on the contact surface, that is,![]()
, the displacement on the surface is derived as
![]()
(18)
Assuming that the origin has no displacement in the x direction, that is, ![]()
one obtains
![]()
(19)
As show in Figure 2, the results indicated that the normal stress ![]()
is a smooth distribution when the surface tension is considered by at the loading boundary (![]()
), However, it is just the reverse with classical results that is the surface tension is ignored (s/a = 0). In addition, the actual normal stress ![]()
is smaller than the classical value in the loading zone and is larger outside of the zone.
Due to the different surface tension value, the horizontal displacement is displayed in Figure 3, where we set![]()
, and![]()
. It is seen that the horizontal displacement is continuous everywhere on the deformed surface. However, the classical elasticity theory predicted unreasonably that the horizontal displacement is discontinuously at the load boundary![]()
, as seen from the curve of s/a = 0. The indent depth is plotted in Figure 4 with![]()
, which also shows that the slope of the deformed surface is continuous everywhere. It is also found the indent depth decreases with the increase of surface tension.
5. Elastic Solution under Tangential Triangle Distribution Force
Now, let us consider the effect of a tangential triangle distribution force ![]()
over the region![]()
, while the shears force form zero (![]()
and![]()
) uniformly increased to maximum ![]()
at the point O, while remainder of the boundary ![]()
being unstressed as shown in Figure 1.
![]()
Figure 2. The distribution of contact normal stress ![]()
under normal triangle distribution load.
![]()
Figure 3. The distribution of surface displacement u under normal triangle distribution load.
At this moment, the boundary conditions (3) on the contact surface (![]()
) are simplified to
![]()
Figure 4. The distribution of surface indentation w under normal triangle distribution load.
![]()
(20)
where ![]()
is the tangential triangle distribution force applied on the materials surface, and ![]()
is a surface constant.
![]()
![]()
(21)
Substituting Equation (21) into Equation (20), one can be obtained
![]()
(22)
where
![]()
(23)
![]()
(24)
where b is a length parameter depending on the material surface property. It should be pointed out that this parameter plays a critical role in the surface elasticity.
Substituting Equation (24) into the surface condition Equations (12) and (13), the solution of stresses and displaces under pure shear load were obtained
![]()
(25)
Substituting Equation (24) into Equations (22), one obtains
![]()
(26)
Therefore ![]()
is given by
![]()
(27)
Substituting Equation (27) into Equations (25), the stresses component and displaces component are obtained as
![]()
(28)
It is seen, when![]()
, that is, the surface influence is ignored in Equation (28), the stresses and displacements of the half-plane are consistent with those in the classical elastic results [24] , respectively.
![]()
(29)
On the contact surface![]()
, the stresses is given by
![]()
(30)
Based on the previous assumption, ![]()
, the displacement on the surface component is derived as
![]()
(31)
It is instructive to examine the influence of the surface elasticity on the stresses and displacements of the contact surface and compare them with those in classical contact problem. Figure 5 and Figure 6 show the distribution of the stresses ![]()
and ![]()
on the contact surface, where the solution of b/a = 0 is consistent with the classical elastic result.
It can be seen from Figure 7 that the normal stress ![]()
transits continuously across the loading boundary![]()
, which is increasing monotonically with respect to x in the loading region (![]()
), and the inverse is observed outside the loading region (![]()
). It means that the analytical expressions can give approximate results in the region that is far from the loading boundary. It is also found Figure 5 that shear stress changes smoothly across the loading boundary![]()
, which is different from a
![]()
Figure 5. The distribution of the shear stress ![]()
under tangential triangle distribution load.
![]()
Figure 6. The distribution of surface displacement u under tangential triangle distribution load.
![]()
Figure 7. The distribution of the normal stress ![]()
under tangential triangle distribution load.
singularity predicted by classical elasticity.
Due to the different surface elasticity value, the horizontal displacement is displayed in Figure 6, where we set![]()
, and![]()
. It is seen that the slope of
![]()
Figure 8. The distribution of surface indentation w under tangential triangle distribution load.
the deformed surface for a > 0 is continuous everywhere. It is also found the horizontal displacement decreases with the increase of surface elasticity. The indent depth is plotted in Figure 8 with![]()
, which also shows that the normal displacement is continuous everywhere on the deformed surface. In addition, the indent depth decreases continuously with the increase of surface elasticity.
6. Conclusion
In this paper, we consider the two-dimensional contact problem in the light of surface elasticity theory. Fourier integral transform method is adopted solving general analytical solution. For two particular loading cases of triangle distribution forces, the results are analyzed in detail and compared with the classical linear elastic solutions. A series of theoretical and numerical results show that the influences of the surface tension and the surface elasticity on the stresses and displacements are not always equal. It is found that the surface elasticity theory illuminates some interesting characteristics of contact problems at nano-scale, which are distinctly different from the classical solutions of elasticity without surface effects. Therefore, the influence of surface effects should be considered for nano-contact problems.